Towards a formalization of model conformance in

Model Driven Engineering

Thanh-Hà Pham

1,2

, Mariano Belaunde

Jean Bézivin

France Télécom R&D, 2 avenue Pierre Marzin, 22300 Lannion Cedex, France

ATLAS Group, INRIA&LINA, University of Nantes, France

Abstract. The principle of “everything is an object” basically supported by two

fundamental relationships inheritance and instantiation has helped much in

driving the object technology in the direction of simplicity, generality and

power of integration. Similarly in the Model Driven Engineering (MDE) today,

the basic principle that “everything is a model” has many interesting properties.

The two relations representation and conformance

are suggested [2] to be the

two basic relations in the MDE. This paper tends to support this ideas by

investigating some concrete examples of the conformance relation concerning

three technological spaces (TS) [10]: Abstract/Concrete Syntax TS, XML TS

and Object-Oriented Modeling (OOM) TS. To go further in this direction we

try to formalize this relation in the OOM TS by using the category theory – a

very young and abstract but powerful branch of mathematics. The OCL

language is (partially) reused in this scheme to provide a potentially useful

environment supporting MDE in a very general way.

1 Introduction

Model Driven Engineering (MDE) today does not limit itself to the OOM

Technological Space (TS) but many other TSs such as AS TS, XML TS ... [10]. This

means explicitly that its principles must be very general and not only restricted to

OOM TS. Today, the principle « Everything is a model » as suggested by many

authors such as [3] becomes the main principle of the MDE similarly to the principle

« Everything is an object » in object technology. Conformance is one of the

fundamental relations supporting this principle in MDE. This paper investigates the

conformance relation in some well-known Technological Spaces such as

Abstract/Concrete Syntax, XML and OOM technological spaces.

The paper is organized as follow: section 1 presents t

he context of our work; section 2

presents some ideas about the notion of conformance in several well-known TSs;

section 3 presents a formalization of the conformance relation in the OOM TS using

category theory and the OCL language. The practical usage of this formalization will

be discussed in the section 4. Some related works are briefly introduced in the section

5. Some conclusions will be provided in the section 6.

Pham T., Belaunde M. and Bézivin J. (2005).

Towards a formalization of model conformance in Model Driven Engineering.

In Proceedings of the Joint Workshop on Web Services and Model-Driven Enterprise Information Systems, pages 107-116

DOI: 10.5220/0002570601070116

 SciTePress

2 Conformance in some Technological Spaces

We begin our discussion with a simple example coming from Regular Expression. It

is not difficult to see that there is a mapping from a string S = acccd to a regular

expression E = a(b|c*)d? when the string S matches the expression E. This mapping is

illustrated in the Fig.1.

a (b | c*) d?

a c c c d

Fig. 1. A very simple form of conformance – a string matches a regular expression

The regular expression E defines characters that may appear in a string conforming to

E: {a,b,c,d} and how these characters are structured using several constructions:

– alternation with a vertical bar such as b | c specify the choice of b or c.

– quantification with a quantifier (+,?,*) that following a character specifies how

often that character is allowed to occur.

– grouping with brackets to define the scope and precedence of the other operators.

If the guiding principle of the MDE:

“Everything is a model” [P0]

is accepted, we have the following two models: the string S and its definition E (is

also a string) with their characters as model elements. It can be said that S is defined

by E or S conforms to E.

“A model conforms to its definition, this definition is also a model called meta-model

of the first one” [P1]

From our first observation, we propose the following principle:

“Every element of a model finds an unique definition in a meta-model that the model

conforms to” [P2]

We have also the following comments:

– The order of elements in S must respect to the order of elements defined in E. [C1]

– The group of elements in S must respect to the group definition in E. [C2]

– The number of occurrences of elements in S must respect to quantification

definitions in E. [C3]

Now we move to an illustrative example in the Abstract/Concrete Syntax TS. Let’s

consider a well-known HelloWorld program written in the Pascal programming

language. This program is considered to be a syntactically correct with respect to the

grammar of the Pascal programming language. In this example, the HelloWorld

program is a model and the grammar of the Pascal programming language is the

meta-model defining the former. The principle [P2] is applicable in this case and is

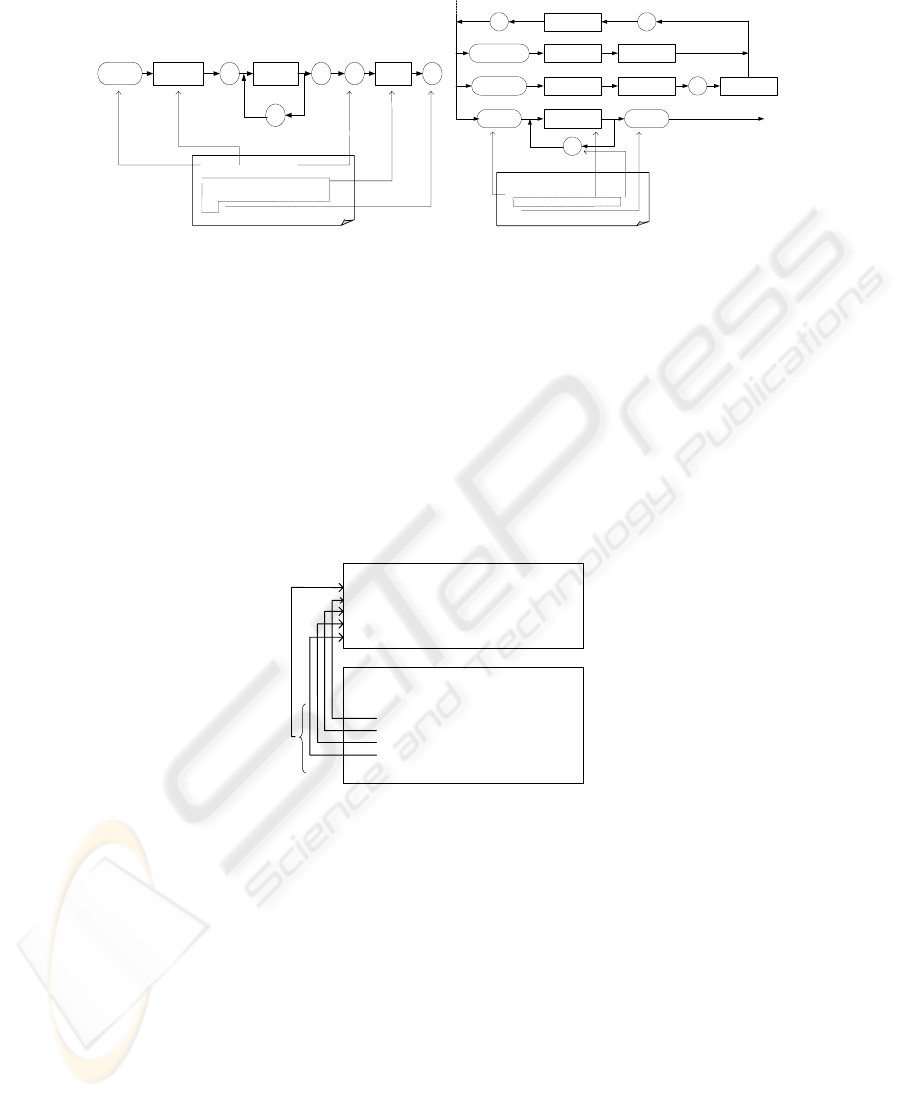
illustrated in the Fig.2. A part of the grammar is represented in the flowchart form

extracted from [9]. Every symbol of this program finds a unique definition in the

grammar. The three comments [C1, C2, C3] are also correct in this case.

108

program HelloWorld;

begin

writeln('Hello World');

end.

program

PROGRAM

identifier

(

identifier

)

;

block

;

BEGIN END

statement

;

; block ;

PROCEDURE

FUNCTION

identifier parameter list : type identifier

identifier parameter list

block

program HelloWorld;

begin

writeln('Hello World');

end.

Fig. 2. A Pascal program conforms to the grammar of the Pascal programming language

In the XML TS, we find the following definition [6]: « An XML document is valid if it

has an associated document type declaration and if the document complies with the

constraints expressed in it ». This means explicitly that a valid XML document must

conform to a DTD. DTDs specify two kinds of constraints as classified in [5]:

structural constraints given by element declaration rules and attribute constraints

given by attribute declaration rules. Also following [5], « the structural constraints of

DTD are abstracted as extended context free grammars, that is, context free

grammars where the right hand side of each production contains a regular

expression. An XML document is valid with respect to the structural constraints of a

DTD if its abstraction as a tree represents a derivation tree of the extended CFG

corresponding to that DTD ». Attribute constraints deal with the values of attribute

nodes while structural constraints deal with the labels of nodes in the XML tree.

<?xml version="1.0"?>

<!ELEMENT message (from,to,subject,body)>

<!ELEMENT from (#PCDATA)>

<!ELEMENT to (#PCDATA)>

<!ELEMENT subject (#PCDATA)>

<!ELEMENT body (#PCDATA)>

<?xml version="1.0"?>

<!DOCTYPE message SYSTEM "message.dtd">

<note>

<to>Mariano</to>

<subject>Work completed</subject>

</note>

Fig. 3. An XML document conforms to a DTD.

Let’s consider an example that illustrates the relation between an XML document and

a DTD. In this case, the model is the XML document and the meta-model defining

this model is the DTD. The XML document has (element and attribute) nodes as its

elements. The principle [P2] and the three comments [C1, C2, C3] are also applicable

in this case.

We have analyzed the conformance relation in the case of regular expression,

Abstract/Concrete syntax and XML. The principle [P2] is also applicable in Object-

Oriented modeling.

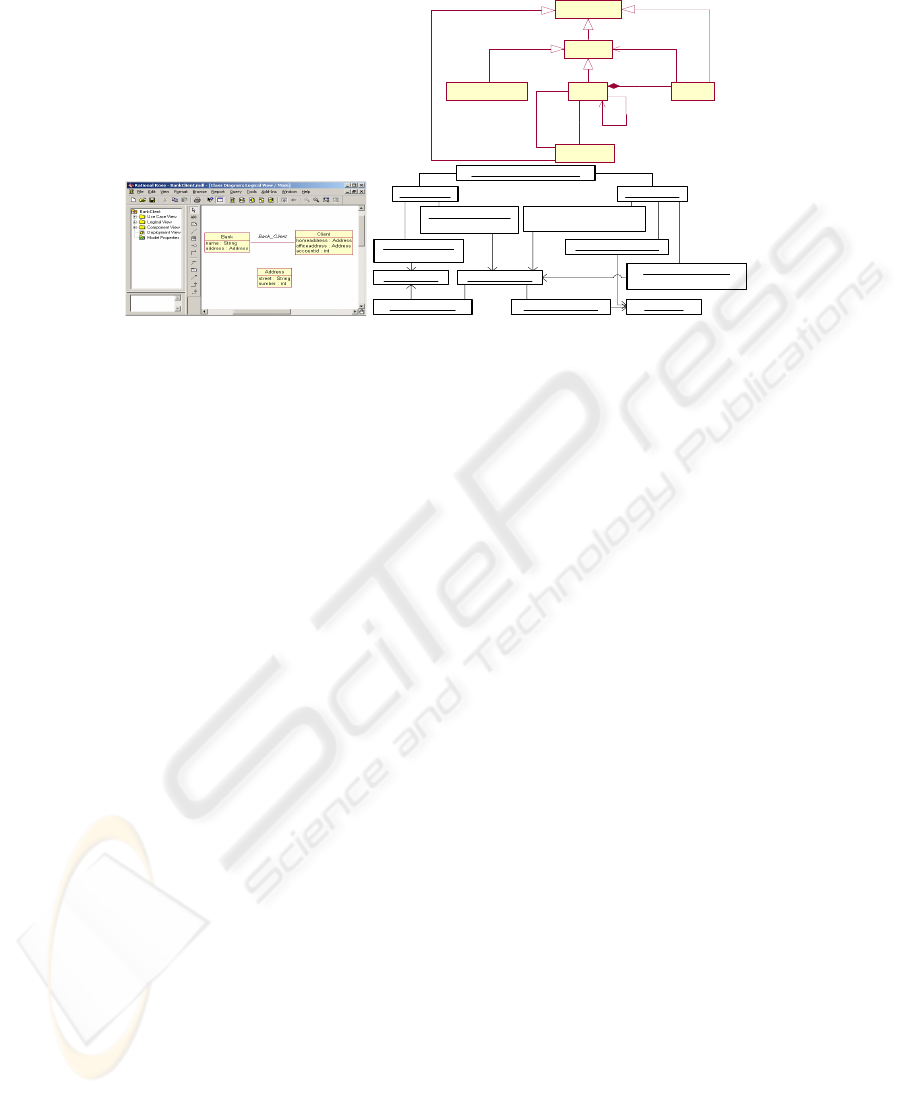
In the left of the Fig.4 is an UML diagram represented in a case tool such as Rose.

This model is an instance-of of the UML meta-model as simplified in Fig.4. Every

elements of this model finds its unique definition in the meta-model.

109

ModelElem ent

PrimitiveDataType

Classifier

Attribute

+type

Association

Class

+super

0..1

+attribute

+source

+forward

+reverse

+destination

Bank:Class

Bank_Client:Association

Client:Cla ss

String:Class

bname:Attribute

name = "name"

baddress:Attribute

name="address"

chaddress:Attribute

name="homeaddress"

coaddress:Attribute

name ="officeaddress"

accountid:A ttribute

Address:Class

street:Attribu te

number:Attribute

int:C lass

Class::allParents(): Set(Class);

allParents = self.super->union(self.super->collect(p | p.allParents())

context Class

inv: not self.allPare nts()->includ es(self)

Fig. 4. An illustrative example: a model UML conforms to its meta-model

An UML model conforms to the UML meta-model must also satisfied all the well-

formedness rules defined with the meta-model. The multiplicity in the meta-model

can also be expressed as constraints associated to the meta-model [16]. Furthermore,

we have the following principle:

– Every link in the model finds a unique definition in the meta-model. [P3]

This principle is so important as the [P2] principle for a model UML and also for the

conformance relation between a model and a meta-model defining it in meta-

modeling. These two principles [P2, P3] are also applicable in the “strict meta-

modeling” approach in which the OMG’s MOF is an example: “Every element of an

level model is an instance_of exactly one element of an M

n+1

level model” [1].

3 A formalization of the conformance relation in the OOM TS

In a very general way, a model can be viewed as containing:

– A set of model elements (character in a string or regular expression, symbols and

terminals in a grammar, element or attribute nodes in XML, model elements in

modeling)

– Some of those elements are associated to some sorts of literal (integer, real,

string....)

– A set of links that associates elements (link is directed). Those links forms a

navigation network among model elements.

– To make sense, each model must be associated with a meta-model defining it.

– Every model element finds its unique definition in the meta-model.

– Every model link finds its unique definition in the meta-model.

The fact that there is a mapping from a model (the defined artifact) and its meta-

model (the defining artifact) is one of the necessary conditions for the model to

conform to its meta-model. This mapping includes model elements mapping and

model links mapping and is then a structural mapping. Together with this structural

mapping the model must satisfy constraints associated to the meta-model. Those

110

constraints can be evaluated based on structural mapping and literal values associated

to model elements.

Before taking into details of the formalization, we put some words about the category

theory. Category theory originally arose in mathematics out of the need of formalism

to describe the passage from one type of mathematical structure to another [7].

Category theory has been used in diverse branches of software engineering and

computer science as pointed out by Goguen [8], in object-oriented software evolution

[11] and recently the formalization of UML [14] and MOF [4] etc. In category theory

there are structures called categories that contain objects and morphisms. Those

morphisms can be composed and the composition of morphisms is associative.

Functor is a structure-preserving mapping between two categories. Definitions of

category, functor and other notion of category theory can be found at [15], [7]. A

computational aspect of category theory can be found in [12].

The next topic is the proposed formalization of the conformance relation between a

model and its meta-model in the OOM TS. The OOM TS bases on OMG’s

technology (MOF, UML, QVT...), which is originally based on object models.

Adapted from [13], an object model is a tuple

µ=(CLASS,ATT

,OP

,ASSOC,associates,roles,multiplicities,<,

PRIMITIVETYPE)

such that

i. CLASS is a set of classes.

ii. ATT

is a set of operation signatures for functions mapping an object of

class c to an associated attribute value.

iii. OP

is a set of signatures for user-defined operations of a class c.

iv. ASSOC is a set of association names.

a. associates is a function mapping each association name to a list

of participating classes.

b. roles is a function assigning each end of an association a role

name.

c. multiplicities is a function assigning each end of an

association a multiplicity specification.

v. < is a partial order on CLASS reflecting the generalization hierarchy of

classes.

vi. PRIMITIVETYPE is a set of primitive data types used in the object

model = {STRING, INTEGER, REAL }.

In our formalization, model navigation plays an important role. We proposed the

concept of navigation morphism which is represented by a tuple

nav = (e

, L, E

)

such that

i. e

is the model element that is the source of the navigation morphism

ii. L is a sequence of navigation label

iii.

is a sequence of elements that is orderly located in the navigation

from the source element e

to the target element. The last element of

this sequence is the target of the navigation morphism.

Now, from every object model µ, there is a derived category C

111

= (Ob

,Mor

,dom,cod,id,composition)

such that

i. Ob

= CLASS ∪ PRIMITIVETYPE

ii. PRIMITIVETYPE is the set of primitive types used in the object

model

iii. Mor

= Mor ∪ Mor

C1 C2

iv. Mor

is the set of all navigation morphisms

, [role name],[e

])

representing a navigation from e

to e

∈ CLASS)

through the

“role name” role. Mor

can be calculated from CLASS, ASSOC,

associates and roles.

v. Mor

is the set of all navigation morphisms

, [attribute name],[e

])

representing a navigation from e

∈ CLASS)

to e

∈

PRIMIVITES) through the “attribute name” attribute. Mor

can be calculated from CLASS, ATT

, PRIMITIVETYPE.

vi. dom: Mor

→ Ob

is a function that takes a navigation morphism as

argument and gives the source of that navigation morphism as result.

This function can be calculated from CLASS, ATT

, ASSOC,

associates, roles and <.

vii. cod: Mor

→ Ob

is a function that takes a navigation morphism as

argument and gives the target of that navigation morphism as result.

This function can be calculated from CLASS, ATT

, ASSOC,

associates, roles and <.

viii. id is an identity function that takes a model element e as its argument

and give a navigation morphism (e,[],[e]) as result. i.e this

function returns a navigation morphism from the element e to itself

(there is no navigation label)

ix. composition is a function that takes two navigation morphisms

nmor1 = (e

) and nmor2 = (e

) as its

arguments and give a composite navigation morphism

nmor=(e

concat

concat E

)

when cod(nmor1)=dom(nmor2)

Once the model µ is promoted as a meta-model (M

level), any model of this meta-

model can be represented by a category :

model

= (Ob

,Mor

,dom,cod,id,composition)

such that

i. Ob

= OBJECT ∪ LITERAL

ii. OBJECT is the set of objects in the selected model

iii. LITERAL is the set of objects associated to a primitive value used in

the selected model

iv. Mor

= Mor

∪ Mor

v. Mor

is the set of all navigation morphisms

, [role name],[e

])

representing a navigation from e

to e

∈ OBJECT)

through the

“role name” role. Mor

can be calculated from the selected model.

112

vi. Mor

is the set of all navigation morphisms

, [attribute name],[e

])

representing a navigation from e

∈ OBJECT)

to e

∈

LITERAL) through the “attribute name” attribute. Mor

can be

calculated from the selected model.

vii. dom: Mor

→ Ob

is a function that takes a navigation morphism as

argument and gives the source of that navigation morphism as result.

This function can be calculated from the selected model.

viii. cod: Mor

→ Ob

is a function that takes a navigation morphism as

argument and gives the target of that navigation morphism as result.

This function can be calculated from the selected model.

ix. id is an identity function that takes a model element e as its argument

and give a navigation morphism (e,[],[e]) as result. i.e this

function returns a navigation morphism from the element e to itself

(there is no navigation label)

x. composition is a function that takes two navigation morphisms

nmor1 = (e

) and nmor2 = (e

) as its

arguments and give a composite navigation morphism

nmor=(e

concat

concat E

)

when cod(nmor1)=dom(nmor2)

An example: BankClient model conforms to SimpleUML model

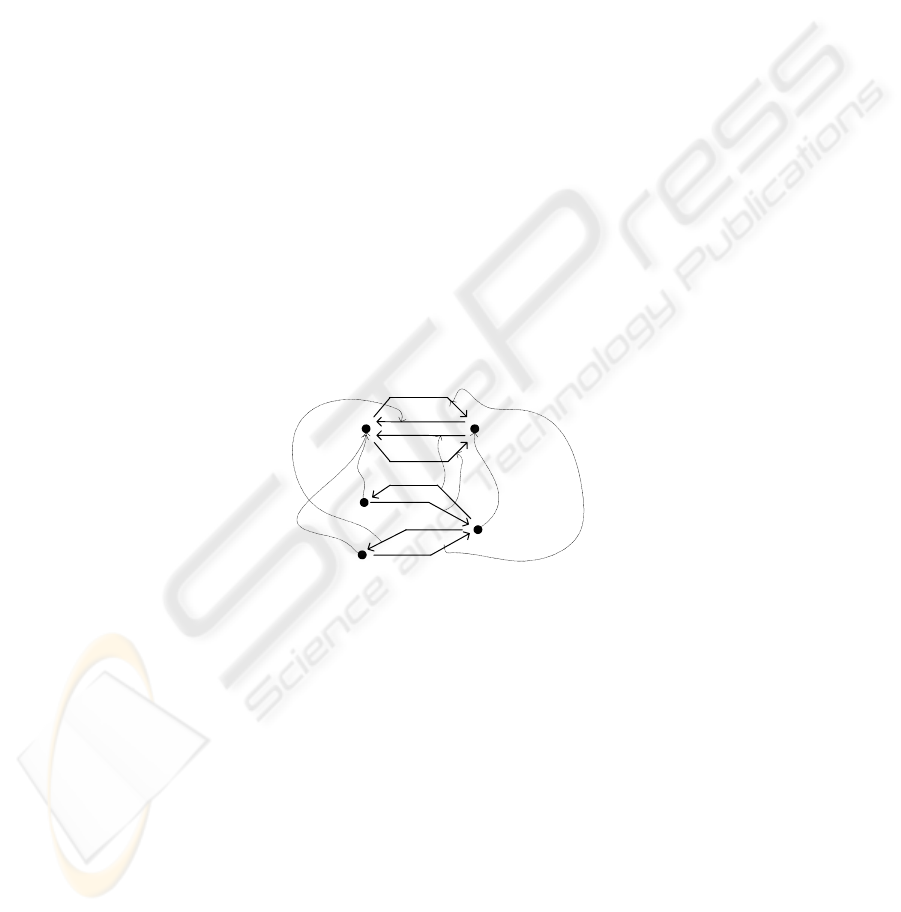
The simplified meta-model UML and the Bank_Client model (Fig.4) are illustrated

partially in the categorical form in the Fig. 5. Model elements and model links of

these two models is provided in the Table.1.

Class

Association

reverse

forward

Bank

Client

Bank_Client

source

forward

reverse

destination

Fig. 5. A partial view of mapping from BankClient (model) to SimpleUML (meta-model)

The mapping from Bank_Client model to SimpleUML model illustrated in the

Table.2 can be expressed by a functor F: C

Bank_Client

→

SimpleUML

that contains:

– A model element mapping

element

= Bank

→

Class ; Client

→

Class ; Bank_Client

→

Association

–

A model link mapping F

navigation

(Bank,[forward],[Bank_Client])

→

{(Class,[forward],[Association]) ;

(Client,[reverse],[Bank_Client])

→

(Class,[reverse],[Association]) ;

(Bank_Client,[source],[Bank])

→

(Association,[source],[Class]) ;

(Bank_Client,[destination],[Client])

→

(Association,[destination],[Class])

113

Table 1. Model elements and model links of Bank_Client and SimpleUML model

Bank_Client

SimpleUML

elements {Bank,Client,Bank_Client} {Class, Association}

links/ basic

navigations

{(Bank,[forward],[Bank_Client]),

(Client,[reverse],[Bank_Client]),

(Bank_Client,[source],[Bank]),

(Bank_Client,[destination],[Client])}

{(Class,[forward],[Association]),

(Class,[reverse],[Association]),

(Association,[source],[Class]),

(Association,[destination],[Class])}

Table 2. Navigation mapping and mapping of a composition

From Bank_Client To SimpleUML

(Bank,[forward],[Bank_Client]) (Class,[forward],[Association])

(Bank_Client,[destination],[Client]) (Association,[destination],[Class])

(Bank,[forward],[Bank_Client]) °

(Bank_Client,[destination],[Client])=

(Bank,[forward,destination],[Bank_Client,Client])

(Class,[forward],[Association]) °

(Association,[destination],[Class])=

(Class,[forward,destination],[Association,Class])

Remarks. The mapping of the composition of two navigations is the composition of

the mappings of the two navigations. This is an important property of the structural

mapping and is called structure-preserving mapping in the category theory.

4 Exploiting the formalization

In order to demonstrate the benefits of the proposed formalization, we have developed

a prototype of an MDE environment in which different kind of data such as models,

meta-models, mapping specifications, conformance relationships and more generally,

any structure-preserving relationship can be represented in a unified manner (using

categories and functors).

The developed prototype having architecture depicted in Fig.6 contains an OCL

evaluator that exploits categorical representations of models and conformance

mapping to navigate through model elements. The implementation of this evaluator is

well facilitated since model navigation – an important part of the language is made

explicit in the categorical representation of (meta-)models.

Modu le Model/

Category

Module OCL (parser and evaluator)

Modu le Set

Module Transformation Engine

ModuleTracking/

Impact Analyse

Mode l Query/

Model Checker

(formal) Subset of QVTTracking/Impact analyse…

Fig. 6. The MDE environment prototype

The developed prototype has allowed us to point out several potential usages of the

formalization presented in the previous sections. Some of these usages are provided

below:

– Verifying for model conformance: the input and output model of a transformation

can be respectively verified if each model conforms to its meta-model due to the

OCL evaluator.

– Model query: models can be queried with the OCL language.

114

– Model transformation execution: a set of model transformations (structure

preserving transformation) can be executed due to the transformation engine.

– Systematic traceability: the traceability information is stored as categorical

functors and is produced as explicit result of transformation together with output

model.

– Tracking for multi-step transformations: since traceability information is stored in

the form of functors, those functors can be composed in the case of successive

transformation.

– Help to the analysis of impacts: since the structural relation between input and

output model is captured by a functor (this functor is also the traceability

information), it is possible to ask some kind of questions about transformation

executed such as: if a model element (or model link) in the input model is removed

then which parts of the output model will change? Or in the inverse direction: if I

want to make some change in the output model, which parts of the input model

need to be changed? These kind of questions can be answered without making real

change and re-execute transformations and is very useful in an interactive

environment where model transformation is an interactive computer aided tool to

the development or may be in the specification phase of model transformation

when debugging facility is a requirement.

– Analysis for (structural) completeness of model transformations: with the

traceability information we can easily verify which parts of the input model do not

take part in the generation of any model element in the output model, this may be

the case in that the specification of model transformation is not complete.

5 Related works

Category theory has been used to formalize UML [14] and recently MOF [4]. These

formalizations based on Slang, a language supporting category theory of the Kestrel

Institute [14]. Our formalization uses directly the graph representation (interpreted as

categories) of models, functors to describe conformance mapping and OCL to

describe constraints. In our work, functor is also used to represent relation between

models at different levels of abstraction of the same system.

6 Conclusions

The work presented in this paper bases on a categorical abstraction of model and OCL

to formalize the conformance relation of a model to its meta-model in the Object-

Oriented Modeling TS. This relation can be expressed by a conformance mapping

from the model to its meta-model and a set of constraints associated to the meta-

model. These constraints must be satisfied when being evaluated over the model, the

meta-model and the conformance mapping between them. We believe that the same

kind of formalization can be used to other TSs due to the conformance mapping from

a model to its definition (meta-model) in OOM TS or from a XML document to its

DTD (or XML Schema), etc. The main advantage of this formalization is that it is

115

very abstract and can be applied to any kind of (meta-)models. This formalization is

also a first step in defining a model transformation formalism in which traceability

and analysis of impacts is fully supported.

References

1. Colin Atkinson. Meta-Modeling for Distributed Object Environments. In The First

International Enterprise Distributed Object Computing Conference (EDOC '97) , pages 90-

103, Brisbane, Australia, October 1997. IEEE Computer Society Press.

2. Jean Bézivin. On the Basic Principles of Model Driven Engineering. In MDE for Embedded

System Summer School, Brest, France, September 2004. ENSIETA.

3. Jean Bézivin. On the unification power of models. SoSym, 2005.

[http://www.sciences.univ-nantes.fr/lina/atl

/www/papers/OnTheUnificationPowerOfModels.pdf]

4. Kenneth Baclawski, Mieczyslaw Kokar, and Jeffrey Smith. Metamodeling facilities. [

http://www1.coe.neu.edu/%7Ejsmith/Publications/mof.pdf ]

5. Denilson Barbosa, Alberto O. Mendelzon, Leonid Libkin, Laurent Mignet, and Marcelo

Arenas. Efficient Incremental Validation of XML Documents. In ICDE, 2004. [

http://www.cs.toronto.edu/~marenas/publications/icde04.pdf ]

6. Tim Bray, Jean Paoli, C. M. Sperberg-McQueen, Eve Maler, and François Yergeau.

Extensible Markup Language (XML) 1.0 (Third Edition). W3C, February 2004. [

http://www.w3.org/TR/2004/REC-xml-20040204/ ]

7. Michael Barr and Charles Wells. Category Theory - Lecture Notes for ESSLLI. Lecture

Notes, 1999. [ http://www.folli.uva.nl/CD/1999/library/pdf/barrwells.pdf ]

8. Joseph A. Goguen. A Categorical Manifesto. Mathematical Structures in Computer

Science, 1(1):49-67, 1991.

[ http://citeseer.ist.psu.edu/goguen91categorical.html ]

9. Kathleen Jensen and Niklaus Wirth. Pascal User Manual and Report. Springer-Verlag,

1976.

10. I. Kurtev, J. Bézivin, and M. Aksit. Technical spaces: An initial appraisal. In CoopIS, DOA

2002 Federated Conferences, Irvine, 2002.

[http://www.sciences.univ-nantes.fr/lina/atl/www/papers/PositionPaperKurtev.pdf]

11 Tom Mens. A Formal Foundation For Object-Oriented Software Evolution. PhD thesis,

Vrije Universiteit Brussel, August 1999.

12. David E. Rydeheard and Rod M. Burstall. Computational Category Theory. Series in

Computer Science. Prentice Hall International, 1988.

[ http://www.cs.man.ac.uk/~david/categories/book/book.pdf]

13. Mark Richters. A Precise Approach to Validating UML Models and OCL Constraints. PhD

thesis, Universität Bremen, 2002.

[ http://www.db.informatik.uni-bremen.de/teaching/courses/ss2002_oose/m.pdf]

14. Jeffrey E. Smith. UML Formalisation and Transformation. PhD thesis, Northeastern

University, Boston, Massachusetts, December 1999.

15. Jaap van Oosten. Basic Category Theory. In Basic Research in Computer Science, BRICS

Lecture Series. University of Aarhus, January 1995.

[ http://www.brics.dk/LS/95/1/BRICS-LS-95-1/BRICS-LS-95-1.html]

16. Jos Warmer and Anneke Keleppe. The Object Constraint Language, Precise Modeling

With UML. Object Technology Series. Addison-Wesley, 1999.

116