Tree Automata for Schema-level Filtering of XML
Associations
Vaibhav Gowadia and Csilla Farkas
Information Security Laboratory
and
Department of Computer Science and Engineering
University of South Carolina, Columbia, SC 29208
Abstract. In this paper we present query filtering techniques based on bottom-
up tree automata for XML access control. In our authorization model (RXACL),
RDF statements are used to represent security objects and to express the security
policy. Our model allows to express and enforce access control on XML trees
and their associations. We propose a query-filtering technique that evaluate XML
queries to detect disclosure of association-level security objects. A query Q dis-
closes a security object o iff the (tree) automata corresponding to o accepts Q.
We show that our schema-level method detects all possible disclosures, i.e., it is
complete.
1 Introduction
Several XML access control models have been developed recently [1–6]. They allow
node-level security granularity by assigning access restrictions to the nodes and links
of XML documents. However, none of these models provide access control for data
associations. Intuitively, an association security object is an XML subtree that is disal-
lowed to be accessed by a user, while all of its proper subtrees are permitted separately.
Incorporating association in an access control model increases data availability while
preserving confidentiality.
The RXACL architecture, introduced in [7], provides flexible access control gran-
ularity by allowing security classification of XML nodes and subtrees (simple security
objects), and associations among nodes (association security objects). In [7] we pro-
posed a technique to enforce association-based access control at data-level (i.e., check
for security violation after query processing) and it is outside the scope of this paper.
In this paper we extend RXACL architecture by presenting techniques for performing
security check before the query is processed. Our work is similar to those proposed by
Murata et al. [5] and Luo et al. [6]. However, their method supports node-level security
objects only. The automata model, used by them is not sufficient to model association-
level security objects. In this paper, we use bottom-up tree automata to represent secu-
rity objects.
0
This work was partially supported by National Science Foundation grant number IIS-0237782.
Gowadia V. and Farkas C. (2005).
Tree Automata for Schema-level Filtering of XML Associations.
In Proceedings of the 3rd International Workshop on Security in Information Systems, pages 136-145
DOI: 10.5220/0002575401360145
Copyright
c
 SciTePress

We propose a data-independent technique to recognize disclosure of association
level security objects by XML queries. Results of our analysis can be (1) association
objects are disclosed, (2) association objects are not disclosed, or (3) association objects
may be disclosed. Options 1 and 2 indicate that the query should be rejected or accepted,
respectively. If the third option is reached, data-level analysis is required to evaluate
whether a security violation is present or not.
We present a two-layered association filtering method. First we detect disclosure of
association in a given query-pattern, i.e., information encoded in the XML query itself.
Second, we extend query-pattern with document schema to represent all schema infor-
mation that the query answer would reveal to a user. XML query-patterns are labeled-
trees where node labels may be variables, constants, or the special symbol ’//’(self-
or-descendant axis [8]). We model association security objects with pattern automatas
(Definition 8). A pattern automata takes (extended) query-patterns as input and reaches
an accepting state if and only if the input discloses the security object represented by it.
The main technical contributions of this paper are the development of pattern automatas
for security objects and the notion of extended query-pattern. We present algorithms to
construct query-pattern, pattern automata, and to detect disclosure of security objects.
The organization of the paper is as follows: next section presents an overview of
RXACL architecture and query filtering mechanism. Section 3 introduces formal defin-
itions of basic constructs used in this paper. Section 4 presents algorithms for construct-
ing query-pattern, association pattern automata and to detect association disclosure.
Section 5 introduces the notion of extended query-pattern and presents a schema-level
security analysis of query. We conclude in section 6 and list future work.
2 RDF-based XML Access Control Architecture
Figure 1 shows the RXACL architecture. The architecture contains four main compo-
nents: 1. Query filter 2. Query engine, 3. Data level access control, and 4. User history.
The query filtering component performs schema-level analysis to determine whether
answer to the input query : (1) violates access control policy (violating), (2) does not
violate the access control policy (safe), or (3) requires a data-level security check to de-
tect possible violations (unsafe). The XML query engine is responsible for generating
responses to user’s requests. RXACL uses an existing XML query engine, the devel-
opment of such an engine is outside of the scope of this paper. The data-level access
control component analyzes the query-answer based on the security policy and data
previously released to the user [7]. The history component keeps track of answered
query-patterns and data released to each user.
1
When a data request is submitted to a RXACL system, query filtering component
first checks for disclosure of disallowed association-level security objects in the query
(without utilizing the XML schema information). If a disallowed association-level secu-
rity object is disclosed, the query is immediately rejected. Otherwise, the query-pattern
is extended with schema information and query-patterns of previously answered queries
to the user. Extended query-pattern are now checked for disallowed objects. If no disal-
lowed association-level security object is disclosed in extended query-pattern the query
1
Due to space limitation the handling of the history file is not presented in this manuscript.
137

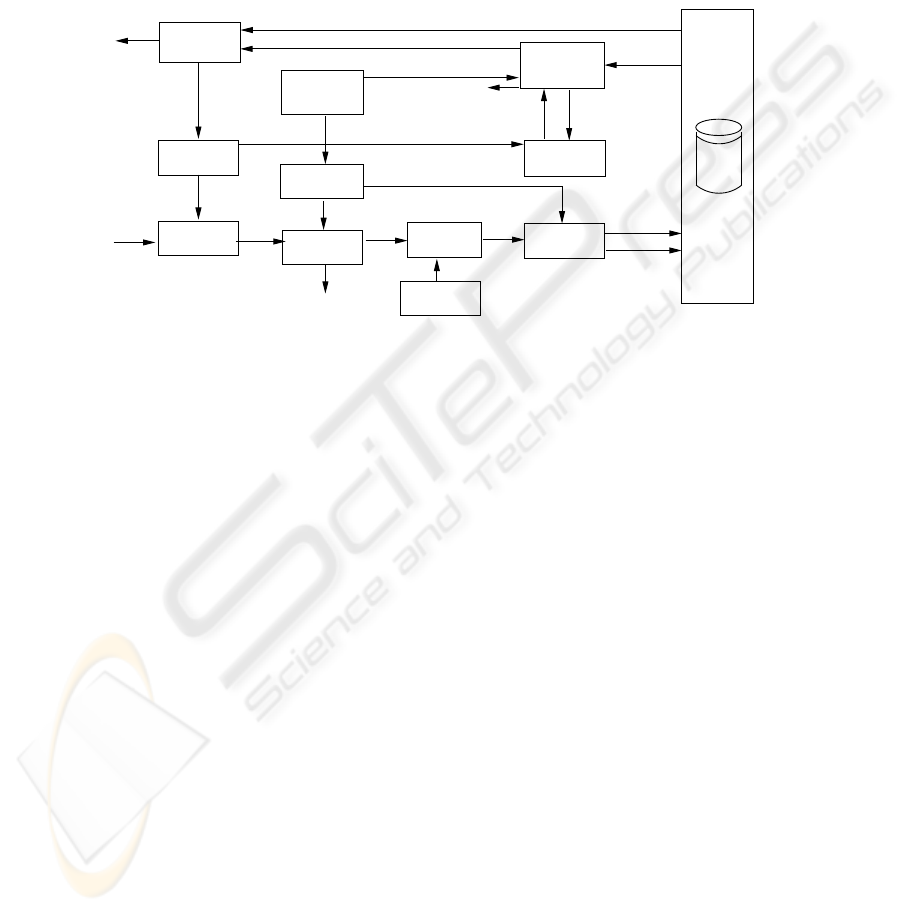
answer is labeled safe. Otherwise, it is labeled unsafe. The query is submitted to XML
query engine for further processing. The result of unsafe query’s evaluation are further
evaluated for possible data-level violations as described in [7]. Answer to safe queries
is returned to user without further security analysis. For all queries that are answered,
user history is updated with query-pattern and released data. The assurance of our query
level filtering is based on the completeness property of the filtering.
Answer
11.
11.
9.
1. Query
14. No Violation
12. Unsafe
Security Check
Data Level
12. Safe Answer
Violation
7. No
3.
15.
10
18.
13.
5.
4.
2.
File
History
Automata
Generate Pattern
Update
History
13, 19. Return Answer
8.
17. Reject (violation)
No Violation
16. Return Trees
17.
(Unsafe Query)
Violation
Policy
(RXACL)
Unite
Query Patterns
Query Pattern
Extend
Schema
(Safe Query)
No Violation
Tree Extension
Security
Disclosure
Check
Check
Disclosure
6. Reject Query (Violation)
XML
Store
Fig.1. RXACL architecture for enforcing XML access control
3 Definitions
This section describes definitions necessary to model XML queries , association objects,
and XML schema.
Definition 1. (Labeled-tree)
A labeled-tree, or a tree, is defined recursively as follows: (1) the empty set {} is a tree,
called the empty tree, (2) a single node {n} is a tree, and (3) if t
1
, t
2
, . . . , t
k
are trees,
then {n → {t
1
, t
2
, . . . , t
k
}} is a tree. In this case we say that {n → {t
1
, t
2
, . . . , t
k
}}
represents the tree whose root n has outgoing edges to subtrees t
1
, t
2
, . . . , t
k
.
The nodes of the trees are labeled. Labels may be constants, node variables (corre-
sponding to any node value), or path variables (corresponding to any path). Constants
correspond to element, attribute and text values. Nodes labeled with text-values are
called text nodes and are always leaf nodes. Attribute nodes can have only on child
node, a text node. Also, any two attribute nodes of a given element cannot have same
label. Element nodes can have zero or more child nodes that can be elements, attributes,
or text nodes. We denote element nodes with n
i
, attribute nodes with a
i
, and text nodes
with pcdata.
138

A labeled tree is called a ground tree if all of its nodes are labeled with constants. An
XML instance T is a ground-tree.
Definition 2. (Path-expression)
Let p = {n, {a
1
, . . . , a
j
}} represent a single node n and its child nodes corresponding
to attributes a
1
, . . . , a
j
, where n is either a constant, or a variable. A path-expression
is defined as: 1. p is a path expression, 2. {p
1
→ p
2
→ . . . → p
k
} is a path-
expression where p
i
(i = 1, . . . , k) are path-expressions, 3. Let // denote an arbitrary
path-expression. Then the following are also path-expressions: {// → p
1
→ . . . →
p
m
}, {p
1
→ // → p
m
}.
DTD [9] and W3C XML Schema [10] satisfy a constraint that all child nodes of any
given node must have unique names. Trees satisfying this constraint are called single-
type tree [11]. Path-expressions are single-type trees.
We consider XQuery syntax [12] of the following form:
Definition 3. (XML Query)
An XML query Q is of the following form:
FOR v
0
in P
0
LET v
1
:= P
1
, . . . , v
l
:= P
l
RETURN {n → {
v
k
, . . . , v
j
}}
WHERE (v
i
== v
j
and . . . and v
l
== v
m
)
where, v
i
(i = 0, . . . , l) are variables of query (we refer to them as query-variables
in rest of this paper),
v
i
(i = 0, . . . , m) represent a path-expression {v
i
→ p
′
} (i =
1, . . . , l) and p
′
is a path-expression that does not contain any query-variables, P
i
(i =
0, . . . , l) are path-expressions, and n is a constant.
Given a XML query Q, the first step in query filtering architecture is to build query-
pattern of Q. Let V = {v
1
, v
2
, . . . , v
l
} be the set of query-variables defined in Q, and
V = {v
1
, v
2
, . . . , v
m
} be the path-expressions in the RETURN or WHERE clause of
the query. Intuitively, the query-pattern is constructed by uniting the path-expressions in
V . Since path-expressions may contain query-variables. We need a method to eliminate
query variables. A formal definition of variable-substitution follows.
Definition 4. (Variable-Substitution)
Let $v
i
= {p
1
→ . . . → p
l
}, and $v
j
= {$v
i
→ p
′
1
→ . . . p
′
m
} be two assignments in
the FOR or LET clause of the XML query. A variable substitution replaces $v
i
in the
second assignment with {p
1
→ . . . → p
l
}.
Example 1. Consider the single-type tree T = {$x → {a, d}}, where $x = {// →
{r}} is a query-variable. Substituting $x, we get T = {// → {r → {a, d}}}. 2
Definition 5. (Single-type Tree-Merge)
Let P
1
= {n
1
1
→ n
1
2
→ . . . n
1
k
→ n
1
k+1
→ . . . n
1
l
} and P
2
= {n
2
1
→ n
2
2
→ . . . n
2
k
→
n
2
k+1
→ . . . n
2
m
} be two ground path-expressions over the same schema. We define
merge of path expressions as follows:
if n
1
1
= n
2
1
, n
1
2
= n
2
2
, . . . , n
1
k
= n
2
k
, and n
1
k+1
6= n
2
k+1
, then
P
1
∪
S
P
2
= {n
1
1
→ n
1
2
. . . n
1
k
→ {{n
1
k+1
→ . . . → n
1
l
}, {n
2
k+1
→ . . . → n
2
m
}}.
139

We extend the notion of merging paths to merging single-type trees. Let T
1
= {n →
{t
1
, t
2
, . . . , t
k
}} and T
2
= {n
′
→ {t
′
1
, t
′
2
, . . . , t
′
l
}} be two trees, then their merger
T
1
∪
S
T
2
is defined as follows:
1. T ∪
S
{}
def
= {} ∪
S
T
def
= T
2. if n 6= n
′
, T
1
∪
S
T
2
= {T
1
, T
2
},(trees cannot be merged).
3. if n = n
′
, then let T = {}. For all paths p originating from the root in T
1
and T
2
,
do T = T ∪
S
p. T
1
∪
S
T
2
= T .
The query-pattern of an XML query Q is a labeled-tree representing all data dis-
closed by Q, i.e., all data returned to the user or accessed by Q.
Definition 6. (Query-Pattern)
Let Q be the given XML query and P
1
, . . . , P
n
are path-expressions that occur in the
RETURN or the WHERE clause of Q. If P
i
== P
j
is a condition in the WHERE
clause, we add a new leaf node labeled with a data-variable v to P
i
and P
j
. Substitute all
query-variables in P
1
, . . . , P
n
. Query pattern P is the labeled-tree produced by merging
paths P
1
, . . . , P
n
. Algorithm 1 shows the construction of the query-pattern.
Example 2. Consider the following XML query Q
2
: FOR
$ x in //r LET $ y := $ x/d,
$ z := $ x/a RETURN <answer> {$z/c} </answer> WHERE { $ z/b == $ y }. Let T
r
be the tree in the return statement of Query Q
2
. T
r
specifies structure of query answer
being returned to the user. To evaluate the query-answer $z/b and $y must be accessed.
Query-pattern constructed from query Q
2
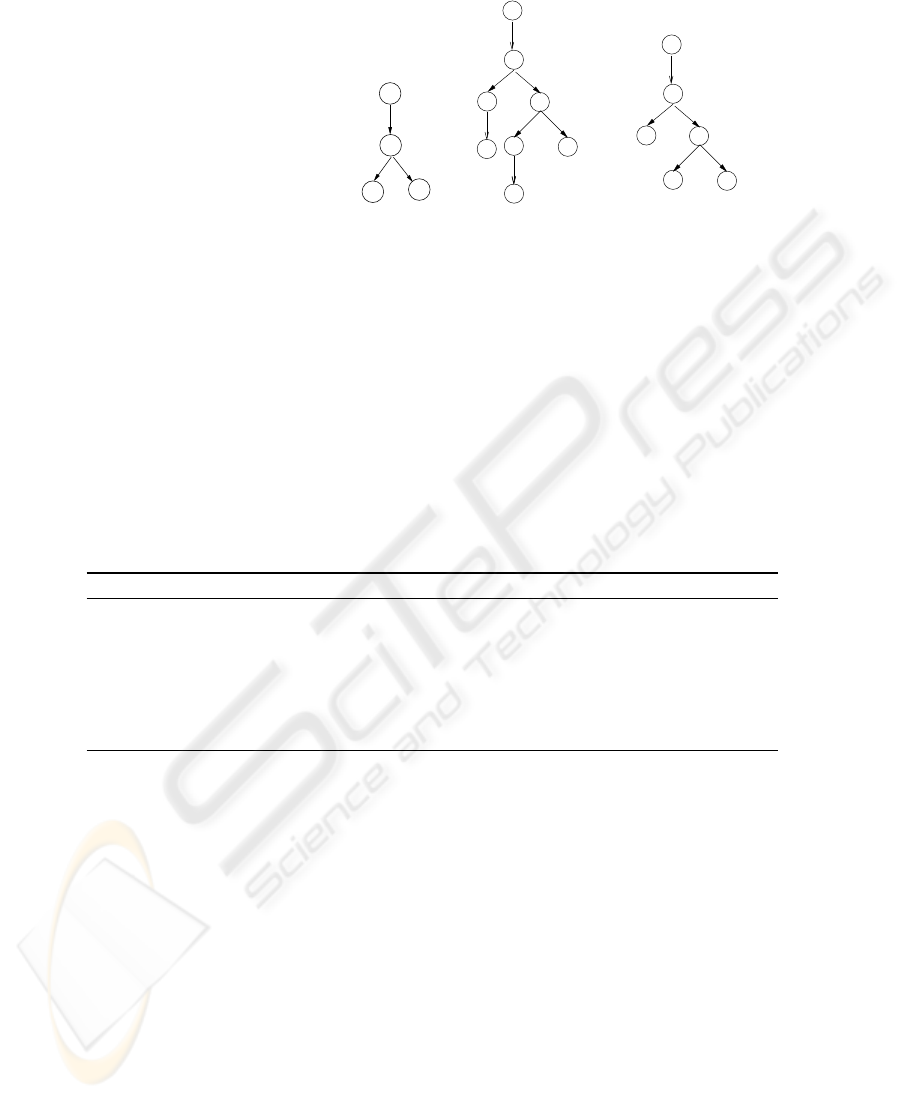
is shown in Fig. 2(c). 2
Algorithm 1: Algorithm to construct query-pattern
input : Query Q
output: Query-Pattern Tree T
Let V = {v
1
, . . . , v
k
} be the set of variables defined in Q.
Let P = {p
1
, . . . , p
m
} be the set of path-expressions in RETURN and WHERE clause of Q.
i ← 1
list ← {} /* List of sets, where each set contains path-expressions in WHERE clause of Q, such that their values are transitively equal*/
/* Extend the path-expressions with a data-variable, such that path-expressions equated in WHERE clause have same data-variable.*/
foreach expression (p
l
== p
n
) in WHERE clause of Q do
if p
l
∈ S and S is a set in list then
Append leaf node of p
l
to p
n
Add p
n
to S
else if p
n
∈ S and S is a set in list then
Append leaf node of p
n
to p
l
Add p
l
to S
else
Create a new data-variable v
i
Append v
i
to p
l
and p
n
Create a set S = {p
l
, p
n
}
Add S to list
i ← i + 1
/* Removing query-variables from path-expressions*/
for i := 1 to m do
Let T
i
← p
i
, where p
i
∈ P
Let r ← root node of T
i
repeat
Substitute r in T
i
, with its assigned value (by := or in operator ) in Q
r ← root node of T
i
until r is a constant or ’//’
/* Uniting path-expressions to obtain query-pattern */
Initialize T ← {}
for i := 1 to m do
T ← T ∪
S
T
i
return T
140

Definition 7. (Protection Object)
A simple security object o is a node-labeled tree, where all distinct subtrees t
1
, t
2
, . . . , t
k
of o have the same access permission as o. That is, for every proper subtree t
i
∈ o,
λ(o) = λ(t
i
), where λ(o) and λ(t
i
) denote the security classification of o and t
i
respec-
tively. Simple security objects are equivalent to node-level security classification. An
association security object o is a node-labeled tree where every proper subtree t
i
∈ o,
λ(o) > λ(t
i
) (i = 1, . . . , n).
We construct Pattern Automatas (PA) (similar to the tree-automatas in [13, 14]) to
represent security objects.
Definition 8. (Pattern Automata)
Let E be a set of node-labels for elements, A be a set of node-labels for attributes,
and let the label pcdata represent all text nodes. A Pattern Automata is defined as X =
{Σ, Q, q
0
, Q
f
, δ}, where Q = {q
0
, . . . , q
n
} is a finite set of automaton states, Σ =
E ∪ A ∪ {pcdata, //} is automata alphabet, ’//’ is a symbol for self-or-descendant axis,
q
0
is start state, Q
f
⊂ Q, (q
0
6∈ Q
f
) is set of accepting final states, and δ is set of state
transition rules.
Let σ ∈ Σ is label of scanned node N of a query pattern and therefore the next input
symbol for the automata, and Q
c
⊆ Q is set of states associated with child nodes of N.
A valid transition is of the form, σ(q
i
, . . . , q
j
) → q
k
, where {q
i
, . . . , q
j
} ⊆ Q
c
, and q
k
is state associated with N after scanning. For simplicity, we will often write transition
rule in the form σ(Q
t
) → q
k
, where Q
t
= {q
i
, . . . , q
j
} is set of states required for
transition. To distinguish data values from labels of elements and attributes, we write
data values inside [ ]. If δ does not contain a valid transition rule, by default the state
associated with the scanned node is q
0
.
4 Security Analysis of Query Pattern
RXACL performs security analysis by evaluating query-pattern with the pattern au-
tomatas corresponding to protection objects. An accepting state is reached if the pro-
tection object is disclosed by the input pattern. These automatas can also be used for
recognizing possible disclosure of security objects by query-patterns extended with doc-
ument schema as discussed later in section 5.
A pattern automaton X accepts a query-pattern P iff there is at least one accepting
path of transitions that reads complete P. For clarity, in this paper we allow use of
wildcard symbol (∗) to represent any alphabet symbol. Let us now consider an example.
Example 3. The following automaton X
3
= {Σ, Q, q
0
, Q
f
, δ} is a XML Pattern Au-
tomata that accepts query patterns disclosing association A
2
(see Fig. 2(b)). An ac-
cepting run of this automaton on query Q
2
is shown in Fig. 2(d). It means that answers
of Q
2
disclose A
2
. 2
We now present an algorithm (See Alg. 2 and Proc. AddRules) to generate pattern
automata for associations.
2
Given a query-pattern P a pattern automaton X is gener-
ated, such that on input P
′
, X accepts iff P is contained in P
′
. Algorithm 2 performs
2
Full version of our security analysis algorithms is given in technical report available at
http://www.cse.sc.edu/research/isl/
141

Q = {q
0
, q
a
, q
b
, q
c
},
Σ = {a, b, c, //},
q
0
= q
0
,
Q
f
= {q
a
},
δ = { b() → q
b
,
c() → q
c
,
a(q
b
, q
c
) → q
a
,
∗(q
a
) → q
a
}
a
c
//
b
b
c
a
d
r
//
1
v
1
v
c
a
d
b
r
//
a
q
0
q
0
q
a
q
a
q
0
q
b
q
c
q
0
q
(a) (b) (c) (d)
Fig.2. (a) Pattern automata example X
3
(b) Example association A
2
(c) Query-pattern of Q
2
(d)
States of X
3
(q
i
) on query-pattern of Q
2
as input.
a bottom up traversal of the association security object (a labeled-tree). At each step of
traversal the label of current node is read. If the label is read for first time, it is added
to pattern automaton’s alphabet and a new state is also created. If the label denotes a
self-or-descendant edge in the query-pattern then a transition rule with a wildcard (*)
for read symbol is added to the pattern automata. Otherwise transition rule with symbol
read at the current node is added.
Algorithm 2: Algorithm to generate pattern automata
input : Association pattern P
output: Pattern Automata X = {Σ, Q, q
0
, Q
f
, δ}
Q ← {q
0
}
Σ ← {//, pcdata}
Q
f
← {}
δ ← {}
X ← {Σ, Q, q
0
, Q
f
, δ} Let S be a global stack
S ← ∅ /* S is a global stack used to remember states of child nodes during bottom-up traversal of P */
X ← AddRules (P, X)
Q
f
← pop(S)
return X
Theorem 1. Let Q be an XML query, P the query-pattern generated from Q (Def. 6), O
an association object and AO the association-automata representing O. The association-
automata AO accepts a input query-pattern P iff there exists an XML instance I such
that the answer to Q over I discloses O.
Proof Sketch: (⇒) The pattern-automata performs bottom-up traversal of P , i.e., states
of child nodes are evaluated before evaluating state for root node. Let n be a node in P
scanned to detect disclosure of O. If n is a leaf node in O, there must exist a valid transi-
tion of form {n() → q} ∈ δ, where δ is the transition function of pattern-automata AO
created by Algorithm 2. If n is an internal node with child nodes {n
1
, . . . , n
k
}, Algo-
rithm 2 generates a transition rule of the form {n(q
1
, . . . , q
k
) → q}, where q
1
, . . . , q
k
are states associated with n
1
, . . . , n
k
respectively. Clearly there exists an accepting path
142

Procedure AddRules(Root, Pattern Automata)
input : Pattern tree P, Pattern Automata X = {Σ, Q, q
0
, Q
f
, δ}
output: Modified Pattern Automata X
root ← root node of P
Qc ← {}
list ← child nodes of root
foreach node in list do
X ← AddRules( node, X) /* Perform bottom-up tree traversal */
if list 6= ∅ then
n ← Length of list
while n > 0 do
Q
c
← Q
c
∪ pop(S) /*Retrieve automata states after scanning child nodes */
n ← n − 1
label ← LabelOf(root)
if label = ’//’ then
foreach state q ∈ Q
c
do
δ ← δ ∪ {∗(q) → q}}
else
Find set of transition rules R, of the form {label (Q
′
) → q} in δ
if R is empty then
Create a new state q
new
/* label(Q
′
) is read for the first time*/
Q ← Q ∪ {q
new
}
δ ← δ ∪ {label(Q
c
) → q
new
}
push(S,{q
new
})
else if Q
c
6= Q
′
for all rules in R then
Create a new state q
new
/* Transitions exist for labelQ
′
but are not applicable*/
Q ← Q ∪ {q
new
}
δ ← δ ∪ {label(Q
c
) → q
new
}
push(S,{q
new
})
else
push(S,{q}) /* An existing transition leading to state q is applicable*/
return X
of automata evaluation if the association pattern is traversed. Thus, pattern-automata
finds the accepting path if it exists.
(⇐) For this, we show how to construct instance I such that the answer to Q over I
must contain O. Let ζ be a mapping from P to O with following properties: ζ maps (1)
a constant to the same constant, (2) variable to pcdata , and (3) a arbitrary path p to //.
If there exists a ζ such that the pattern P
′
created from P by replacing all variables
of P with ζ(v) and p with //, and O is a subtree of P
′
then we generate I as follows:
(1) replace all mapped variables v ∈ P with ζ(v), (2) replace all non-mapped variables
in P with pcdata c, and (3) replace // with the empty path, i.e., remove //.
5 Security Analysis of Extended Query-Pattern
In addition to the structural information contained in the RETURN and the WHERE
clauses of the query, a query answer also contains subtrees of the original XML doc-
ument, where each returned subtree originates from one of the path-expressions in the
RETURN clause. To incorporate this knowledge in our model, we define the notion of
extended query-pattern.
Definition 9. (Extended Query-Pattern)
Let P denote a query-pattern and S the schema (ground-tree) of the XML document
that Q is posed on. The extended-query-pattern (EQP) is defined as a set of trees
{T
1
, . . . , T
m
}, where T
i
(i = 1, . . . , m) are constructed as follows: Let ν denote a
symbol mapping from the symbols of P to the symbols of S such that: (1) for con-
stants ν is an identity mapping, (2) ν maps the data-variables to the empty node ∅,
143

and (3) ν maps ’//’ to any ground path in S. We extend ν to map paths of P , such
that given a path p = {n
1
→ n
2
→ . . . → n
l
}, its mapping ν(p) = {ν(n
1
) →
ν(n
2
) → . . . → ν(n
l−1
) → t
l
}, where t
l
is a tree rooted at ν(n
l
) such that ν(p) ∈ S.
Finally, given paths p
1
, . . . , p
k
of of all leaf nodes in P we construct T
i
∈ EQP as
T
i
= ν(p
1
) ∪
S
ν(p
2
) ∪
S
. . . ∪
S
ν(p
k
) and T
i
∈ S for all possible symbol mapping ν.
Theorem 2. Let Q be an XML query, S be the schema of XML document, EQP be
the query-pattern extended with S, O an association object, and AO be the association-
automaton representing O. If AO does not accept the extended query-pattern EQP ,
then the query is safe to answer for any XML document that satisfies S. That is for all
XML instances over S the query Q will not disclose O.
Proof Sketch: Lets assume by contradiction that the query Q discloses an association
object AO and the pattern-automata generated from AO does not accept the extended
query-pattern. But then, either the specifying query itself discloses O, i.e., the union of
the paths p
1
, . . . , p
k
in the FOR, LET, RETURN, and WHERE clause of Q disclose
O, or the answer generated from any XML instance conforming to S together with
p
1
∪
S
p
2
∪
S
. . . ∪
S
p
k
disclose O. But this is exactly the information used to generate
the extended query-pattern. Using Theorem 1 this implies that the tree-automata must
accept the extended query-pattern, which is a contradiction.
6 Conclusions
In this paper we have presented a bottom-up tree automata (pattern-automata) based
technique for filtering XML association before query evaluation. We have also given
algorithms for constructing query-pattern, pattern automata, detect disclosure of as-
sociation security object in a query-pattern itself and query-pattern is extended with
schema information. We have also shown that our security-analysis is complete, i.e.,
our method detects all possible disclosures.
We have considered only simple XQueries in this work. In future, we plan to extend
our analysis to incorporate nested queries. At present our schema-level analysis requires
the schema to be a single-type tree language (DTD or W3C XML schema). We also plan
to extend our schema-level security analysis to incorporate regular tree languages, like
RELAX NG.
References
1. Bertino, E., Castano, S., Ferrari, E.: Securing XML Documents with Author-X. IEEE Inter-
net Computing 3 (2001)
2. Bertino, E., Castano, S., Ferrari, E., M.Mesiti: Specifying and Enforcing Access Control
Policies for XML Document Sources. In: World Wide Web Journal. Volume 3. Baltzer
Science Publishers (2000)
3. Damiani, E., di Vimercati, S.D.C., Paraboschi, S., Samarati, P.: XML Access Control Sys-
tems: A Component-Based Approach. In: IFIP WG11.3 Working Conference on Database
Security, The Netherlands (2000)
144

4. Kudo, M., Hada, S.: XML Document Security based on Provisional Authorizations. In: Proc.
of the 7th ACM conference on Computer and Communications Security, Athens, Greece
(2000)
5. Murata, M., Tozawa, A., Kudo, M., Hada, S.: XML Access Control using Static Analysis.
In: CCS ’03: Proceedings of the 10th ACM conference on Computer and communications
security, ACM Press (2003) 73–84
6. Luo, B., Lee, D., Lee, W.C., Liu, P.: QFilter: Fine-Grained Run-Time XML Access Con-
trol via NFA-based Query Rewriting. In: Proc. of ACM Conference on Information and
Knowledge Management (CIKM). (2004)
7. Gowadia, V., Farkas, C.: RDF metadata for XML Access Control. In: Proceedings of the
2003 ACM workshop on XML security, ACM Press (2003) 39–48
8. W3C Recommendation: XML Path Language (XPath) Version 1.0. (1999)
9. Bray, T., Paoli, J., Sperberg-McQueen, C.M.: Extensible Markup Language Language 1.0
specification. W3C Recommendation. (2000)
10. Thompson, H.S., Beech, D., Maloney, M., Mendelsohn, N.: XML Schema Part 1: Structures.
Technical report, W3C Consortium (2001)
11. Murata, M., Lee, D., Mani, M., Kawaguchi, K.: Taxonomy of XML Schema Languages
using Formal Language Theory. ACM Trans. on Internet Technology (2005)
12. Fern
´
andez, M., Malhotra, A., Marsh, J., Nagy, M., Walsh, N.: XQuery 1.0 and XPath 2.0
Data Model. Technical report, W3C (2003) W3C Working Draft 12 November 2003.
13. Chidlovskii, B.: Using Regular Tree Automata as XML Schemas. In: ADL ’00: Proceedings
of the IEEE Advances in Digital Libraries 2000, IEEE Computer Society (2000) 89
14. Neven, F.: Automata theory for XML researchers. SIGMOD Rec. 31 (2002) 39–46
145