Indexation of Document Images Using Frequent Items

Eugen Barbu, Pierre Heroux, Sebastien Adam and Eric Trupin

Laboratoire Perception Systemes Information CNRS FRE 2645, University Of Rouen, Place

E. Blondel, 76 821 Mont Saint Aignan cedex, France

Abstract. Documents exist in

different formats. When we have document

images, in order to access some part, preferably all, of the information

contained in that images, we have to deploy a document image analysis

application. Document images can be mostly textual or mostly graphical. If,

for a user, a task is to retrieve document images, relevant to a query from a set,

we must use indexing techniques. The documents and the query are translated

in a common representation. Using a dissimilarity measure (between the query

and the document representations) and a method to speed-up the search process

we may find documents that are from the user point of view relevant to his

query. The semantic gap between a document representation and the user

implicit representation can lead to unsatisfactory results. If we want to access

objects from document images that are relevant to the document semantic we

must enter in a document understanding cycle. Understanding document

images is made in systems that are (usually) domain dependent, and that are not

applicable in general cases (textual and graphical document classes). In this

paper we present a method to describe and then to index document images

using frequently occurences of items. The intuition is that frequent items

represents symbols in a certain domain and this document description can be

related to the domain knowledge (in an unsupervised manner). The novelty of

our method consists in using graph summaries as a description for document

images. In our approach we use a bag (multiset) of graphs as description for

document images. From the document images we extract a graph based

representation. In these graphs, we apply graph mining techniques in order to

find frequent and maximally subgraphs. For each document image we construct

a bag with all frequent subgraphs found in the graph-based representation. This

bag of “symbols” represents the description of the document.

1 Introduction

A document image analysis (DIA) system transforms a document image into a

description of the set of objects that constitute the information on the document and

which are in a format that can be further processed and interpreted by a computer [1].

Documents can be classified in mostly graphical or mostly textual documents [2]. The

mostly textual documents also known as structured documents respect a certain layout

and powerful relations exist between components. Examples of such documents are

technical papers, simple text, newspapers, program, listing, forms,… Mostly graphical

documents do not have strong layout restrictions but usually relations exist between

Barbu E., Heroux P., Adam S. and Trupin E. (2005).

Indexation of Document Images Using Frequent Items.

In Proceedings of the 5th International Workshop on Pattern Recognition in Information Systems, pages 164-174

DOI: 10.5220/0002576001640174

 SciTePress

different document parts. Examples of this type of documents are maps, electronic

schemas, architectural plans …

For this two categories of documents graph based representations can be used to

describe the image content (e.g. region adjacency graph [3] for graphical and

Voronoi-based neighborhood graph [4] for textual document images).

This paper presents an approach similar with the “bag of words” method from

Information Retrieval (IR) field. We describe a document using a bag of symbols

found automatically using graph mining [5] techniques. In other words, we consider

as “symbols” the frequent subgraphs of a graph-based document representation and

we investigate if the description of a document as a bag of “symbols” can be

profitably used in a indexation and retrieval task.

The approach has the ability to process document images without knowledge of, or

models for document content. Frequent items are used in clustering of textual

documents [6], or in describing XML documents [7] , but we do not know any

similar approch in the DIA field.

This paper is one step from a plan that has as aim to study if the bag of symbols

approach can be successfully used in document image supervised classification,

indexation and clustering (see Fig. 1).

Fig. 1. The “ bag of symbols” applications on document images

The outline of this paper is as follows. In section 2 we present a graph

representation and how we create this representation from a document image. Section

3 presents the graph-mining method used, in section 4 we describe how we search

documents based on dissimilarities between bags of objects. Section 5 shows

experimental results. We conclude the paper and outline perspectives in section 6.

2 Graph representation

Eight levels of representation for document images are proposed in [8]. These levels

are ordered in accordance with their aggregation relations. Data array, primitive,

165

lexical, primitive region, functional region, page, document, and corpus level are the

representation levels proposed.

Without loosing generality, in the following paragraphs we fix our attention on a

graph-based representation build from the primitive level. The primitive level

contains objects such as connected components (set of adjacent pixels with the same

color) and relations between them. From a binary (black and white) document image

we extract connected components. The connected components will represent the

graph nodes. On each connected component we extract features. In the actual

implementation the extracted characteristics are rotation and translation invariant

features based on Zernike moments [9]. The invariants represents the magnitudes of a

set of orthogonal complex moments of a normalized image.

Let I be an image and C(I) the connected components from I, if

)(ICc

∈

, c is

described as

, where id is a unique identifier and P the set of pixels the

component contains. Based on this set P, we can compute the center for the connected

component bounding box and also we can associate a feature vector to it. Based on

that,

. Subsequently using a clustering procedure on the feature

vectors we can label the connected component and reach the description

where l is a nominal label . The graph G(I) representing the image is

. Vertices V(I) correspond to connected components and are

labeled with component labels. An edge between vertex u and vertex w exists iff

),( Pidc=

Rvvyxidc ∈= ),,,,(

),,,( lyxidc=

))(),(( IEIVGG=

tywyuxwxu <−+−

))..()..((

,where t is a threshold that depends on the image I

global characteristics (size, number of connected components,…).

The following paragraph presents the clustering procedure used to associate each

connected component a label.

2.1 Labeling connected components

The two main categories of clustering methods are partitional and hierarchical.

Partitional methods can deal with large sets of objects (“small” in this context means

less than 300) but needs the expected number of clusters in input. Hierarchical

methods can overcome the problem of number of clusters by using a stopping

criterion [10] but are not applicable on large sets due to their time and memory

consumption.

In our case the number of connected components that are to be labeled can be

larger than the limit of applicability for hierarchical clustering methods. In the same

time we cannot use a partitional method because we do not know the expected

number of clusters. Based on the hypothesis that a “small” sample can be informative

for the geometry of data, we obtain in a first step an estimation for the number of

clusters in data. This estimation is made using an ascendant clustering algorithm with

a stopping criterion. The number of clusters found in the sample is used as input for a

partitional clustering algorithm applied on all data.

We tested this “number of cluster estimation” approach using a hierarchical

ascendant clustering algorithm [11] that employes Euclidean distance to compute the

dissimilarity matrix, complete-linkage to compute between-clusters distances, and

166

Calinsky-Harabasz index [10] as a stopping criterion. The datasets ( ) (see

Table 1.) are synthetically generated and contain well separated (not necessary

convex) clusters.

321

,, TTT

Table 1. Data sets description

T |T| no. of clusters

T1 24830 5

T2 32882 15

T3 37346 24

Table 2. Proposed number of clusters

T \ |S| 50 100 300 500 600 700

[6, 8, 7, 6, 5,

6, 6, 6, 5, 5]

[5, 7, 9, 7, 5,

5, 7, 5, 5, 7]

[7, 5, 7, 8, 7,

5, 5, 5, 7, 7]

[8, 7, 5, 5, 5,

5, 5, 5, 5, 5]

[5, 5, 5, 5, 5,

7, 7, 7, 7, 5]

[5, 5, 7, 5, 7,

5, 5, 7, 5, 5]

[9, 15, 15,

14, 13, 15,

13, 13, 14,

15]

[15, 15, 13,

15, 15, 15,

15]

[15, 15, 15,

15, 15, 15,

14]

[15, 15, 15,

15, 15, 15,

15]

[15, 15, 15,

15, 15, 15,

15]

[15, 15, 15,

15, 15, 15,

15, 15, 14,

15]

[11, 7, 9, 18,

7, 7, 6, 4,

14, 8]

[6, 14, 23,

21, 7, 17,

23, 16, 12,

11]

[22, 24, 23,

19, 23, 24,

24, 21,

21,24,] 24]

[21, 25, 25,

24, 22, 24,

23, 24, 24,

24]

[20, 25, 21,

24, 19, 23,

24, 25, 24,

22]

[23, 20, 21,

20, 25, 24,

24, 21, 25,

24]

Considering S the sample extracted at random from a test set, in Table 2 we

present predicted cluster numbers obtained for different sample sizes. After repeating

the sampling procedure for 10 times if the test set is for example |S|=50, we obtain a

set of estimations for the number of clusters. We can see that by using a majority

voting decision rule we can find the good number of clusters in most of the cases and

even when the sample size is very small (50 or 100) compared to the data set size.

We employed our sampling approach combined with the k-medoids clustering

algorithm [12] on the connected components data set from images in our corpus (see

section 5). The k-medoids clustering algorithm is a more robust version of the well

known k-means algorithm. The images from our corpus contain 6730 connected

components. The proposed number of clusters using ten samples of size 600 is

[16,14,17,16,16,19,7,17,15,16] and by considering the majority we use 16 clusters as

input to the partitional clustering algorithm.

After labeling the connected components (nodes in the graph) subsequently we

describe the way we add edges to the graph. The edges can be labeled or not (if

unlabeled the significance is Boolean: we have or have not a relation between two

connected components) and can be relations of spatial proximity, based on “forces”

[13], orientation or another criterion.In our actual implementation the distance

between centers of connected components is used (see Fig. 2). If the distance between

two connected components centers is smaller than a threshold, then an edge will link

the two components (nodes).

167

3 Graph mining

“The main objective of graph mining is to provide new principles and efficient

algorithms to mine topological substructures embedded in graph data” [5].

Mining frequent patterns in a set of transaction graphs is the problem of finding in

this set of graphs those subgraphs that occur more times in the transactions than a

threshold (minimum support). Because the number of patterns can be exponential this

problem complexity can also be exponential. An approach to solve this problem is to

start with finding all frequent patterns with one element, then all patterns with two

elements, etc in a level-by-level setting . In order to reduce the complexity different

constraints are used: the minimum support, the subgraphs are connected, and not

overlapped.

The first systems emerged from this field are SUBDUE and GBI [5]. These

approaches use greedy techniques and hence can overlook some patterns. The

SUBDUE system search subgraphs in a single graph using a minimum description

length-based criterion. Complete search for frequent subgraphs is made in an ILP

framework by WARMR [5]. An important advance is the introduction of the concept

of closed subgraph. A graph is said to be closed or maximal if it does not have a

super-graph with the same number of apparitions in the dataset [14]. The graph-

mining systems were applied to scene analysis, chemical components databases and

workflows. A system that is used to find frequent patterns in graphs is FSG (Frequent

Subgraph Discovery) that “finds patterns corresponding to connected undirected

subgraphs in an undirected graph database”[15].

In our document image analysis context we are interested in finding maximal frequent

subgraphs because we want to find symbols but to ignore their parts.

The input for the FSG program is a list of graphs. Each graph represents a

transaction. We present subsequently how we construct the transactions list starting

from a set of document images. Using the procedure presented in section 2 we create

for each document an undirected labeled graph.

168

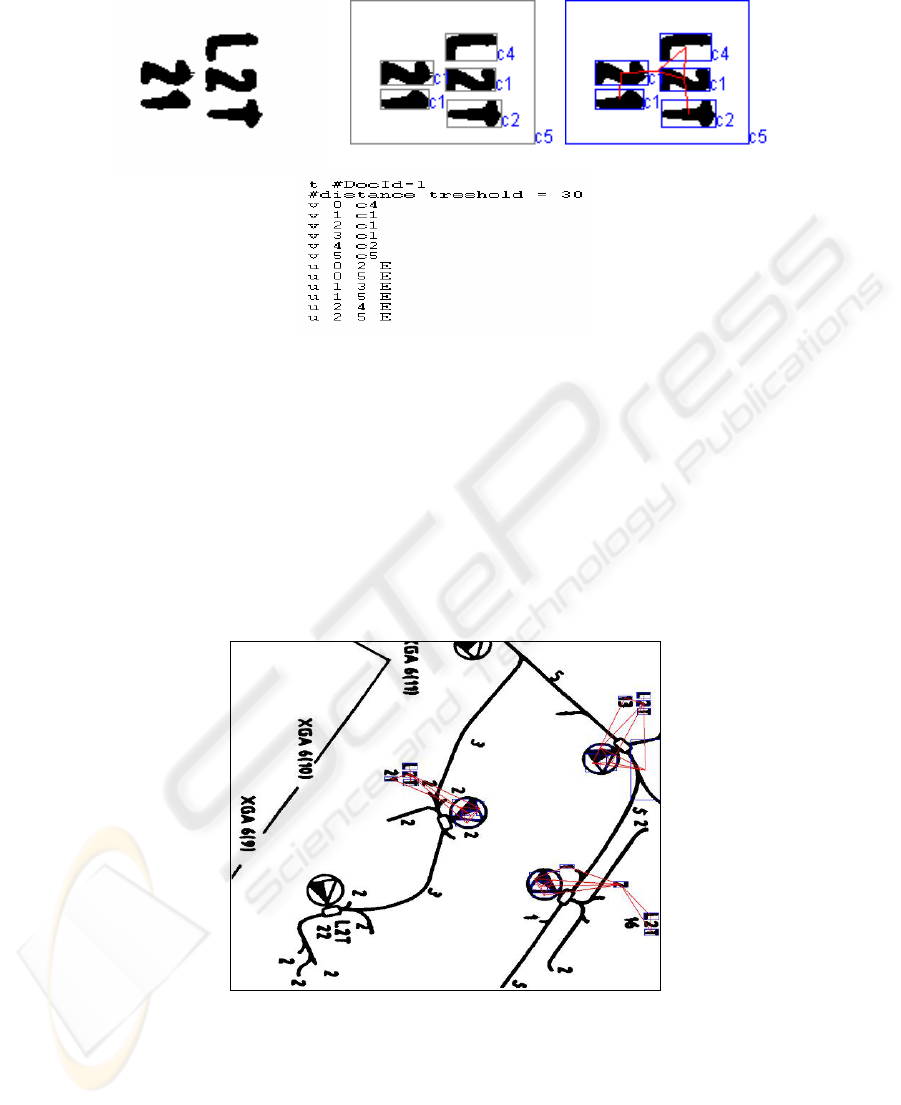
Fig. 2. An image (width=123, height=96) and associated graph transaction

Every connected component of this graph represents a transaction. We can further

simplify the graphs by removing vertices that cannot be frequent and their adjacent

edges. Using FSG we extract the frequent subgraphs and we construct a bag of graphs

occurring in each document. In the following paragraphs we consider that the

frequency condition is sufficient for a group of connected components to form a

symbol and we will conventionally make an equivalence between the frequent

subgraphs found and symbols. As we can see in the example (Fig. 2) the proposed

symbols are far from being perfect due to the image noise, connected components

clustering procedure imperfections, … however we can notice the correlation between

this artificial symbol and the domain symbols.

Fig. 3. Frequent subgraph and its occurences in an image

In conclusion, the subgraphs proposed as frequent are used to model a document

as a bag of symbols. Because some documents may not contain any symbols the

169

document representation is based on two vectors containing connected components

labels, and symbols labels.

()

(

)

....,...,,...,,,,...,,: 2121

mnjjjiii jjjiiissscccA mn

≤

4 Dissimilarity between document descriptions

In this paragraph we present the dissimilarity measure employed between the

documents descriptions that we used.

A collection of documents is represented by a symbol-by-document matrix A,

where each entry represents the occurrences of a symbol in a document image,

, where is the weight of symbol i in document k. Let be the

frequency of symbol i in document k, N the number of documents in the collection,

and

the total number of times symbol i occurs in the whole collection. In this

setting conform with [16] one of the most effective weighting scheme is entropy-

weighting. The weight for symbol i in document k is given by :

)( ika

ika

ikf

))log(

)log(

1(*)1log(

∑

++=

ikik

Now, considering two documents A, B with the associated weights

where t is the total number of symbols, then

),...,,(),,...,,( 2121 tt bbbBaaaA ==

2/1

)(

1),(

∑∑

∑

−=

BAd

represents a dissimilarity measure based on the cosine correlation.

5 Experiments

The corpus used for evaluation contains 60 images from 3 categories: electronic (25

images) and architectural schemas (5 images) and engineering maps (30 images) (see

Fig. 5). In order to present a corpus summary we employed a multidimensional

scaling algorithm to represent in a two dimensional plot the dissimilarities between

documents (see Fig. 4). Each document image is described with one of the following

types of features : Zernike moments for the whole image (a vector with 16

components) or the connected components and symbols lists described above. In Fig.

4.a) we present the dissimilarities between images represented by Zernike moments.

In Fig. 4.b) are plotted the dissimilarities between the document images computed

using the cosine correlation presented in section 4. Each image from the corpus has an

170

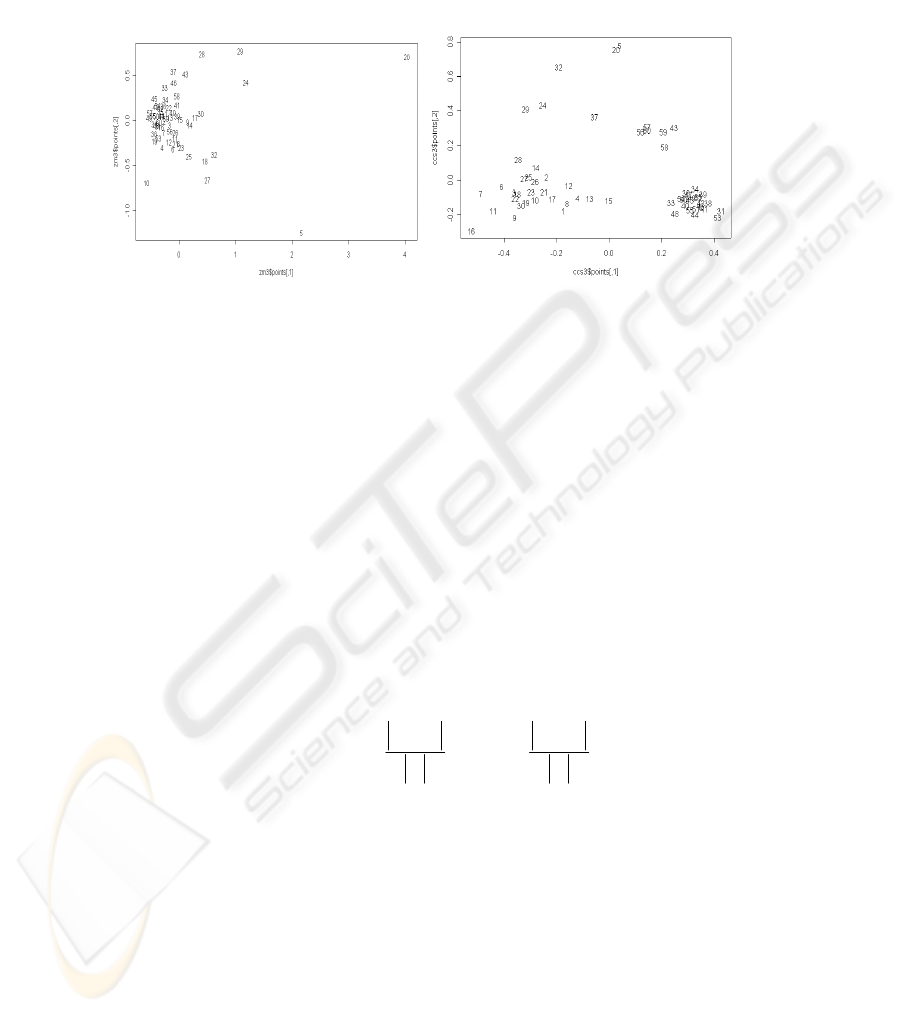
id from 1 to 60. The engineering maps have identifiers from 1 to 30, electronic images

from 31 to 55, and the arhitectural schemas from 56 to 60. We can see in Fig. 6 that

the bag of symbols representation separate better the image classes. This fact has an

important influence on the quality of the query results.

a.) b.)

Fig. 4. Documents ids presented in a two dimensional space with respect to their reciprocal

dissimilarities

A query can be an image, a list of symbols and connected components, or only one of

the later lists.

()

(

)

....,...,,...,,,,...,,: 2121

mnjjjiii jjjiiissscccquery mn

≤

(

)

....,,...,,: 21

mjjj jjjsssquery m

≤

(

)

....,,...,,: 21

niii iiicccquery n

≤

In order to extract the formal description of a given query image we label the

connected components of the query image, construct the graph, and employ graph

matching to detect which symbols occur in the query image. At the end of this process

the query image is described by the two lists of connected components and symbols.

In order to evaluate experimental results we used precision and recall measures. If A

is the set of relevant images for a given query, and B is the set of retrieved images

then :

precision

∩

recall

∩

171

Fig. 5. Corpus images

This corpus contains images that are scanned and contain real and artificial noise.

Table 3. Queries recall and precision

Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10

recall 0.75 0.5 0.48 0.55 0.56 0.76 0.6 0.4 0.32 0.16

precision 0.6 0.31 0.8 0.73 0.87 0.95 0.88 0.5 0.42 0.4

Queries Q1-4 represents symbol queries , i.e. as input is a list of symbols. The