PARTICLE-FILTER APPROACH AND MOTION STRATEGY FOR

COOPERATIVE LOCALIZATION

Fernando Gomez Bravo

Departamento de Ingenier

ıa Electrnica, Sistemas Inform

aticos y Autom

atica

Univ. de Huelva - Spain

Alberto Vale, Maria Isabel Ribeiro

Institute for Systems and Robotics, Instituto Superior T

ecnico

Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal

Keywords:

Particle-Filter, Cooperative Localization, Navigation Strategies.

Abstract:

This paper proposes a Particle-Filter approach and a set of motion strategies to cooperatively localize a team of

three robots. The allocated mission consists on the path following of a closed trajectory and obstacle avoidance

in isolated and unstructured scenarios. The localization methodology required for the correct path following

relies on distance and orientation measurements among the robots and the robots and a ﬁxed active beacon.

Simulation results are presented.

1 INTRODUCTION

This paper proposes a methodology for cooperative

localization of a team of robots based on a Particle-

Filter (PF) approach, relying on distance and orienta-

tion measurements among the robots and among these

and a ﬁxed beacon. It is considered that the ﬁxed bea-

con has sensorial capabilities of range and orientation

measurement, but has a maximum detectable range.

Each robot has limited range detection along a limited

ﬁeld of view. For localization purposes, the proposed

approach propagates a PF for each robot. The parti-

cle weight update is based on the measurements (dis-

tance and orientation) that each robot acquires relative

to the other robots and/or the ﬁxed beacon. A motion

strategy is implemented in such a way that each robot

is able to detect, at a single time instant, at least one

teammate or the ﬁxed beacon. Therefore, either the

ﬁxed beacon (if detected) or the other robots (if de-

tected) play the role of an external landmark for the

localization of each robot.

The developed strategy is targeted to an exploration

mission and it is considered that all the robots start

the mission close to the ﬁxed beacon, evolve in the

environment, eventually may loose detection of the

ﬁxed beacon, and have to return to the starting loca-

tion. Even more, due the sensorial limitations of the

robots they also could loose detection among them.

Cooperative localization is a key component of co-

operative navigation of a team of robots. The use of

multi-robot systems, when compared to a single ro-

bot, has evident advantages in many applications, in

particular there where the spatial or temporal cover-

age of a large area is required. An example on the

scientiﬁc agenda is the planet surface exploration, in

particular Mars exploration. At the actual technol-

ogy stage, the difﬁculty in having human missions to

Mars justiﬁes the development, launching and opera-

tion of robots or teams of robots that may carry out

autonomously or semi-autonomously a set of explo-

ration tasks. The mission outcomes in the case of

surface exploration may largely beneﬁt from having

a team of cooperative robots rather than having a sin-

gle robot or a set of isolated robots. In either case, and

depending on the particular allocated mission, the ro-

bots may have to be localized relative to a ﬁxed bea-

con or landmark, most probably the launcher vehicle

that carried them from earth.

Cooperative localization schemes for teams of ro-

bots explore the decentralized perception that the

team supports to enhance the localization of each ro-

bot. These techniques have been studied in the recent

past, (Gustavi et al., 2005; Tang and Jarvis, 2004; Ge

and Fua, 2005; Martinelli et al., 2005).

In the approach presented in this paper, besides co-

operative localization, the team navigation involves

obstacle avoidance for each robot and a motion strat-

egy where one of the robots, the master, follows a pre-

speciﬁed path and the other teammates, the slaves,

have a constrained motion aimed at having the mas-

ter in a visible detectable range from, at least, one of

the slaves. The master stops whenever it is to loose

Gomez Bravo F., Vale A. and Isabel Ribeiro M. (2006).

PARTICLE-FILTER APPROACH AND MOTION STRATEGY FOR COOPERATIVE LOCALIZATION.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 50-57

DOI: 10.5220/0001203300500057

 SciTePress

visible contact with the slaves and these move to ap-

proach the master and to provide it with visible land-

marks.

The localization problem has to deal with the un-

certainty in the motion and in the observations. Com-

mon techniques of mobile robot localization are based

on probabilistic approaches, that are robust relative to

sensor limitations, sensor noise and environment dy-

namics. Using a probabilistic approach, the localiza-

tion turns into an estimation problem with the evalua-

tion and propagation of a probability density function

(pdf). This problem increases when operating with

more than one robot, with complex sensor’s model or

during long periods of time. A possible solution for

the localization problem is the PF approach, (Thrun

et al., 2001; Rekleitis, 2004), that tracks the variables

of interest. Multiple copies (particles) of the variable

of interest (the localization of each robot) are used,

each one associated with a weight that represents the

quality of that speciﬁc particle.

The major contribution of this paper is the use of

a PF approach to solve the cooperative localization

problem allowing the robots to follow a reference path

in scenarios where no map and no global positioning

systems are available and human intervention is not

possible. The simulation is implemented with a ﬂeet

of three car-like vehicles.

This paper is organized as follows. Section 1

presents the paper motivation and an overview of re-

lated work on mobile robot navigation using PF. Sec-

tion 2 introduces the notation and the principles of

Particle-Filter. Section 3 explains the main contribu-

tions of the paper, namely the cooperative localiza-

tion and motion strategy using PF in a team of ro-

bots. Simulation results obtained with some robots in

an environment with obstacles are presented in Sec-

tion 4. Section 5 concludes the paper and presents

directions for further work.

2 SINGLE ROBOT NAVIGATION

This section describe the robots used in the work and

presents the basis for the PF localization approach

for each single robot in the particular application de-

scribed in Section 1.

2.1 Robot Characterization

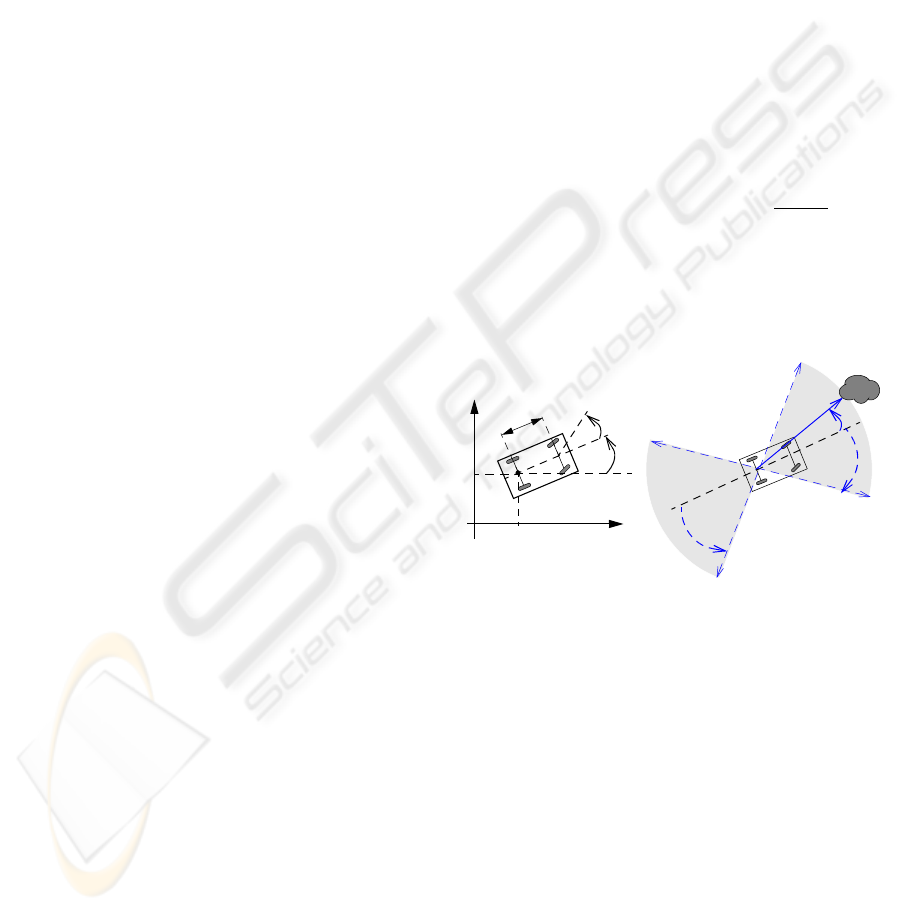
It is assumed that each robot is equipped with a

2D laser scanner, with a maximum range capability,

max

, over a limited rear and front angular ﬁeld of

view of width 2ϕ

max

, as represented in Figure 1-

right. Consequently, the robots are able to measure

the distance, ρ, and the direction, ϕ, to obstacles in

their close vicinity and are prepared to avoid obsta-

cles. This sensor supports the robot perception to

evaluated the distance and the orientation under which

the beacons (the ﬁxed beacon and/or the other robots

in the team) are detected. It is also assumed that each

robot is able to recognize the other robots and the

ﬁxed beacon based on the same laser scanner or us-

ing, for instance, a vision system.

Maneuvering car/cart-like vehicles is a difﬁcult

task, when compared with other type of vehicles,

for instance mobile robots with differential kinematic

system. Due to this fact, car/cart-like kinematic sys-

tem has been considered to emphasize the capabilities

of the purposed localization technique when applied

on these type of vehicles. The kinematic model of

a car/cart-like vehicle, presented in Figure 1, is ex-

pressed by





˙x

˙y





cos(θ) 0

sin(θ) 0

0 1



v(t)

tan φ(t)



(1)

where (x, y) is the position, θ is the vehicle’s heading,

both relative to a global referential, v(t) is the linear

velocity and φ(t) is the steering angle that deﬁnes the

curvature of the path and l is the distance between the

rear and front wheels (see Figure 1-left).

x

max

Figure 1: Robot’s kinematic model (left) and sensorial ca-

pabilities (right).

The proposed navigation strategy is optimized for

car/cart like vehicles (as described in Section 3), but

the approach can be implemented in robots with sim-

ilar capabilities of motion and perception.

2.2 Localization Based on

Particle-Filter

The pose of a single robot is estimated based on a

PF, (Thrun et al., 2001). Each particle i in the ﬁlter

represents a possible pose of the robot, i.e.,

p =





. (2)

In each time interval, a set of possible poses (the

cloud of particles) is obtained. Then, the particles are

classiﬁed according to the measurement obtained by

PARTICLE-FILTER APPROACH AND MOTION STRATEGY FOR COOPERATIVE LOCALIZATION

the robot at its real pose. Simulations of the measure-

ments are performed, considering each particle as the

actual pose of the robot and the probabilistic model

of the sensor. The believe of each particle being the

real pose of the robot is evaluated taking into account

these measurements. The real pose of the robot is es-

timated by the average of the cloud of particles based

on their associated believes. An important step of

the method is the re-sampling procedure, where the

less probable particles are removed from the cloud,

bounding the uncertainty of the robot pose, (Rekleitis,

2004).

Differently from other approaches, where a set

of ﬁxed beacons are distributed for localization pur-

poses, (Betke and Gurvits, 1997), this paper considers

the existence of a single ﬁxed beacon L at (x

, y

as represented in Figure 2- a, that provides a ﬁxed ref-

erence each time the robot observes it. The ﬁxed bea-

con has sensorial capabilities similar to those of the

robots, with limited range detection but over a 360

◦

ﬁeld of view (see Figure 2-a).

,,()

Cloud of particles

Figure 2: a) Robot and a ﬁxed beacon observation and b)

each particle and robot observations.

The particles associated to the robot are weighted

taking into account the observations made by the ro-

bot and by the ﬁxed beacon. Let ρ

and ϕ

be the

distance and the relative orientation of the robot B ob-

tained from the ﬁxed beacon measurement (Figure 2-

a). Similarly, ρ

and ϕ

are the distance and the

relative orientation of the beacon obtained from the

robot measurement (Figure 2-b). Additionally, each

particle associated to the robot B deﬁnes

and

(which represents the ﬁxed beacon measure-

ment if the robot was placed over the particle i):

−

)

+ (y

−

)

+ ξ

(3)

= arctan





+ ξ

(4)

where ξ

and ξ

represent the range and angular un-

certainties of the laser sensor, considered as Gaussian,

zero mean, random variables. The simulated mea-

surements for each particle deﬁne two weights,

and

, related to the acquired sensorial data as,

= κ



−



−1

(5)

= κ



−



−1

(6)

where κ

and κ

are coefﬁcients that allow to com-

pare both distances. Thus, a weight that determines

the quality of each particle according to the beacon

measurement is given by



if V

= 1

1 if V

= 0

(7)

where η

is a normalization factor and V

is a

logic variable whose value is 1 if L observes B, and 0

otherwise. On the other hand, each particle also de-

ﬁnes

(which represents the robot mea-

surement of the distance and angle with which the

ﬁxed beacon will be detected if the robot were placed

over the particle i, i.e., in

B, see Figure 2-b) and V

(a logic variable whose value is 1 if B observes L and

0 otherwise). The weight that determines the quality

of each particle according to the measurement to the

beacon is similar to (7), by switching the indices “B”

and “L”. Therefore, the total weight of the particle i

associated with the robot B,

, is given by

(8)

where

is a normalization factor. Given the for-

mulation of the weights, if the vehicle is not able to

observe the ﬁxed beacon and the ﬁxed beacon is not

able to detect the robot, or equivalently V

= 0

and V

= 0, all the particles have the same im-

portance. As will be shown in Section 4, when no

observations are available, re-sampling is not possi-

ble and therefore localization uncertainty increases.

Once the mobile robot observes again the ﬁxed bea-

con or vice-versa, re-sampling is possible and uncer-

tainty decreases.

ICINCO 2006 - ROBOTICS AND AUTOMATION

2.3 Path Following and Obstacle

Avoidance

Due to the limited range of perception featured by

the sensors, the robot may navigate in areas where

the perception of the ﬁxed beacon is not available.

To cope with this constraint the navigation strategy

should assure that the vehicle will return to the ini-

tial conﬁguration, i.e., the initial position where the

vehicle and the beacon are able to detect each other.

Different strategies can be applied to drive the robot

to the initial conﬁguration.

One strategy is based on a set of way points along

a closed path. However, the environment is still un-

known and some way points could lay over an obsta-

cle. When this occurs the navigation algorithm may

endows to an unreachable point leading to circular

paths around obstacles. To overcome this problem

another strategy is adopted. The idea is to build a

continuous path that the robot has to follow with an

obstacle avoidance capability based on reactive navi-

gation techniques.

Different approaches have been proposed for path

following, where the robot position is estimated by

Extended Kalman Filter (EKF) using Global Position

System (GPS) and odometry (Grewal and Andrews,

1993). In the present work no GPS is available, and

rather than using EKF, a PF approach is used.

To accomplish an accurate navigation, each ro-

bot follows a path previously deﬁned and the “Pure-

pursuit” algorithm (Cuesta and Ollero, 2005) is ap-

plied for path-tracking. This algorithm chooses the

value of the steering angle as a function of the esti-

mated pose at each time instant. Without a previous

map, different obstacles may lay over the path and,

consequently, a reactive control algorithm will be ap-

plied if the vehicle is near an obstacle, (Cuesta et al.,

2003). The path-tracking and the obstacle avoidance

are combined in such a way that the robot is able

to avoid the obstacle and continue the path-tracking

when the vehicle is near the path.

3 COOPERATIVE

LOCALIZATION AND

NAVIGATION

This section illustrates the cooperation among robots

to improve the robots localization when the detec-

tion of the ﬁxed beacon is not available. The method

takes advantage of the measurement of the different

teammates in order to estimate the pose of each robot.

Moreover, a cooperative motion strategy is presented

that allows the team of robots to perform a more efﬁ-

cient localization. Robots are identiﬁed by numbers 1

to 3 and the ﬁxed beacon is numbered with 4 as rep-

resented in Figure 3.

3.1 Cooperative Robots Localization

Based on Particle-Filter

The pose of each robot is estimated by the PF tech-

nique, considering all the robots involved, i.e., the

measurements acquired by all the robots. When a ro-

bot moves, only the weights of the particles of that

robot are updated. However, the estimation of the po-

sition using PF is performed taking into account the

measurements acquired by the sensors of that robot

and the other robots.

Similarly for the case involving the ﬁxed beacon, if

B is a robot moving and A is a static robot, the obser-

vation of robot B performed by the robot A deﬁnes the

values ρ

and φ

. In the same way, the observa-

tion of robot A performed by robot B deﬁnes ρ

and

, which is similar to Figure 2, replacing the bea-

con L by the robot A. Thus, each particle associated

with the robot B deﬁnes the values

and

. These values can be obtained applying ex-

pressions similar to (3) and (4). Nevertheless, in this

case, instead of using the position of the ﬁxes beacon,

the estimated position of the robot A (ˆx

, ˆy

) is

considered. Therefore, from the measurement of ro-

bot A and B, the weights

and

, which de-

termine the quality of each particle according to both

measurements, can be obtained. The weights are cal-

culated by expressions similar to (5), (6) and (7).

Therefore, all the measurements acquired by a ro-

bot depend on the estimated position of the other ro-

bots. The evaluation for the poses estimation includes

cumulative errors and, consequently, the weight of the

particles are inﬂuenced by the measurement provided

by the ﬁxed beacon (when it is able to observe the

robots or the robots are able to observe the ﬁxed bea-

con). Then, the weight of the particle i of the robot j

is given by



n=1,n6=j

if V

+ V

= 0

if V

+ V

= 1

whose value depends on the logic variables V

(equal

to 1 if the robot j can observe the ﬁxed beacon) and

(equal to 1 if the ﬁxed beacon is able to observe

the robot j).

3.2 Motion Strategy

In this approach, the objective of the team naviga-

tion is the exploration of an unknown environment.

A closed path is deﬁned to be followed by one of the

robots of the team. For a correct path following, local-

ization is carried out using the PF approach described

in sections 2.1 and 2.2. As the path may be such that

PARTICLE-FILTER APPROACH AND MOTION STRATEGY FOR COOPERATIVE LOCALIZATION

the ﬁxed beacon is not detected, to achieve this goal

some robots operate as beacons to their teammates,

with this role interchanged among them according to

a given motion strategy.

There are other approaches exploring the same

idea. In (Grabowski and Khosla, 2001; Navarro-

Serment et al., 2002) a team of Milibots is organized

in such a way that part of the team remains station-

ary providing known reference points for the moving

robots. This approach, named as “leap-frogging” be-

haviour, uses trilateration to determine the robots po-

sition. To apply trilateration, three beacons are re-

quired. During the main part of the navigation prob-

lem considered in this paper, only two robots (acting

as beacons) are detected from the robot whose local-

ization is under evaluation, as the ﬁxed beacon is not

detected. There are situations where only a single ro-

bot is visible and trilateration is not useful.

In (Rekleitis, 2004) a collaborative exploration

strategy is applied to a team of two robots where one

is stationary, and acts as a beacon, while the other is

moving, switching the roles between them. In that

approach, PF technique is applied for cooperative lo-

calization and mapping. Nevertheless, it is supposed

that the heading of the observed robot can be mea-

sured. Since this estimation is not trivial, this paper

presents a different approach for PF.

In the proposed methodology the team is divided

in two categories of robots. One of the robots is con-

sidered the “master” having the responsibility of per-

forming an accurate path following of a previously

planned trajectory. The other two robots, the “slaves”,

play the role of mobile beacons. The master robot is

identiﬁed by the number 1, and the slave robots with 2

and 3 (see Figure 3). Initially, the master follows the

planned path until it is not able to detect, at least, one

slave. Once this occurs, the master stops and the slave

robots start to navigate sequentially. They try to reach

different poses where they will act as a beacon for the

master. These poses can be determined previously,

taking into account the path and a criterion of good

coverage, or can be established during the navigation,

considering the position where the master stopped. In

both cases, the objective is to “illuminate” the master

navigation by the slave mobile beacons in such a way

that it can be located accurately. At this stage, once

the master stops and one of the slaves is moving, the

master and the other slave play the role of beacon for

the slave which is moving.

According to the previous statement and consider-

ing the type of sensors and the angular ﬁeld of view, a

strategy for motion of the slaves is considered. The

strategy is based on the idea of building a triangu-

lar formation after the master stops, what happens

when the master is not able to detect, at least, one

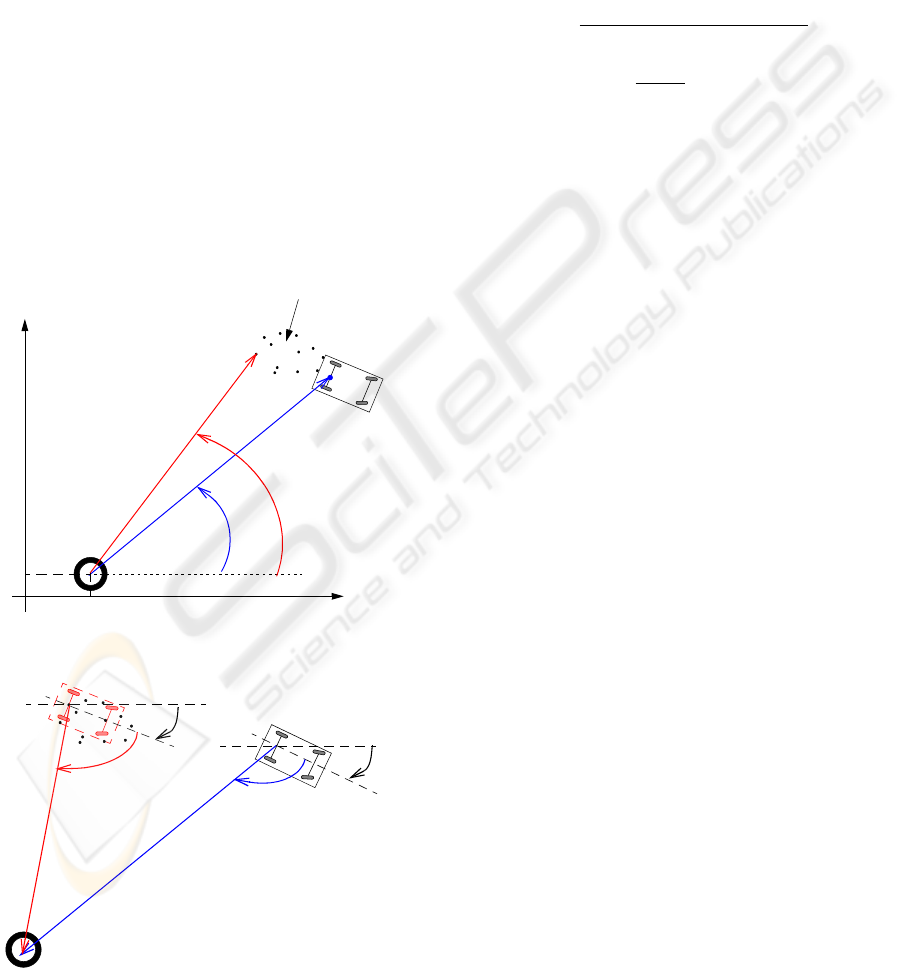
slave. Using this triangular conﬁguration the vehicles

are allowed to estimate their position by means of the

Beacon

Slave

Master

Figure 3: β-spline generation.

measurement of their relative positions with the min-

imum possible error. Furthermore, slave robots give

the master a large position estimation coverage. This

conﬁguration is fundamental if the view angle of the

sensors is constrained, otherwise, the robots can see

each other in any conﬁguration.

Once the master has stopped, two points P

and P

are generated (see Figure 3) and the slaves will have

to reach these points with the same orientation of the

master so that they can see each other. P

and P

are

calculated by taking into account the angular ﬁeld of

view of the robots. Hence, P

is located along the

master’s longitude axis and P

is such that the master,

and P

deﬁne an isosceles triangle.

Therefore, when the master robot stops, a path is

generated in such a way that it connects each current

slave position with the goal point (P

or P

). This

path has also to accomplish the curvature constraint

and allow the slave vehicles to reach the goal point

with a correct orientation. For this purpose, β-Splines

curves, (Barsky, 1987), have been applied as repre-

sented in Figure 3.

Master and slave perform the path following and

the collision avoidance in a sequential way. The slave

2 starts moving when the master has stopped. The

slave 3 begins to move once the slave 2 reaches its

goal. Finally, the master starts moving when the slave

3 has reached its target conﬁguration.

4 SIMULATION RESULTS

Different experiments have been implemented to test

the proposed approach, performed with different

numbers of teammate: one, two and three robots.

Several trajectories have been generated to evaluate

the inﬂuence of the length and the shape of the path

on the localization performance.

The algorithm was tested by considering that the

robots perform both clockwise or anti-clockwise

loops. Figure 4-a) presents the desired path (dotted-

line), the real path (continuous line) and the estimated

path (dashed-line) obtained by the navigation of a sin-

gle robot, i.e., no cooperative localization is consid-

ered. The ﬁxed beacon is represented by the non-

ICINCO 2006 - ROBOTICS AND AUTOMATION

ﬁlled circle. Figure 4-b) presents the evolution of the

cloud of particles along the navigation process, which

conveys the associated uncertainty. The cloud shrinks

when the robot observes the ﬁxed beacon and enlarges

when no observation is acquired.

Figure 4: a) Single robot navigation and b) evolution of the

cloud of particles.

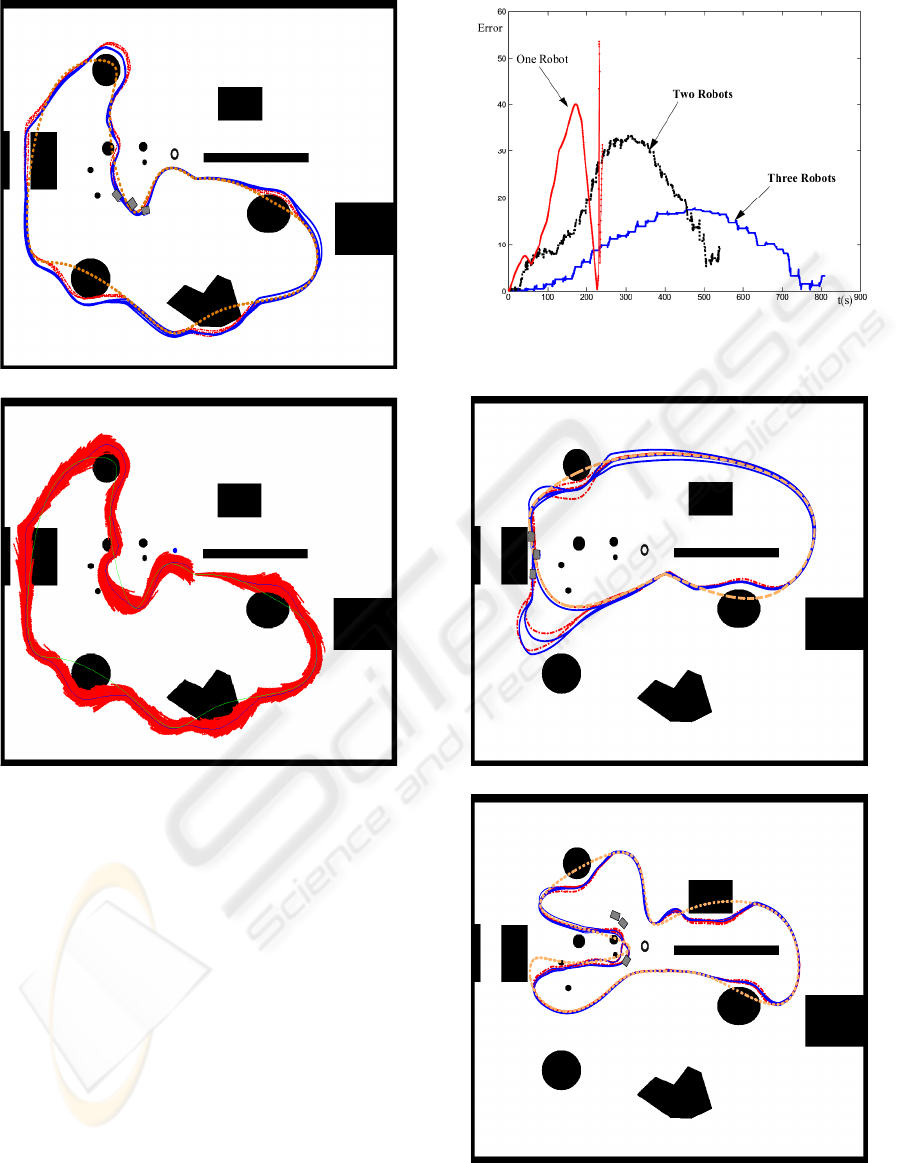
Figures 5-a) and 6-a) illustrate the evolution of the

real and the estimated path when the cooperative nav-

igation is applied on a team of two and three robots,

respectively, along the same desired path. Figures 5-

b) and 6-b) present the evolution of the cloud of parti-

cles for the master robot. The estimation is improved,

mainly when using three robots and, consequently,

the navigation of the master robot is closer to the de-

sired path. In each experiment the robots closed the

loop three times. The improvement in the pose es-

timation when applying the cooperative localization

technique is shown in these ﬁgures as the real and the

estimated path are closer than in the previous experi-

ment, with a single robot.

SLAVE

Figure 5: a) Two ro bots in a big loop and b) evolution of the

cloud of the master robot.

Figure 7 presents the error of the position estima-

tion in the previous three experiments along one loop,

with different number of teammate. It is remarkable

that the error decreases when the number of the robots

in a team increases. However, the time the robots take

to close the loop increases with the number of team-

mate, since the motion strategy for cooperative local-

ization requires that part of the team remain stationary

while one of the robot is navigating.

Figure 8 illustrates two experiments with different

paths in which a team of three robots closed the loop

several times. Both paths are shorter than the path of

Figure 5-a). In the path of Figure 8-b) (the one whose

shape looks like a Daisy) the robots navigate close to

the beacon for three times.

PARTICLE-FILTER APPROACH AND MOTION STRATEGY FOR COOPERATIVE LOCALIZATION

MASTER

SLAVE 2

SLAVE 3

Figure 6: a) Three robots in a big loop and b) evolution of

the cloud of the master robot.

Figure 9 presents the error of the position estima-

tion along one loop of the experiment of Figure 8-

a),b) and 5-a). It illustrates that shorter paths provide

lower error and therefore better performance. In ad-

dition, this ﬁgure also illustrates that the pose estima-

tion can be improved by modifying the shape of the

path as is the case of the experiment of the ”Daisy

path (Figure 8-b). In this experiment, the error re-

mains bounded presenting lower values than the other

experiments. This improvement is achieved due to the

effect of navigating near the beacon and applying its

perception for updating the weight of the robots par-

ticles. Obviously, the pose estimation improves when

the time periods where the robot navigates near the

beacon increases. A conclusion is, if the exploration

of wide and large spaces is needed, trajectories similar

Figure 7: Position estimation error along the big loop for

teams with 1, 2 and 3 robots.

MASTER

SLAVE 2

SLAVE 3

MASTER

SLAVE 2

SLAVE 3

Figure 8: Cooperative navigation along two different p aths:

a) short loop and b) Daisy loop.

ICINCO 2006 - ROBOTICS AND AUTOMATION

Figure 9: Position estimation error along one loop for a

team of three robots along different paths.

to the daisy path are preferred, i.e., trajectories where

the team navigates near the beacon several times.

5 CONCLUSION AND OPEN

ISSUES

This paper presented a Particle-Filter approach to

solve the cooperative localization problem for a small

ﬂeet of car-like vehicles in scenarios without map or

GPS and no human intervention. A team of three ro-

bots and a ﬁxed beacon have been considered in such

a way that the robots take advantage of cooperative

techniques for both localization and navigation. Each

robot serves as an active beacon to the others, working

as a ﬁxed reference and, at the same time, providing

observations to the robot which is moving. With this

approach, robots are able to follow a previous calcu-

lated path and avoid collision with unexpected obsta-

cles.

Moreover, the proposed approach has been vali-

dated by different simulated experiments. Different

path and number of teammates have been considered.

The experiments illustrate that the number of team-

mates decreases the estimation error. Likewise, the

length of the planned path affects to the quality of the

estimation process. However, for paths with similar

length, the estimation procedure can be improved by

changing its shape.

The following step is the implementation of this ap-

proach in a team of real car-like robots. There are still

open issues requiring further research, in particular

the number of particles and other tuning parameters,

the matching between beacons and other mobile ro-

bots and the implementation of active beacons.

ACKNOWLEDGEMENTS

Work partially supported by the Autonomous Gover-

ment of Andalucia and the Portuguese Science and

Technology Foundation (FCT) under Programa Op-

eracional Sociedade do Conhecimento (POS C) in the

frame of QCA III. First author also acknowledges the

support received by the ISR.

REFERENCES

Barsky, B. (1987). Computer graphics and geometric mod-

elling using β-Splines. S.-Verlag.

Betke, M. and Gurvits, L. (1997). Mobile robot localization

using landmarks. IEEE Transaction on Robotics and

Automation, 13(2):251 – 263.

Cuesta, F. and Ollero, A. (2005). Intelligent Mobile Robot

Navigation. Springer.

Cuesta, F., Ollero, A., Arrue, B., and Braunstingl, R.

(2003). Intelligent control of nonholonomic mobile

robots with fuzzy perception. Fuzzy Set and Systems,

134:47 – 64.

Ge, S. S. and Fua, C.-H. (2005). Complete multi-robot

coverage of unknown environments with minimum re-

peated coverage. Proc. of the 2005 IEEE ICRA, pages

727 – 732.

Grabowski, R. and Khosla, P. (2001). Localization tech-

niques for a team of small robots. Proc. of the

IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems, 2:1067 – 1072.

Grewal, M. S. and Andrews, A. P. (1993). Kalman Filtering

Theory and Practice. Prentice-Hall, Englewood Cliffs

and New Jersey.

Gustavi, T., Hu, X., and Karasalo, M. (2005). Multi-robot

formation control and terrain servoing with limited

sensor information. Preprints of the 16th IFAC World

Congress.

Martinelli, A., Pont, F., and Siegwart, R. (2005). Multi-

robot localization using relative observations. Proc. of

the 2005 IEEE Int. Conf. on Robotics and Automation,

pages 2808 – 2813.

Navarro-Serment, L. E., Grabowski, R., Paredis, C., and

Khosla, P. (2002). Localization techniques for a team

of small robots. IEEE Rob. and Aut. Magazine, 9:31 –

40.

Rekleitis, I. (2004). A particle ﬁlter tutorial for mobile robot

localization. (TR-CIM-04-02).

Tang, K. W. and Jarvis, R. A. (2004). An evolutionary com-

puting approach to generating useful and robust ro-

bot team behaviours. Proc. of 2004 IEEE/RSJ IROS,

2:2081 – 2086.

Thrun, S., Fox, D., Burgard, W., and Murphy, F. D. (2001).

Robust monte carlo localization for mobile robot. Ar-

tiﬁcial Intelligence Magazine, 128(1 - 2):99 – 141.

PARTICLE-FILTER APPROACH AND MOTION STRATEGY FOR COOPERATIVE LOCALIZATION