BAYESIAN ESTIMATION OF DISTRIBUTED PHENOMENA

USING DISCRETIZED REPRESENTATIONS OF

PARTIAL DIFFERENTIAL EQUATIONS

Felix Sawo, Kathrin Roberts and Uwe D. Hanebeck

Intelligent Sensor-Actuator-Systems Laboratory

Institute of Computer Science and Engineering

Universit

at Karlsruhe (TH)

Karlsruhe, Germany

Keywords:

Stochastic systems, Baysian estimation, model-based reconstruction, distributed phenomenon, environmental

monitoring, sensor-actuator-network.

Abstract:

This paper addresses a systematic method for the reconstruction and the prediction of a distributed phenom-

enon characterized by partial differential equations, which is monitored by a sensor network. In the ﬁrst step,

the inﬁnite-dimensional partial differential equation, i.e. distributed-parameter system, is spatially and tempo-

rally decomposed leading to a ﬁnite-dimensional state space form. In the next step, the state of the resulting

lumped-parameter system, which provides an approximation of the solution of the underlying partial differen-

tial equations, is dynamically estimated under consideration of uncertainties both occurring in the system and

arising from noisy measurements. By using the estimation results, several additional tasks can be achieved

by the sensor network, e.g. optimal sensor placement, optimal scheduling, and model improvement. The

performance of the proposed model-based reconstruction method is demonstrated by means of simulations.

1 INTRODUCTION

Recent developments in wireless sensor network tech-

nology and miniaturization of sensor nodes make it

possible to exploit centralized (Kumar et al., 2002)

and decentralized (Rao et al., 1993) sensor networks

for monitoring the natural environment (Thuraising-

ham, 2004; Culler and Mulder, 2004). Such sensor

networks can be used for example in industrial, med-

ical, urban, and many other environments. Further-

more, applying sensor networks can provide new data

for environmental science, such as climate models, as

well as growth and reproduction of coral reef indi-

cated by physical environmental factors, e.g. temper-

ature, water movement, salt concentration, and pollu-

tant concentration. Further examples are reconstruc-

tion of ﬂuid-ﬂow in a thermal reactor (Faulds and

King, 2000), and reconstruction of the surface mo-

tion of a beating heart in minimally invasive surgery

(Ortmaier et al., 2005).

In practical implementations the sensor nodes are

normally densely deployed either inside the phenom-

enon or very close to it. In order to get meaningful in-

formation not only at the sensor nodes itself but also

between these nodes, the reconstruction of the distrib-

uted phenomenon is of major signiﬁcance.

For the prediction of the state of such phenomenon

we present a new method for systematic data process-

ing. Basically, data from the sensor network in form

of measurement results as well as data from a physical

model are used to derive the best possible estimate for

the state of a distributed phenomenon; even at non-

measurement points. The estimation results on the

other hand can be used for ﬁnding the optimal place-

ment and measurement time sequences for the sensor

nodes, or for improving the parameter values of the

used physical model, see Fig. 1.

However, for a model-based approach it is neces-

sary to solve the partial differential equations char-

acterizing the distributed phenomena. Such equa-

tions can be solved for example by the ﬁnite-element

method or the ﬁnite-difference method (Baker, 1983).

The unstructured nature of those methods permits a

good geometrical description of complex geometries.

Additionally, it is possible to solve even nonlinear

partial differential equations. However, many para-

meters describing uniquely the state of the distrib-

uted phenomenon are necessary to achieve appropri-

ate convergence.

On the other hand, there are modal analysis meth-

ods using a set of global expansion functions. These

methods just need a few parameters for characterizing

Sawo F., Roberts K. and D. Hanebeck U. (2006).

BAYESIAN ESTIMATION OF DISTRIBUTED PHENOMENA USING DISCRETIZED REPRESENTATIONS OF PARTIAL DIFFERENTIAL EQUATIONS.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 16-23

DOI: 10.5220/0001203800160023

 SciTePress

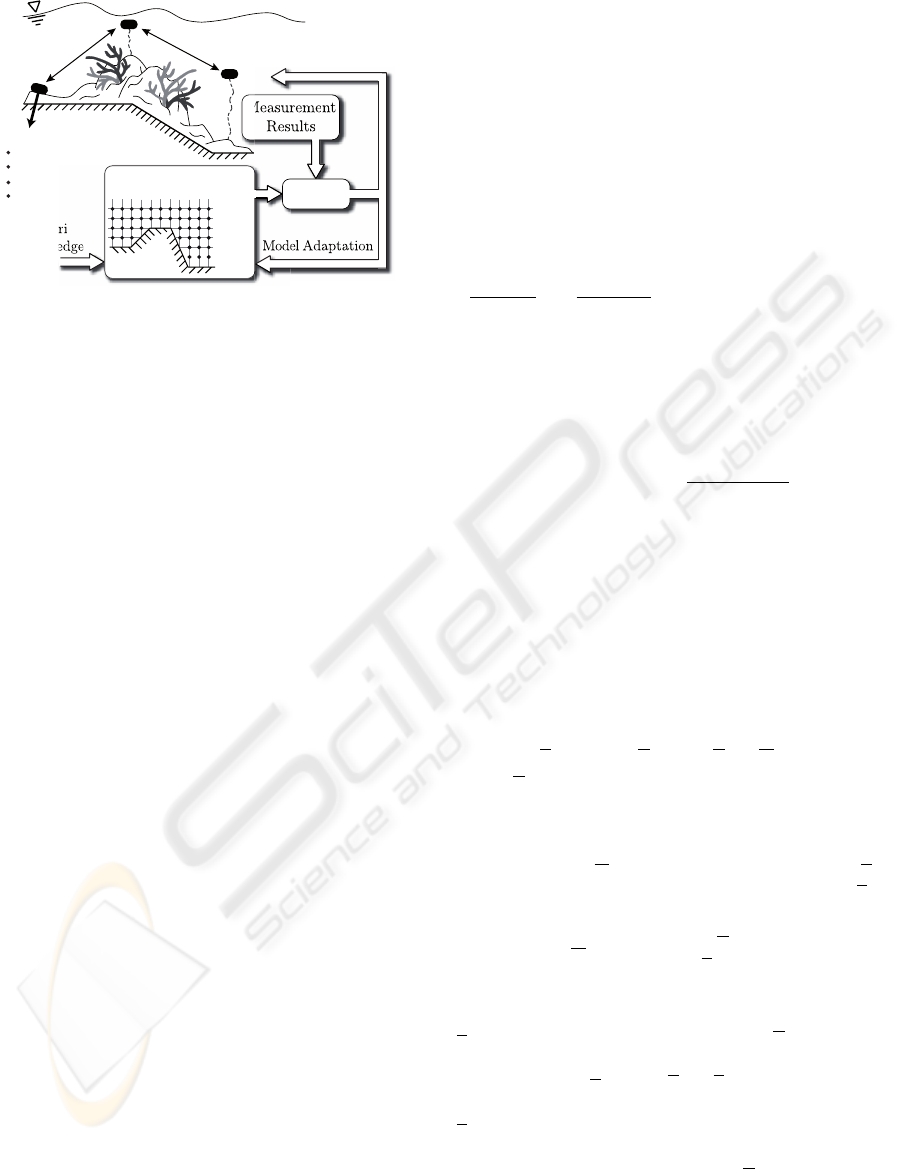
Measurement

Results

Model Adaptation

A Priori

Knowledge

Stochastic Model

Fusion

Sensor node:

temperature

salt concen

tration

velocity

pressure

Sensor Scheduling and

Sensor Placement

Figure 1: Visionary scenario for the reconstruction and the

observation of a distributed phenomenon by means of a sen-

sor network; observation of a coral reef.

a smooth solution of the partial differential equation

(Roberts and Hanebeck, 2005). The drawback, how-

ever, is that the modal analysis works only for lin-

ear partial differential equations and global expansion

functions can be found only for problems with simple

boundary conditions.

Combining these two general approaches, leads to

the so-called ﬁnite-spectral method (Karniadakis and

Sherwin, 2005; Fournier et al., 2004; Levin et al.,

2000). Basically, this method approximates the so-

lution within each element with a set of orthogonal

polynomials, such as Legendre, or Chebyshev. Thus,

it combines the geometrical ﬂexibility of conventional

ﬁnite-element methods with the exponential conver-

gence rate associated with the modal analysis.

The novelty of this paper is the model-based ob-

servation of distributed phenomena by a sensor net-

work under consideration of uncertainties both occur-

ing in the physical model, i.e., system model, and

arising from noisy measurements. Here, we extend

and generalize our previous research work (Roberts

and Hanebeck, 2005) in such a way that both the sys-

tem model and the measurement model are derived by

the ﬁnite-spectral method. Using this method, it turns

out that nonlinear phenomena with complex bound-

ary conditions can be reconstructed and predicted in a

systematic manner.

The remainder of this paper is organized as follows.

In Section II, a rigorous formulation of the problem

of the reconstruction of distributed phenomena char-

acterized by partial differential equations is given. In

Section III and IV, the spatial and temporal decom-

position of the partial differential equation is shown.

Finally, in Section V the centralized estimator is de-

rived and its performance is demonstrated by means

of some simulation results; reconstruction of the tem-

perature distribution in a heat rod by means of a sen-

sor network.

2 PROBLEM FORMULATION

The main goal is to design a dynamic system model

for the purpose of estimating the state of a distrib-

uted phenomenon monitored by a sensor network. A

large number of distributed phenomena, such as irro-

tational ﬂuid ﬂow, heat conduction, and wave prop-

agation (Roberts and Hanebeck, 2005), can be de-

scribed by means of a set of linear partial differential

equations.

In this paper, a one-dimensional partial differential

equation is used for simplicity, given by

∂f(z, t)

∂t

− c

∂

f(z, t)

∂z

− s(z, t) = L(f) = 0 , (1)

where f (z, t) denotes the solution of the partial differ-

ential equation, e.g. temperature at a certain location

z and at a certain time t, s(z, t) represents the source

term, and c is a positive constant. Considering the so-

lution in a domain Ω = {z | 0 ≤ z ≤ L}, we assume

following boundary conditions

f(z = L, t) = g

∂f(z = 0, t)

∂z

= g

where g

is referred to as a Dirichlet boundary condi-

tion and g

, specifying a condition on the derivative,

is the so-called Neumann boundary condition.

The above mentioned partial differential equation

(1) describes the distributed phenomenon in an in-

ﬁnite-dimensional state space. However, in order

to estimate and reconstruct the state of a distributed

phenomenon by means of a Bayesian estimation ap-

proach, the partial differential equation has to be char-

acterized by a ﬁnite state space form according to

k+1

= A

+ B

+ w

, (2)

where x

contains the individual states characteriz-

ing the time evolution of the distributed phenomenon

and the matrix A

maps the current state vector at

time step k to the next state vector at time step k + 1.

The noise vector w

contains both driving input ∆u

noises and subsumed endogenous uncertainties d

e.g. modeling errors, according to

= [

I I

]



B∆u



where I is the identity matrix.

Furthermore, it is assumed that the measurements

ˆy

are related linearly to the state vector x

, according

ˆy

= H

+ v

, (3)

where H

denotes the measurement gain matrix and

represents the measurement uncertainties.

Once the system equation and the measurement

equation is derived, the state vector x

characterizing

the distributed phenomena can be estimated by means

of the Kalman ﬁlter for the linear case (Anderson and

Moore, 1979), or nonlinear estimation procedures for

the nonlinear case, e.g. (Hanebeck et al., 2003).

BAYESIAN ESTIMATION OF DISTRIBUTED PHENOMENA USING DISCRETIZED REPRESENTATIONS OF

PARTIAL DIFFERENTIAL EQUATIONS

3 SPATIAL DECOMPOSITION

(ODE-SYSTEM)

In this section we present the spatial decomposi-

tion allowing the conversion of the partial differen-

tial equation (1) into a set of ordinary differential

equations (ODE-System). It is well-known that the

ﬁnite-difference, the ﬁnite-element, and the ﬁnite-

spectral method may be used with the same numerical

methodologies described in the next section, namely

the Galerkin formulation (Baker, 1983; Karniadakis

and Sherwin, 2005).

3.1 Galerkin Formulation

The ﬁrst basic ingredient of a spatial decomposition

method is an approximate solution replacing the inﬁ-

nite expansion by a ﬁnite representation. Thus, it is

assumed that the solution f (z, t) can be represented

by a piecewise approximation

f(z, t) according to

f(z, t) =

dof

−1

i=0

(z) α

(t) , (4)

where Ψ

(z) are analytic functions called the shape

functions, e.g. see Fig. 2 (b), and N

dof

denotes the

degree of freedom of the resulting system description.

The essence of all spatial decomposition methods

such as the ﬁnite-difference, the ﬁnite-element, and

the ﬁnite-spectral method lies in the choice of the

shape functions Ψ

(z). This function is to be spec-

iﬁed in more detail later.

Due to the fact that such approximated solution

cannot satisfy the partial differential equation (1)

everywhere in the region of interest a residual is left.

A common method known as the Galerkin formula-

tion is based on ﬁnding a way to make this resid-

ual small in some sense; achieved by minimizing

an appropriate number of weighted integrals. The

most popular choice for the weighting functions is

the shape function itself. Replacing both the solution

function f (z, t) and the input function s(z, t) by a ﬁ-

nite expansion (4), denoted by

f(z, t) and ˜s(z, t), re-

spectively, leads to following weighted integral over

the solution domain Ω

Ω

(z)

∂

f(z, t)

∂t

− c

∂

f(z, t)

∂z

− ˜s(z, t)

dz = 0

(5)

It can be stated that the minimization of this integral

automatically leads to the best numerical approxima-

tion of the solution f(z, t) of the partial differential

equation (Baker, 1983).

Then, the integral of (5) can be recasted by using

the rules of product differentiation. Applying the fun-

damental theorem of calculus for the evaluation of the

(b)

(a)

Global bases (shape functions)

(z)

f(z, t)

(t)

Figure 2: The solution f(z, t) of the partial differential

equation is approximated by

f(z, t) depending on the shape

functions Ψ

(z) and their weighting coefﬁcients α

(t). (a)

Elemental decomposition of the solution domain Ω into sev-

eral subdomains Ω

. (b) Shape functions Ψ

(z) for the lin-

ear case.

resulting integral leads to

Ω

(z)

∂

f(z, t)

∂t

dz =

Ω

(z)˜s(z, t)dz (6)

− c

Ω

dΨ

(z)

∂

f(z, t)

∂z

dz + c

(z)

∂

f(z, t)

∂z

∂Ω

where the last term on the right-hand side contains the

boundary conditions, i.e., ∂Ω

and ∂Ω

denotes the

right-hand and left-hand boundary, respectively. This

weighted residual statement is known as the weak for-

mulation of the partial differential equation (1).

As it is shown in the next sections, by specifying

the shape functions Ψ

(z) the weighted residual state-

ment (6) can be reduced to a system of ordinary dif-

ferential equations in α

(t), i.e., the semi-discrete ver-

sion of problem (1),

˙x(t) = M

u(t) − c D

x(t) + b

∗

(t) . (7)

In this system, M

is called the global mass matrix

and D

is the global diffusion matrix, and b

∗

repre-

sents the boundary conditions. The vector x(t) and

˙x(t) are the state vectors of the unknown weighting

coefﬁcients α

(z) and their derivatives

x(t) =



(t), α

(t), · · · , α

dof

−1

(t)



It is important to note that the entries of the matrices

and D

, and the state vector x(t) merely de-

pend upon the choice of the shape functions Ψ

(z), as

shown in the following sections.

The next sections are devoted to appropriate def-

initions of the shape functions Ψ

(z). First, the h-

type expansion functions decomposing the solution

domain into small subdomains are considered; Ψ

(z)

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

are usually linear functions or simple polynomials.

Then, based on this decomposition it is possible to in-

troduce additional supporting nodes within the subdo-

mains; the so-called nodal p-type expansion functions

using higher-order orthogonal polynomials. Finally,

the shape functions Ψ

(z) can be deﬁned by a set of

orthogonal polynomials of different order or modes,

called modal p-type expansion functions. For each

type it is shown that the global mass matrix M

and

the global diffusion matrix D

can be calculated in a

similar manner.

3.2 Elemental Decomposition

(h-type extension)

In this section, the decomposition of the solution do-

main Ω into small subdomains Ω

is demonstrated in

more detail, which is referred to as the h-type exten-

sion process. This process basically reduces the sizes

of the individual subdomains Ω

in order to achieve

convergence of the approximated solution.

Here, the decomposition process is explained and

visualized by means of simple polynomials for the

shape functions Ψ

(z). However, the same techniques

can be exploited with higher-order polynomial ex-

pressions, as shown in the next sections. The decom-

position of the solution domain into subdomains and

the respective shape functions for linear polynomials

are visualized in Fig. 2.

Substituting the ﬁnite expansion (4) into the weak

formulation (6) of the partial differential equation

yields the following individual terms of the weak for-

mulation

Ω

(z)

∂

f(z, t)

∂t

dz =

dof

−1

j=0

dα

(t)

Ω

dΨ

(z)

∂

f(z, t)

∂z

dz =

dof

−1

j=0

(t)

Ω

(z)˜s(z, t)dz =

dof

−1

j=0

ˆs

(t)

The individual entries M

and D

, deﬁned by

Ω

(z)Ψ

(z)dz ,

Ω

dΨ

(z)

dΨ

(z)

dz ,

can be assembled to the global mass matrix M

and

the global diffusion matrix D

, respectively. At this

point it can be easily recognized that this always leads

to the ordinary differential equation given in (7).

Furthermore, it is noted that in the case of linear

shape functions Ψ

(z) this leads to ﬁnite-difference

z = χ

(ξ)

(b)

(a)

(c)

(z)Ψ

(z)

−1

−11

(ξ)

f(z, t)

(t)

Nodal expansion modes (global bases)

Nodal expansion modes (local bases)

Figure 3: Approximation of the solution f(z, t) by means

of a nodal polynomial expansion, e.g. Legendre polynomi-

als for m = 4 reﬁnement. (a) Elemental decomposition

of the solution domain Ω into several subdomains Ω

. (b)

Shape functions Ψ

(z) for a nodal polynomial expansion

visualized in global bases, and (c) in local bases (standar d

element).

formula, which can be regarded as a special case of

the ﬁnite-element method (Baker, 1983).

3.3 Nodal Polynomial Expansion

This section describes how the weak formulation (6)

is decomposed in space using higher order polynomi-

als; also called p-type expansion. Assuming a ﬁxed

mesh, these methods achieve a higher accuracy of the

solution by increasing the polynomial order inside the

element.

Since a consideration of the expansion in terms of

global modes Ψ

(z) is uneconomical and numerically

intractable, especially when using a large number of

elements, it is reasonable to introduce a standard ele-

ment Ω

, such that

Ω

= {ξ | − 1 ≤ ξ ≤ 1} .

This standard element Ω

can be mapped to any el-

emental domain Ω

using the isoparametric transfor-

mation χ

(ξ), which expresses the global coordinate

z in terms of the local coordinate ξ, depicted in Fig. 3

(b)-(c).

A class of nodal p-type expansions which also have

become known as spectral elements are based on the

Legendre polynomials. Those polynomials are de-

BAYESIAN ESTIMATION OF DISTRIBUTED PHENOMENA USING DISCRETIZED REPRESENTATIONS OF

PARTIAL DIFFERENTIAL EQUATIONS

ﬁned in the standard domain Ω

according to

(ξ) =

(ξ

− 1)

dξ

where m denotes the degree of the used polynomial.

Based on the Legendre polynomials the spectral ele-

ments are given by

(ξ) =

(1 − ξ

(ξ)

m(m + 1)L

(ξ

)(ξ

− ξ)

where L

is the Legendre polynomial of degree m,

denotes the differentiation with respect to the ar-

gument, and ξ

is the p-th Gauss-Lobatto-Legendre

quadrature point deﬁned by the corresponding root of

(1 − ξ

) L

(ξ) = 0.

The choice of these quadrature point plays an im-

portant role in the stability of the approximation. The

spectral elements ψ

(ξ) are shown in the standard do-

main Ω

in Fig. (3) for m = 4, (Fournier et al., 2004).

Finally, considering the approximated solution in

terms of the spectral elements ψ

(ξ), we can express

the approximate solution

f(z, t) in terms of ψ

(ξ) ac-

cording to

f(z, t) =

dof

−1

j=0

(z) α

(t) =

e=1

p=0

(ξ) α

(t)

(8)

where ψ

(ξ) = ψ

([χ

]

−1

(z)) contains the transfor-

mation from local bases to global bases in terms of the

parametric mapping χ

(ξ). The coefﬁcients α

(t) in

this form have a physical interpretation in that they

represent the solution of the partial differential equa-

tion (1) at the nodal points x

. This fact is exploited

for the derivation of a simple measurement gain ma-

trix H

, i.e., it turns out that it is reasonable to put the

sensor nodes onto the polynomial nodes, see Sec. 4.2.

Upon substituting the nodal expansion (8) into the

weak formulation of the partial differential equation

(6) the entries of the local mass matrices M

and lo-

cal diffusion matrices D

can be derived as

−1

(ξ)ψ

(ξ)dξ ,

−1

dψ

(ξ)

dξ

dψ

(ξ)

dξ

dξ . (9)

Considering the boundary conditions at the elemental

nodes, e.g. z

and z

in Fig. 3, the local matrices M

and D

can be easily assembled to the global mass

matrix M

and global diffusion matrix D

. This is

an automatic procedure known as global assembly.

3.4 Modal Polynomial Expansions

For the construction of p-type expansions it is often

favorable to select a set of orthogonal functions (poly-

(t) ··· α

(t) α

(t) ··· α

(t)

(b)

(a)

(c)

Modal expansion modes (global bases)

(z)

(z)Ψ

(z)

f(z, t)

Modal expansion modes (lo cal bases)

−1

(ξ)

Figure 4: Approximation of the solution f(z, t) by means

of a modal polynomial expansion, e.g. Legendre polyno-

mials for m = 5 reﬁnement. (a) Elemental decomposition

of the solution domain Ω into several subdomains Ω

. (b)

Shape functions Ψ

(z) for a modal polynomial expansion

visualized in global bases, and (c) in local bases (standar d

element).

nomials), such as Legendre, Chebyshev or sine func-

tions. The most commonly used orthogonal polyno-

mials in computational ﬂuid dynamics, which offer

some advantages compare to the other polynomials,

are based upon the Legendre polynomials. This p-

type modal expansion modes in the standard element

Ω

are deﬁned as

(ξ) =







1−ξ

p = 0

(1 − ξ

p−1

(ξ) 0 < p < m

1−ξ

p = m

(10)

where the lowest expansion modes ψ

(ξ) and ψ

(ξ)

are the same as the linear ﬁnite element expansion.

These modes are denoted as boundary modes since

they are the only modes which are nonzero at the ends

of the interval. In Fig. 4 the p-type modal expansion

based upon the Legendre polynomials is depicted for

m = 5, (Karniadakis and Sherwin, 2005).

Thus, the approximate solution

f(z, t) in terms

of a modal polynomial expansion can be expressed

in the same manner as the nodal polynomial expan-

sion (8); the function ψ

(ξ) is just replaced by p-

type modal expansion modes (10) and the coefﬁcients

(t) denote the weighting coefﬁcients for the indi-

vidiual modes.

The local mass matrices M

and local diffusion

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

matrices D

can be derived similar to the nodal poly-

nomial expansion (9). Considering the boundary con-

ditions at the end of each element, e.g. z

in Fig. 4,

the local matrices M

and D

can be easily assem-

bled to the global mass matrix M

and global diffu-

sion matrix D

4 TEMPORAL DISCRETIZATION

OF ODE-SYSTEM

In the previous section we presented the spatial de-

composition which allows the conversion of the par-

tial differential equation into a set of ordinary differ-

ential equation. In this section, we are now ready to

speciﬁy the time evolution leading to the discrete-time

system equation (2) and the discrete-time measure-

ment equation (3).

4.1 System Equation

To circumvent the restriction on the time step, ∆t,

it is reasonable to integrate the set of ordinary dif-

ferential equations (7) by means of implicit methods,

such as the Crank-Nicolson discretization. This pro-

duces a linear system of equations for the state vector

k+1

containing the unknown weighting factors α

the k + 1 time step, which is unconditionally stable.

Adding noise terms and modelling error terms leads

to following system equation

k+1

= A

+ B

+ b

+ w

, (11)

where the matrices A

and B

are determined using

the global mass matrix M

and the global diffusion

matrix D

. The vector b

containing the boundary

conditions is determined using the matrices M

, D

and the boundary vector b

∗

4.2 Measurement Equation

This section is devoted to the derivation of the

discrete-time measurement equation. The sensor

nodes, which are densely deployed inside the distrib-

uted phenomenon, are exploited to observe that phe-

nomenon and to improve its estimated state. That

means, the measurement of the i-th sensor node at the

location z = p

and at time step k, i.e., t = t

, is

related to the state vector x

according to

ˆy

, t = t

) =

dof

−1

j=0

) α

(t = t

)

= Ψ

) x

Assuming a sensor network consisting of L sensor

nodes, the measurement gain matrix H

is set up by

the shape function Ψ

) of order N , according to

ˆy







) · · · Ψ

)

) · · · Ψ

)







| {z }

+ v

, (12)

where v

are the measurement uncertainties. The

number of rows L of the matrix H

depends on the

number of used sensors, i.e., number of measurement

points, and the number of columns N depends on the

desired number of modes.

However, in the case of nodal expansion and as-

suming that the sensors are located at the polynomial

nodes the weighting coefﬁcients can be measured di-

rectly, i.e., α

(t) = ˆy

. In other words, the diagonal

entries of the measurement gain matrix H

are either

1 or 0, depending on the location of the sensor nodes,

ˆy







1 · · · 0

0 · · · 1







| {z }

+ v

. (13)

5 CENTRALIZED ESTIMATION

APPROACH

In this section the prediction step and the ﬁlter step for

a centralized estimation approach are derived. Due to

the fact that both the system equation (11) and the

measurement equation (3) are linear, it is sufﬁcient

to use the linear Kalman ﬁlter to obtain the best pos-

sible estimate for the system state characterizing the

distributed phenomena.

5.1 Prediction Step

The purpose of the prediction step is to propagate the

current state estimate ˆx

through the system equation

(11) to the next time step. Thus, the mean of the pre-

dicted state vector ˆx

k+1

at time step k + 1 is given

ˆx

k+1

= A

ˆx

+ B

ˆu

Assuming that the input vector u

and the state vector

are uncorrelated the covariance matrix is obviously

given by

k+1

= A

+ B

+ C

where C

is the covariance matrix of the input noise,

and C

is the covariance matrix of subsumed endoge-

nous uncertainties, e.g. modeling errors.

BAYESIAN ESTIMATION OF DISTRIBUTED PHENOMENA USING DISCRETIZED REPRESENTATIONS OF

PARTIAL DIFFERENTIAL EQUATIONS

0 L

(b)

(a)

Sensors

time t

f(z, t)

(1)

(3)

(5)

(7)

(9)

Figure 5: (a) Estimated solution

f(z, t). (b) Elemental de-

composition into two elements Ω

and Ω

with a polyno-

mial expansion of order m = 5 and location of sensor

nodes.

5.2 Filter Step

For the purpose of reducing the estimation uncer-

tainty, measurements are used that are related to the

state via the measurement equation (3). Given the pre-

dicted state ˆx

with covariance C

and a vector ob-

servation ˆy

with covariance C

, the estimated state

vector ˆx

is derived by

ˆx

=ˆx

+ C



+ H



−1



ˆy

− H

ˆx



In the uncorrelated case the covariance matrix of the

estimate is given by

= C

− C



+ H



−1

6 SIMULATION RESULTS

In this section we demonstrate the performance of the

proposed estimation method by means of some simu-

lation results. The goal is the reconstruction of the

temperature distribution in a heat rod using both a

physical model and measurements obtained by a sen-

sor network. It is important to note that the novelty of

our approach is to consider the uncertainties arising

from noisy measurements and occuring in the physi-

cal model (state vector and input vector).

The evolution of the temperature is modelled by the

well-known one-dimensional heat equation (1) of a

bar with the length L = 1m. The noisy input func-

tion is given by s(z, t) = 30 sin(2 t) + 30 + ∆u

where ∆u

denotes the input uncertainties. Applying

Element nodes

Sensor: ON OFF

time t

−1

log(3σ )-Bounds

Figure 6: Logarithm of the 3σ-Bounds as a measure for

the uncertainty of the estimated solution

f(z, t). Due to

the measurements the uncertainty can be decreased rapidly,

even between the sensor nodes.

a nodal expansion (8) for the approximated solution

f(z, t) = Ψ

(z) α(t), the inﬁnite-dimensional par-

tial differential equation (1) can be spatially and tem-

porally decomposed leading to the ﬁnite-dimensional

state space form (11). The state vector x

can be de-

rived by temporal discretization of the weighting fac-

tors α(t) of the approximated solution, as shown in

Sec. 4. Here, we assume a nodal expansion based on

a Legendre polynomial of the order m = 5. The spa-

tial decomposition of the heat rod into two elements

Ω

and Ω

is visualized in Fig. 5 (b).

Furthermore, it is assumed that for simplicity the

sensor network consists of two sensor nodes located

at z

= 0.25 and z

= 0.75, shown in Fig. 5 (b). In

the case of a nodal expansion the general relation be-

tween the measurement vector ˆy

and the state vector

described by (12) can be simpliﬁed to (13). For

this simulation example that means the state variables

(3)

and x

(7)

can be measured directly, as it is visual-

ized in Fig. 5 (b).

The estimated solution

f(z, t) is visualized in Fig.

5 (a) and the logarithm of the 3σ-bound of the es-

timated solution

f(z, t), which is a measure for its

uncertainty, is depicted in Fig. 6. It is obvious that

the measurements are used for rapidly decreasing the

uncertainty. Due to the model-based approach they

can be decreased even between the sensor nodes; the

remaining uncertainty merely arises from the model

uncertainties.

The estimation results for both a measurement

point and a non-measurement point are visualized in

Fig. 7. Again, it can be easily seen that the solution

f(z, t) is estimated even at non-measurement points

with an appropriate certainty. Furthermore, it is clear

that by means of the measurements the estimated so-

lution

f(z, t) can be signiﬁcantly improved.

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

Sensor ON

24 810time t

f(z =0.25, t)

f(z =0.5, t)

(b)

(a)

Figure 7: Estimated solution

f(z, t) (blue), 3σ-Bounds

(green), and analytic solution f (z, t) (red) at (a) measure-

ment and (b) non-measurement point.

7 CONCLUSION

This paper introduced the methodology for deriv-

ing system models and measurement models for the

reconstruction of distributed phenomena character-

ized by means of linear partial differential equations.

Thanks to the inhomogeneous approximation capabil-

ities and the systematic manner of this approach, the

estimation of nonlinear phenomena even with com-

plex geometries is possible. The novelty of this paper

is the model-based reconstruction of distributed phe-

nomena under the consideration of uncertainties both

occuring in the physical model and arising from noisy

measurements.

It is believed that applying such methods in sensor

network applications for the reconstruction provides

novel prospects to optimal sensor node placement, op-

timal measurement time sequences, and improvement

of the used physical model. The performance of the

proposed model-based approach for the reconstruc-

tion of distributed pheonmena was demonstrated by

means of simulation results for the one-dimensional

partial differential equation.

Although for the one-dimensional partial differen-

tial equation, the decomposition may seem unneces-

sarily involved; however, the same principles can eas-

ily be applied to the decomposition in multiple dimen-

sions. This is left for future research work. Further-

more, especially for large sensor networks it is essen-

tial to ﬁnd a decentralized reconstruction approach. It

is believed that the decomposition method introduced

in this paper is well-suited for such an estimation ap-

proach.

ACKNOWLEDGEMENTS

This work was partially supported by the German

Research Foundation (DFG) within the Research

Training Group GRK 1194 “Self-organizing Sensor-

Actuator-Networks”.

REFERENCES

Anderson, B. D. O. and Moore, J. B. (1979). Optimal Fil-

tering. Prentice-Hall.

Baker, A. J. (1983). Finite Element Computational Fluid

Mechanics. Taylor and Francis.

Culler, D. E. and Mulder, H. (2004). Smart sensors to net-

work the world. In Scientiﬁc American.

Faulds, A. L. and King, B. B. (2000). Sensor location in

feedback control of partial differential equation sys-

tems. In CCA’00, Proceedings of the 2000 IEEE In-

ternational Conference on Control Applications.

Fournier, A., Bunge, H.-P., Hollerbach, R., and Vilotte, J.-P.

(2004). Application of the spectral-element method to

the axisymmetric navier-stokes equation. In Geophys-

ical Journal International.

Hanebeck, U. D., Briechle, K., and Rauh, A. (2003). Pro-

gressive bayes: A new framework for nonlinear state

estimation. In Proceedings of SPIE, AeroSense Sym-

posium.

Karniadakis, G. E. and Sherwin, S. (2005). Spectral/hp

Element Methods for Computational Fluid Dynamics.

Oxford University Press.

Kumar, T., Zhao, F., and Shepherd, D. (2002). Collabora-

tive signal and information processing in microsensor

networks. In IEEE Signal Processing Magazine.

Levin, J. G., Iskandarani, M., and Haidvogel, D. B. (2000).

A nonconforming spectral element ocean model. In

International Journal for Numerical Methods in Flu-

ids.

Ortmaier, T., Groeger, M., Boehm, D. H., Falk, V., and

Hirzinger, G. (2005). Motion estimation in beating

heart surgery. In IEEE Transactions on Biomedical

Engineering.

Rao, B., Durrant-Whyte, H., and Sheen, J . (1993). A fully

decentralized multisensor system for tracking and sur-

veillance. In International Journal of Robotics Re-

search.

Roberts, K. and Hanebeck, U. D. (2005). Prediction and re-

construction of distributed dynamic phenomena char-

acterized by linear partial differential equations. In

Fusion’05, The Eight International Conference on In-

formation Fusion.

Thuraisingham, B. (2004). Secure sensor information man-

agement and mining. In IEEE Signal Processing Mag-

azine.

BAYESIAN ESTIMATION OF DISTRIBUTED PHENOMENA USING DISCRETIZED REPRESENTATIONS OF

PARTIAL DIFFERENTIAL EQUATIONS