A NEW METHOD FOR REJECTION OF UNCERTAINTIES IN
THE TRACKING PROBLEM FOR ROBOT MANIPULATORS
Juan A. Méndez, S. Torres, L. Acosta, E. González
Dep. de Ing. de Sistemas y Automática y Arq. y Tec. de Computadores, Universidad de La Laguna, Tenerife, Spain
V. M. Becerra
The University of Reading. Dep.of Cybernetics, Whiteknights, Reading RG6 6AY. United Kingdom
Keywords: Adaptive control, robot manipulators, robust control, parametric uncertainty.
Abstract: This paper presents a new strategy for robust tracking in robot manipulators. The aim of the strategy is to
reject parametric uncertainties due to model or load disturbances. The basic controller acting on the
manipulator is a robust controller designed by Lyapunov’s direct method. Acting on this controller there is
an adaptive system responsible for the adaptation of the basic parameter of the robust feedforward term. The
performance of the strategy is tested in a Puma-560 manipulator. A comparison with existing techniques is
done to verify the efficiency of the presented controller.
1 INTRODUCTION
There are circumstances in which the performance
of conventional controller of robot manipulator
decreases. For instance when the dynamics of the
robot are not precisely known or disturbances are
affecting the system, the controller could perform
poorly. In many of the control schemes the dynamic
model is explicitly used to compute the control
action. These techniques are based on a perfect
knowledge of the robot model and its dynamic
parameters. A perfect cancellation of the nonlinear
dynamics is achieved if those two premises are
satisfied, and linear controllers can then be used with
satisfactory performance.
There are other techniques that do not use this
exact feedback linearization approach but a local
linearisation around the desired trajectory (Torres et
al, 2002) or the property of linear parameterizability
of n-link rigid robots to obtain a linear model of the
system (Spong, 1992).
In this paper the imperfect cancellation of the
nonlinear dynamics due to uncertainties is afforded.
Lot of works related with adaptive control schemes
(Ortega and Spong, 1989; Slotine and Li, 1987),
robust control schemes (Slotine, 1985; Spong and
Widyasagar, 1987; Dawson et al, 1992) and even
hybrid control schemes (Su and Stepanenko, 1997)
have been proposed to deal with these uncertainties.
Most of robust controllers are based on the
Lyapunov’s direct method (LDM). These schemes
add a robust term to the control input that tries to
compensate the discrepancies between the estimated
model and the real model of the system. This robust
action presents a good performance in several
circumstances, but it has to be revised at least in two
cases. First, when the robot works with different
payload masses, and second, when the controller is
used with a robot manipulator having different
dynamic parameters than the estimated model. Due
to this, the robust action has to vary adequately. The
present work tries to add an adaptive scheme in
order to tune automatically the robust design
parameter involved in this action.
2 CONTROLLER DESIGN
The control problem considered is the tracking
problem of robot manipulators with uncertainties in
the model. The controller has three parts (Spong,
1992; Sciavicco and Siciliano, 1996): a feedback
linearisation inner loop, a stabilizing PD control law
and a robust action.
474
A. Méndez J., Torres S., Acosta L., González E. and M. Becerra V. (2006).
A NEW METHOD FOR REJECTION OF UNCERTAINTIES IN THE TRACKING PROBLEM FOR ROBOT MANIPULATORS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 474-477
DOI: 10.5220/0001204404740477
Copyright
c
 SciTePress

The dynamics of this system are represented by:
()( ) () ()
(
)
()() tctthttDtu θθθθθ ++=

,)()( (1)
being
()() tD θ the inertia matrix, ()
(
)
()
tth θθ

,
the
Coriolis and centrifugal force vector,
(
)
(
) tc
θ
the
gravitational force vector and u(t) the applied torque
to each link
The linearization is achieved considering the
following input to the nonlinear model:
()
(
)
()
kkkkkk
chyD θθθθτ ++=

, (2)
where y
k
is the new input to the linear resultant
model. The sub-index k indicates the instant of time,
while
θ
k
and
k
θ

refers to the measured position and
velocity at the instant k. This leads to the following
linear and decoupled second-order model:
kk
y θ

=
(3)
The following equation ensures an asymptotically
stable second-order system (the time dependence is
avoided in the notation for simplicity):
kkDkpk
rKKy +−−= θθ

(4)
where the components r
ik
of the vector r
k
are the
reference for each joint. This can be seen taking into
account equations (3) and (4), which leads to the
second-order system:
kpkDkk
KKr θθθ ++=

(5)
which is asymptotically stable if K
p
and K
D
are
positive definite matrices. Moreover, choosing a
diagonal form for them, the system results
decoupled. Once any desired trajectory
θ
d
(t) is
given, the tracking problem for this trajectory is
solved by choosing:
dkpdkDdkk
KKr
,,,
θθθ ++=

(6)
This is easy to view substituting (6) into (5), which
leads to:
0
~
~
~
,,,
=++
dkpdkDdk
KK θθθ

(7)
where
kdkk
θθθ −=
,
~
(and similarly for its time
derivatives). This equation gives the expression for
the dynamics of the position errors. Finally,
following (4) and (6), the stabilizing control law is
defined by:
kpkDdkk
KKy θθθ
~
~
,
++=


(8)
The third part of the controller is the robust action
added to correct the imperfect compensation of the
nonlinear term in (1), given by the inverse dynamics
control (2). In the assumption that only an estimation
of the real matrices D(
θ ), h( θ , θ

) and c( θ ) can be
obtained, the equation (7) results:
ηθθθ =++
dpddd
KK
~
~
~

(9)
where
η
gives the discrepancies between the real
and the estimated values for the matrices (Sciavicco
and Siciliano, 1996). In view of this, for this
nonlinear coupled system, tracking with zero error is
not ensured and PD control action is not sufficient.
Following the well-known LDM, an outer feedback
loop on the error can be designed in order to be
robust to the uncertainty
η :
k
t
k
t
rk
QD
QD
y ξ
ξ
ρ
=
,
(10)
where
Q
2n x 2n
is a positive definite matrix and ρ is a design
parameter. The full control law is given then by:
rkdkpdkDdkk
yKKy
,,,,
~
~
+++= θθθ


(11)
To avoid the problems in (10) when the error
approximates zero, the following expression is used:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<
≥
=
εξξ
ε
ρ
εξξ
ξ
ρ
k
t
k
t
k
t
k
t
k
t
rk
QDifQD
QDifQD
QD
y
,
,
,
(12)
3 IMPROVING PERFORMANCE
OF EXISTING TECHNIQUES
The value of the design parameter ρ is important in
order to have a good performance of the closed-loop
,
0
2
⎥
⎦
⎤
⎢
⎣
⎡
=
nxn
nxn
nxn
I
D
.
~
~
1
1
12
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
xn
xn
xn
θ
θ
ξ

A NEW METHOD FOR REJECTION OF UNCERTAINTIES IN THE TRACKING PROBLEM FOR ROBOT
MANIPULATORS
475

system. Several proposals have exist in the literature
(Spong, 1992; Corless and Leitmann, 1981; Liu and
Goldenberg 1993; Jaritz and Spong, 1996).
In this paper a new method to adjust this critical
parameter is presented. An adaptive law based on a
gradient descent method is used for the adaptation of
the design parameter
ρ :
1
1
−
−
∂
∂
−=
k
k
kk
J
ρ
γρρ
(14)
where
γ is the learning rate of the adaptation. In this
case, the cost function is formed by two terms. The
first of them loads the error in the state of the robot.
The second term loads the resultant input to the load
system. The resultant cost function is given by:
111
2
1
2
1
)(
−−−
+=
kad
T
kkad
T
kkk
yRyQJ ξξρ
(15)
where the 2n x 2n matrix Q
ad
weighs the state error
and the n x n matrix R
ad
weighs the influence of the
inputs to the linearised system. This choice gives the
following adaptation law:
⎥
⎦
⎤
⎢
⎣
⎡
∂
∂
+
∂
∂
−=
−
−
−
−
−
1
1
1
1
1
k
k
ad
T
k
k
k
ad
T
kkk
y
RyQ
ρρ
ξ
ξγρρ
(16)
To compute the derivatives in (16), a first order
approximation has been applied. The error
ξ
k
can be
approximated by:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
−
h
kk
k
kd
kd
k
k
k
1
,
,
~
~
θθ
θ
θ
θ
θ
θ
ξ


(17)
Its derivate with respect to
ρ
k-1
is:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
−=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
−
∂
∂
∂
∂
−=
∂
∂
−
−
−
−
−
−
−
1
1
1
1
1
1
1
111
k
k
k
k
k
k
k
k
k
k
k
k
hhh ρ
θ
ρ
θ
ρ
θ
ρ
θ
ρ
θ
ρ
ξ
(18)
In order to compute this derivative, the linearised
model of the system in state-space form is used:
kk
kDkDk
Cx
yBxAx
=
+=
−−
θ
11
(19)
Then, the derivative of (18) is:
1
1
1 −
−
−
∂
∂
=
∂
∂
k
k
D
k
k
y
CB
ρρ
θ
(20)
If it assumed that
εεξ ∀< ,
k
t
QD , which is true
except perhaps at the beginning of the motion,
expression (11) can be approximated by:
kkdkpdkDdkk
MKKy ξρθθθ +++=
,,,
~~


(21)
where
ε /QDM
T
=
. Expression (21) leads to the
computation of the derivative in the right part of (20)
as follows:
1
1
1
−
−
−
=
∂
∂
k
k
k
M
y
ξ
ρ
(22)
Using (22) and (20), expression (18) is written as:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−=
∂
∂
−
−
−
1
1
1
1
kD
kD
k
k
MCB
h
MCB
ξ
ξ
ρ
ξ
(23)
Finally, expressions (22) and (23) can be used to
evaluate the adaptation law (16).
4 RESULTS
The algorithm proposed was tested on a PUMA 560
manipulator of Unimation. The model used includes
uncertainties with respect to the real model. In
Figure 1, the results of a trajectory-following
experiment is shown. As can be observed, the
performance of the RAC strategy is considerably
better than the other two. Robust controller with the
Spong strategy tends to reduce the tracking error, but
the new proposed strategy improves the performance
of the Spong controller. In both cases the uncertainty
bound parameter is bounded along the whole
trajectory. However, higher values are achieved with
the RAC scheme. Actually, this is the reason why
the performance is better with the proposed
controller.
ICINCO 2006 - ROBOTICS AND AUTOMATION
476

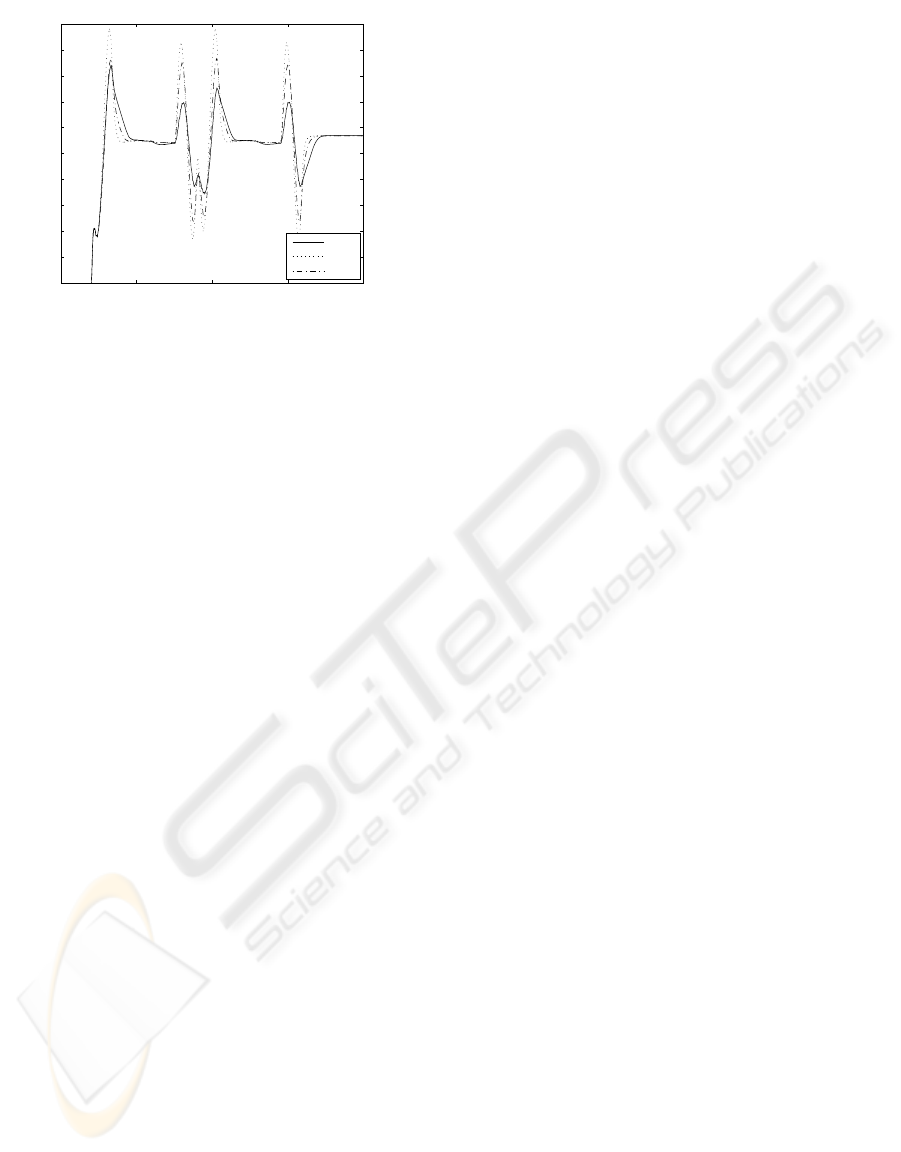
Figure 1: Tracking error comparison of the different
strategies for a tracking experiment (link 2).
It is important to take into account that to setup
the Spong’s controller it is necessary to previously
simulate the system in order to tune the parameters
0
υ
and
1
υ
in equation 13. However, with the RAC
scheme better results are obtained and it is not
necessary any previous simulation to setup the
controller.
5 CONCLUSIONS
In this work an efficient self-adaptive robust
controller applied in a PUMA 560 manipulator arm
was presented. It is studied the case in which model
uncertainties are present. The standard robust control
strategy for robot manipulators is based on a robust
controller with fixed design parameter or an
adaptation based on the behaviour of the model in
the defined reference trajectory. These schemes are
inefficient: first of them requires quite trial and error
proofs before reaching the appropriate value for the
design parameters, and it is valid only for the current
trajectory. Second of them requires an evaluation of
the dynamics terms over the reference trajectory in
order to get some bounds parameters to form the
adaptation law. The new self-adaptive strategy
designed improves the performance of the standard
controllers. It was shown that the robust design
parameter is very important in the closed-loop
behaviour of the controller. The new strategy adds a
self-tuning scheme in order to vary adequately its
value. The results obtained with this new scheme
show a better behavior than the standard scheme
REFERENCES
M. Corless and G. Leitmann (1981). “Continuous-state
feedback guaranteeing uniform ultimate boundedness
for uncertain dynamic systems”, IEEE Trans. On
Automatic Control, vol. AC-26, pp. 1139-1141.
D. Dawson and F. Lewis (1989). “Robust and adaptive
control of robot manipulator without acceleration
measurement”, in Proc. of IEEE Decision & Control,
Tampa, Florida.
D.M. Dawson, Z. Qu and J.J. Carroll (1992). “Tracking
control of rigid-link electrically-driven robot
manipulators”. Int. J. of Control, vol. 56. pp. 991-
1006.
A. Jaritz and M.W. Spong (1996). “An experimental
comparison of robust control algorithms on a direct
drive manipulator”, IEEE Trans. on Control Systems
Technology, vol. 4, no.6, pp. 627-640.
F. Lewis, D. Dawson and C. Abdallah (2004), Robot
manipulator control. New York: Marcel Dekker.
G. Liu and A. Goldenberg (1993), “On robust saturation
control of robot manipulators”, in Proc. 32nd Conf. on
Decision and Control, Texas, Dec. pp. 2115-2120.
L. Sciavicco and B. Siciliano (1996). Modelling and
Control of Robot Manipulators. London: Springer-
Verlag.
J.J.E. Slotine (1985). “Robust control of robot
manipulators”. Int J. of Robotics Research, vol. 4, pp.
49-64.
M.W. Spong and M. Widyasagar (1987). “Robust linear
compensator for nonlinear robotic control”. IEEE
Journal of Robotics and Automation, vol. RA-3. pp.
345-351.
M.W. Spong (1992). “On the robust control of robot
manipulators”, IEEE Trans. On Automatic Control,
vol. 37. pp. 1782-1786.
C.Y. Su and Y. Stepanenko (1997). “Redesign of hybrid
adaptive/robust motion control of rigid-link
electrically-driven robot manipulators”. IEEE Trans.
on Rob&Aut, vol. 14, pp. 651-655.
S. Torres, J.A. Méndez, L. Acosta, M. Sigut, G.N.
Marichal and L. Moreno (2001). “A predictive control
algorithm with interpolation for a robot manipulator
with constraints”. In Proc of IEEE Conf. on Control
and Applications, Mexico.
S. Torres, J.A. Méndez, L. Acosta, M. Sigut and G.N.
Marichal (2002). “Disturbances rejection on a robot
arm using an efficient predictive controller”. In Proc.
of the 15th IFAC World Congress, Barcelona, Spain.
0 5 10 15 20
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
time (sec.)
Position error link 2 (rad.)
RAC
PD
Spong
A NEW METHOD FOR REJECTION OF UNCERTAINTIES IN THE TRACKING PROBLEM FOR ROBOT
MANIPULATORS
477