MATRIX-BASED HIERARCHICAL FUZZY SYSTEMS

Santiago Aja-Fern

andez and Carlos Alberola-L

opez

∗

Laboratorio de Procesado de Imagen

ETSI Telecomunicaci

on, Universidad de Valladolid

Campus Miguel Delibes 47011 Valladolid, Spain)

Keywords:

Hierarchical fuzzy systems, FITM, transition matrices, SAM.

Abstract:

A matrix inference method for fuzzy systems is used to deal with hierarchical fuzzy systems (HFSs). A method

to decompose a multiple input fuzzy system into a HFS is presented. This method is based in representing

the structure of a fuzzy system using matrices. An example of such a conversion for a three-input system is

included.

1 INTRODUCTION

In fuzzy systems (FSs) and fuzzy controllers with

multiple inputs a rule-explosion problem arises when

the number of inputs is large. As the number of

rules increases, the rule base is less and less under-

standable to human users. This problem is known as

the curse of dimensionality, which in fuzzy systems

causes some well known problems related with com-

putational and memory usage, real-time performance,

and difﬁculty to properly deﬁne the system. One of

the methods proposed to overcome this problem is the

use of hierarchical fuzzy systems (HFSs); a complex

system with many rules is decomposed into a num-

ber of hierarchically-connected low-dimensional FSs.

These new systems, which turn out to be simpler than

the original, have usually smaller rule bases.

In this paper we will present a new method to carry

out this system decomposition. The method is based

on a matrix procedure known as FITM (Fast Infer-

ence using Transition Matrices) (Aja-Fern

andez and

Alberola-L

opez, 2004a), which has been proposed

as a methodology to perform inferences in SAM

(Standard Additive Model (Kosko, 1997)) FSs efﬁ-

ciently. It is based on representing each input to the

FS as a vector and the overall fuzzy inference pro-

cedure becomres a simple matrix operative. FITM

is a procedure initially intended for Computing with

∗

The authors acknowledge the CICyT for research grant

TEC2004-06647-C03-01, the FIS for grant PIO-41483, the

Junta de Castilla y Le

on for grant VA075A05 and the Euro-

pean Commission for the funds associated to the Network

of Excellence SIMILAR (FP6-507609).

Words (Zadeh, 1996) environments, but it may ﬁnd

applicability in other ﬁelds, such as control and feed-

back systems.

1.1 Hierarchical Fuzzy Systems

It is easy to see that if a system has n input vari-

ables and each variable has m terms (deﬁned over

m fuzzy sets) the system has a complete set of m

different rules (Raju et al., 1991). Moreover, as pre-

viously stated, the rule base is less and less under-

standable to human users as the number of rules in-

creases. Originally HFSs were proposed to overcome

this problem. Instead of having one complex system

with many rules, the system was decomposed into a

number of hierarchically-connected low-dimensional

FSs. These new systems, which turn out to be simpler

than the original, have smaller rule bases, a fact that

makes them more transparent to the designer. If the

number of intermediate variables is small enough

the HFS has also fewer rules than the original system.

One of the ﬁrst approaches is due to Raju, Zhou

and Kisner (Raju et al., 1991; Raju and Zhou, 1993).

An adaptive HFS is introduced in order to facilitate

the tuning of the parameters of a controller. Their aim

was to design a series of hierarchical fuzzy processors

with a small number of input variables distributed in

each processor. Yager in (Yager, 1993) suggested an

extension of the basic FS modeling framework. The

purpose of this extension was to allow for a prioriti-

A simple criterion to quantify this “enough” can be

found in (Lee et al., 2003).

Aja-Fernández S. and Alberola-López C. (2006).

MATRIX-BASED HIERARCHICAL FUZZY SYSTEMS.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 92-97

DOI: 10.5220/0001206500920097

 SciTePress

zation of the rules by using hierarchical representa-

tion of the rules. This new representation is known as

Hierarchical Prioritized Structure (HPS). In (Hor

cek

and Binder, 1997) Hor

cek and Binder discussed two

structures of hierarchically-organized groups of rules:

series and parallel hierarchies . The aim of this work

is to design a nonlinear controller whose rules were

transparent to the designer. Many other approaches to

overcome the dimensionality problem based on HFS

have been proposed elsewhere (Holve, 2003; Lee

et al., 2003). Additionally, some authors have focused

on theoretical justiﬁcations of the approximation ca-

pability of HFS (Wang, 1998; Zeng and Keane, 2005).

In the HFS literature a fuzzy set with two inputs and

one output is known as Fuzzy Logic Unit (FLU). De-

pending of the connection between the FLUs in a hi-

erarchical decomposition of a MISO-FS, we can have

three main types of hierarchical models (Hor

cek and

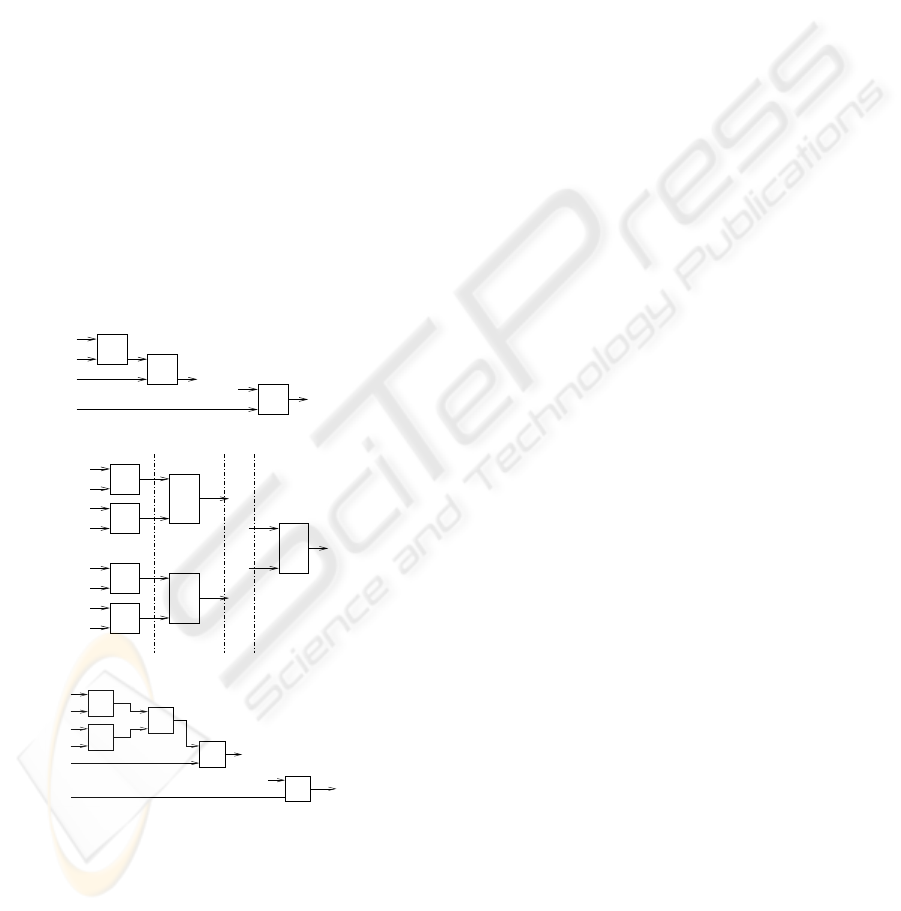
Binder, 1997; Kikuchi et al., 1998) as shown in Fig. 1

(although one may think of more): Serial HFS, where

the inputs to the FLUs are the outputs of the previous

FLUs and an external input; Parallel HFS, where the

inputs to the FLUs are the outputs of two FLUs of the

previous layer and Hybrid HFS.

. . .

= y

N−1

N+1

Serial HFS

. . .

Layer 2 Layer iLayer 1

2N−1

2N−2

2N−3

Parallel HFS

. . .

Hybrid HFS

Figure 1: Different hierarchical models.

In the following sections we will show how to deal

with HFSs using transition matrices. This method

was previously introduced in (Aja-Fern

andez and

Alberola-L

opez, 2004b).

2 BACKGROUND ON FITM

The FITM procedure was originally proposed in (Aja-

Fern

andez and Alberola-L

opez, 2004a) to perform in-

ferences efﬁciently in the SAM-FSs (Kosko, 1997);

its result is proportional to the inference output given

by a SAM-FS, and it is totally equivalent to the SAM-

FS in terms of the output centroid. The beneﬁt of

FITM is the considerable reduction of the overall

computational complexity in the inference process,

provided that an initial assumption is held; speciﬁ-

cally, inputs are required to be linear combinations of

the fuzzy sets that the input linguistic variable (LV)

consists of. If this is so, each input is represented as

a vector in the input space, with components equal to

the contribution of each fuzzy set of the input linguis-

tic variable to the current input.

This requirement holds in computing with words

(CWW) (Zadeh, 1996) applications, where the in-

puts to the FS are words, concepts or labels, mod-

eled as fuzzy sets. Additionally, this sort of inputs

can also be found in those problems where the out-

put of one SAM-FS is the input of another one. This

is clearly the case of hierarchical systems. General

inputs and particularly, crisp inputs, can indeed be

dealt with; in this case there would be no computa-

tional savings with FITM, but some beneﬁts can be

obtained from the matrix representation of the sys-

tem. An extension of the procedure to non-linear op-

erators (i.e. generic t-norms and t-conorms) has also

been reported in (Aja-Fern

andez and Alberola-L

opez,

2005). Following, we describe the method to build a

FITM inference engine when linear operators (SAM)

are used and (crisp) numerical inputs are considered;

attention will be focused on the 2-input single out-

put case (2-ISO). Only conclusions will be described

here. Details can be found in (Aja-Fern

andez and

Alberola-L

opez, 2004a).

Assume a 2-input single output FS, with inputs X

and Y and output Z. The inputs and the output are

all (crisp) numbers. For each input and the output a

linguistic variable (LV) is deﬁned. Assume that the

ﬁrst input LV consists of M possible fuzzy sets A

deﬁned on the universe U ⊂ R; the second input Y is

a LV consisting of N possible fuzzy sets B

deﬁned

on the universe V ⊂ R and the output LV consists

of L possible fuzzy sets D

deﬁned on the universe

W ⊂ R.

The whole SAM inference process may be ex-

pressed using transition matrices as

γ =

l=1

Ω

β (1)

with Ω

an array of transition matrices of the system.

γ is the output vector and α and β are the input vec-

MATRIX-BASED HIERARCHICAL FUZZY SYSTEMS

tors deﬁned as

β =







)



















(2)

being x

the numerical input. α is deﬁned in a sim-

ilar way using sets B

and the numerical input y

In order to build the transition matrices we must de-

ﬁne some intermediate data structures that can be dis-

carded once matrices Ω

have been calculated. How

to build these matrices is now addressed.

First step is to create the activation matrix of each

input. As both inputs will be crisp, they will make

use of identity matrices, i.e. R

and R

, will be the

M × M and the N × N matrices respectively. Next

step is to calculate the set of matrices G

, 1 ≤ l ≤ N ,

that bear the relation between inputs

= R

⊗ [R

] (3)

where ⊗ is the Kronecker tensor product (Golub and

Loan, 1996). E

is a column selection vector, i.e., a

column vector with all entries zero but the one at row

l, 1 ≤ l ≤ N, the value of which is unity. This vector

has the purpose of extracting column l from matrix

The rule base of the system is coded in matrix C.

This is a selection matrix with as many rows as rules

in the rule base and, for row j, all the entries are zero

but the one at column i if the output consequent for

rule j is D

C =

· · · D

M×N

0 0 · · · 1

0 1 · · · 0

. . . . . . . . .

1 0 · · · 0

(4)

As for matrix C, rules in the rule base are ordered

by varying the second antecedent for each value of

the ﬁrst antecedent (see Appendix I in (Aja-Fern

andez

and Alberola-L

opez, 2004a)).

Finally, the transition matrices are calculated by

Ω

= C

l = 1, · · · N (5)

The output centroid, if desired, can be calculated from

the output vector γ by

out

· · · c

]γ

[1 1 · · · 1]γ

(6)

with c the vector of the output set centroids c

(1 ≤

i ≤ L) and γ as deﬁned in equation (1). one from the

conventional SAM-FS.

For the case of a multiple-input single-output

(MISO) FS the expressions are extended accordingly.

The relation among coefﬁcients is now given by:

γ =

· · ·

· · · α

Ω

j=1

β (7)

where α

and β are the input vectors and Ω

j=1

are the transition matrices of the system.

3 HIERARCHICAL

DECOMPOSITION OF FS

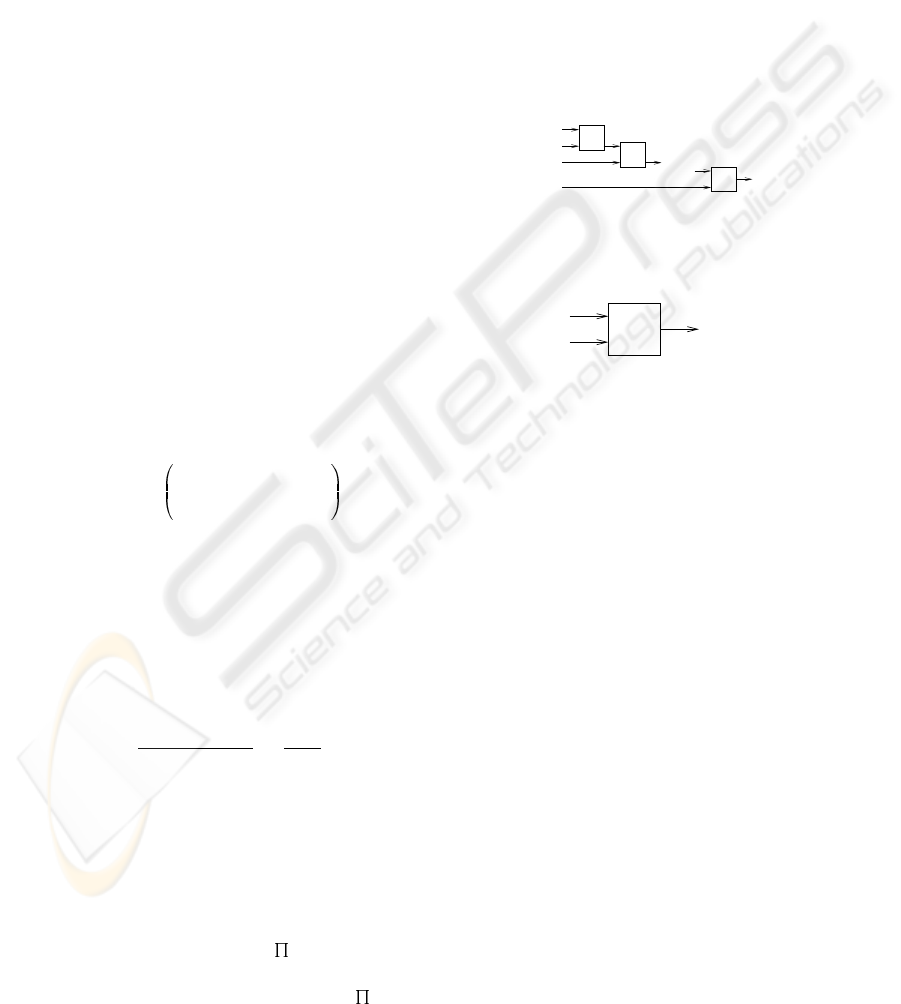
Consider the serial HFS shown in Fig. 1. A re-

interpretation of this system using transition matrices

and vectors is shown in ﬁg. 2. The different inputs

and outputs to the system can be viewed as vectors

in their respective spaces. As it has been indicated in

section 2, these vectors represent a linear combination

of the sets of each linguistic variable, or, in the case

of crisp inputs, the activation of each set by this input.

Input variables x

will be represented by vectors α

and output variables y

by vectors γ

. Each FLU can

be characterized by an array of matrices Ω

. . .

N+1

N−1

Ω

Figure 2: A HFS in FITM notation.

Ω

i+1

i−1

Figure 3: Single FITM block. For i = 1 γ

i−1

= α

A single block of the whole system (a FLU rewrit-

ten in FITM terminology) is showed in 3. For the

(i ≥ 2) block the inputs will be the vectors γ

i−1

and α

i+1

, and the output the vector γ

. According to

eq. (1) the inference process is performed following

the equation

i+1

Ω

i−1

(8)

Vector γ

i−1

is the output of the previous block and

i+1

is an external input. According to eq. (8) we

can write the output of the overall system as

γ =

N+1

Ω

· · ·

Ω

(9)

which can be rewritten as

γ =

· · ·

N+1

· · · α

Ω

· · · Ω

· · ·

N+1

· · · α

Ω

···l

(10)

This is the FITM inference equation for a MISO sys-

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

. . .

N+1

Ω

Figure 4: Multiple Input Single Output fuzzy system.

tem as the one shown in ﬁg. 4, with its transition ma-

trices deﬁned as

Ω

···l

= Ω

· · · Ω

Ω

(11)

There is an equivalent relation between the transition

matrices of a MISO FS and the matrices of each FLU

of the derived HFS. Knowing the matrices of the FLU

of the HFS we can easily calculate the matrix of the

overall system. The inverse procedure is also possi-

ble.

3.1 From MISO to HFS. Special

Case: 3ISO

Consider a fuzzy system with 3 inputs and 1 output,

as shown in ﬁg. 4. The imputs will be x

(M possi-

ble fuzzy sets, vector α

), x

(N possible fuzzy sets,

vector α

) and (x

: P possible fuzzy sets, vector α

The output is y (Q possible fuzzy sets, vector γ). The

inference can be carried out using an array of transi-

tion matrices Ω

, with i = 1, . . . , N , j = 1, . . . , P

and size Q × M. An equivalent HFS to this system

will be the one shown in ﬁg. 5. Two FLUs replace

the 3-ISO FS. The output of the ﬁrst block is modeled

by a vector β, deﬁned over a space with K possible

fuzzy sets. The value of K will be discussed later.

Both systems are deﬁned by its transition matrices,

Ω

(Q × K size, i = 1, · · · , P ), and Ω

(K × M

size, j = 1, · · · , N ).

Ω

Figure 5: Equivalent HFS.

There is a relation between the matrices of the 3-

ISO and the hierarchical systems:

Ω

= Ω

(12)

This relation can be rewritten using block matrices as

Ω

(

Ω

· · · Ω

) =



Ω

· · · Ω

. . . . . .

Ω

· · · Ω



Ω

[QP ×K]

Ω

[K×M N ]

= Ω

[QP ×MN ]

(13)

The solutions of this system are determined by the

rank of matrix Ω

. It will also determine the number

of sets in the transition space, as the minimum num-

ber of columns of matrix Ω

is the rank of matrix Ω

Speciﬁcally K ≥ rank(Ω

). We choose the equality

to obtain the minimum-size matrices. If a decompo-

sition of matrix Ω

according to eq. (13) is feasible,

the hierarchical system determined by matrices Ω

and Ω

will be totally equivalent to the original sys-

tem.

3.2 Optimizing the HFS

The decomposition process described in section 3.1

assumes that the inputs are arranged in a particular

order, but this order is somehow arbitrary. A different

arrangement will give rise to a different matrix Ω

and therefore to a different decomposition in FLUs.

For a 3ISO system, as the one in the previous sec-

tion, there are three possible arrangements; each of

them gives rise to a different system (see ﬁg. 5):

• [x

, x

]: x

will be the external input to the sec-

ond FLU (this is the one indicated in Fig. 5).

• [x

, x

]: x

will be the external input to the sec-

ond FLU.

• [x

, x

]: x

will be the external input to the sec-

ond FLU.

We can also think in other possibilities, such as

, x

], but the ﬁnal HFS will be the same one

as in the ﬁrst case. Assuming that the rearranged in-

puts are [x

, x

], with size N

, N

and N

the

total number of rules in the 3ISO system and in the

HFS will be N

3ISO

= N

× N

and N

HF S

×N

+K × N

, being K = rank(Ω

). In order to

have the minimum number of rules, we must choose

the arrangement of the inputs that minimize N

HF S

3.3 An Example

Suppose a fuzzy system with 3 inputs x, θ and

θ and

one output y. Each input and the output are deﬁned as

a linguistic variable with 3 possible fuzzy sets: Posi-

tive (P), Zero (Z) and Negative (N). The rule base for

this system is on table 1.

The inference can be carried out using FITM. The

system will be a 3ISO system as the one in ﬁg. 4. The

output will be the centroid of

γ =





Ω





being γ the output vector, and α

the input vectors.

Accepting that the inputs are crisp values, these vec-

tors are deﬁned as

= [P (x

) Z(x

) N (x

)]

MATRIX-BASED HIERARCHICAL FUZZY SYSTEMS

1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 1 1 0 1 0 0 0 0 0

0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0

0 1 1 1 0 0 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 0 0 0 0 1 1

(14)

Table 1: Rule base for the example.

x θ

θ y

P P P P

P P Z N

P P N N

P Z P N

P Z Z P

P Z N Z

P N P Z

P N Z N

P N N N

Z P P Z

Z P Z N

Z P N N

Z Z P N

Z Z Z P

Z Z N P

Z N P P

Z N Z P

Z N N N

N P P P

N P Z P

N P N N

N Z P P

N Z Z Z

N Z N Z

N N P Z

N N Z N

N N N N

As indicated before, the activation matrices R

, R

and R

are the 3 × 3 identity matrix. The selection

matrix C is on eq. (14). The resulting transition ma-

trices are (if an ordering [x, θ,

θ] is assumed)

Ω

1 0 1

0 1 0

0 0 0

Ω

= Ω

0 0 1

0 0 0

1 1 0

Ω

= Ω

0 1 0

1 0 1

0 0 0

Ω

1 1 0

0 0 1

0 0 0

Ω

= Ω

0 0 0

1 1 1

Once the whole system is deﬁned we can make the

HFS decomposition. To build the Ω

matrix in

eq. (13) we have three different ways of ordering the

inputs:[x, θ,

θ], [x,

θ, θ] and [θ,

θ, x]. So, three differ-

ent Ω

matrices can be built:

Ω

1 0 1 0 0 1 0 1 0

0 1 0 0 0 0 1 0 1

0 0 0 1 1 0 0 0 0

0 0 1 1 1 0 0 0 0

0 0 0 0 0 1 0 0 0

1 1 0 0 0 0 1 1 1

0 0 0 0 1 0 0 0 0

0 0 0 1 0 1 0 0 0

1 1 1 0 0 0 1 1 1

Ω

1 0 1 0 0 1 0 0 0

0 1 0 0 0 0 0 0 0

0 0 0 1 1 0 1 1 1

0 0 1 1 1 0 0 1 0

0 0 0 0 0 1 1 0 1

1 1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 0 0

1 0 1 0 0 0 0 0 0

0 0 0 1 1 1 1 1 1

Ω

1 0 0 0 1 0 0 0 0

0 0 1 0 0 0 0 1 0

0 1 0 1 0 1 1 0 1

0 0 1 0 1 0 0 1 0

1 0 0 0 0 0 0 0 0

0 1 0 1 0 1 1 0 1

1 1 0 1 0 0 0 0 0

0 0 1 0 1 0 0 1 0

0 0 0 0 0 1 1 0 1

the ranks of which are rank(Ω

) = 6, rank(Ω

) =

6 and rank(Ω

) = 5. The number of rules in the

original system is 3 × 3 × 3 = 27. In the HFS we

have 3 × 3 + rank(Ω

) × 3 rules. So we choose the

third matrix (the one with smaller rank) to build the

HFS.

According to eq. (13) we may ﬁnd two matrices

Ω

and Ω

so that Ω

Ω

= Ω

. One way to do

it is using a LU factorization, and use some further

algebra to eliminate redundant lines. By doing so, we

obtain matrices Ω

and Ω

and the transition matri-

ces for each FLU will be

Ω

1 0 0 0 0

0 0 1 0 0

0 1 0 0 0

Ω

0 0 1 1 0

1 0 0 −1 0

0 1 0 0 0

Ω

1 1 0 −1 −1

0 0 1 1 0

0 0 0 0 1

Ω







1 0 0

0 1 0

0 0 1

0 0 0







Ω







0 1 0

1 0 1

0 0 0

0 1 0

0 0 1







Ω







0 0 0

1 0 1

0 1 0

0 0 0

1 0 1







The inference using FITM can be done as

γ =

Ω

β =





Ω





ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

The system represented as a HFS is totally equivalent

to the one we departed from.

3.4 General Case

When the number of inputs is greater than 3, the HFS

can be obtained in a very similar way to the 3-ISO

system. Suppose a generic MISO system with N in-

puts x

, · · · , x

. The system can be represented us-

ing transition matrices

Ω

···l

= 1, · · · , M

· · · l

= 1, · · · , M

being M

the dimension of the i-th input. This system

is equivalent to a system with N inputs and another

system with two inputs, as shown in ﬁg. 6.

. . .

N−1

Figure 6: First step in hierarchical decomposition of a

MISO-FS.

To obtain the transition matrices of each system,

the following equation must be solved

Ω

···l

Ω

= Ω

···l

(15)

Written in matrix form

Ω

= Ω







Ω

11···1

Ω

21···1

Ω

···M









Ω

· · · Ω









Ω

11···1

· · · Ω

1···1

Ω

12···1

· · · Ω

2···1

Ω

···M

· · · Ω

···M







(16)

Matrices Ω

can be easily obtained from this equa-

tion. The same procedure is applied on the remaining

MISO system, until only two inputs are left.

As in the 3ISO case, the proper election of the or-

dering of the inputs will give a better size of the rule

base of each FLU. This size is related again with the

rank of matrix Ω

. When this optimization process

is carried out, the ﬁnal HFS system can be any of the

types introduced in section 1.1: serial, parallel or hy-

brid.

4 CONCLUSIONS

In this paper we have shown a simple procedure to

convert a large MISO FS into a serial HFS. Such a

conversion leads to a number of smaller rule bases

than the original, which, in turn, may facilitate human

interpretation and/or ﬁne tune the rule bases out of

examples.

REFERENCES

Aja-Fern

andez, S. and Alberola-L

opez, C. (2004a). Fast

inference in SAM fuzzy systems using transition ma-

trices. IEEE Trans. Fuzzy Systems, 12(2):170–182.

Aja-Fern

andez, S. and Alberola-L

opez, C. (2004b). Fuzzy

hierarchical systems wih FITM. In Proc. of FUZZ-

IEEE’04, Budapest, Hungary.

Aja-Fern

andez, S. and Alberola-L

opez, C. (2005). Fast

inference using transition matrices: An extension to

non-linear operators. IEEE Trans. Fuzzy Systems,

13(4):478–490.

Golub, G. and Loan, C. V. (1996). Matrix Computations.

The Johns Hopkins University Press, Baltimore, ME.

Holve, R. (2003). Rule generation for hierarchical fuzzy

systems. In NAFIPS ’97. 1997 Annual Meeting of the

North American Fuzzy Information Processing Soci-

ety, pages 444–449, Syracuse, NY, USA.

Hor

cek, P. and Binder, Z. (1997). Hierarchical fuzzy con-

trollers. Annual Reviews in Control, 21:93–101.

Kikuchi, H., Otake, A., and Nakanishi, S. (1998). Func-

tional completeness of hierarchical fuzzy modeling.

Information Sciences, 110:51–60.

Kosko, B. (1997). Fuzzy Engineering. Prentice-Hall Inter-

national, New Jersey.

Lee, M. L., Chung, H., and Yu, F. (2003). Modeling of

hierarchical fuzzy systems. Fuzzy Sets and Systems,

138:343–361.

Raju, G. and Zhou, J. (1993). Adaptive hierarchical fuzzy

controller. IEEE Trans. on System, Man and Cyber-

netics, 23(4):973–980.

Raju, G., Zhou, J., and Kisner, R. A. (1991). Hierarchical

fuzzy control. Int. J. Control, 54:1201–1216.

Wang, L. X. (1998). Universal approximation by hierarchi-

cal fuzzy systems. Fuzzy Sets and Systems, 93:223–

230.

Yager, R. (1993). On a hierarchical structure for fuzzy mod-

eling and control. IEEE Trans. on System, Man and

Cybernetics, 23(5):1189–1197.

Zadeh, L. A. (1996). Fuzzy logic = computing with words.

IEEE Trans. Fuzzy Systems, 4(2):103–111.

Zeng, X. and Keane, J. (2005). Approximation capabili-

ties of hierarchical fuzzy systems. IEEE Trans. Fuzzy

Systems, 13(5):659–672.

MATRIX-BASED HIERARCHICAL FUZZY SYSTEMS