PERFORMANCE EVALUATION

OF A CONTROLLED FLOW-SHOP SYSTEM

WITH A TIMED PETRI NET MODEL

ıc Plassart, Philippe Le Parc, Frank Singhoff, Lionel Marc

Universit

e de Bretagne Occidentale

Laboratoire d’Informatique des Syst

emes Complexes (LISyC)

20, avenue Le Gorgeu – 29285 Brest Cedex, France

Keywords:

Assembly lines, ﬂow-shop, control, performance evaluation, modelling, simulation, Petri nets, industrial case

study.

Abstract:

This paper presents an original performance analysis applied to a ﬂow-shop system driven by a set of local

command units and a central controller. The performance evaluation is done with a timed coloured Petri net

model. Simulation results show needs for bounding the controller response time in order to meet production

targets.

1 INTRODUCTION

During the last few decades the performance increas-

ing of the production systems was mainly based on

an improvement of the device acting directly on the

product ﬂow. However, the behavior of a production

system is also conditioned by the characteristics of

the equipment which ensures its control (Grieco et al.,

2001) .

The control system design of an automated pro-

duction system poses a large amount of hardware and

software problems. They are often complex and bring

into play a more and more consequent amount of data.

This evolution usually implies taking into account the

speciﬁc requirements applied to the reactivity of vari-

ous equipments.

This article presents an industrial case study ap-

plied to a ﬂow-shop system whose control is jointly

ensured by a set of local command units (program-

mable logic controllers) and a central controller. Each

local command unit is located at the production ma-

chine level of the ﬂow-shop and drives an operative

part.

Message exchanges between the local command

units and the controller are carried out several times

during the operating cycle of the production machine.

They are supported by a ﬁeldbus.

In literature, many manufacturing control architec-

tures are identiﬁed (Dilts et al., 1991). They are of-

ten declined in three main types from centralized over

hierarchical to heterarchical control. Our control ar-

chitecture is based on a typical hierachical structure

in which an upper level device coordinates the activi-

ties of a group of lower level devices in a master-slave

manner (Jones et al., 1989). The control ﬂow is typi-

cally top-down and the feedback ﬂow is bottom-up.

In the form of hierarchical architecture, the ex-

changes are always triggered by the upper level de-

vice. But in the present case study, they are initiated

by the local command units. The exchanges are op-

erated according to a request transmission and a re-

sponse reception. The stimulus is then bottom-up and

more than one exchange can be running at the same

time.

Message routing, waiting and processing cumu-

lated delays constitue a response time that is neces-

sary to bound in order to ensure the control system

does not inﬂuence production rates signiﬁcantly.

This study aims to analyze the controller reactivity

to requests sent by local command units and to evalu-

ate its impact on the production system performances.

The article begins by a description of the produc-

tion system and the control architecture in section 2.

The modelling of the ﬂow-shop system and its control

devices are detailled in section 3. It is based on the

formalism of timed coloured Petri nets. The model

performance analysis relates to the message reception

buffer occupancy and controller activity rates. Sev-

eral conﬁgurations are evaluated. The simulation re-

sults summary, presented in section 4, allows to mea-

sure model performances and to analyse the correla-

tion degree between real production systems and their

494

Plassart L., Le Parc P., Singhoff F. and Marcé L. (2006).

PERFORMANCE EVALUATION OF A CONTROLLED FLOW-SHOP SYSTEM WITH A TIMED PETRI NET MODEL.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 494-499

DOI: 10.5220/0001206704940499

 SciTePress

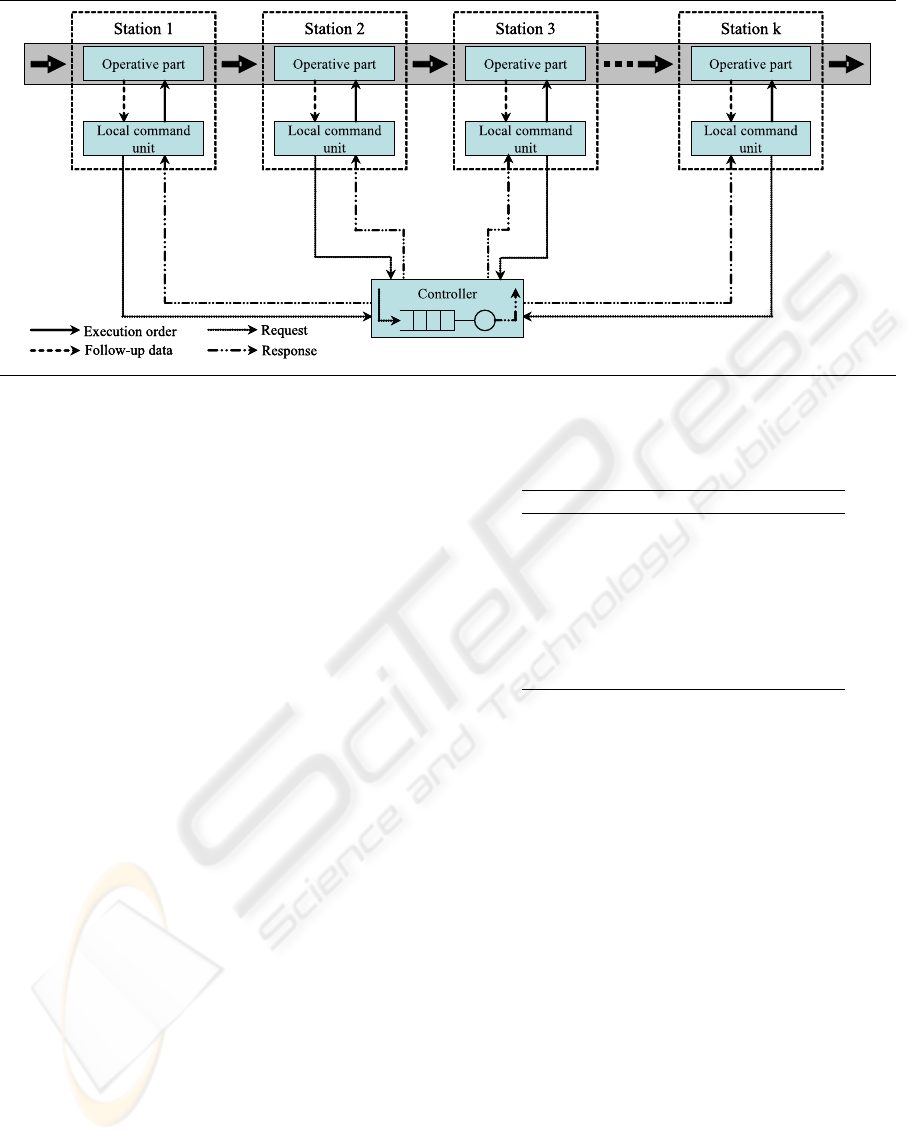
Figure 1: System architecture.

model. Lastly, section 5 presents the conclusions of

our work and a brief description of our future research

in this area.

2 SYSTEM DESCRIPTION

The considered production system is an automated

assembly process with several machines called sta-

tions organized in line. This stucture corresponds to

a ﬂow-shop system in which there is one station at

each stage. The stations work in an independent way

from each other and execute individually their operat-

ing cycle. A station cannot retain and operate more

than one part at a given moment. When a station

is available (no assembly in progress) and a part is

present at its entry, it starts its operating cycle.

The control of the assembly line is ensured by a

central controller which coordinates the various sta-

tions. Thus, it has to be considered as a shared re-

source of the ﬂow-shop system [Fig. 1].

2.1 Operating Cycle of the Stations

During its operating cycle, each station performs

many common operations. For most of them, each

occurence is of constant duration. Only the assembly

processing is of speciﬁc duration. The mean duration

of common operations [Tab. 1] is obtained by mea-

surements done on real production systems.

An operating cycle also includes two waiting

phases of a variable duration due to exchanges with

the controller. A waiting phase corresponds to the

controller response time when it is requested by a lo-

cal command unit. On existing assembly lines, this

Table 1: Operating cycle of a station.

Operation Duration

(ms)

Identiﬁcation 550

Status request 60

Waiting Variable

Status analysis 60

Assembly processing Speciﬁc

Data reporting 60

Waiting Variable

Part relaxation 60

delay is variable and depends of controller load. The

mean waiting time is close to 600 ms.

Parts are transfered from a station to the next one

by a conveyor belt. The conveying time between two

stations is always about 3 000 ms.

2.2 Coordination Function

The local command units request and inform the con-

troller in a regular way to condition and coordonate

their actions. These exchanges proceed at the produc-

tion rate. The controller has an information central-

ization function it enriches by data transmitted by the

local command units and that it can give back.

During an exchange, the local command unit sends

a request to the controller. The message supporting

the request is placed in a communication buffer. The

controller manages the message selection by a FIFO

policy and executes the processing in adequacy with

the message parameters. The latency time in the com-

munication buffer is obviously variable. At the end of

the processing, the controller establishes a response

message that it transmits to the local command unit.

PERFORMANCE EVALUATION OF A CONTROLLED FLOW-SHOP SYSTEM WITH A TIMED PETRI NET

MODEL

495

Conveying

SST

1‘(1,ok)

Identification

SST

Request

SST

Waiting

SSO

Inactivity

LIN

Recording

SST

Parsing

SSS

SST

Transmission

SST

Ack

SST

CycleStarted

MessageSended

@+6

PartIdentified

@+55

DataRecorded

@+60

StatusFound

@+60

CycleReportStatusRequested

StatusReceived

Analysis

SST

PartOK

@+6

[stu = ok]

Process

SST

CycleFinish

@+f(sta)

Reporting

SST

PartNOK

@+6

[stu = nok]

DataReady

@+6

PartComplete

[sta <> n_sta]

Relaxation

SST

AckReceived

Idling

CPU n_cpu‘cpu

Scrap

STA

Shipment

STA

AssemblyFinish

[sta = n_sta]

Controller

Stations

Counting and Reject

Reject

1‘no

REJ

ThresholdReached

Counting

STA

Availability

BUF BUF

BufferEntry

SSS

MessageEntered

MessageAvanced

BufferExit

SSS

MessageLeft

Communication Buffer

StandBy

WIP

n_wip ** WIP

StationEntry

SST

PartReceived

@+300

Conveyor Belt

PartRelaxed

@+6

Finishing

SST

1‘(sta,stu)

1‘(sta,stu,pre) 1‘(sta,stu,pos)

1‘(sta,stu)

if rej = yes

then 1‘(sta,nok)

else 1‘(sta,stu)

1‘(sta,stu)

1‘(sta,stu) 1‘(sta,stu)

1‘(sta,stu)

1‘sta

1‘cpu

if stu = ok

then 1‘sta

else empty

if stu = nok

then 1‘sta

else empty

1‘(sta,stu)

1 ‘n_sta

1‘yes

1‘rej

1‘no

n_rej‘sta

if stu = ok

then 1‘sta

else empty

1‘rej

1‘(sta,stu)

1‘(sta,stu,pre)

1‘(sta,stu,seq)

1‘(sta,stu,pos)

1‘(sta,stu,seq,n_sta)

1‘cpu

1‘(sta,stu,seq)

1‘cpu

1‘(sta,stu,seq,ord)

if ord = 1

then 1‘(sta,stu,seq)

else empty

if ord <> 1

then 1‘(ord - 1)

else empty

1‘ord

if ord > 1

then 1‘(sta,stu,seq,ord -1)

else empty

if sta > 1

then 1 ‘(sta - 1)

else empty

1 ‘sta

if sta = 1

then 1‘(1,ok) ++ 1‘(2,stu)

else 1‘(sta + 1,stu)

1‘(sta,stu)

1‘n_sta

1‘ (sta,stu) 1‘ (sta,stu)

1‘ (sta,stu)

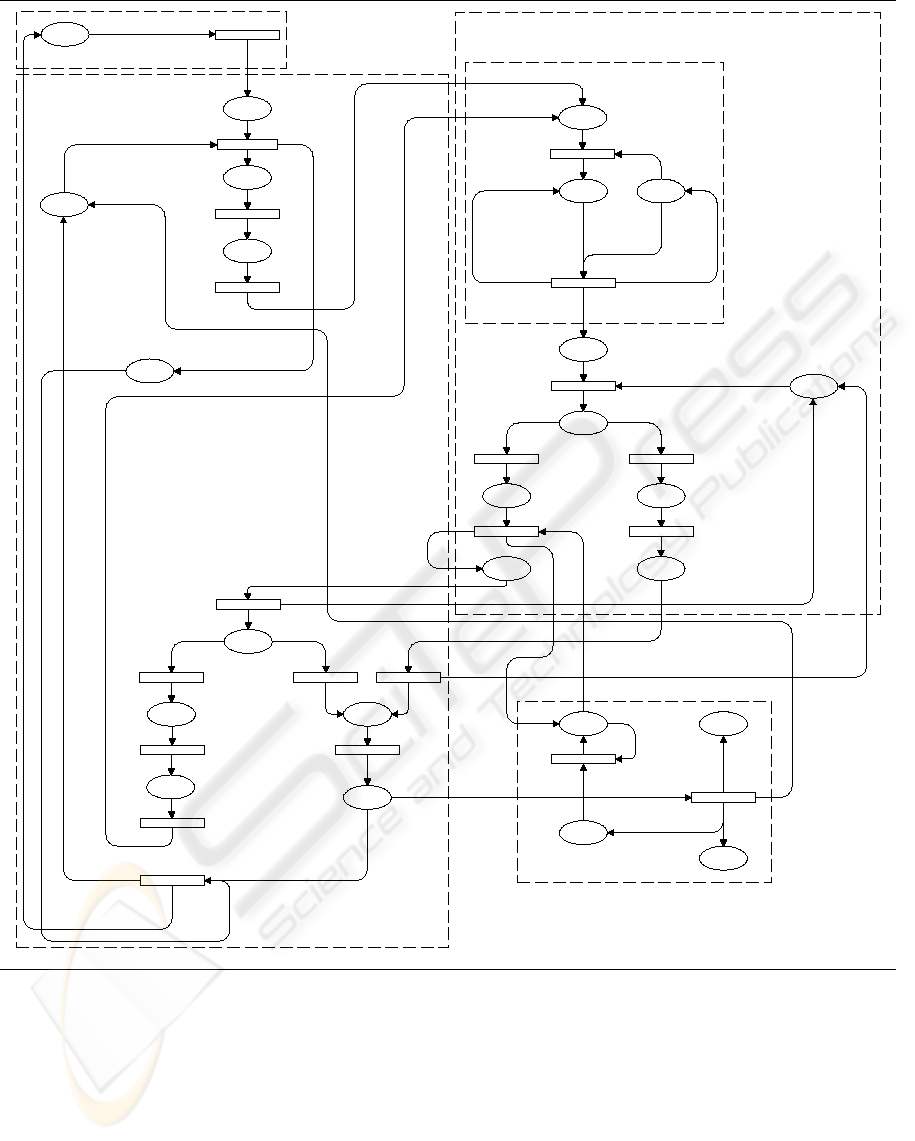
Figure 2: Petri net of the studied system.

A request sent by a local command unit causes a

freezing situation of its cycle. The activity restart

is triggered by the response arrival coming from the

controller.

3 SYSTEM MODELLING

The Petri nets interest for the design and the analy-

sis of production systems has often been empha-

sized (Barad, 1998; Desrochers and Al-Jaar, 1995;

DiCesare et al., 1993). Our model was designed with

that formalism. The timed and coloured extensions

have also been used.

The behaviour of the data processing systems used

in computer-integrated manufacturing and robotics is

ICINCO 2006 - ROBOTICS AND AUTOMATION

496

often based on timed sequences making it possible to

deﬁne the duration of activities. The timed extensions

of Petri nets are highly suitable models for the for-

mal study of these mechanisms (Juanole et al., 2000).

Although timed coloured Petri nets are usually used

to investigate the logical correctness of systems, they

can also be used to evaluate the performances of them.

The Petri net colouring allows to reduce the size of

a model to get a more compact representation of the

systems including dictinct components having simi-

lar behaviours. This is the case here with the station

operating cycle.

The model was designed using the software De-

sign/CPN (Christensen et al., 1997). Our choice has

been guided by the integration of performance facili-

ties in this computer tool (Linstrøm and Wells, 1998).

Design/CPN

allows to collect data during the model

execution and create reports containing statistical val-

ues.

3.1 Modelled Behaviour

This work focuses on the study of interactions within

the control system of an automated assembly line.

Thus, the model describes the architecture supporting

the exchanges between the local command units and

the controller. It is primarily founded on the indepen-

dent activities of the various stations and their access

to a shared resource which is the controller.

The model [Fig. 2] implements three main ele-

ments that are the station set, the communication

buffer and the controller. A counting function of pro-

duced parts is also implemented.

Station operations are integrated into the model in

the form of places. The described sequence takes into

account the operations of routing (place Conveying),

part identiﬁcation (place Identiﬁcation), status request

sent to the controller (place Request), response analy-

sis emitted by the controller (place Analysis), part as-

sembly processing (place Process), production data

reporting (place Reporting) and part relaxation (place

Relaxation).

Transitions correspond to events that make the to-

ken circulation symbolizing the system evolution.

Temporization of some transitions (notation @+de-

lay) makes it possible to keep the presence of tokens

in the places located upstream during the speciﬁed

time. It allows to specify the execution time of op-

erations.

Colouring is primarily used to distinguish various

stations as well as various positions of messages in

the communication buffer.

For the stations, colours are applied according to

their number and their order on the assembly line.

Design/CPN has been replaced by CPN/Tools

Part moving from a station to another one is mod-

elled by incrementing the token colour number, ex-

cept in case of a processing by the last station (end of

assembly). Station availability is managed by a spe-

ciﬁc place (place Inactivity) guaranteeing exclusivity

of its execution to the processing of only one part.

The presence of a token of color x indicates that the

station x is inactive. The place Inactivity is initialized

according to the number of declared stations.

The communication buffer is modelled by a place

(Waiting) in which the token represents the situation

of a station having emitted a request. Colors are af-

fected according to the order in the buffer. Each token

move models a message advance and its color number

is decreased.

The controller disponibility is done by a single

place (place Idling) and a token in this place indi-

cates the controller availability. A message arrival in

the communication buffer implies the token leaves the

place Idling. The controller stops its activity when it

completes the message processing and when the com-

munication buffer is empty.

3.2 Evaluated Criteria

Performance of the studied production systems is

mainly evaluated by the analysis of the communica-

tion buffer occupancy and by the controller load.

Communication buffer contents and the message

origin make it possible to know the number and the

list of stations waiting for a response from the con-

troller.

The message waiting time and the controller re-

sponse time can be deduced from the simulation data.

The analysis of these criteria allows to evaluate pro-

duction system performances and to obtain indica-

tions leading to a good knowledge in the way in which

the exchanges between the local command units and

the controller are held.

Product inter-departure times are also measured.

They are deﬁned as the time between two part com-

plete assemblies and they can be easily compared

with the results of modelled real systems. Product

inter-departure times are a simple and effective per-

formance indicator of the production systems.

3.3 Model Settings

The size of the communication buffer and the ﬁeldbus

speed are two modelling assumptions integrated into

the model.

The size of the communication buffer is deﬁned

according to the number of stations declared in the

model. It makes it possible to have a sufﬁcient capac-

ity for all evaluated conﬁgurations in order to avoid a

saturation in accordance with the real systems.

PERFORMANCE EVALUATION OF A CONTROLLED FLOW-SHOP SYSTEM WITH A TIMED PETRI NET

MODEL

497

The message propagation on the ﬁeldbus is very

fast compared with the modelled system. Only the

latency delays in the communication buffer and mes-

sage processing are signiﬁcant. So, within the frame-

work of our study, we consider that the message trans-

mission is instantaneous.

The temporization of the Petri net places is mainly

deﬁned with mean measurements done on several ex-

isting assembly lines. So, the model is primarily in-

tended for real production system evaluation.

However, the simulation work may also implement

conﬁgurations that are not effective in the workshops.

The assembly processing time cannot be given by

measurements. Then, these durations were gener-

ated using a pseudo-random generator. The genera-

tion takes into account of the maximal and the mini-

mal bounds measured on the existing assembly lines

where the mechanical processing times are between

1 100 and 8 500 ms.

Consequently, the model settings are mainly based

on the number of declared stations and the message

processing time by the controller. The evaluated con-

ﬁgurations differ by the number of stations. The vari-

ous cases go from 2 to 30 stations.

The time sampling rate is generally selected quite

higher than the main time-constant of the controlled

process (Ogata, 1987). The time quanta appointed for

the modelled activities temporization is 10 ms. This

period is deﬁned according to the characteristics of

the local command units whose cycle time is around

60 ms.

Finally, the work-in-progress between two stations

is limited to three parts.

4 SIMULATION RESULTS

The simulation results are declined in two parts. The

ﬁrst phase of our work related to the study of exist-

ing production systems (from 2 to 15 stations). With

these results, we can check the model by comparing

the simulation results with measurements done on real

assembly lines. The second phase is intended to eval-

uate the extension possibilities of the station number

and the potential proﬁts brought by the reduction of

the message processing time.

The model execution time corresponds to a

75 mn manufacturing period sampled every 10 ms

(450 000 clock ticks). It covers the transient and sta-

tionary regimes. The switch from the transient to the

stationary regime is triggered by the assembly end of

the ﬁrst product. However, for homogeneity reason,

we study the stationary regime on the 360 000 last

clock ticks matching with 60 mn of manufacturing.

4.1 Real Systems

Simulation results [Tab. 2] for existing assembly lines

show that the controller load lies between 28 % and

100 %. The saturation point is reached with the 13-

station conﬁguration.

The model execution gives product inter-departure

mean times τ

close to those τ

noted on existing as-

sembly lines.

Table 2: Results for existing systems.

Conf. Contr. load

(%)

Buff. τ

(s)

2 28.4 0.001 8.52 8.65

3 42.5 0.069 8.51

4 56.5 0.104 8.54 8.69

5 67.4 0.264 8.93

7 89.8 0.685 9.48

10 99.7 2.759 12.6

13 100 5.199 16.85 16.28

15 100 6.724 19.6

For conﬁgurations up to 7 stations, the mean buffer

occupancy remains quite lower than one message.

4.2 Prospect

The prospective simulation results show a permanent

controller activity [Tab. 3].

Table 3: Prospective results.

Conf. Contr. load

(%)

Buff. τ

(s)

20 100 10.87 27.36

25 100 13.141 36.68

30 100 16.651 45.64

The report also indicates that the mean buffer oc-

cupancy is between 11 and 17 messages.

4.3 Production Rate Bound

Our simulation results show that product inter-

departure mean time τ

grows with the number of sta-

tions (Little law). By comparing this indicator with

the cumulated time of message processing needed for

assembling one part, we can give a production rate

bound τ

for the modelled assembly lines. In this for-

mula, k is the number of stations and m

is the number

of messages proceed for the station i:

i=1

j=1

ICINCO 2006 - ROBOTICS AND AUTOMATION

498

The production rate τ

obtained by the simulation

approaches but never meets this bound [Fig. 3].

2 4 6 8 10 12 14 16 18 20 22 24 26 28 30

Production rate (s)

Configuration (stations)

Figure 3: Production rate evolution.

For a classical ﬂow-shop system without controller,

the productivity rate τ

is typically ﬁxed by the slow-

est station (Cohen et al., 1983):

= max{t

, t

, ..., t

}

By analyzing the curves, we can give a resulting

production rate bound τ

= max{t

, t

, ..., t

i=1

j=1

}

It corresponds to the worst bound between the one

established by the controller implementation τ

and

the one deﬁned for ﬂow-shop systems τ

5 CONCLUSIONS AND FUTURE

WORKS

The study presented in this article applies to the con-

trol system of automated assembly lines. The aim is to

estimate the impact of the controller implementation

on the production rates. The described analysis en-

ables to evaluate the behaviour and the performances

of the considered production systems.

The modelling and simulation phases show that the

efﬁciency of the assembly lines is strongly linked to

the controller implementation. The production rate

bound ﬁxed by the controller is deﬁned by the mes-

sage processing time. In the case of the cumulated

time of message processing is longer than the operat-

ing cycle time of the slowest machine, the controller

must be seen as the bottleneck station. The need for

limitation of the message processing time to reach the

production targets is then shown.

Our future works are based on two distinct angles.

Firstly, we have to analyze the system with real

network considerations and take into account hybrid

ﬂow-shop systems in which parallel stations are im-

plemented.

Afterwards, we will study speciﬁc message

scheduling policies. Message processing in a FIFO

manner don’t probably correspond to the best way.

We will also evaluate improvements got by message

dispatching on several processors.

REFERENCES

Barad, M. (1998). Timed Petri nets as a veriﬁcation tool.

30th Winter Simulation Conference, pages 547–554.

Christensen, S., Jørgensen, J., and Kristensen, L. (1997).

Design/CPN – A computer tool for coloured Petri

nets. 3rd International Workshop on Tools and Al-

gorithms for Construction and Analysis of Systems,

pages 209–223.

Cohen, G., Dubois, G., Quadrat, J., and Viot, M. (1983).

Analyse du comportement p

eriodique de syst

emes de

production par la th

eorie des dio

ıdes. Rapport de

Recherche n 191 – Institut National de Recherche en

Informatique et Automatique (France).

Desrochers, A. and Al-Jaar, R. (1995). Applications of

Petri nets in manufacturing systems: modelling, con-

trol and performance analysis. IEEE Press.

DiCesare, F., Harhalakis, G., Proth, J., Silva, M., and Verna-

dat, F. (1993). Practise of Petri nets in manufacturing.

Chapman & Hall.

Dilts, D., Boyd, N., and Whorms, H. (1991). The evolution

of control architectures for automated manufacturing

systems. Journal of Manufacturing Systems, 10:79–

93.

Grieco, A., Semeraro, Q., and Tolio, T. (2001). A review

of different approaches to the FMS loading problem.

The International Journal of Flexible Manufacturing

Systems, 13:361–364.

Jones, A., Barkmeyer, E., and Davis, W. (1989). Issues in

the design and implementation of a system architec-

ture for computer integrated manufacturing. Journal

of Computer Integrated Manufacturing, 2:65–76.

Juanole, G., Abdellatif, S., and Gallon, L. (2000). Nou-

veaux concepts sur les transitions du mod

ele RdPTS

: Propri

es dynamiques et attributs temporels dy-

namiques. 1

ere Conf

erence Internationale Francoph-

one d’Automatique (CIFA’2000), pages 976–981.

Linstrøm, B. and Wells, L. (1998). Simulation based perfor-

mance analysis in Design/CPN. Workshop on Practi-

cal Use of Coloured Petri nets and Design (CPN’98),

pages 117–130.

Ogata, K. (1987). Discrete-time control systems. Prentice-

Hall International Editions.

PERFORMANCE EVALUATION OF A CONTROLLED FLOW-SHOP SYSTEM WITH A TIMED PETRI NET

MODEL

499