EYE AND GAZE TRACKING ALGORITHM FOR

COLLABORATIVE LEARNING SYSTEM

Djamel Merad

LIRIS laboratory

Stephanie Metz

ICAR Laboratory

Serge Miguet

LIRIS Laboratory

Keywords:

Head tracking, Pattern recognition, Machine vision.

Abstract:

Our work focuses on the interdisciplinary ﬁeld of detailed analysis of behaviors exhibited by individuals dur-

ing sessions of distributed collaboration. With a particular focus on ergonomics, we propose new mechanisms

to be integrated into existing tools to enable increased productivity in distributed learning and working. Our

technique is to record ocular movements (eye tracking) to analyze various scenarios of distributed collabora-

tion in the context of computer-based training. In this article, we present a low-cost oculometric device that

is capable of making ocular measurements without interfering with the natural behavior of the subject. We

expect that this device could be employed anywhere that a natural, non-intrusive method of observation is

required, and its low-cost permits it to be readily integrated into existing popular tools, particularly E-learning

campus.

1 INTRODUCTION

The principle of the oculometry is to measure the po-

sition and orientation of the eye of a subject as he

looks at a computer monitor. A software program,

which knows what is displayed on the monitor at what

particular instant, is able to determine what the sub-

ject had been looking at for any speciﬁed instant. For

many years, this technique has been used by psychol-

ogists to study behavioral responses to images, but

more recently, it has spread other domains such as

that of ergonomicists and Web masters. (Duchowski,

2002) provides an excellent survey of eye tracking ap-

plications in several information processing tasks. In

the case of analysis of the relationship between image

observation and cognitive response, we can quote for

example: the inspection of visual scenes (Henderson

and Hollingworth, 1998), visual Inspection (Reingold

et al., 2002), industrial engineering and human fac-

tors (Anders, 2001). But in the last few years, this

technique has been applied to determine the usabil-

ity of Web, and to determine why some web sites are

more effective than others (Sibert and Jacob, 2000).

This is a direct consequence of the development of

information technologies and communication.

Our work will relate to ﬁnd precise oculometric

indicators that manifest during distributed computer

based training. We prescribe a control environment

where two geographically dispersed interlocutors en-

gaged in collaborative work via face-to-face video

conferencing. Each interactive station has a camera

that captures images of the subject’s faces and eyes

as movements occur and words are spoken. As the

collaboration progresses, we collect indicators which

will allow us to know, for each instant, what is con-

sulted by the interlocutors and for what type of inter-

actions. Thus, it will be necessary to synchronize the

verbal interactions with the glances of the subjects at

each instant of collaborative activity.

Previous work (A.Corbel et al., 2003), (Baker et al.,

2002) have made it possible to enumerate the types of

interactions observed at the instances during collabo-

ration using tools that allow the mutual construction

of a common conceptual representation of the subject

matter being discussed by the collaborators. In addi-

tion, tools that facilitate this type of activity have been

developed. In particular, DREW makes it possible to

collaborate and jointly synthesize knowledge through

primitives such as the catalogue, white board, a text

tool, an argumentative graph. These various studies

are based on the analysisof verbal corpora (catalogue)

and argumentative graphs. They do not make it pos-

326

Merad D., Metz S. and Miguet S. (2006).

EYE AND GAZE TRACKING ALGORITHM FOR COLLABORATIVE LEARNING SYSTEM.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 326-333

DOI: 10.5220/0001207503260333

 SciTePress

sible to pin-point the speciﬁc events that initiate an

interaction for mutual knowledge dissemination. In-

deed, the interlocutor does not always refer verbally

to the information which enabled him to ﬁnd such so-

lutions. So if the ultimate goal is to help the interlocu-

tors in their collaboration, it is necessary to character-

ize the chronological process of mutual transfer and

assembly of knowledge. For example, if one notes by

oculometry that an interlocutor seeks information on

the screen to argue, it would seem most appropriate

that assistive action would immediately present this

information centrally on the screen (ﬁgure 1).

Figure 1: collaborative task.

Several techniques to determine what assistive ac-

tion to take during the follow-up of a glance exist.

During last decades, these techniques gained much

in precision, which makes their ﬁelds of application

very broad. On the other hand, no instrument can be

perfect in a situation where none satisﬁes all the re-

quirements.

We can classify the techniques currently developed

in three groups, according to the degree of contact

with subject (Collewijn, 1999), (Glenstrup and Niel-

son, 1995).

• Techniques based on the reﬂection of a luminous

ray on the cornea.

• Techniques based on the application of a special

contact lens.

• Techniques of electro-oculography.

We point out that tools based on corneal oculomet-

ric reﬂection are the most used. These techniques are

those which present more comfort to the subjects, do

not require the presence of specialists (ophtalmolo-

gist) and, under good experimental conditions, give

precise results. We ﬁnd on the market two types

of systems using corneal reﬂection: oculometer with

helmet (camera placed on the head) and oculome-

ter without helmet (camera placed on the monitor).

The oculometer with helmet is largely used because it

is adaptable and usable in several situations (reading

on dashboard, reading on monitor, subject moving...).

For this reason, practically all the companies have de-

veloped a model whose general principle is the same.

However for our purposes, we will not be able to use

this apparatus because the helmet is not comfortable

and will obviously interfere with the subject.

The oculometer without helmet makes it possible

to track in real time the movements of the eye using a

light-emitting diode (LED) coupled with camera de-

vice placed under the monitor. This tool is especially

adapted to work on computer displays. The ﬁrst ap-

paratus of this type uses a head-rest to limit the ﬁeld

of movement of this one. This constraint makes difﬁ-

cult its use for long-lasting experiments, as it results

in muscle fatigue. More recently we have seen pas-

sive devices that make no contact with the subject.

After seeing several demonstrations of these de-

vices, we have concluded that the most successful

is Tobbii. This apparatus has the advantage of be-

ing fast and easy to use and, more importantly, does

not place signiﬁcant restrictions on the movements of

the subject during collaboration. However it is cost-

prohibitive, limiting its use as a general-purpose tool.

In short, several kinds of commercial products ex-

ist. These products are generally highly accurate and

reliable; however all require either expensive hard-

ware or artiﬁcial environments (cameras mounted on

a helmet, infrared lighting, etc). The discomfort and

the restriction of the motion affects the person’s be-

haviour, which therefore makes it difﬁcult to measure

his/her natural behaviour. These limitations make

them unsuitable for our purpose. We have sought to

create a device that removes these limitations.

2 PROPOSED METHOD

The objective of our study is to correlate the men-

tal representation of exchanged information with the

verbal interactions that occur as the representation is

built. The oculometry must give indications on the

representations of each instant, and show the step-by-

step progression of development of the representation

as the collaboration proceeds.

First, we analyzed the most popular oculometric.

We noted the difﬁcult problems to which they are

faced and that still have not been solved in a satis-

factory manner. We established that in the best con-

ditions, the system to develop must submit to the fol-

lowing requirements:

• No not hinder the head (or the body) movement.

• Not requires a direct contact with the user: nor hel-

met, nor lentils.

EYE AND GAZE TRACKING ALGORITHM FOR COLLABORATIVE LEARNING SYSTEM

327

• An affordable price.

• Good eye gaze localization.

• Enable a large vision ﬁeld.

• Real time response.

• To be easy to use on a large palette of users.

• To be easily usable by the scientist and the user.

To solve this problem, much research has been di-

rected to non-intrusive gaze tracking in the past few

years (Wu et al., 2005), (Wang et al., 2003), (Zhu

and Yang, 2002), (Matsumoto and Zelinsky, 2000),

(Pastoor et al., 1999), (Kim and Ramakrishna, 1999),

(Toyama, 1998), (Stiefelhagen and Yang, 1997),

(Pomplun et al., 1994), (Baluja and Pomerleau, 1994).

These systems fall into two categories: analytical ap-

proaches and neural network approaches. A neu-

ral network based approach takes eye images as in-

put and learns patterns from examples. The reason

why they can achieve a higher accuracy is that they

take advantage of the pixel intensity information of

the whole eye image. Although neural network sys-

tems have achieved higher accuracy in ofﬂine evalua-

tions, few systems have been applied to real applica-

tions, because the trained neural network is too sensi-

tive to changes in users, lighting conditions, and even

changes within the user.

An analytical gaze estimation algorithm employs

the estimation of the visual direction directly from the

eye features such as irises, eye corners, eyelids, etc to

compute a gaze direction. If the positions of any two

points of the nodal point, the fovea, the eyeball center

and the pupil center can be estimated, the visual direc-

tion is determined. However, those points are hidden

in eyeball thus they will not be viewable without some

special equipment. The approach to solve this prob-

lem is to estimate the eyeball center from other view-

able facial features indirectly. These methods assume

that the eyeball is a sphere and the distances from the

eyeball center to the two eye corners is known (gen-

erally ﬁxed to 13 mm). The eye corners are located

(for example by using a binocular stereo system) and

are then used to determine the eyeball center. They

also assume that the iris boundaries show circles in

the image and use Hough Transformation to detect

them. The center of the circular iris boundary is used

as the pupil center.

The drawback of these methods is the fact that the

eye model used is simplistic and is not adapted to all

persons. It is easy to see that the eyeball form is not a

sphere and it’s different for each person, also for sev-

eral pathological reasons (myopia, longsightedness,

...), the optic axis doesn’t pass by the eyeball center.

In this kind of methods, the accurate determination of

the eyeball center is very important. For example, if

the eyeball center is detected at 1mm from the real

position assuming that the eye radius is 13 mm, we

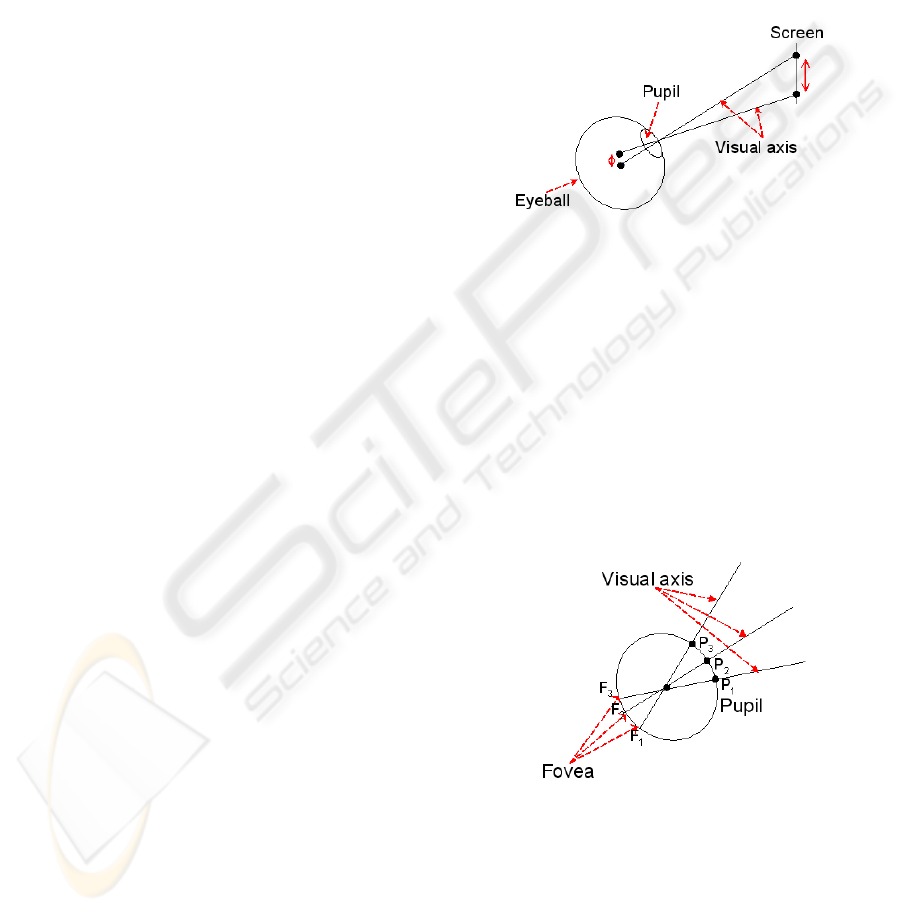
will ﬁnd on a screen placed to 1m, an errors of 76.9

mm (ﬁgure 2).

Another drawback of this approach is the fact that

the accuracy of gaze tracking is greatly depends upon

the detection of the eye corners. For some people the

detection of corners is not made correctly because of

the eyelid form. Another difﬁcult problem is the fact

that on particular head positions (with regard to cam-

era), the internal corner of the eye is occluded by the

nose, therefore eye gaze direction is not determined.

Figure 2: Error propagation.

For these reasons, we proposed to develop an

oculometer by a stereoscopic vision system without

eye corners detection. We determine the visual

direction by estimating the 3D position of the pupil

center named P by stereovision triangulation and the

eyeball center named C by an oculometric calibration

procedure exposed in section 2.1. We assume that

when changing the eye gaze, the eyeball rotates

around its center and this center is ﬁxed with regard

to the head (ﬁgure 3).

Figure 3: Assumption.

The principle of this device presented in the ﬁg-

ure 4 consists ﬁrst in tracking the user head, followed

by the 2D eye zone localization. From this area, we

apply simple image processing in order to track the

pupil. The oculometric calibration enables us to ﬁnd

the 3D eyeball center with respect to the head refer-

ence and ﬁnally, the intersection of the line formed by

ICINCO 2006 - ROBOTICS AND AUTOMATION

328

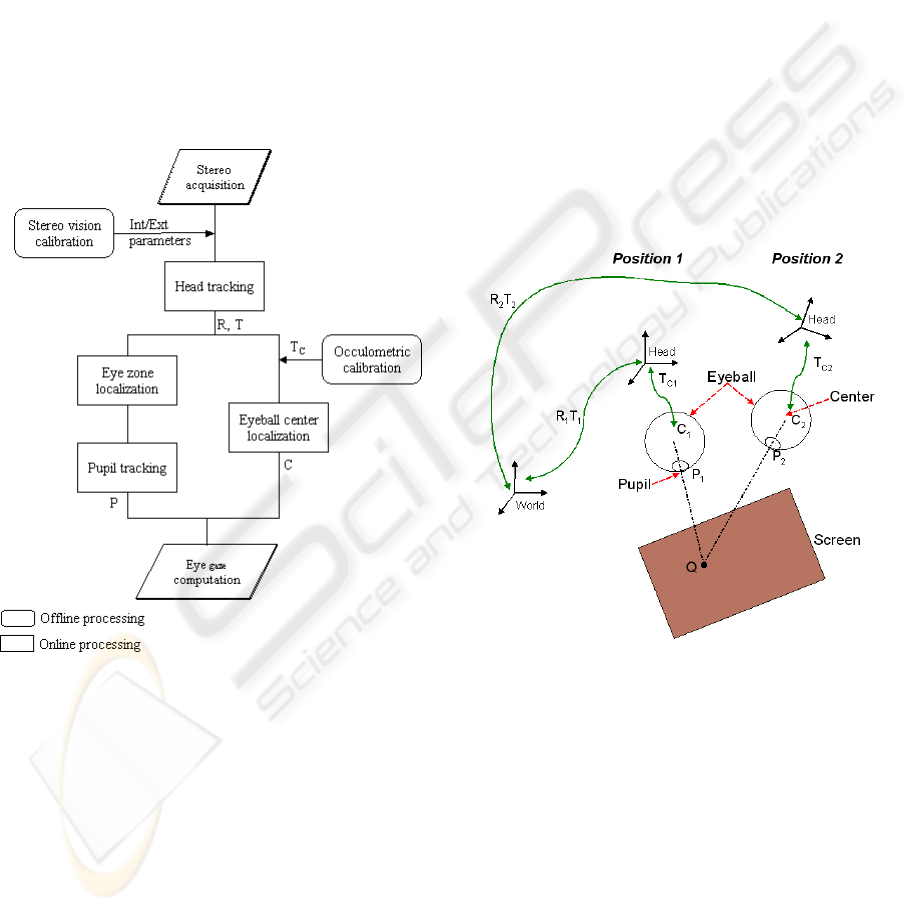
CP and the plan formed by the screen determines the

gaze point.

Head position is computed in real time by stereovi-

sion and while using some coded targets. This stage

is retailed in section 2.2 and the 3D pupil tracking is

described in paragraph 2.3.

In our system all localization measures are made

by a binocular system. We calibrated the two cameras

by Zhang’s method (Zhang, 1999). We obtained the

intrinsic and extrinsic parameters of each camera and

the left/right camera rigid transformation. The advan-

tage of using two cameras for eye tracking instead of

only one is that the absolute 3D position of the dif-

ferent features can be easily and precisely determined

by stereo matching of the characteristic points of both

eyes in the images.

Figure 4: Proposed Method.

2.1 Oculometric Calibration

The goal of this procedure is to determine the rigid ge-

ometric transformation (translation and rotation) en-

abling to ﬁnd the position of the eyeball center C in

relation to the head landmark. This transformation is

only a translation T

For this procedure (ﬁgure 5), we know the 3D posi-

tion of a point Q on the screen as well as the 3D pupil

position with regard to a landmark associated to the

scene (world landmark). Moreover, we also compute

head/world transformation. One asks the user to stare

at a point on the screen, then we calculate world/head

transformation R

and we determine the 3D pupil

position/world landmark P

The user moves the head and stare at the same

point, we determine the second world/head transfor-

mation R

and we compute the second 3D pupil

position P

. We get the following equations :

Collinearity constraints:

= k

− Q) + Q (1)

= k

− Q) + Q (2)

We have also the following transformations:

= R

∗ T

+ T

(3)

= R

∗ T

+ T

(4)

We obtain an over-determined system with 12

equations and 11 unknown that we solve by the least

square method. Theoretically, we need only 1 point

and 2 head positions to localise the eyeball center, but

in practice and in order to improve the accuracy we

should take several points (or head positions).

Figure 5: Oculometric calibration.

2.2 Head Tracking

Many methods enabling real-time object pose compu-

tation in relation to the camera exist in the literature.

In the approach used for this application, the intrinsic

camera parameters are assumed to be known. In addi-

tion, the method requires ﬁnding the correct matching

between a set of 3D scene points and a set of 2D im-

age points. Thus, image features must be extracted.

Depending on the objective to reach and the pro-

cessing to apply on them, image features may be of

a very different nature. We can distinguish two main

families of image feature extraction approaches:

EYE AND GAZE TRACKING ALGORITHM FOR COLLABORATIVE LEARNING SYSTEM

329

- approaches which are based on searching a known

target in the scene,

- approaches which look for speciﬁc geometrical

primitives on the object to track.

Because of the hard constraint on computation time

in our context, we choose the ﬁrst type of methods.

Indeed, instead of trying to recognize an object of the

real world, we prefer to detect the targets positioned

on it. Image processing algorithms can be optimized

for the detection of these targets of known geometry.

In addition, coded targets may contain speciﬁc fea-

tures which enable ﬁnding the semantic relationship

between observed objects and the a priori knowledge

about the real world.

Coded targets are widely used in augmented real-

ity systems. One of pioneering systems is the so-

called Matrix system proposed by Rekimoto (Reki-

moto, 1998), renamed later Cybercode (Rekimoto

and Ayatsuka, 2000). ARToolkit (Kato et al., 2000),

(Kato and Billinghurst, 1999) is a library which en-

ables rapidly creating augmented reality applications.

Unfortunately, performances of this freeware sys-

tem

have to be improved. For this reason, research

laboratories have developed their own applications

as ARTag (Fiala, 2005) which look like ARToolkit

much. InterSense society (Naimark and Foxlin, 2002)

has also developed its system coded target based sys-

tem. The later uses circular targets instead of square

targets generally used in prior systems. This system

was not the ﬁrst one ((Cho and Neumann, 1998) de-

veloped a similar one in 1998) but it is considered as

the most performing.

Our goal is to rapidly and accurately detect and

localize the user head. That is why we opted for a

square target based system.

The processes used to achieve head detection and

localization are the following:

- contrast enhancement,

- image binarization,

- connex components analysis for black image area

detection,

- high curvature points detection,

- point index reading using white points of the target

corners,

- matching target corners which have the same in-

dex,

- head pose computation.

Some results are represented in the ﬁgure 6, where

the head landmark and the eye region are superim-

posed in the image.

http://www.hitl.washington.edu/artoolkit/

Figure 6: Head and eye tracking.

2.3 Pupil Tracking

The eye gaze determination algorithm cited above as-

sumes that the iris boundaries show circles in the im-

age and used Hough Transformation to detect them

(after edge detection). The center of the circular iris

boundary was used as the pupil center.

We have tried to use the same procedure and we

got some bad results, therefore we can state that this

approach has several drawbacks:

- In a natural behavior the eye is naturally mid

closed, it is then more difﬁcult to detect a circle

from iris edge.

- Eye images available for gaze tracking are typically

small in size. Thus the number of available iris

edge points is usually very limited, therefore the

vote procedure of Hough transform is not appro-

priated.

- The diameter of an iris is often assumed to be

known, while it obviously varies from person to

person, and varies when the distance between the

user and the camera changes.

- For a large range of gaze directions, the iris in an

image cannot be well approximated by a circle (it

is an ellipse), other authors use Hough transform to

approximate the ellipse but we think that the previ-

ous problems still remain.

To detect and localise accurately the pupil in the

image, we start by some image processing. We en-

hance the contrast contour and smooth the homoge-

nous regions by an anisotropic diffusion algorithm

(Perona and Malik, 1990). Because of the high con-

trast between the iris and the eye white, the eye image

is easily binarised based on a threshold. Afterwards,

we search the connected objects in the binarised im-

age and compute its centroid. To reﬁne this detection,

we can use the epipolar constraint and ﬁnally, by tri-

angulation we compute the 3D pupil position. Figure

7 shows respectively: original frame, eye zone im-

age and its segmentation and ﬁnally the pupil locali-

ICINCO 2006 - ROBOTICS AND AUTOMATION

330

Figure 7: Pupil Tracking.

sation. In this example, hough transform is not able

to localise the iris.

3 EXPERIMENTAL RESULTS

In order to test the performance of our algorithm for

visual direction estimation in a real-time gaze track-

ing system, we have made some experiments using

several real face image sequences. Also, to investigate

the accuracy, we have made experiments in a known

environment.

There were four markers placed on the four cor-

ners on the screen. We take the 3D coordinates of

the four markers as the reference coordinates for the

true point-of-regard. The errors of the algorithm are

computed by comparing the estimated point-of-regard

and the reference coordinates. Video cameras were

placed at the top of the screen and input image size

was 320 × 240 pixels. The person sits 0.65m away

from the camera pair; in this conﬁguration the user

has enough space for free movement. The horizontal

distance between markers was 29cm and the vertical

distance was 22.5cm (screen 14in). We ask the sub-

ject to stare at a marker on a desktop screen using his

gaze while moving the head (rotation, translation).

Figure 8 shows some images obtained in a real-time

gaze detection experiment. The 3D gaze vectors are

superimposed on the tracking result, the low-right im-

age represent a degenerated case. The whole process

including face tracking and gaze detection takes about

83 ms, thus the 3D point-of-regard can be determined

at 13Hz.

Errors of these algorithms performance on four dif-

ferent sequences are listed in ﬁgure 9, ﬁgure 10, ﬁg-

ure 11, ﬁgure 12 corresponding respectively to mark-

ers 1 to 4. We can see the average error of point-of-

regard is less than 3cm for the Marker 1; this marker

is used in oculometric calibration process. The sec-

ond upper marker the average error of point-of-regard

is less than 4.2cm and the two lower markers the av-

erage errors are less than 5.9cm. However, we did

Figure 8: Eye gaze detection.

not take into account the degenerated cases (Marker1

≈ 14%, Marker2 ≈ 18%, Marker3 ≈ 23%, Marker4

≈ 21%,). Indeed, during the tracking process, our al-

gorithm sometimes loses the head or the pupil and in

those cases, we get outliers.

Figure 9: Point-of-regard error of the marker 1.

We also noticed that in our method as in other

analytical approaches, the accuracy of gaze tracking

greatly depends upon the resolution of the eye im-

ages. Suppose that the size of an eye image is 35×25,

which is a situation when the person is from 65 cm to

the screen, the range of the pupil movement is then

about 16 pixels. Let’s consider our method of cal-

culating the gaze direction (ﬁgure 13). In the ﬁgure,

|l| ∈ [0, 8] pixels, r ≈ 20 pixels. The smallest level

unit of l is |∆l| = 1 pixel. Then,

θ = arcsin l/r

∆θ ≈

∂θ

∂l

∆l +

∂θ

∂r

∆r (5)

1 − (l/r)

∆l −

1 − (l/r)

∆r

Supose ∆r = 0, then for |l| ∈ [0, 8] pixel, |∆θ| =

[2.86

◦

, 3.41

◦

]. Thus, the smallest unit of θ, i.e. the

resolution of gaze direction is about 3.2

◦

. If the iris

EYE AND GAZE TRACKING ALGORITHM FOR COLLABORATIVE LEARNING SYSTEM

331

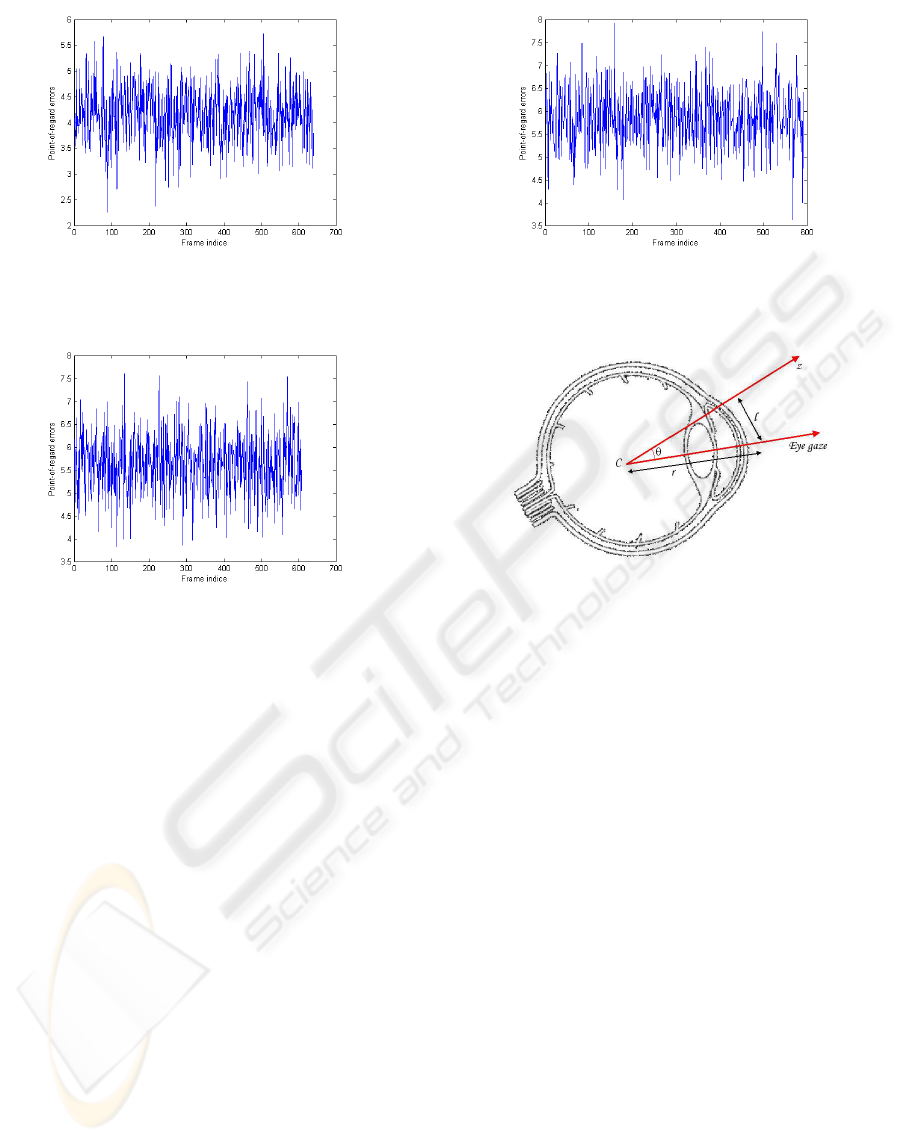
Figure 10: Point-of-regard error of the marker 2.

Figure 11: Point-of-regard error of the marker 3.

detection has a small error of 1 pixel, it will gener-

ate a tracking error of about 3.2

◦

of gaze direction.

Therefore, it is hard to determine the gaze in a 3D

scene accurately with such low resolution, neverthe-

less in our use we only need to determine a region in

the screen.

4 CONCLUSION

In this paper, a real-time implementation of a new

method to estimate gaze direction using stereo vision

is proposed. The motivation of our approach is to de-

velop a low-cost device allowing to estimate the eye

gaze robustly in real-time and with satisfactory ac-

curacy. The ﬁrst originality of our algorithm is the

use of the target in order to recognize, localize and

ﬁnally to quickly track the head of all persons. Also

by using the described ”oculometric calibaration” de-

scribed, we were able to discard other features detec-

tion and obtain a proper eyeball center. Because of

this, our method is adapted to different person and the

accuracy of the visual direction should not be affected

by the change of head pose. In summary, we devel-

oped a low-coast system (only two webcams) which

Figure 12: Point-of-regard error of the marker 4.

Figure 13: Image resolution problem.

observes a person without giving him/her any discom-

fort and shortly, this system will be applied for the

collaborative tasks survey.

Currently, our algorithm is coded with Matlab and

we got a satisfactory execution speed (13Hz), in our

future work; we will increase processing speed of the

system by using C++. We also aim to improve the

accuracy by using high resolution camera and other

image processing tools to detect the pupil (not the iris

center).

REFERENCES

A.Corbel, P.Jaillon, Serpaggi, X., Baker, M., Quignard,

M., Lund, K., and Sjourn, A. (2003). A drew: Un

outil internet pour crer des situations d’apprentissage

cooprant. In Environnements Informatiques pour

l’Apprentissage Humain (EIAH 2003), Strasbourg,

France.

Anders, G. (2001). Pilots attention allocation during ap-

proach and landingeye- and head-tracking research in

an a330 full ﬂight simulator. In International Sympo-

sium on Aviation Psychology (ISAP).

Baker, M., Lund, K., and Quignard, M. (2002). Multi-

representationnal argumentative interactions : the case

of computer-mediated communication in cooperative

ICINCO 2006 - ROBOTICS AND AUTOMATION

332

learning situation. In Proceedings of the Fifth Inter-

national Conference of the International Society for

the Study of Argumentation (ISSA’02), Sic Sat, Ams-

terdam.

Baluja, S. and Pomerleau, D. (1994). Non-intrusive gaze-

tracking using artiﬁcial neural networks. In Neural

Information Processing Systems, Morgan Kaufman

Publishers, New York.

Cho, Y. and Neumann, U. (1998). Multi-ring color ﬁducial

systems for scalable ﬁducial tracking augmented real-

ity. In Proceedings of the Virtual Reality Annual In-

ternational Symposium (VRAIS98), page 212, Wash-

ington, DC, USA.

Collewijn, H. (1999). Multi-representationnal argumenta-

tive interactions : the case of computer-mediated com-

munication in cooperative learning situation. In H. S.

Carpenter and J.G.Robson [Eds.], Vision Research:

A practical Guide to Laboratory Methods, pages 245–

285, Oxford: Oxford Univ. Press.

Duchowski, A. T. (2002). A breadth-ﬁrst survey of eye

tracking applications. In Behavior Research Methods,

Instruments, and Computers.

Fiala, M. (2005). Artag, a ﬁducial marker system using digi-

tal techniques. In Proceedings of the 2005 IEEE Com-

puter Society Conference on Computer Vision and

Pattern Recognition (CVPR05), Volume 2, pages 590–

596, Washington, DC, USA.

Glenstrup, A. and Nielson, T. (1995). Eye controlled media

: Prensent and future state. In Masters thesis, Univer-

sity of Copenhagen.

Henderson, J. M. and Hollingworth, A. (1998). Eye

movements during scene viewing: An overview. In

G.Underwood (Ed.), Eye Guidance in Reading and

Scene Perception.

Kato, H. and Billinghurst, M. (1999). Marker tracking and

hmd calibration for a video-based augmented reality

conferencing system. In Proceedings of the 2nd IEEE

and ACM International Workshop on Augmented Re-

ality (IWAR99), pages 85–92, Washington, DC, USA.

Kato, H., Billinghurst, M., Poupyrev, I., Imamoto, K., and

Tachibana, K. (2000). Virtual object manipulation on

a table-top ar environment. In Proceedings of the In-

ternational Symposium on Augmented Reality (ISAR

2000), pages 111–119, Munich, Germany.

Kim, K. and Ramakrishna, R. (1999). Vision-based eye-

gaze tracking for human computer interface.. In Inter-

national Conference on Systems, Man, and Cybernet-

ics, pages 324–329.

Matsumoto, Y. and Zelinsky, A. (2000). An algorithm for

real-time stereo vision implmentation of head pose

and gaze direcetion measurement. In International

Conference on Automatic Face and Gesture Recogni-

tion, pages 499–504.

Naimark, L. and Foxlin, E. (2002). Circular data ma-

trix ﬁducial system and robust image processing for

a wearable vision-inertial self-tracker. In Proceedings

of the International Symposium on Mixed and Aug-

mented Reality (ISMAR02), pages 27–36, Washing-

ton, DC, USA.

Pastoor, S., Liu, J., and Renault, S. (1999). An experimen-

tal multimedia system allowing 3-d visualization and

eyecontrolled interaction without user-worn devices.

In IEEE Trans. Multimedia, 1(1), pages 41–52.

Perona, P. and Malik, J. (1990). Scale-space and edge de-

tection using anisotropic diffusion. In IEEE Transac-

tions on pattern and machine intelligence. Vol 12. NO.

7, pages 629–639.

Pomplun, M., Velichkovsky, B., and Ritter, H. (1994).

An artiﬁcial neural network for high precision eye

movement tracking. In B. Nebel and L. Drescher-

Fischer (Eds.), Lectures Notes in Artiﬁcial Interlli-

gence, Springer Verlag, Berlin.

Reingold, E. M., Charness, N., Pomplun, M., and Stampe,

D. M. (2002). Visual span in expert chess players:

Evidence from eye movements. In Psychological Sci-

ence.

Rekimoto, J. (1998). Matrix : A realtime object identiﬁca-

tion and registration method for augmented reality. In

Proceedings of the Third Asian Paciﬁc Computer and

Human Interaction (APCHI98), page 6368, Washing-

ton, DC, USA.

Rekimoto, J. and Ayatsuka, Y. (2000). Cybercode : de-

signing augmented reality environments with visual

tags. In Proceedings of DARE 2000 on Designing aug-

mented reality environments (DARE00), pages 1–10.

Sibert, L. E. and Jacob, R. J. (2000). Evaluation of eye gaze

interaction. In Human Factors in Computing Systems:

CHI 2000 Conference Proceedings. ACM Press.

Stiefelhagen, R. and Yang, J. (1997). Gaze tracking for mul-

timodal human-computer interaction. In International

Conference on Acoustics, Speech, and Signal Process-

ing, pages 2617–2620.

Toyama, K. (1998). Look, ma . no hands!. hands-free cursor

control with real-time 3d face tracking. In Workshop

on Perceptual User Interfaces.

Wang, J. G., Sung, E., and Venkateswarlu, R. (2003). A eye

gaze estimation from a single image of one eye. In

Proceedings of the Ninth IEEE International Confer-

ence on Computer Vision (ICCV 2003) 2-Volume.

Wu, H., Chen, Q., and Wada, T. (2005). Visual direction

estimation from a monocular image. In IEICE Trans.

Inf. and Syst., Vol. E88D, No.10., pages 2277–2285.

Zhang, Z. (1999). Flexible camera calibration by viewing

a plane from unknown orientations. In IEEE Interna-

tional Conference on Computer Vision.

Zhu, J. and Yang, J. (2002). Subpixel eye gaze tracking.

In IEEE International Conference on Automatic Face

and Gesture Recognition.

EYE AND GAZE TRACKING ALGORITHM FOR COLLABORATIVE LEARNING SYSTEM

333