LINEAR QUADRATIC GAUSSIAN REGULATORS FOR

MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS

L. Armesto and J. Tornero

Dept. of Systems Engineering and Control, Technical University of Valencia,

Camino de Vera s/n 46022, Valencia, Spain

Keywords:

Multi-rate Sampled Data Systems, Linear Quadratic Regulator, Kalman Filter.

Abstract:

In this paper, linear quadratic Gaussian regulators are presented and formalized for multi-rate sampled-data

stochastic systems using two well-known approaches: lifting technique and time-variant periodic modeling. It

has been demonstrated that both regulators are equivalent at the global frame-period with different computa-

tional costs and execution periods. An interesting analysis has been done to demonstrate the convergence of a

periodic Kalman ﬁlter, used in the periodic regulator, into its equivalent continuous one (Bucy Kalman ﬁlter),

when the periodicity ratio converges to inﬁnity. In addition to this, in both regulators, multi-rate holds have

been used, acting as interfaces between signals at different sampling rates, which may improve the system

performance. A numerical example of LQG multi-rate control of a MIMO plant shows the application of both

regulators, where in addition to showing the improvement with respect to the single-rate case.

1 INTRODUCTION

In complex real-time control systems, it becomes

more and more realistic to assume different sampling

periods for different system variables. This is the case

of many distributed control systems, where there are

more than one processor and many communication

channels involved. Moreover, sensor and actuators

with different dynamics should be treated at different

rates. For all these situations, multi-rate techniques

may be used to improve system performances.

In multi-rate sampled-data systems, inputs and out-

puts are updated at different sampling rates. In most

of the cases, multi-rate sampling is due to technolog-

ical limitations in sensors and actuators. Other lim-

itations may come from computational requirements

in real-time applications such as multi-rate sensor fu-

sion, data-missing, mapping, etc.

A general multi-rate sampling could be asynchro-

nous and totally random, although it is generally ac-

cepted that a periodicity between sampling-rates of

inputs and outputs exists. On the one hand, the m

inputs are updated at T

, with v = 1, 2, . . . , m; on

the other hand, the p outputs are sampled at T

with w = 1, 2, . . . , p. The frame-period is for-

mally deﬁned as

T = lcm(T

, T

) which involves

all input and output periods, and the base-period is

T = gcd(T

, T

). The ration between periods is

N =

T /T , where N is the periodicity of the system.

Therefore, inputs and outputs are updated/sampled at

multiple time instants of the base-period, with T

·T and T

·T .

The multi-rate problem has been extensively

treated in the last four decades and it is possible

to ﬁnd many contributions dealing with modeling

and analysis (Albertos, 1990; Araki and Yamamoto,

1986; Godbout et al., 1990; Khargonekar et al., 1985;

Tornero, 1985; Tornero and Armesto, 2003; Tornero

et al., 1999), as well as control design of multi-rate

systems (Chen and Francis, 1995; Colaneri and de

Nicolao, 1995; Qui and Chen, 1999; Tangirala et al.,

1999). One of the approaches to treat the modeling

phase is to assume an enlarged MIMO system (Khar-

gonekar et al., 1985; Albertos, 1990; Araki and Ya-

mamoto, 1986; Godbout et al., 1990). In these ap-

proaches, a discrete time-invariant state equation ex-

pressed at frame period

T is used, with enlarged in-

put and output vectors. Many of these modeling tech-

niques are based on the initial idea of VSD (Kranc,

1957). In (Tornero, 1985), Tornero proposed an in-

teresting time-variant modeling technique for multi-

rate systems expressed at base-period T , based on two

auxiliary state vectors associated to inputs and out-

puts. In this approach, usually periodic, input and

Armesto L. and Tornero J. (2006).

LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 67-74

DOI: 10.5220/0001209000670074

 SciTePress

output sampling hold mechanisms are represented by

two periodic and diagonal matrices. In (Tornero and

Armesto, 2003), it is demonstrated that the approach

is equivalent to many other well-known multi-rate

modeling techniques.

In this paper, we focus on multi-rate linear

quadratic Gaussian regulators, which has been pre-

viously treated in (Colaneri and de Nicolao, 1995;

Tornero et al., 1999). In (Lee and Tomizuka, 2003),

a Kalman ﬁlter is developed using the lifting tech-

nique. Shah et. al. (Shah et al., 1995) implemented a

multi-rate formulation of the iterated EKF on a biore-

actor. Kalman ﬁlters have also been used in multi-

rate digital signal processing and ﬁlter banks (analy-

sis/synthesis) (Hong, 1994). In (Zhang et al., 2004) a

Kalman ﬁlter is obtained based on It

o-Volterra equa-

tions for continuous, multi-rate and randomly sam-

pled measurements.

Techniques applied for multi-rate Kalman ﬁlter

have been also extended to non-linear multi-rate ﬁlter-

ing such as the Extended and Unscented Kalman ﬁl-

ters (Julier et al., 2000; Julier and Uhlmann, 2002). In

this sense, different multi-rate sensor fusion applica-

tions in mobile robotics have been already presented

(Armesto et al., 2004; Armesto and Tornero, 2004).

In the paper, two different but equivalent multi-

rate LQG regulators are presented, based on perio-

dic (time-variant) and on lifting techniques (time-

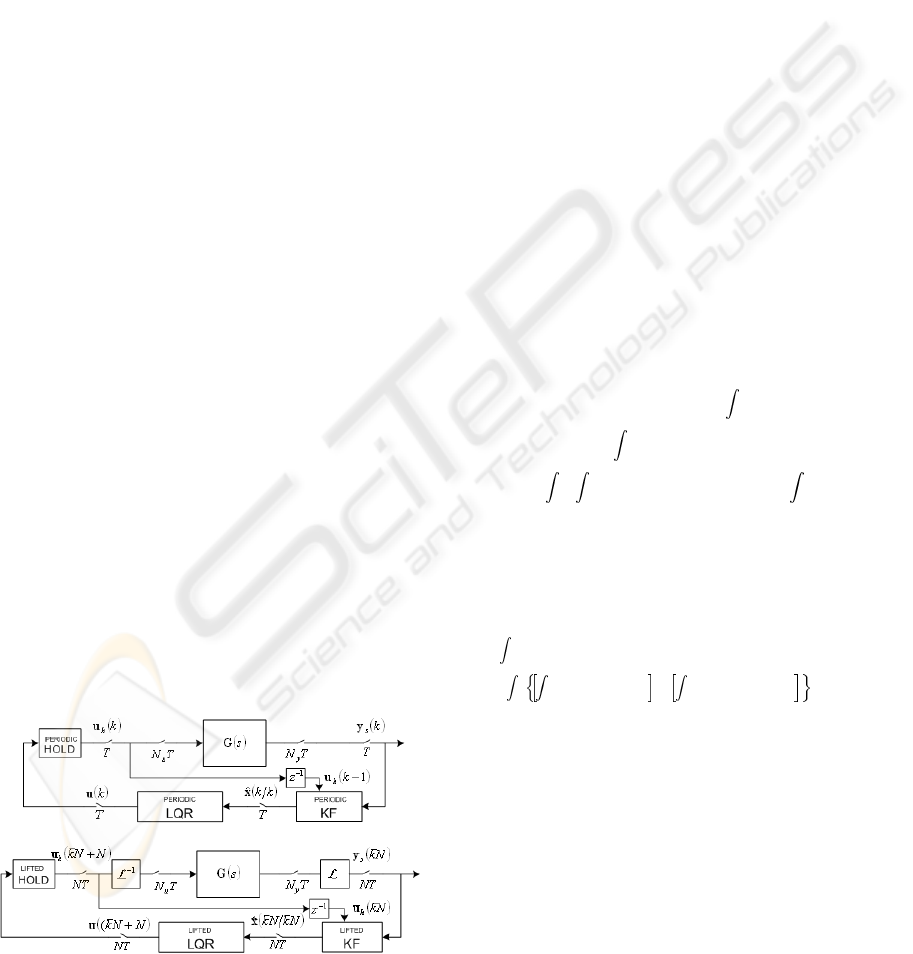
invariant), which can be summarized in ﬁgure 1. One

of the most important contributions comes from the

fact that multi-rate holds are integrated into LQG reg-

ulators. Another contribution is the demonstration

of convergence of discrete-time Kalman ﬁlter to the

continuous one (Bucy-Kalman), when the periodic-

ity ratio goes to inﬁnity. In addition, multi-rate holds

are deﬁned according to general primitive functions,

which can generate conventional ZOH and FOH as

well as others holds based on Bezier, exponential or

sinusoidal functions (Armesto and Tornero, 2003).

Figure 1: Multi-rate LQG control structures.

2 MULTI-RATE TIME-VARIANT

PERIODIC LINEAR

QUADRATIC GAUSSIAN

REGULATOR

2.1 Sampled-data System Model

Suppose a continuous-time stochastic system:

˙x(t)=A

·x(t)+B

·u(t)+G

·w(t)

y(t) =C·x(t)+v(t)

where A

∈ ℜ

n×n

is the state matrix, B

∈ ℜ

n×m

in-

put matrix and C ∈ ℜ

p×n

output matrix, being n, m

and p the dimensions of the state x(t), input u(t) and

output y(t), respectively; G

∈ ℜ

n×g

is the system

noise transmission matrix, coupling the system noises

with the state; w (t) ∈ ℜ

g×1

and v(t) ∈ ℜ

p×1

are inde-

pendent Gaussian Wiener processes with covariances

∈ ℜ

g×g

and R

∈ ℜ

p×p

, respectively.

The sampled-data system with discrete inputs at

base period is (Loan, 1978):

x((k+1)T )=A(T)·x(kT )+B(T )·u(kT )+w(kT )

(1)

y(kT )=C·x(kT )+v(kT ) (2)

with,

A =A(T ) =e

B =B(T ) =

(T−τ )

dτ

w(kT ) =

(T−τ )

w(τ −kT )dτ

v(kT ) =C

(T−τ )

dw(τ −k T )dt+

dv(τ −kT )

In the remainder of the paper, we use notation x(k)=

x(kT ), u(k) = u(kT ), y(k) = y(kT ), w(k) =

w(kT ) and v(k) = v(kT ), with discrete covariances

Q=Q(T ) and R =R(T ) computed as (Colaneri and

de Nicolao, 1995),

Q =

(T−τ )

·G

·Q

·G

·e

(T−τ )

dτ

R =C

(s−τ)

dτ C

2.2 Multi-rate Time-Variant

Periodic High Order Holds

Multi-rate high-order holds (MR-HOH) are used

as multi-rate interfaces between signals at differ-

ent sampling frequencies (Tornero and Tomizuka,

2002). Low-frequency signals are extrapolated to

high frequency, usually at base-period. In (Armesto

and Tornero, 2003), it was proposed a methodol-

ogy for designing MR-HOHs based on primitive

functions such as polynomial extrapolation, approx-

imation functions (Bezier) and even non-polynomial

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

Table 1: Multi-rate High Order Holds Based on Polynomial

Extrapolation Functions.

Name Order Primitive function u

(t)

ZOH 0 u(t

)

FOH 1 1+

t−t

−t

j−1

·u(t

)−

t−t

−t

j−1

·u(t

j−1

)

NOH n

l=0

q=0

q6=l

t − t

j−q

j−l

− t

j−q

· u(t

j−l

)

Table 2: Multi-rate High Order Holds Based on Polynomial

Extrapolation Discrete Functions.

Name Order Primitive function u

(t)

ZOH 0 u(jN

T )

FOH 1 1+

·u(jN

T )−

·u((j −1)N

T )

NOH n

l=0

q=0

q6=l

i + qN

(q − l)N

· u((j − l)N

T )

functions (exponential, sinusoidal, etc). In (Kabamba,

1987), other Generalized Sampled-data Hold Func-

tions (GSHF) can be found.

Multi-rate sampled-data systems are obtained com-

bining different MR-HOH and the continuous-time,

providing different system performance (Braslavsky

et al., 1998).

In Table 1 it can be found the primitive functions

for polynomial extrapolation functions used to gener-

ate conventional ZOH, FOH and even the general case

NOH (N-th Order Hold).

Primitive functions use signal samples at low fre-

quency as control point for generating an extrapolated

continuous-time signal,

(t) =

l=0

n,l

(t, t

, t

j−1

, . . . , t

j−l

)·u(t

j−l

) =

l=0

n,l

(·)u(t

j−l

)

where n is the order of the hold device and t

is the

time of the last updated input, with t

≤ t < t

j+1

The discrete function expressed at base-period with

regular sampling is,

(k ) =

l=0

∗

n,l

(i, N

) · u((j−l)N

T )

where t

= j · N

· T , t

− t

j−1

= N

and i =

Mod(k, N

) = k − jN

. Table 2 shows the signal

sampled at high frequency for ZOH, FOH and NOH.

In order to describe the multi-rate input sampling

at base-period, a periodic diagonal matrix is deﬁned

(Tornero, 1985),

∆

(k ) = diag{δ

(k ), v = 1, 2, . . . , m}

(k ) =

1 if Mod(k, N

)= 0

0 otherwise

According to this, the periodic representation for

multi-rate high-order holds (Armesto and Tornero,

2003) is ,

(k+1) = A

(k )·υ

(k )+B

(k )·u(k) (3)

(k ) = C

(k )·υ

(k )+D

(k )·u(k) (4)

where υ

(k) is an auxiliary state vector related to the

input hold mechanism. The periodic multi-rate hold

matrices are deﬁned as,

(k) =

I−∆

(k) 0 . . . 0

∆

(k) I−∆

(k) . . . 0

0 . . . ∆

(k) I− ∆

(k)

(k) =

∆

(k)

(k) =

∗

n,0

(·) f

∗

n,1

(·) . . . f

∗

n,n

(·)

• [I−∆

(k)]D

(k) = ∆

(k)

Despite of the mathematical complexity, the perio-

dic state-space representation for a MR-ZOH is sim-

ply,

(k+1) = (I−∆

(k ))·υ

(k )+∆

(k )·u(k)

(k ) = (I−∆

(k ))·υ

(k )+∆

(k )·u(k)

which means that the input u(k) is incorporated into

the state on every update (at low frequency) and the

output u

(k) maintains this value until the next up-

date. For a MR-FOH the formulation is,

(k+ 1)

(k− N

+1)

I−∆

(k) 0

∆

(k) I−∆

(k)

(k− N

)

∆

(k)

u(k)

(k)=

−

• [I−∆

(k)]

(k)

(k− N

)

+∆

(k)u(k)

where • represents the inner product. In this case,

the present updated input and the last updated input

are stored in the state and used to generate a ramp

based on these values at the output. In section 3.1

it is shown a very simple numerical example of the

transfer function of several holds.

2.3 Multi-rate Time-Variant

Periodic Stochastic System

A general multi-rate periodic stochastic system can

be seen as the concatenation of a multi-rate high or-

der hold (3) and (4) and the discrete-time stochastic

model (1) and (2) at base-period. Note that, we have

expressed the multi-rate stochastic system in terms of

k instead of k + 1 because the LQG requires the es-

timation of x(k) in real-time, that is at the present

sampling period k,

x(k ) = A·x(k−1)+B·u

(k−1)+w(k−1) (5)

(k ) = C

(k )·x(k)+ v

(k ) (6)

where y

(k) only contains measured outputs, C

(k)

is the row-reduced matrix of C and v

(k) is the re-

duced noise vector, respectively. In the remainder of

the paper, matrices and vectors affected by the multi-

rate sampling will be also denoted with sub-index s.

The size-varying output vector is deﬁned as,

(k ) ⊂ y

(k )∈ ℜ

p(k)×1

if δ

(k ) = 1

(k ) =

1 if Mod(k, N

)= 0

0 otherwise

being p(k) the number of sampled outputs at a given

time instant k. In fact, the complete state-space repre-

sentation of the multi-rate system including the hold

is,

(k) = A

(k−1)x

(k−1)+B

(k−1)u(k−1)+

w(k−1)

(k) = C

(k)·x

(k)+ v

(k)

LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS

where x

(k) = [x(k) υ

(k)]

and,

(k) =

A BC

(k)

0 A

(k)

(k) =

(k)

(k) = [C

(k) 0]

2.4 Multi-rate Time-Variant

Periodic Kalman Filter

According to the periodic multi-rate stochastic system

(5) and (6), we deﬁne the periodic estimation model,

ˆx(k|k −1) = A·ˆx(k−1|k −1)+B·u

(k−1)

ˆx(k|k) = ˆx(k|k−1)+K

(k)·(y

(k)−C

(k)·ˆx(k|k−1))

Note that the state of the hold is not included, since

it is completely known. Therefore, input of the esti-

mation model is the output of the hold. In this sense,

equations related with the Kalman Gain K

(k) and

output covariance matrix S

(k) are affected by the

multi-rate output sampling, while the equation related

with the state covariance prediction P(k|k−1) is not

affected. Therefore, the multi-rate periodic Kalman

ﬁlter (MR-PKF) equations are,

P(k |k−1) =A·P(k−1|k−1)·A

(k ) = P(k|k−1)·C

(k )·S

−1

(k )

(k ) = C

(k )·P(k|k−1)·C

(k )+R

(k )

P(k |k)= P(k|k−1) − K

(k )·C

(k )·P(k|k−1)

Special attention requires the case p(k) = 0, where

outputs are not sampled. The output vector is void and

also each vector/matrix denoted with sub-index s. It

is not possible to correct the state and its covariance,

and they both are simply predicted.

2.5 Multi-rate Time-Variant

Periodic Linear Quadratic

Regulator

Suppose a single-rate index as follows,

∞

k=0

(k ) u

(k )

x(k )

u(k)

(7)

with

M and

R weighting matrices for states

and inputs previously computed from a discrete-time

continuous-time index,

∞

(t) u

(t)

0 R

x(t)

u(t)

dt (8)

with,

Q =

M =

dτ

R =

dτ

dt+

·T

The multi-rate periodic equivalent index to the

single-rate one considering the hold is,

∞

k=0

(k) u

(k)]

x(k)

(k)

∞

k=0

(k) u(k)]

(k) M

(k)

(k) R

(k)

u(k)

where,

(k) =

(k)

M C

(k)

(k) =

(k)

(k) = D

(k)

The optimal multi-rate control input is obtained

from the solution of the N-Periodic Riccati equation

(Tornero et al., 1999),

(k ) = A

(k )−B

(k )·R

−1

(k )·M

(k )

(k ) =

(k )·S

(k+1)·[

(k )+K

(k ))]+

(k )−M

(k )·R

−1

(k )·M

(k )

(k ) = [R

(k )+B

(k )·S

(k+1)·B

(k )]

−1

· B

(k )·S

(k+1)·

(k )

u(k)= −(R

−1

(k )·M

(k )+K

(k ))·x(k)

Remark 1 R

(k) is singular if non one input is up-

dated. This apparent problem can be solved since el-

ements related with non updated inputs do not affect

to the index (Colaneri and de Nicolao, 1995).

3 MULTI-RATE LIFTED LINEAR

QUADRATIC GAUSSIAN

REGULATOR

3.1 Multi-rate Lifted High Order

Holds

The lifting technique for the dual-rate HOH gives the

lifted transfer function expressed at frame-period,

(¯z) =[I

l=0

∗

n,l

(1) · ¯z

−l

. . .

l=0

∗

n,l

(N − 1) · ¯z

−l

]

where inputs are updated once per frame-period. This

transfer function is derived from the state-space rep-

resentation is as follows,

¯υ

(

kN +N)=

·¯υ

(

kN)+

·¯u(

kN)

¯u

(

kN) =

·¯υ

(

kN)+

·¯u(

kN)

where,

(¯z) =

¯zI −

−1

0 0 . . . 0

I 0 . . . 0

0 . . . I 0

0 . . . 0 0

∗

n,1

(1) . . . f

∗

n,n

(1) 0

∗

n,1

(N −1) . . . f

∗

n,n

(N −1) 0

∗

n,0

(1)

∗

n,0

(N −1)

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

Table 3: Numerical Examples of Lifted Transfer Function

of MR-HOHs.

N DR-ZOH DR-FOH DR-SOH

1 G

= 1 G

= 1

2 G

3¯z−1

2¯z

15¯z

−10¯z+3

8¯z

3 G

4¯z−1

3¯z

5¯z−2

3¯z

14¯z

−7¯z+2

9¯z

20¯z

−16¯z+5

9¯z

Lifted MR-HOH for a periodic sampling can be ob-

tained using successive substitution of equation (3)

and (4). In that case, the lifted input vector is ¯u(

kN)=

(

kN−N) . . . u

(

kN−2N

) u

(

kN−N

)]

. In

order to show that despite of the mathematical com-

plexity the implementation of MR-HOH is very sim-

ple, since at the end they are composed with simple

transfer functions. In this sense, table 3 shows the

lifted transfer functions of ZOH, FOH and SOH.

3.2 Multi-rate Lifted Stochastic

System

A general multi-rate lifted stochastic system is ob-

tained by combining multi-rate holds with the sto-

chastic system,

¯x(

kN ) =

A· ¯x((

k−1)N)+

B· ¯u

(

kN )+

G· ¯w(

kN )

¯y

(

kN ) =

·¯x((

k−1)N)+

·¯u

(

kN )+

· ¯w(

kN )+¯v

(

kN )

with lifted signals,

¯w(

kN) =[w

(

kN −N) . . . w

(

kN −2) w

(

kN −1)]

¯y

(

kN) = [y

(

kN −N +N

) . . . y

(

kN −N

) y

(

kN)]

¯v

(

kN) = [v

(

kN −N +N

) . . . v

(

kN −N

) v

(

kN)]

and,

A = A

B =

N−1

·B A

N−2

·B . . . B

G =

N−1

N−2

. . . I

C·A

C·B 0 . . . 0

C·A

·B C·B . . . 0

C·A

N−N

·B C·A

N−2N

·B . . . C·B

C 0 . . . 0

C·A

C . . . 0

C·A

N−N

C·A

N−2N

. . . C

In fact, the complete state-space representation, in-

cluding the hold, is:

¯x

(

kN ) =

¯x

((

k−1)N )+

¯u(

kN )+

G ¯w(

kN )

¯y

(

kN ) =

¯x

((

k−1)N )+

¯u(

kN )+

¯w(

kN )+¯v

(

kN )

where ¯x

(

kN) = [¯x(

kN) ¯υ

(

kN)]

and,

B·

3.3 Multi-rate Lifted Kalman Filter

(MR-LKF)

The lifted estimation model is,

¯x(

kN |(

k−1)N )=

A·

¯x((

k−1)N |(

k−1)N )+

B·¯u

(

kN )

¯x(

kN |

kN ) =

¯x(

kN |(

k−1)N )+

(

kN )·(¯y

(

kN )−

¯x((

k−1)N |(

k−1)N )−

·¯u(

kN ))

where

(

kN) is the Kalman correction matrix. Once

again, the state of the hold is not estimated since it is

assumed to be completely known.

Kalman ﬁlter equations for the lifted model are,

kN |(

k−1)N) =

A·

P((

k−1)N|(

k−1)N)·

G·

Q·

xy,s

(

kN |(

k−1)N) =

P((

k−1)N|(

k−1)N)

yy,s

(

kN ) =

P((

k−1|)N|(

k−1|)N)

(

kN ) =

xy,s

(

kN |(

k−1)N)·

−1

yy,s

(

kN ) (9)

kN |

kN ) =

kN |(

k−1)N)−

(

kN )·

xy,s

(

kN |(

k−1)

where the enlarged covariance matrices are,

Q = E[ ¯w(

kN)· ¯w

(

kN)]

=E[¯v

(

kN)·¯v

(

kN)]

3.4 Multi-rate Lifted Linear

Quadratic Regulator

The multi-rate lifted equivalent index to the single-

rate one (8) considering the hold is,

∞

k=0

[¯x

(

kN ) ¯u

(

kN )]·

¯x

(

kN )

¯u(

kN )

where,

A 0 0

with,

Q=diag{

Q, . . . ,

M=diag{

M, . . . ,

R=diag{

R, . . . ,

A =

B =

0 . . . 0 0

B . . . 0 0

N−1

B . . . B 0

The optimal control input is obtained from the so-

lution of the Riccati equation in a similar way,

(

kN ) =

−

−1

−

−1

]

(

kN +N)·[

−

(

−1

(

kN ))]

(

kN ) = [

(

kN +N)

]

−1

(

kN +N)·

·(

−

−1

)

¯u(

kN +N) = −(

−1

(

kN ))·¯x(

kN )

LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS

4 MULTI-RATE BUCY-KALMAN

FILTER

The limit case, when N → ∞ with constant frame-

period, both discrete-time Kalman ﬁlters converge to

their equivalent continuous-ones. Continuous lifting

technique must be applied to converge MR-LKF into

its equivalent one (Bamieh et al., 1991). In this pa-

per the convergence of MR-PKF to the Bucy-Kalman

ﬁlter (continuous) is shown.

The prediction and correction covariance equations

for a sampled-data system is,

P(t+T |t)= e

·P(t|t)·e

+ Q(T )

(t)= C

(t)P(t+T |t)C

(t)+R

(T )

(t+T )= P(t+T |t)·C

(t)·S

−1

(t)

P(t+T |t+T )= P(t+T |t)−K

(t+T )·C

(t)·P(t + T |t)

being C

(t) the output matrix considering the multi-

rate sampling. The derivate of the covariance is,

P(t|t) = lim

T →0

P(t+T |t+T )−P(t|t)

P(t|t) = lim

T →0

∂P(t+T |t)

∂T

− lim

T →0

∂K

(t+T )

∂T

·C

(t)·P(t+T |t)−

− lim

T →0

(t+T )·C

(t)·

∂P(t+T |t)

∂T

Operating and re-ordering some terms,

lim

T→0

∂P(t+T |t)

∂T

P(t|t) = A

·P(t|t)+P(t|t)·A

·Q

·G

lim

T→0

∂K

(t+T )

∂T

(t)P(t+T |t) =

P(t|t)C

(t)K

(t)−

−K

(t)

(t)K

(t)

lim

T→0

(t+T )C

(t)

∂P(t+T |t)

∂T

= K

(t)C

(t)

P(t|t)

where

−1

(t) = −S

−1

(t)

(t)S

−1

(t). Operating, we

get to multi-rate Bucy-Kalman ﬁlter equations:

P(t|t)= A

·P(t|t)+P(t|t)·A

·Q

·G

(t)=

P(t|t)C

(t)

P(t|t)C

(t) + R

(t)

−1

P(t|t)=

P(t|t)−K

(t)·C

(t)·P(t|t)

Finally, the state estimation is as follows:

˙x(t)= A

·ˆx(t)+B

·u

(t)+K

(t)(y

(t)−C

(t)·ˆx(t))

5 NUMERICAL EXAMPLE

Suppose the weak-coupled plant proposed by (Araki

and Yamamoto, 1986; Godbout et al., 1990), with in-

puts u

and u

updated at T

= 0.1sec. and T

0.15 sec. and outputs y

and y

sampled at T

= 0.15

sec. and T

= 0.1 sec., respectively. The base-period

is T = 0.05 sec. and the frame-period

T = 0.3 sec.,

thus N =6.

˙x(t)= A

·x(t)+B

·u(t)+w(t)

y(t) =C·x(t)+v(t)

with,

x(t)= [x

]

, u(t)= [u

]

, y(t) = [y

]

=diag{−2.5, −2, −1}

2.5 0

10 −1.2

5/6 1

, C =

−4 1 0

−1/3 0 1

where noise covariances are Q

diag{0.05, 0.3, 0.1} and R

=diag{0.1, 0.1}.

The lifted input and output vectors are:

¯u(

kN ) = [u

(

kN−N ) u

(

kN−N ) u

(

kN−4) u

(

kN−3) u

(

kN−2)]

¯y

(

kN ) = [y

(

kN−4) y

(

kN−3) y

(

kN−2) y

(

kN ) y

(

kN )]

while the periodic time-variant vectors and matrices

are,

∆

(0) = I ∆

(1) = 0 ∆

(2) = ∆

(4) =

1 0

0 0

∆

(3) =

0 0

0 1

(0) = [y

]

, y

(1) = y

(5) = ∅, y

(2) = y

(4) =y

, y

(3) = y

Figure 2 shows the state covariance computation

using a MR-LKF and MR-PKF for unit step with

ZOH. The MR-LKF is combined with the fast sam-

pling model of the plant (inter-sampling prediction).

It can be observed that the covariance (and also the

estimation error, which is not represented), are the

same at every frame-period, therefore both ﬁlters are

equivalent at those time instants. However, the advan-

tage of the multi-rate periodic time-variant approach

is that estimations are performed at a fast sampling

rate, while the lifting approach is in open-loop until

all inputs and output of the frame-period have been

processed.

0 0.5 1 1.5

0.05

0.1

+3σ x

0 0.5 1 1.5

0.1

0.2

+3σ x

0 0.5 1 1.5

0.1

0.2

Time [sec.]

+3σ x

Figure 2: State covariance for MR-LFK (dotted line) and

MR-PKF (dashed line).

Now, can compare the equivalence of the perio-

dic and lifted LQG control using a ZOH. In ﬁgure

3, it is depicted the state evolution with initial val-

ues x(0) = [0.5 −0.4 0.3]

, and weighting matrices

= 10·I

3×3

= 0.1·I

2×2

. It can be appreciated

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

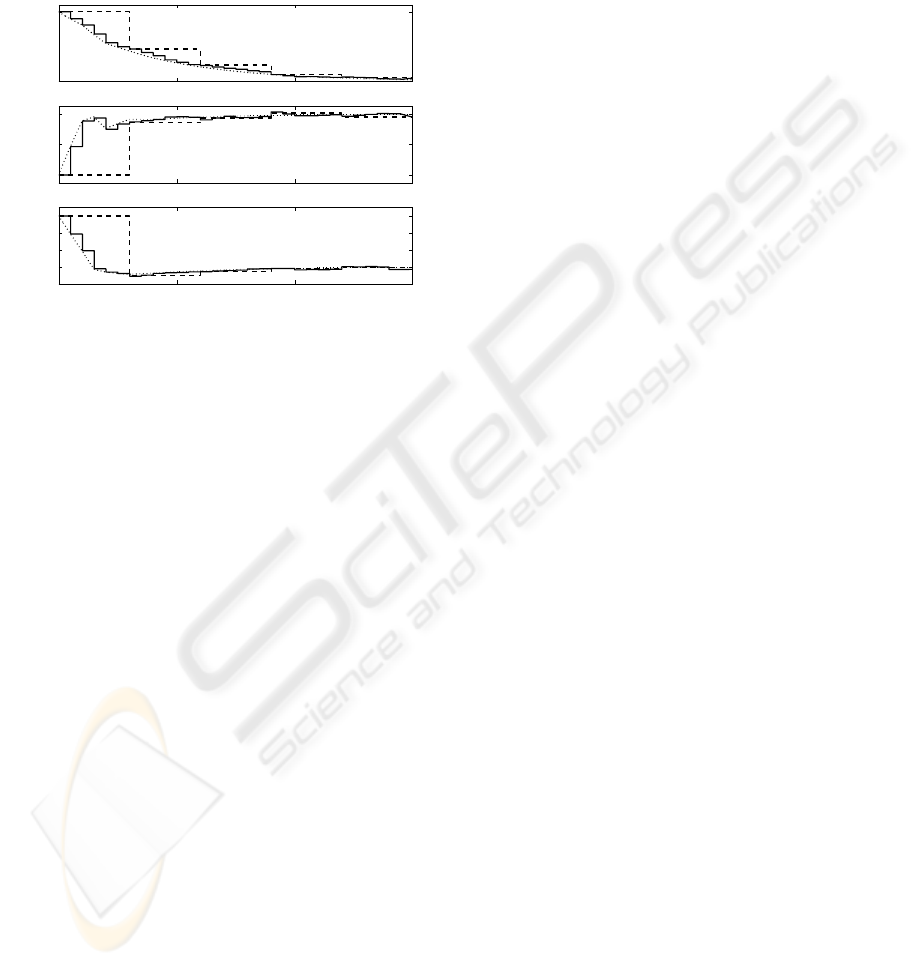
that in both cases, they give the same estimation each

frame-period, however in the periodic approach the

state estimation is much more closer to the real state.

This is because the lifted LQG is in open-loop among

frame-periods. Figure 3 shows the state evolution for

the proposed example, where the same conclusions

can be obtained.

0 0.5 1 1.5

0.5

0 0.5 1 1.5

−0.4

−0.2

0 0.5 1 1.5

−0.1

0.1

0.2

0.3

Time [sec.]

Figure 3: State estimation in LQG control, with the perio-

dic regulator (solid line) with the lifted regulator (dashed

line) and the real state evolution of multi-rate LQR control

(dotted-line).

6 CONCLUSIONS

In this paper, we have presented and formalized two

Linear Quadratic Gaussian regulators for multi-rate

sampled-data systems, using time invariant (lifting

technique) and time variant (periodic) modeling. In

the numerical example, it has been shown that both

approaches are equivalent at frame period, since they

are representing the same sample-data system.

The lifted LQG regulator is expressed with con-

stant coefﬁcient matrices and executed at the frame-

period. This implies a partial open loop control

among frame-periods. On the contrary, the periodic

LQG is executed at base-period and consequently, it

is a time-variant system. In addition, this regulator

is not restricted to periodic sampling and can also be

used for dealing with data-missing problems without

recomputing the system model.

In both regulators, multi-rate holds are integrated

as signal interfaces for different frequencies. Gen-

eral multi-rate holds are based on primitive functions.

In particular, from polynomial functions it is possible

to generate multi-rate ZOH, FOH, etc. Other less-

conventional holds based on non-polynomial func-

tions may improve signal reconstruction and even sys-

tem behavior. The wide variety of holds proposed di-

rectly in this paper or indirectly in other authors’ ref-

erences, open a research ﬁeld to be exploited.

An interesting analysis has been done to demon-

strate the convergence of the Periodic Kalman ﬁlter

to its equivalent continuous one (Bucy Kalman ﬁl-

ter), when the periodicity ratio converges to inﬁnity.

A new approach related with Bucy Kalman ﬁlter is

the fact that continuous signals with discontinuities

can be easily incorporated for estimation.

The multi-rate periodic modeling can be also used

in non-linear ﬁlters such as Extended and Unscented

Kalman Filters and Particle Filters, widely used in

mobile robotics.

Many technological limitations associated to sen-

sors and actuators can be overtaken in a systematic

way, using the multi-rate sampling approaches used

in this paper.

REFERENCES

Albertos, P. (1990). Block Multirate Input-Output model

for sampled-data control systems. IEEE Trans. on Au-

tomatic Control, AC-35(9):1085–1088.

Araki, M. and Yamamoto, K. (1986). Multivariable mul-

tirate sampled-data systems: State-space description,

transfer characteristics and nyquist criterion. IEEE

Trans. on Automatic Control, AC-31(2):145–154.

Armesto, L., Chroust, S., Vincze, M., and Tornero, J.

(2004). Multi-rate fusion with vision and inertial sen-

sors. In Int. Conf. on Robotics and Automation, pages

193–199.

Armesto, L. and Tornero, J. (2003). Dual-rate high order

holds based on primitive functions. In American Con-

trol Conference, pages 1140–1145.

Armesto, L. and Tornero, J. (2004). Slam based on kalman

ﬁlter for multi-rate fusion of laser and encoder mea-

surements. In IEEE Int. Conf. on Intelligent Robots

and Systems, pages 1860–1865.

Bamieh, B., Pearson, J., B.A., F., and A., T. (1991). A lift-

ing technique for linear periodic systems with appli-

cations to sampled-data control. Systems and Control

Letters, 17:79–88.

Braslavsky, J. H., Middleton, R. H., and Freudenberg, J. S.

(1998). L2-induced norms and frequency gains of

sampled-data sensitivity operators. IEEE Trans. on

Automatic Control, 43(2):252–258.

Chen, T. and Francis, B. (1995). Optimal Sampled-data

Control Systems. Springer-Verlag, London.

Colaneri, P. and de Nicolao, G. (1995). Multirate LQG con-

trol of continuous-time stochastic systems. Automat-

ica, 31:591–596.

Godbout, L., Jordan, D., andApostolakis, I. (1990). Closed-

loop model for general multirate digital control sys-

tems. In IEEE Proceedings, volume 137 of D, pages

326–336.

LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS

Hong, L. (1994). Multirate estimation. In Proceedings

of the IEEE Aerospace and Electronics Conferences,

pages 435–440.

Julier, S. and Uhlmann, J. (2002). Reduced sigma points

ﬁlters for the propagation of means and covariances

through nonlinear transformations. In American Con-

trol Conference, volume 2, pages 887–892.

Julier, S., Uhlmann, J., and Durrant-Whyte, H. F. (2000).

A new method for the nonlinear transformations of

means and covariances in ﬁlters and estimators. IEEE

Transactions on Automatic Control, AC-45:477–482.

Kabamba, P. (1987). Control of linear systems using gen-

eralized sampled-data hold functions. IEEE Transac-

tions on Automatic Control, pages 772–783.

Khargonekar, P., Poolla, K., and Tannenbaum, A. (1985).

Robust control of linear time-invariant plants using

periodic compensation. IEEE Transactions on Auto-

matic Control, AC-30:1088–1985.

Kranc, G. (1957). Input-output analysis of multirate feed-

back systems. IEEE Transactions on Automatic Con-

trol, AC-3:21–28.

Lee, D. and Tomizuka, M. (2003). Multirate optimal state

estimation with sensor fusion. In American Control

Conference, pages 2887–2892.

Loan, C. V. (1978). Computing integrals involving the

matrix exponential. IEEE Trans. Automatic Control,

23:395–404.

Qui, L. and Chen, T. (1999). Multi-rate sampled-data sys-

tems: All H

∞

suboptimal controllers and the mini-

mum entropy controller. IEEE Trans. Automatic Con-

trol, 44(3):537–550.

Shah, S., Gudi, R., and M.R., G. (1995). Adaptative multi-

rate state and parameter estimation strategies with ap-

plication to a bioreactor. AICHE Journal, 412:2451–

2464.

Tangirala, A., Li, D., Patwardhan, R., Shah, S., and Chen,

T. (1999). Issues in multi-rate process control. In Pro-

ceedings of the American Control Conference, pages

2771–2775.

Tornero, J. (1985). Non-conventional sampled-data systems

modelling. Control System Center Report 640/1985,

University of Manchester (UMIST).

Tornero, J., Albertos P., and Salt J. (1999). Periodic optimal

control of multirate sampled data systems. In 14th

World Congress of IFAC, pages 211–216, China.

Tornero, J. and Armesto, L. (2003). A general formulation

for generating multi-rate models. In American Control

Conference, pages 1146–1151.

Tornero, J. and Tomizuka, M. (2002). Modeling, analysis

and design tools for dual-rate systems. In American

Control Conference, pages 4116–4121.

Zhang, H., Basin, M., and Skliar, M. (2004). Optimal

state estimation with continous, multirate and ran-

domly sampled measurements. In Proceedings of the

American Control Conference.

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL