
HEAT-AND-POWER PROCESSES OPTIMIZATION BY MEANS
OF MODEL-BASED SIMULATION
Dmitry Antropov
JSC, Etalon MCS“, Kazan, Russia
Rosica Ivanova, Renat Sadykov
Kazan State Architectural Building University, Kazan, Russia
Sergey Yeryomin, Rauf Kafiatullin
PO “Kazenergo“, Kazan, Russia
Keywords: Intelligent systems in education, system integration, intelligent laboratory-scale plant.
Abstract: A firmware was developed for simulation of heat-mass transfer processes in power equipment such as steam
or water boilers and dryers. Hardware of this pilot plant is based on modern microprocessors control
devices. Software rests on specially developed mathematical models. The functions and structure of the
model of fully automated boiler and dryer control system (B-DCS) are described in detail. One of the
variants of implementation of B-DCS on the example of the dryer unit for drying bioactive products is
considered. The analysis of the optimality criterion problem and selection of the optimal control structure
are reviewed using Pontryagin’s maximum principle. The objective of optimization is to reduce
expenditures of operational process.
1 INTRODUCTION
The depletion of the resources of extensive
development of economy makes critical the issues of
the development of intensive process technologies
and their introduction in the industry. In the rapidly
developing technologies these challenges can be
competitively met only by methods of computerized
mathematical modelling which reduces the amount
and time of R&D required and enhances its quality.
The realization of these advantages in the
computerized automated design and control systems,
scientific research requires the unity of
mathematical, algorithmic, informational and
software support for various processes and tasks in
power engineering, chemical technology and
biotechnology. This unity should be based on the
generalizing mathematical models (MM) covering
the basic aspects of the development of the intensive
process technologies. However, in common practice
highly specialized MMs of empirical character
down to regressive ones are in use owing to the fact
that the conventional, more universal MMs do not
adequately incorporate such features of the
intensive process tecnologies as multi component
structure and lability of the process agents, low
process observability and reproducibility, intensity
and coherency of various features of the happening
phenomena, interference of process technology
stages.
We have designed a model of a fully automated
boiler and dryer control system (B-DCS) based on
the microprocessor data acquisition and control
devices designated for training of the students.
The B-DCS model allows to familiarize with the
processes taking place in the boiler and drying units
in the absence of processing system. It allows to
solve problems of mathematical modelling adequacy
of the basic processes in a boiler or a dryer. The
capacity of the B-DCS processing unit permits to
realize complicated optimization algorithms and to
analyze their efficiency.
207
Antropov D., Ivanova R., Sadykov R., Yeryomin S. and Kafiatullin R. (2006).
HEAT-AND-POWER PROCESSES OPTIMIZATION BY MEANS OF MODEL-BASED SIMULATION.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 207-212
DOI: 10.5220/0001210602070212
Copyright
c
SciTePress

2 FUNCTIONS OF THE B-DCS
The intelligent laboratory-scale plant implements the
following functions of the automatic control and
supervision:
Boiler automated control:
− Boiler control in an automatic mode using the set
algorithm (check readiness for start-up,
ventilation, kindling, initial heating, output of
operating conditions, shut down;
− Boiler regulation using basic process parameters
(load, fuel - air ratio, chamber pressure, etc.);
− Implementation of the process protection and
interlocking;
− Diagnosis of the boiler process equipment
condition;
Automated control of the boiler-house auxiliaries
consists of:
− Control of the deaeration unit, network, and
intake pumps;
− Water level control in the additional feed tank;
− Regulation of the temperature schedule and
heating system hydraulic mode;
− Energy transmitter logs (gas, steam, heat) and
automatic regulation of thermal energy output for
customers.
Dryer automated control and remote supervision:
Includes the following process control objects:
dryer; charging device; unloading mechanism;
receiver; condenser; hotwell.
Controlled parameters:
− dryer top pressure; pressures upstream of a
receiver.
− dryer lower part temperature; inlet and outlet air
temperatures;
− inlet and outlet product temperatures ;
− air consumption in a dryer;
3 STRUCTURE OF THE B-DCS
The B-DCS model includes the following basic
levels (fig. 1):
− emulation of sensing transducers and actuators
level
− processing unit level
− human interface (HI) level.
Field level - the level of the sensing transducers
and actuators. In the laboratory-scale plant the role
of sensing transducers is played by PC with program
emulation of a real object. Input-output (I/O)
modules are set on PC. The program simulates
functioning of field sensing transducers, emulating
their current output signals. Emulation programs
software can be based on the SCADA-system with
the proper scripts which are carrying out process
imitation or on special software based on the virtual
devices technology. Current signals are transferred
to the next level - on an input of the control unit.
4 MATHEMATICAL
MODELLING AND
OPTIMIZATION OF THE
BIOPRODUCTS DRYING
PROCESS
Let’s consider one of the variants of implementation
Figure 1: Structure of the B-DCS.
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
208
of the above mentioned B-DCS on the example of
the model of the dryer unit for drying bioactive
products. The creation and application of
computerized generalizing MMs and the
development of intensive drying process for
bioactive products exemplified by highly purified α
- amino acids.
The desiccation of highly purified α- forms of
irreplaceable amino acids as follows: Thr
(threonin), Trp (tryptophan), Leu (.Leucin), Ile (iso-
leucin) involves removal of the mixture of ethanol
(in which they are practically insoluble) and water
with solubility of 0.02-0.09 kg/kg at 20
0
C. The
residence time in vacuum dryer is up to 72 hours.
In view of the pressing requirement for the
development of commercial technology for intensive
desiccation of pure amino acids 25 types of dryers
were analyzed on the computer in an effort to find
the method of adequate intensive drying technology:
vacuum application, active hydrodynamic regimes.
A complex pilot plant was fabricated [1,2] for the
selection of appropriate drying process and the
following processes were tested : desiccation in
pseudo-liquified and densely purged beds ,
desiccation by pressure reduction (DPR), vacuum
oscillating desiccation - repeated alternation of
heating by hot gas and vacuum cooling, impulse
desiccation by depressurization of drying chamber
(DDC)- a new method proposed.
It was experimentally established that free moisture
is basically removed from the bioproducts being
investigated and they tend to agglomerate. The
agglomeration mechanism is related to the change in
the liquid phase composition upon desiccation: the
crystals partially dissolve in the mixture upon rapid
increase of water proportion (more volatile spirit is
removed faster) and subsequently start to stick to
each other. So as to loosen and break the
agglomerates the impulse depressurization was
effectively employed causing breaking normal
stresses depend-
ent on the duration and depth of terminal pressure
drop, size, inner structure and temperature of
agglomerates.
The proposed method alowed to meet the
requirements for the dispersive structure of amino
acids and to reduce
с
τ
to 0.5 hour or less. The
unit incorporates the dryer, heating agent feeding
line, depressurization system and receiver.
5 DRYING PROCESS
DESCRIPTION
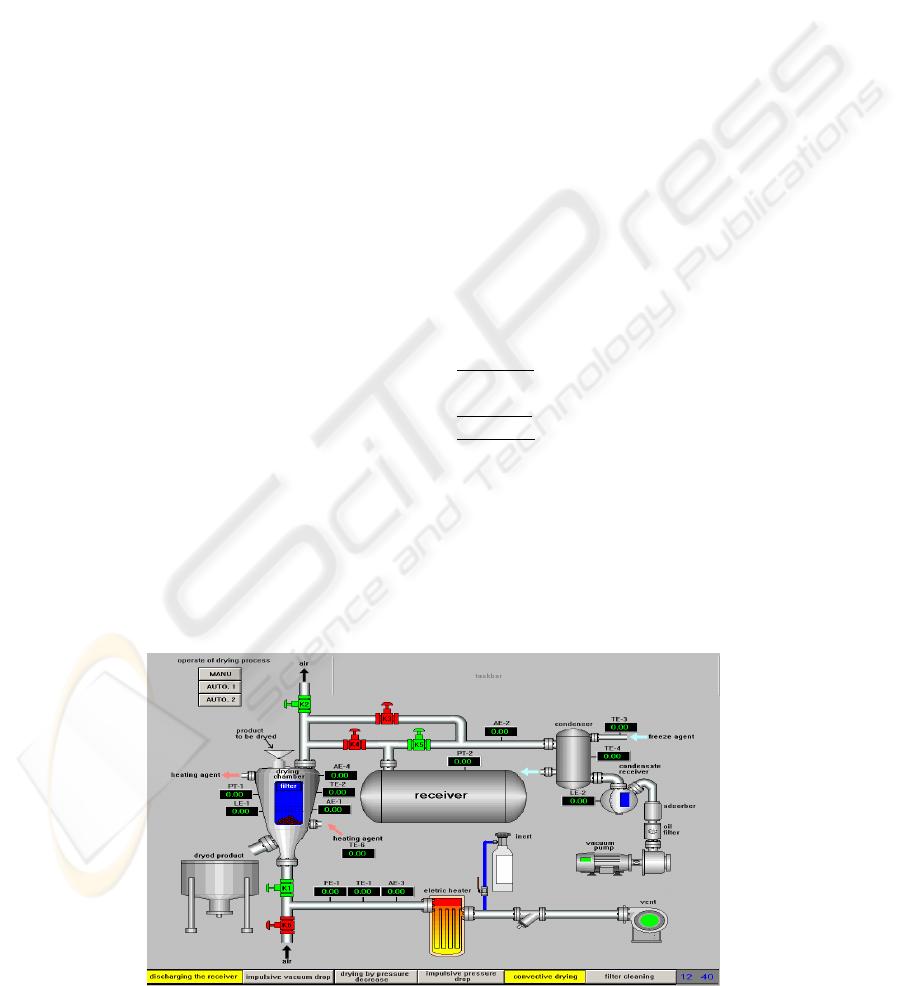
The installation scheme is represented in fig. 2
(screen shot of the engineer’s interface). The raw
material goes through the charging device of the
drying apparatus and then enters the drying
chamber. In the drying chamber the product is
exsiccated by hot air. The product is unloaded
pneumatically in the loading tank. In the drying
chamber vacuum creation is possible with the help
of pumping system consisting of the pump, the
condenser and the hotwell .The drying process can
be carried out in various ways. In emulation system
in the capacity of control and regulating blocks the
most widespread drying regimes are used.
Regime 1
– Drying in filtering and pseudo-liquefied
layers.
Regime 2
– Drying by pressure decline.
Regime 3
– Drying by the combined pressure drop
and vacuum.
This method integrates the following regimes of
drying:
− Preheating;
− Depressurization;
− Pumping out;
− Layer tossing up;
− Clearing the filter.
Figure 2: HI of the dryer unit.
HEAT-AND-POWER PROCESSES OPTIMIZATION BY MEANS OF MODEL-BASED SIMULATION
209

In the course of mathematical modelling the pressure
drop hydrodynamic calculations were made, based
on the model of stationary adiabatic flow from a
larger vessel via a confuser without friction. The
equation [2] in the explicit form was obtained for Pc.
The depressurization stage as vacuum dehydration
process was divided into two parts. The duration of
air evacuation
()
ов
τ
was calculated from the
formula [3]:
()
∫
=
κ
κ
τ
κ
τ
P
xP
ов
PPQ
dPV
00
,
)(
(1)
(1)
where V - free volume of drying chamber; k -
polytrope index; Р, Р
н
– pressures: current and
vapour saturation of multi component liquid phase;
Q (P) efficient pumping speed of vapour/air mixture
calculated by constant volume method [7];
x
G
-
vector of liquid phase composition; T - material
temperature; index "0" - adopted for initial values.
The analysis of internal heat mass transfer at the
stage of vapour pumping showed that it is described
by non linear differential equations of filtration and
heat transfer [1, 2]:
,
,
τ
ρλ
τ
ρ
τ
ρ
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
U
r
z
T
z
T
c
z
P
K
z
U
сс
pс
(2)
(2)
where
ημ
/КК
р
= - molar filtration
coefficient; К – permeability of capillar porous
solid ;
η
- kinematic viscosity coefficient of
vapour/air mixture being removed;
μ
- apparent
molecular mass of vapour/air mixture being
removed ;
с
ρ
- dry material density;
r
- heat of
vapour formation; с – specific heat;
λ
- heat
transfer coefficient; U – humidity of material;
τ
-
time; z – spatial coordinate (or material layer plane
orthogonal towards axis z ).
It was determined that heat transfer had no
influence on the process and, thus, vacuum
desiccation process has local invariants - functions
() ()
TxTU
G
,
and
()
TP which do not depend
on
τ
. The availability of invariants radically
reduces the required scope of experimental research
relating to combined heat and dehydrating influence
of desiccation process on the preparations and
facilitates kinematic calculations of desiccation
process. The measurements showed that at the layer
height H = 0.03 - 0.02 m the temperature of pressure
reduction desiccation was the same throughout the
whole product. In view of this the local invariants
play a balancing role and are calculated via
integration of the following system of ordinary
differential equations (SODE) [3]:
()
,
,
Ixy
dT
xd
UI
dT
dU
GG
G
−=
=
rUcI /
=
, (3)
whilst dehydration kinetics - by integration of
equation as follows:
[
]
()
()
[]
RTU
V
RT
R
c
r
VM
PQ
RT
q
R
cM
V
dT
dU
αμ
ρβμ
μ
ρ
τ
ρβμ
GG
G
G
G
G
G
,
,
,
⋅+
−
⋅+
+⋅−
⎟
⎠
⎞
⎜
⎝
⎛
=
, (4)
where
⋅
⋅
, - scalar product of vectors; М – mass
of dry material; R – universal gas constant; vectors
α
G
и
β
G
are determined only by the conditions of
vapour/liquid equilibrium [3],
х
G
, y
G
- vectors of
composition of liquid phase and removed vapours,
to be determined from the equation of vapour/liquid
equilibrium. The equation (4) is solved together with
the equations of material and power balance of
vapour pumping stage (DPR):
(
)
()
,
,0)(M
U,
τ
ττ
τ
ρ
ρ
τ
μ
q
d
dU
rM
d
dT
cM
d
d
VPQ
d
dU
dxyxdU
=−
=++
−
=
G
G
G
(а - liquid phase material balance) (в - vapour
material balance) (с - damp product power balance)
as ordinary differential equations system of
summarizing order n + 2.
Thus, a non trivial property of distillation material
balance was revealed (first equation of the system
(5)) to accumulate the error upon numerical
integration [3]. In system (5)
(a)
(в) (5)
(с)
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
210

ρ
- vapour density, М – dry product mass in the
dryer,
()
τ
q - heat supply rate. The system
thermodynamic parameters are determined by the
additivity rule:
хсUсс
с
GG
,+=
, (6)
yrr
GG
,=
,
where
с
с – specific heat of the dry product, c
G
and
r
G
- molar specific heat evaporation heat of the
components.
The analysis of heat mass transfer in the pseudo
liquified bed was performed within the external task
of mass exchange particle - heating agent for the
binary liquid mixture ethanol-water on the basis of
equations set (ES) of Stephan - Maxwell multi
component diffusion. The total mass exchange
intensity was set empirically by function
()
TU
в
,
ϕ
- relative air humidity at the outlet
from the layer, determined by methods of structural
risk minimization [5]. For heating stage kinetics ES
was derived:
() ()
()
()
()
,
,
,
,
,
т.н.
2
22
ττ
ττ
ϕ
ϕ
μϕμϕ
μτ
d
dU
U
xy
d
xd
TTcG
d
dU
c
r
d
dT
TxPP
TPP
TxPTP
MRT
G
d
dU
y
p
Hba
aaa
Hbaa
ya
⋅
−
=
−+⋅=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
⋅−=
GG
G
(7)
where the composition of the vapours removed
(index y) from the amino acids
у
y
G
is calculated
with consideration of water vapours heating by gas,
index 2 refers to water,
g
ρ
– gas density at normal
volume flow rate G, с
p
– gas specific heat at
constant pressure.
The stage models are included into the calculation
sequentially , are interrelated by marginal conditions
and , in the aggregate, form a common DDC
process model adequate to the experimental data
obtained [2].
The hardware and operating modes of the
bioproducts drying shop have been optimized to
reported expenses in accordance with the approaches
[6]. The task of the pressure drop system design is
delineated and solved by decomposition. The
optimum operating modes of the unit are defined by
formulation and solution of the task of optimum
control with criterion functional:
()
[]
{}
∫
−+++=
c
dETTEZGЕЕ
М
I
hiathaaipii
τ
τ
0
1
, (8)
where
i
E ($/s) – expenses irrespective of the
mode,
pi
E – cost of 1 second of vacuum pump
operation,
ai
E – cost of 1 m
3
of sterile air,
ha
E
-
cost of heating of 1 m
3
of air per 1 К, index i
designates i variant of hardware,
()
τ
Z – regime
function equal to 0 at depressurization stages and to
1 at heating stages. Allowable equations
(
)
(
)
(
)()
[
]
τ
τ
τ
τ
ψ
ZTGM
ha
,,,
=
(9)
are limited by certain conditions ensuring product
quality. The analysis of the task with the application
of maximum principle of Pontryagin revealed the
structure of optimum control:
(
)()
[
]
τ
τ
ψ
ортhaорт
ZTGM ,,,
max
maxmax
=
(10)
where
maxmax
, GM
and
max
ha
T
-
maximum allowable values of parameters. It was
revealed that the increased rate of depressurization
system results in reduction of reported expenses on
DDC bioproducts. Optimum
()
τ
орт
Z and
с
τ
highly depend on the composition of the removed
mixture (
с
τ
for spirit is 4.4 times lower than
с
τ
for water). The regime optimization reduced the
reported expenses and
с
τ
by 40 %. In comparison
with vacuum-desiccators
с
τ
is reduced by order of
1
÷
2.
6 SIMULATION RESULTS
Some tests were made with irreplaceble amino acid
– Leucin. Figure 3 shows the results of the design
data and simulation experiments for main
parameters U - liquid specific mole contention
x –
alcohol mole fraction , T – temperature of the
material.
HEAT-AND-POWER PROCESSES OPTIMIZATION BY MEANS OF MODEL-BASED SIMULATION
211

Figure 3: Design and experimental data comparison of
Leucin drying. G = 0,007 m
3
/s, T
гр
= 95 °C, Н = 0,005 m,
τ
v
= 5 min. Firm lines – design: 1 – U, 2 – x
v
, 3 – T; — —
— – T, experiment, о – U, experiment.
7 CONCLUSIONS
In this paper we have presented a task-level system
which can be used for the following purposes:
1. Students familiarization with heat-mass transfer
processes in power equipment.
2. Development and identification of new
mathematical models of above-mentioned processes.
3. Optimization of the real equipment selection and
its operation modes.
On the example of the model of the dryer unit
theoretical base for optimization of bioactive
products drying technology have been developed.
The analysis of the problem with the application of
the Pontryagin’s maximum principle has revealed
optimal control structure. At the expense of the
mode optimization the costs and time of a
α-amino
acids drying (
τ
d
) are reduced by more than 40 %. In
comparison with the vacuum-shelf dryers
τ
d
of the
bioactive products is reduced by 1 - 2 orders.
REFERENCES
Sadykov R.A., Antropov D.N. Optimum equation and
automation of desiccation technology for
bioproducts. Izvestiya RAN. Series energetics. ¹6,
2005, pp. 85-92.
Sadykov R.A., Antropov D.N. Power saving drying
technology for bioactive products. Kazan. Kazan State
Energy University, 2005, p.174.
Sadykov R.A. Transfer process at short term phase contact
(on the example of drying processes). . Kazan. Kazan
State Energy University , 2004, p.176.
Sadykov R.A., Antropov D.N., Kafiatullin R.A.
Bioproduсts drying optimal control in oscillating
regimes. ICINCO – 2005. Second international
conference on informatics in control, automation and
robotics. Barcelona, Spain, September, 14 – 17, 2005.
Vol. I. p.p. 176 – 181.
Kryanev A.V., Lukin G.V. Mathematical methods of
indefinite data processing.- M.: Phyzmatlit, 2003. 216
pp.
Baumstein I.P. Classification of the tasks of optimum
control of the drying processes.
Rozanov L.N. Vacuum technology. M.: Higher School,
1982.207 pp.
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
212
