
TRACKING MULTIPLE OBJECTS USING THE VITERBI
ALGORITHM
Andreas Kr
¨
außling, Frank E. Schneider and Stephan Sehestedt
Research Establishment for Applied Sciences (FGAN)
Neuenahrer Straße 20, 53343 Wachtberg
Keywords:
Mobile robotics, tracking, multiple targets, Viterbi algorithm, Kalman filter.
Abstract:
Tracking multiple targets is a great challenge for most tracking algorithms, since these algorithms tend to loose
some of the targets when they get close to each other. Hence, several algorithms like the MHT, the JPDAF
and the PMHT have been developed for this task. However, these algorithms are specialized on punctiform
targets, whereas in mobile robotics one has to deal with extended targets. Therefore, in this paper an algorithm
is proposed that can solve this problem. It uses the Viterbi algorithm and some geometrical characteristics of
the problem. The proposed algorithm was tested with real world data.
1 INTRODUCTION AND
RELATED WORK
For many real world applications it is essential that a
robot is able to interact with its environment. This is
true for multi–robot systems where a group of robots
has to solve a given task or where robots are supposed
to support people. For such situations, the awareness
of the position of people and other robots is a funda-
mental ability for a mobile unit to be able to interact
with its environment in an appropriate way.
This problem can be analyzed under the superordi-
nate concept of tracking. Tracking denotes the esti-
mation of the position of an object based on conse-
cutive sensor measurements. It is well studied in the
field of aerial surveillance with radar devices (Bar-
Shalom and Fortmann, 1988). In the area of mo-
bile robots tracking is also a well established research
topic (Prassler et al., 1999; Schulz et al., 2001; Fod
et al., 2002; Fuerstenberg et al., 2002). In mobile
robotics laser range scanners are one of the preferred
sensor devices. A Sick laser range scanner for ex-
ample can measure the distance to the next reflect-
ing obstacle with a high angular resolution of e.g.
0.25 degree. Lasers have rapidly gained popula-
rity for mobile robotic applications such as collision
avoidance, navigation, localization and map building
(Thrun, 1998).
The problem of tracking people and other objects in
densely populated environments with a robot–borne
laser scanner can be characterized in the following
way: most of the readings are from obstacles like
walls or other objects and only a few measurements
come from the tracked object itself. The problem
of allocation of data obtained from the presently ac-
counted target is called the data association problem
(Bar-Shalom and Fortmann, 1988). As a solution to
this problem, a tracking algorithm might use a vali-
dation gate which separates the signals belonging to
the current target from other signals. A second cha-
racteristic of tracking people with laser range scan-
ners is the occurrence of several measurements from
the same object. In contrast to common radar based
tracking sensors the Sick laser scanner has a much
higher resolution and refresh rate. This leads to the
fact that the tracked object generates several measure-
ments. Therefore, we have to deal with what we call
extended objects instead of punctiform objects like in
the common radar tracking literature. Thereby, punc-
tiform targets are those ones, which are the origin of
just one measurement. A third characteristic of track-
ing in the field of mobile robotics is the occurrence of
crossing targets. This means that two or more targets
get very close to each other, so that they cannot be
separated by common tracking algorithms (Fortmann
et al., 1983), (Kr
¨
außling et al., 2005). This situation
can appear e.g. when two humans meet, talk to each
other and split again and is a well known problem in
mobile robotics (Prassler et al., 1999).
There are several methods for tracking punctiform
18
Kräußling A., E. Schneider F. and Sehestedt S. (2006).
TRACKING MULTIPLE OBJECTS USING THE VITERBI ALGORITHM.
In Proceedings of the Third Inter national Conference on Informatics in Control, Automation and Robotics, pages 18-25
DOI: 10.5220/0001215200180025
Copyright
c
SciTePress

crossing targets in clutter:
1. the MHT (Multi Hypothesis Tracker) introduced by
Reid in 1979 (Reid, 1979).
2. the JPDAF (Joint Probabilistic Data Association
Filter) introduced by Fortmann, Bar–Shalom and
Scheffe in 1983 (Fortmann et al., 1983).
3. the PMHT (Probabilistic Multi Hypothesis
Tracker) introduced by Streit and Luginbuhl in
1994 (Streit and Luginbuhl, 1994).
Of course, an extension of these algorithms for track-
ing extended crossing objects is straightforward. But
there are several reasons, why such approaches might
fail:
• in most cases there are several measurements from
the same target.
• the crossing can last for a longer time period.
• one of the objects might be occluded by the other
object for some time.
• the objects can accomplish very abrupt maneuvers
during the crossing or especially at the end of the
crossing.
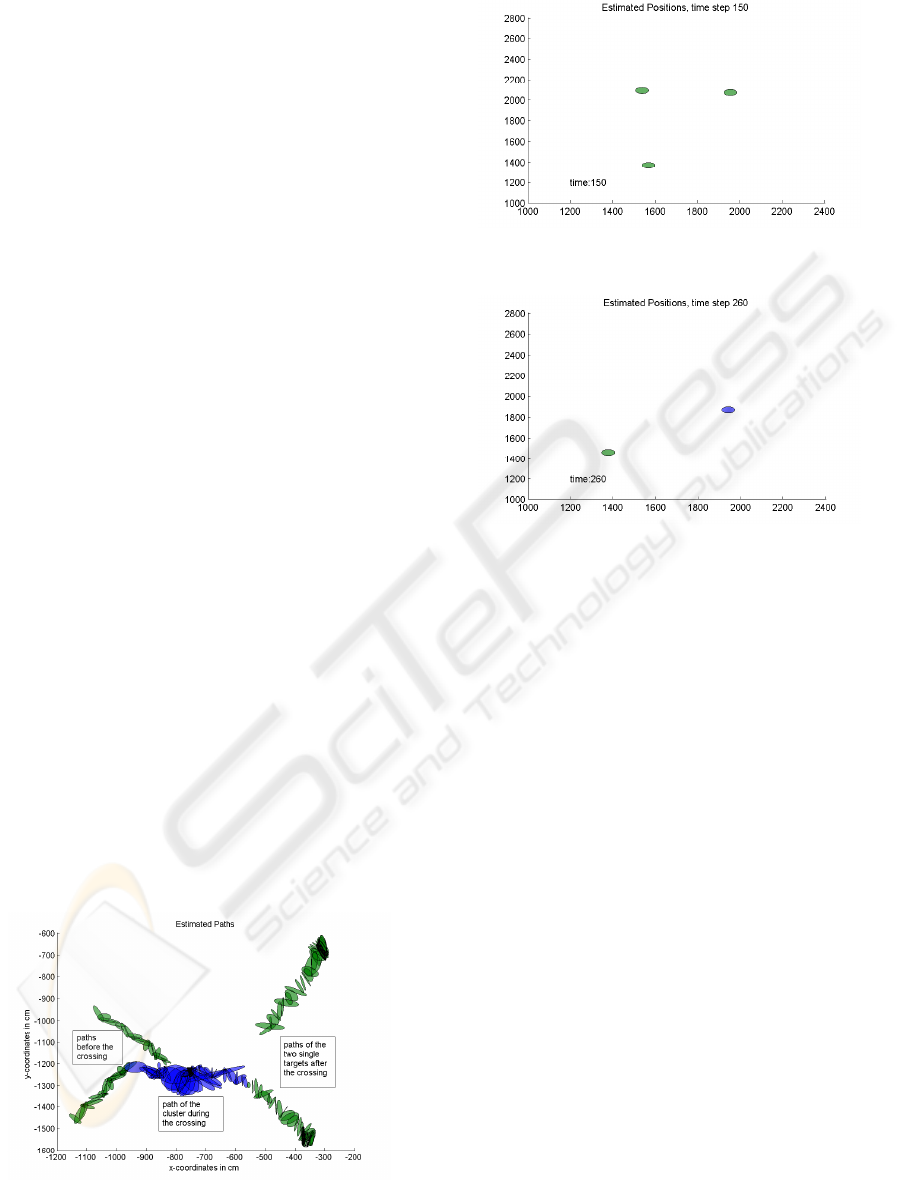
As an example we give the results for an EM based
method (Stannus et al., 2004), which is an exten-
sion of the PMHT (Streit and Luginbuhl, 1994) to
extended targets. Figure 1 shows the results when
applying this algorithm to real data. It shows the es-
Figure 1: Crossing of two objects, real data, EM based
method.
timates for the position of the objects by use of el-
lipses. Thereby the estimated position is the centre
of the ellipse, whereas the shape of the ellipse repre-
sents the actual geometry of the tracked object. The
objects start in the left and move to the right. Ob-
viously, the algorithm looses the one of the targets,
which moves to the upper right after the crossing. See
also figure 2. Moreover, the computational burden for
applying these algorithms is very high when applied
to extended targets, since these objects can be the ori-
gin of up to ten measurements. These difficulties are
well known in the mobile robotics community:
• Tracking moving objects whose trajectories cross
each other is a very general problem ... Problems
of this type cannot be eliminated even by more so-
phisticated methods ... (Prassler et al., 1999).
• Tracks are lost when people walk too closely to-
gether ... (Schumitch et al., 2006).
With respect to these circumstances our research
group has developed a new method that solves the
problem of tracking two extended crossing targets
(Kr
¨
außling et al., 2004b; Kr
¨
außling et al., 2005). Un-
fortunately this algorithm is not able to deal with
more than two crossing objects in its current state.
Therefore, recently our research group has developed
a more general algorithm, which is able to deal with
an arbitrary number of crossing objects, i.e. objects
that get very close to each other. This algorithm is the
main contribution of this work.
The remainder of this paper is organized as follows.
In section 2 the mathematical background including
the used model, the validation gate, and two basic
tracking algorithms are given. In section 3 the new
algorithm for tracking multiple interacting objects is
introduced. Furthermore, in section 4 the experimen-
tal results are presented. Finally, section 5 contains
the conclusions.
2 THE MATHEMATICAL
BACKGROUND OF THE
ALGORITHMS
2.1 The Model
The dynamics of the objects to be observed and the
observation process itself are modeled by a hidden
Gauß–Markov chain with the equations
x
k
= Ax
k−1
+ w
k−1
(1)
and
z
k
= Bx
k
+ v
k
. (2)
x
k
is the object state vector at time k , A is the state
transition matrix, z
k
is the observation vector at time
k and B is the observation matrix. Furthermore, w
k
and v
k
are supposed to be uncorrelated zero mean
white Gaussian noises with covariances Q and R.
Since the motion of a target in the plane has to be
described a two dimensional kinematic model is used.
Therefore, it is
x
k
= (
x
k1
x
k2
˙x
k1
˙x
k2
)
⊤
(3)
with x
k1
and x
k2
the Cartesian coordinates of the tar-
get and ˙x
k1
and ˙x
k2
the corresponding velocities. z
k
just gives the Cartesian coordinates of the target. For
TRACKING MULTIPLE OBJECTS USING THE VITERBI ALGORITHM
19

the coordinates the equation of a movement with con-
stant velocity is holding, i.e. it is
x
k+1,j
= x
kj
+ ∆T ˙x
kj
. (4)
∆T is the time interval between two consecutive mea-
surements. For the progression of the velocities we
use the equation
˙x
k+1,j
= e
−∆T/Θ
˙x
kj
+ Σ
p
1 − e
−2∆T/Θ
u(k) (5)
from (van Keuk, 1971) with the zero mean white
Gaussian noise u(k) with E[u(m)u(n)
⊤
] = δ
mn
.
Thus, the velocity is supposed to decline exponen-
tially. The term
Σ
p
1 − e
−2∆T/Θ
u(k) (6)
models the process noise and the accelerations.
2.2 The Validation Gate
The validation gate is realized using the Kalman filter.
The Kalman filter calculates a prediction y(k + 1|k)
for the measurements z
k+1,l
from the actually hand-
led target at time step k + 1 via the formula
y(k + 1|k) = B · A · x(k|k). (7)
x(k|k) is the estimate for the position of the target at
time step k. For every sensor reading z
k+1,l
of the
time step k + 1 (l = 1, . . . 360) the Mahalanobis dis-
tance λ (Mahalanobis, 1936) with
λ = (z
k+1,l
− y(k + 1|k))
⊤
· [S(k + 1)]
−1
·
·(z
k+1,l
− y(k + 1|k)) (8)
is computed. Then all measurements with λ > λ
max
with a given threshold λ
max
are excluded. See (Bar-
Shalom and Fortmann, 1988) for further details. This
procedure results in a set {ˆz
k+1,i
}
m
k+1
i=1
of m
k+1
se-
lected measurements ˆz
k+1,i
. The matrix S(k + 1) is
the innovations covariance from the Kalman filter. In
common filter applications this matrix is calculated
from the predictions covariance P (k + 1|k) with the
equation
S(k + 1) = BP (k + 1|k)B
⊤
+ R (9)
with the given covariance matrix R of the measure-
ment noise. But for tracking extended objects this ap-
proach is not sufficient, since there is an additional
influence of the extendedness of the object to the
deviation of the measurements from the prediction
y(k + 1|k). To take care of this feature an accessory
positive definite matrix E should be added in equa-
tion 9. Otherwise a lot of the measurements from the
target would be excluded by the gating process. Be-
cause the lateral dimension of people usually shows a
radius in the range of 30 cm, the entries of E should
be in the range of 900. Thus, after some optimization
process we used
E =
780 0
0 780
(10)
and
S(k + 1) = BP (k + 1|k)B
⊤
+ R + E. (11)
The values of the entries of the matrix E vastly ex-
ceed the values of the entries of the matrix R, so that
the main contribution in equation 11 comes from the
matrix E.
2.3 The Kalman Filter Algorithm
with Equal Weights
This algorithm first calculates an unweighted mean
z
k+1
of the m
k+1
measurements {ˆz
k+1,l
}
m
k+1
l=1
, that
have been selected by the gate, i.e. it is
z
k+1
=
1
m
k+1
m
k+1
X
l=1
ˆz
k+1,l
. (12)
This mean is used as the input for the update equation
of the Kalman filter, i.e. it is
x(k+1|k+1) = x(k+1|k)+K
k+1
(z
k+1
−y(k+1|k))
(13)
with the predictions x(k +1|k) and y(k+1|k) and the
Kalman gain K
k+1
derived from the Kalman filter.
Finally, the estimates x(k + 1|k + 1) are further im-
proved by the use of the Kalman smoother (Shumway
and Stoffer, 2000). The corresponding algorithm is
called Kalman filter algorithm (KFA). As has been
shown in (Kr
¨
außling et al., 2005) it is very fast and
gives good information about the position of the tar-
get, but cannot reproduce multimodal probability dis-
tributions. Thus it is not able to handle multiple inter-
acting targets.
2.4 The Viterbi Based Algorithm
The Viterbi algorithm has been introduced in (Viterbi,
1967). A good description is also given in (Forney Jr.,
1973). It has been recommended for tracking puncti-
form targets in clutter in (Quach and Farooq, 1994)
and for tracking extended targets in (Kr
¨
außling et al.,
2004a). It calculates for each selected measurement
ˆz
k+1,i
a separate estimate x(k +1|k +1)
i
. For the cal-
culation of the estimates x(k + 1|k +1)
i
in the update
equation 13 the measurement ˆz
k+1,i
and the predic-
tions x(k + 1|k)
j
and y(k + 1|k)
j
from the predeces-
sor j are used. When tracking punctiform targets in
clutter, the predecessor is determined by minimizing
the length of the paths ending in ˆz
k+1,i
. When regard-
ing extended targets in most cases all measurements
ICINCO 2006 - ROBOTICS AND AUTOMATION
20
in the validation gate are from the target, so that it
is not meaningful to consider the lengths of the paths
ending in the possible predecessors ˆz
k,j
when deter-
mining the predecessor. Therefore, a better choice for
the predecessor is that one for which the Mahalanobis
distance (Mahalanobis, 1936)
ν
⊤
k+1,j,i
[S(k + 1)]
−1
ν
k+1,j,i
(14)
is kept to a minimum. There, ν
k+1,j,i
is the innova-
tion
ν
k+1,j,i
= z
k+1,i
− y(k + 1|k)
j
(15)
and S(k + 1) is the innovations covariance. This pro-
cedure is similar to a nearest neighbour algorithm.
When applying the Viterbi algorithm the application
of the validation gate is performed in the following
way. At first for every selected measurement ˆz
k,j
the
gate is applied to the measurements at time k+1. That
results in the sets Z
k+1,j
of measurements which have
passed the particular gate for the measurement ˆz
k,j
successfully. The set of all measurements ˆz
k+1,i
, that
are associated with the target, is then just the union of
these sets. By this procedure it is ensured, that the cor-
responding tracking algorithms can deal with multi-
modal probability distributions to some extend, which
is a major improvement when dealing with multiple
interacting targets.
The estimates delivered by the Viterbi algorithm
are used as follows. One of these estimates is chosen
as an estimate of the position of a target. This estimate
is the one with index one. Again, different from track-
ing a punctiform target in clutter, it is not meaningful
to make use of the lengths of the paths corresponding
to the estimates and to choose the estimate with the
shortest corresponding path. The corresponding algo-
rithm is called Viterbi based algorithm (VBA) and has
been introduced in (Kr
¨
außling et al., 2004a). The dis-
advantages of this algorithm are a great computational
burden and a poor information about the position of
the tracked objects (Kr
¨
außling et al., 2005).
Figure 2: Two crossing targets.
(a) The algorithm tracks three distinct, moving
targets.
(b) Two of the targets get in close proximity of each
other, and are therefore represented by one cluster.
Figure 3: First Experiment.
3 AN ALGORITHM FOR
TRACKING MULTIPLE
INTERACTING OBJECTS
Our new algorithm uses two classes of objects:
• single targets.
• clusters, which represent at least two interacting
objects, i.e. objects that are moving very close to
each other.
Single targets are tracked with the KFA, since there is
no need for representing multimodal probability dis-
tributions. Furthermore, this algorithm is very fast
and gives very accurate information about the posi-
tion of the tracked object.
Clusters are tracked with the VBA, since multi-
modal distributions have to be represented. This ap-
proach guarantees that none of the objects that are
associated with the cluster is lost. This fact is im-
portant especially when the objects split and start to
move separately again.
Three different events have to be regarded when
tracking multiple interacting objects:
1. The merging of two single targets. This means that
two single targets get very close to each other. This
is the case, if at least one measurement lies in the
TRACKING MULTIPLE OBJECTS USING THE VITERBI ALGORITHM
21

(a) The third target joins the other two and is also as-
sociated with the cluster.
(b) One of the targets separates from the others, thus
we can track subclusters.
Figure 4: First Experiment.
validation gates of both targets. Then the algorithm
stops to track the two single targets with the KFA
and starts tracking a cluster, which contains both
targets, using the VBA. Therefore, it uses the mea-
surements lying in the validation gates of both tar-
gets.
2. The merging of a single target and a cluster. This
means that a single target and a cluster get very
close to each other. This happens, if at least one
measurement lies in the validation gates of the tar-
get and the cluster. In this case the algorithm stops
to track the single target and the cluster separately.
Instead it starts tracking a combined cluster. There-
fore, it uses the measurements lying in the valida-
tion gates of both the single target and the previ-
ously considered cluster.
3. The merging of two clusters. This means that two
clusters get very close to each other. This is the
case, if at least one measurement lies in the val-
idation gates of both clusters. If this is true, the
algorithm stops to track the two clusters and starts
tracking a combined cluster. Therefore, it uses the
measurements lying in the validation gates of both
previously considered clusters.
Note, that whenever a merging takes place, the algo-
rithm remembers the single targets which correspond
to the new combined cluster.
(a) The other two targets also separate and therefore
three subclusters are tracked.
(b) Once these subclusters leave each others proxim-
ity, the single targets can be tracked.
Figure 5: First Experiment.
For each tracked cluster, we have to detect if it dis-
perses into its single targets. For this, we define three
conditions, that are checked by the algorithm:
1. The position estimates corresponding to the mea-
surements in the validation gates are separated into
subclusters. For this purpose, we select the first es-
timate, which then is associated with the first sub-
cluster. For all other estimates associated with the
cluster, the Euclidian distance to the first estimate
is calculated. If this distance is below a certain
threshold, the estimate is associated with the first
subcluster. In our experiments, we set the thresh-
old to 150 cm, which corresponds to the maximum
distance between the legs of a walking person. We
then have to consider the estimates, for which the
Euclidean distance to the first subcluster exceeds
this manually chosen threshold. Using the same
procedure we applied for building the first subclus-
ter, we now construct subclusters until all estimates
are associated with one of these smaller clusters. If
the number of subclusters equals the number of tar-
gets that were merged into this cluster, the first con-
dition for the dispersion of the cluster is fulfilled.
Then, we proceed with step 2.
2. We now check the distance between the subclusters
pairwise. If the distance is above a manually cho-
sen bound, we regard these clusters as separated.
ICINCO 2006 - ROBOTICS AND AUTOMATION
22

(a) The algorithm tracks four distinct, moving tar-
gets.
(b) Two of the targets get in close proximity of each
other, and are therefore represented by one cluster.
Figure 6: Second Experiment.
We chose the value of that bound to be 300 cm. The
second condition is fulfilled, if the number of pairs
of separated subclusters equals
n(n−1)
2
. Thereby, n
is the number of single targets associated with the
cluster. Hence, we are checking if all subclusters
are pairwise separated.
3. Above this, we can separate single subclusters from
the cluster. This follows the same logic as in step
1. Note, the algorithm is not able to determine, how
many targets are represented by a single subcluster.
If conditions 1 and 2 are met, the n subclusters are
associated with the n single targets, that are therefrom
tracked with the KFA. When separating targets from
clusters, we cannot guarantee if the target association
is the same as before merging the targets into the clus-
ter. We believe that there is no solution to this prob-
lem, if we exclusively use anonymous sensors like
laser range finders.
4 EXPERIMENTS
The presented algorithm was tested with real world
data, recorded in our laboratory. In this section we
show the data of two experiments. Before this, figure
(a) The third and fourth target get close to each other
and are also represented by a cluster.
(b) The two clusters join and thus all four targets are
associated with one cluster.
Figure 7: Second Experiment.
2 illustrates how our algorithm works in the case of
two targets using the data from figure 1. In the figures
in this section single targets are indicated by a green
ellipse, whereas clusters are indicated by a blue el-
lipse. As soon as the above mentioned conditions are
met, we are able to track the two targets separately
again.
In the first experiment, three persons moved around
the observer in counterclockwise direction. At first,
these three persons are tracked separately and thus,
the algorithm uses the KFA (figure 3(a)). Then, two
of the single targets get into close proximity of each
other and are therefore merged into one cluster, which
is tracked using the VBA (figure 3(b)). In the next fig-
ure, the third person joins the group and is also asso-
ciated with the cluster. This combined cluster is still
tracked by the VBA (figure 4(a)). Next, the combined
cluster split after a while into two subclusters which
are indicated in figure 4(b). Then, the cluster split into
three subclusters, which are indicated in figure 5(a).
At this stage of the experiment, condition one is met,
but not condition two. Finally, the three persons split
up fulfilling condition two and the persons are tracked
as single targets again (figure 5(b)). Since we are not
able to tell how many targets are associated with a
subcluster in general, only the total number of targets
TRACKING MULTIPLE OBJECTS USING THE VITERBI ALGORITHM
23

(a) The combined cluster splits after a while into two
subclusters, each of them consisting of an unknown
number of targets.
(b) One of the subclusters splits into two subclusters.
Figure 8: Second Experiment.
is known. Thus, we have to wait until all targets are
separated according to the defined conditions before
the algorithm tracks the individual targets using the
KFA.
In the second experiment, we let the algorithm
track four people. All four persons started walking
alone. Consequently, they are tracked independently
using the KFA (figure 6(a)). Then two of them are
walking together and are therefore tracked in a sin-
gle cluster using the VBA (figure 6(b)), whereas the
other two people are still walking separately. In the
next step, the other two persons are also walking to-
gether. The result is that these two are also tracked
using a single cluster and thus, the algorithm tracks
two distinct clusters, each representing two persons
(figure 7(a)). Then, in figure 7(b) all four of them
are walking together, what results in the merging of
the two clusters to one combined cluster, representing
all four persons. Next, this combined cluster splits
into two subclusters, each consisting of an unknown
number of targets (figure 8(a)). In figures 8(b) and
9(a) these subclusters split up into four subclusters.
Finally, condition two is met and therefore the four
targets are tracked individually again (figure 9(b)).
In the experiments, we showed that our algorithm
is able to keep track of all targets for all situations that
can occur when tracking multiple targets:
(a) The targets split after a while and are therefrom
tracked as subclusters.
(b) Then, the targets can be tracked individually.
Figure 9: Second Experiment.
• the merging of two single targets to a cluster.
• the merging of a single target and a cluster.
• the merging of two clusters to a combined cluster.
• the splitting of a cluster into subclusters which are
indicated separately in the graphics.
• the splitting of several targets tracked in a cluster to
single targets.
5 CONCLUSIONS
In this work we presented a novel algorithm for track-
ing multiple extended interacting objects. It consists
of a Kalman filter tracking procedure for tracking sin-
gle targets with high accuracy and low computational
effort, and a Viterbi based method for tracking objects
that are close to each other. The latter part facilitates
clustering to be able to separate the targets correctly
if they split up.
In experiments we showed this algorithm to be ca-
pable of tracking multiple crossing targets without
any restriction. Of course, since we only use laser
range finders, the target association after a crossing
may be interchanged. There are several approaches
that might be investigated to eliminate this drawback:
• different colours of the pairs of trousers people
ICINCO 2006 - ROBOTICS AND AUTOMATION
24

wear might result in different intensities of the re-
flected laser beams.
• people could wear badges sending out for instance
infrared or ultrasound signals which can be re-
ceived by specific sensors to identify the tracked
people (Schulz et al., 2003).
• usually people wear clothing with different colours.
This information could be exploited for the identifi-
cation of the people using a camera network as has
been proposed in (Schumitch et al., 2006).
Since, up to our knowledge, our method is the first
to be able to track several interacting objects without
loss of track, it might be challenging to combine our
approach with one of these attempts.
So far, we only used a non moving observer. In
principle it is possible to extend the method to be suit-
able for moving observers. This is part of the ongoing
research and will be presented in following publica-
tions.
REFERENCES
Bar-Shalom, Y. and Fortmann, T. (1988). Tracking and
Data Association. Academic Press.
Fod, A., Howard, A., and Mataric, M. J. (2002). Laser–
based people tracking. In Proceedings of the IEEE Intl.
Conf. on Robotics and Automation, pages 3024–3029.
Forney Jr., G.-D. (1973). The viterbi algorithm. Proceed-
ings of the IEEE, 61(3):268–278.
Fortmann, T. E., Bar-Shalom, Y., and Scheffe, M. (1983).
Sonar tracking of multiple targets using joint proba-
bilistic data association. IEEE Journal of Oceanic En-
gineering, OE–8(3).
Fuerstenberg, K. C., Linzmeier, D. T., and Dietmayer, K.
C. J. (2002). Pedestrian recognition and tracking of
vehicles using a vehicle based multilayer laserscanner.
In Proceedings of IV 2002, Intelligent Vehicles Sympo-
sium, volume 1, pages 31–35.
Kr
¨
außling, A., Schneider, F. E., and Wildermuth, D.
(2004a). Tracking expanded objects using the viterbi
algorithm. In Proceedings of the IEEE Conference on
Intelligent Systems, Varna, Bulgaria.
Kr
¨
außling, A., Schneider, F. E., and Wildermuth, D.
(2004b). Tracking of extended crossing objects using
the viterbi algorithm. In Proceedings of the 1st In-
ternational Conference on Informatics in Control, Au-
tomation and Robotics (ICINCO).
Kr
¨
außling, A., Schneider, F. E., and Wildermuth, D. (2005).
A switching algorithm for tracking extended targets.
In Proceedings of the 2nd International Conference
on Informatics in Control, Automation and Robotics
(ICINCO), also to be published in the Springer book
of best papers of ICINCO 2005.
Mahalanobis, P. C. (1936). On the generalized distance in
statistics. Proceedings of the National Institute of Sci-
ence, 12:49–55.
Prassler, E., Scholz, J., and Elfes, E. (1999). Tracking peo-
ple in a railway station during rush–hour. In Chris-
tensen, H. I., editor, Computer Vision Systems, volume
1542, pages 162–179. Springer, lecture notes in com-
puter science edition.
Quach, T. and Farooq, M. (1994). Maximum likelihood
track formation with the viterbi algorithm. In Proceed-
ings of the 33rd Conference on Decision and Control,
Lake Buena Vista, Florida.
Reid, D. B. (1979). An algorithm for tracking multiple
targets. IEEE Trans. Automatic Control, AC–24:843–
854.
Schulz, D., Burgard, W., Fox, D., and Cremers, A. B.
(2001). Tracking multiple moving objects with a mo-
bile robot. In Proceedings of the 2001 IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition (CVPR 2001).
Schulz, D., Fox, D., and Hightower, J. (2003). People
tracking with anonymous and id–sensors using rao–
blackwellised particle filters. In Proceedings of the
18th International Joint Conference on Artificial In-
telligence (IJCAI 2003), Acapulco, Mexico.
Schumitch, B., Thrun, S., Bradski, G., and Olukotun, K.
(2006). The information–form data association filter.
In Proceedings of the 2005 Conference on Neural In-
formation Processing Systems (NIPS), MIT Press.
Shumway, R. H. and Stoffer, D. S. (2000). Time Series
Analysis and Its Applications. Springer.
Stannus, W., Koch, W., and Kr
¨
außling, A. (2004). On
robot–borne extended object tracking using the em al-
gorithm. In Proceedings of the 5th Symposium on In-
telligent Autonomous Vehicles, Lisbon, Portugal.
Streit, R. L. and Luginbuhl, T. E. (1994). Maximum like-
lihood method for multi–hypothesis tracking. Signal
and Data Processing of Small Targets, SPIE, 2335.
Thrun, S. (1998). Learning metric-topological maps for in-
door mobile robot navigation. Artificial Intelligence,
99(1):21–71.
van Keuk, G. (1971). Zielverfolgung nach kalman–
anwendung auf elektronisches radar. Technical Report
173, Forschungsinstitut f
¨
ur Funk und Mathematik,
Wachtberg–Werthhoven, Germany.
Viterbi, A. J. (1967). Error bounds for convolutional codes
and an asymptotically optimum decoding algorithm.
IEEE Transactions On Information Theory, IT–13(2).
TRACKING MULTIPLE OBJECTS USING THE VITERBI ALGORITHM
25
