
SEMIOTICS AND HUMAN-ROBOT INTERACTION
Jo
˜
ao Silva Sequeira
Institute for Systems and Robotics, Instituto Superior T
´
ecnico
Av. Rovisco Pais 1, 1049-001 Lisbon, Portugal
Maria Isabel Ribeiro
Institute for Systems and Robotics, Instituto Superior T
´
ecnico
Av. Rovisco Pais 1, 1049-001 Lisbon, Portugal
Keywords:
Semi-autonomous robot, human-robot interaction, semiotics.
Abstract:
This paper describes a robot control architecture supported on a human-robot interaction model obtained
directly from semiotics concepts.
The architecture is composed of a set of objects defined after a semiotic sign model. Simulation experiments
using unicycle robots are presented that illustrate the interactions within a team of robots equipped with skills
similar to those used in human-robot interactions.
1 INTRODUCTION
This paper describes part of an ongoing project
aiming at developing new methodologies for semi-
autonomous robot control that, in some sense, mimic
those used by humans in their relationships. The pa-
per focus (i) in the use of semiotic signs to control
robot motion and (ii) their use in the interaction with
humans. The approach followed defines (i) a set of
objects that capture key features in human-robot and
robot-robot interactions and (ii) an algebraic system
with operators to work on this space of the objects.
In a wide variety of applications of robots, such
as surveillance in wide open areas, rescue missions
in catastrophe scenarios, and working as personal as-
sistants, the interactions among robots and humans
are a key factor in the success of a mission. In such
missions contingency situations may lead a robot to
request external help, often from a human operator,
and hence it seems natural to search for interaction
languages that can be used by both. Furthermore, a
unified framework avoids the development of separate
competences to handle human-robot and robot-robot
interactions.
The numerous robot control architectures proposed
in the literature account for human-robot interac-
tions (HRI) either explicitely through interfaces to
handle external commands, or implicitely, through
task decomposition schemes that map high level mis-
sion goals into motion commands. Examples of cur-
rent architectures developed under such principles can
be found in (Aylett and Barnes, 1998),(Huntsberger
et al., 2003),(Albus, 1987),(Kortenkamp et al., 1999).
If the humans are assumed to have enough knowledge
on the robots and the environment, imperative com-
puter languages can be used for HRI, easily leading to
complex communication schemes. Otherwise, declar-
ative, context dependent, languages, like Haskell, (Pe-
terson et al., 1999) and FROB, (Hager and Peterson,
1999), have been proposed to simulate robot systems
and also as a mean to interact with them. BOBJ
was used in (Goguen, 2003) to illustrate examples on
human-computer interfacing. RoboML, (Makatchev
and Tso, 2000), supported on XML, is an example
of a language explicitly designed for HRI, account-
ing for low complexity programming, communica-
tions and knowledge representation. In (Nicolescu
and Matari
´
c, 2001) the robots are equipped with be-
haviors that convey information on their intentions to
the outside environment. These behaviors represent a
form of implicit communication between agents such
as the robot following a human without having been
told explicitly to do so. This form of communication,
without explicit exchange of data is an example of in-
teraction that can be modeled using semiotics.
Semiotics studies the interactions among humans.
These are often characterized by the loose specifica-
tion of objectives for instance as when a sentence ex-
presses an intention of motion instead of a specific
path. Capturing some of these features, typical of nat-
ural languages, is the aim of this project.
The paper is organised as follows. Section 2
58
Sequeira J. and Ribeiro M. (2006).
SEMIOTICS AND HUMAN-ROBOT INTERACTION.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 58-65
DOI: 10.5220/0001220600580065
Copyright
c
SciTePress

presents key concepts in semiotics to model human-
human interactions and motivates their use to model
human-robot interactions. These concepts are used
in Section 3 to define the building blocks of the pro-
posed architecture. Section 4 presents a set of basic
experiments that demonstrate the use of the semiotic
model developed along the paper. Section 5 presents
the conclusions and future work.
2 A SEMIOTIC PERSPECTIVE
FOR HRI
In general robots and humans work at very different
levels of abstraction. Humans work primarily at high
levels of abstraction whereas robots are commonly
programmed to follow trajectories, hence operating at
a low level of abstraction.
Semiotics is a branch of general philosophy which
studies the interactions among humans, such as the
linguistic ones (see (Chandler, 2003) for an introduc-
tion to semiotics) and hence it is a natural frame-
work where to search for new methodologies to model
human-robot interactions. In addition, this should be
extended to robot-robot interactions yielding a unify-
ing framework to handle any interaction between a
robot and the external environment.
An algebraic formulation for semiotics and its use
in interface design has been presented in (Malcolm
and Goguen, 1998). An application of hypertext the-
ory to world wide web was developed in (Neum
¨
uller,
2000) Machine-machine and human-human interac-
tions over electronic media (such as the Web) have
been addressed in (Codognet, 2002). Semiotics has
been use in intelligent control as the term encompass-
ing the main functions related to knowledge, namely
acquisition, representation, interpretation, transfor-
mation and manipulation (see for instance (Meystel
and Albus, 2002)) and often directly related to the
symbol grounding concept of artificial intelligence.
The idea underlying semiotics is that humans com-
municate among each other (and with the environ-
ment) through signs. Roughly, a sign encapsulates
a meaning, an object, a label and the relations be-
tween them. Sign systems are formed by signs and
the morphisms defined among them (see for instance
(Malcolm and Goguen, 1998) for a definition of sign
system) and hence, under reasonable assumptions on
the existence of identity maps, map composition, and
composition association, can be modeled using cate-
gory theory framework. The following diagram, sug-
gested by the “semiotic triangle” diagram common
in the literature on this area (see for instance (Chan-
dler, 2003)), expresses the relations between the three
components of a sign.
M
L
syntactics
-
syntactics
semantics
-
O
pragmatics
-
M
pragmatics
semantics
(1)
Labels, (L), represent the vehicle through which the
sign is used. Meanings, (M), stand for what the users
understand when referring to the sign. The Objects,
(O), stand for the real objects signs refer to.
The morphisms in diagram (1) represent the dif-
ferent perspectives used in the study of signs. Semi-
otics currently considers three different perspectives:
semantics, pragmatics and syntactics, (Neum
¨
uller,
2000). Semantics deals with the general relations
among the signs. For instance, it defines whether or
not a sign can have multiple meanings. In human-
human interactions amounts to say that different lan-
guage constructs can be interpreted equivalently, that
is as synonyms. Pragmatics handles the hidden mean-
ings that require the agents to perform some infer-
ence on the signs before extracting their real meaning.
Syntactics defines the structural rules that turn the la-
bel into the object the sign stands for. The starred
morphisms are provided only to close the diagrams
(as the “semiotic triangle” is usually represented as
an undirected graph).
3 AN ARCHITECTURE FOR HRI
This section introduces the architecture by first defin-
ing a set of context free objects and operators on this
set that are compatible (in the sense that they can be
identified) with diagram (1). Next, the corresponding
realizations for the free objects are described. The
proposed architecture includes three classes of ob-
jects: motion primitives, operators on the set of mo-
tion primitives and decision making systems (on the
set of motion primitives).
The first free object, named action, defines primi-
tive motions using simple concepts that can be easily
used in a HRI language. The actions represent mo-
tion trends, i.e., an action represents simultaneously a
set of paths that span the same bounded region of the
workspace.
Definition 1 (Free action) Let k be a time index, q
0
the configuration of a robot where the action starts to
be applied and a(q
0
)|
k
the configuration at time k of
a path generated by action a.
SEMIOTICS AND HUMAN-ROBOT INTERACTION
59

A free action is defined by a triple A ≡ (q
0
,a,B
a
)
where B
a
is a compact set and the initial condition of
the action, q
0
, verifies,
q
0
∈ B
a
, (2)
a(q
0
)|
0
= q
0
, (2b)
∃
>
min
: B(q
0
,) ⊆ B
a
, (2c)
with B(q
0
,) a ball of radius centered at q
0
, and
∀
k≥0
a(q
0
)|
k
∈ B
a
. (2d)
Actions are to inclose different paths with similar
(in a wide sense) objectives. Paths that can be con-
sidered semantically equivalent, for instance because
they lead to a successful execution of a mission, may
be enclosed within a single action.
Representing the objects in Definition 1 in the
form of a diagram it is possible to establish a corre-
spondence between (free) actions and signs verifying
model (1),
q
0
semantics
Q
(q
0
,a,B
a
)
semantics
B
-
B
a
A
synctatics
?
pragmatics
B
pragmatics
Q
-
The projection maps semantics
B
and semantics
Q
express the fact that multiple trajectories starting in
a neighborhood of q
0
and lying inside B
a
may lead
to identical results. The pragmatics
B
map expresses
the fact that given a bounding region it may be pos-
sible to infer the action being executed. Similarly,
pragmatics
Q
represents the maps that infer the ac-
tion being executed given the initial condition q
0
. The
synctatics map simply expresses the construction of
an action through Definition 1.
Following model (1), different actions can yield the
same meaning, that is, the two actions can produce the
same net effect in a mission. This amounts to require
that the following diagram commutes,
A
equality
-
A
B
a
semantics
B
?
1
M
B
a
semantics
B
?
(3)
where 1
M
stands for the identity map in the space of
meanings, M.
Diagram (3) provides a roadmap to define action
equality as a key concept to evaluate sign semantics.
Definition 2 (Free action equality) Two actions
(a
1
,B
a
1
,q
0
1
) and (a
2
,B
a
2
,q
0
2
) are equal, the rela-
tion being represented by a
1
(q
0
1
)=a
2
(q
0
2
), if and
only if the following conditions hold
a
1
(q
0
1
),a
2
(q
0
2
) ⊂ B
a
1
∩ B
a
2
(4)
∀
k
2
≥0
, ∃
k
1
≥0
, ∃
:
a
1
(q
0
1
)|
k
1
∈B(a
2
(q
0
2
)|
k
2
,) ⊂ B
a
1
∩ B
a
2
(4b)
Expressions (4) and (4b) define the equality map
in diagram (3). It suffices to choose identical bound-
ing regions (after condition (4)) and a goal region
inside the bounding regions (after condition (4b)) to
where the paths generated by both actions converge.
The realization for the free action of Definition 1 is
given by the following proposition.
Proposition 1 (Action) Let a(q
0
) be a free action.
The paths generated by a(q
0
) are solutions of a sys-
tem in the following form,
˙q ∈ F
a
(q) (5)
where F
a
is a Lipschitzian set-valued map with closed
convex values verifying,
F
a
(q) ⊆ T
B
a
(q) (5b)
where T
B
a
(q) is the contingent cone to B
a
at q (see
(Smirnov, 2002) for the definition of this cone).
The demonstration of this proposition is just a re-
statement, in the context of this paper, of Theorem 5.6
in (Smirnov, 2002) on the existence of invariant sets
for the inclusion (5).
The convexity of the values of the F
a
map must be
accounted for when specifying an action. The Lip-
schitz condition imposes bounds on the growing of
the values of the F
a
map. In practical applications this
assumption can always be verified by proper choice
of the map. This condition is related to the existence
of solutions to (5), namely as it implies upper semi-
continuity (see (Smirnov, 2002), Proposition 2.4).
Proposition 2 (Action identity) Two actions a
1
and
a
2
, implemented as in Proposition 1, are said equal
if,
B
a
1
= B
a
2
(6)
∃
k
0
: ∀
k>k
0
,F
a
1
(q(k)) = F
a
2
(q(k)) (6b)
ICINCO 2006 - ROBOTICS AND AUTOMATION
60

The demonstration follows by direct verification of
the properties in Definition 2.
By assumption, both actions verify the conditions
in Proposition 1 and hence their generated paths are
contained inside B
a
1
∩ B
a
2
which implies that (4) is
verified.
Condition (6b) states that there are always motion
directions that are common to both actions. For ex-
ample, if any of the actions a
1
,a
2
generates paths re-
stricted to F
a
1
∩ F
a
2
then condition (4b) is verified.
When any of the actions generates paths using motion
directions outside F
a
1
∩ F
a
2
then condition (6b) indi-
cates that after time k
0
they will be generated after the
same set of motion directions. Both actions generate
paths contained inside their common bounding region
and hence the generated paths verify (4b).
A sign system is defined by the signs and the mor-
phisms among them. In addition to the equality map,
two other morphisms are defined: action composition
and action expansion.
Definition 3 (Free action composition) Let a
i
(q
0
i
)
and a
j
(q
0
j
) be two free actions. Given a compact
set M, the composition a
j◦i
(q
0
i
)=a
j
(q
0
j
) ◦ a
i
(q
0
i
)
verifies,
if B
a
i
∩ B
a
j
= ∅
a
j◦i
(q
0
i
) ⊂ B
a
i
∪ B
a
j
(7)
B
a
i
∩ B
a
j
⊇ M (7b)
otherwise, the composition is undefined.
Action a
j◦i
(q
0
i
) resembles action a
i
(q
0
i
) up to the
event marking the entrance of the paths into the re-
gion M ⊆ B
a
i
∩ B
a
j
. When the paths leave the
common region M the composed action resembles
a
j
(q
0
j
). While in M the composed action generates
a link path that connects the two parts.
Whenever the composition is undefined the follow-
ing operator can be used to provide additional space
to one of the actions such that the overlapping region
is non empty.
Definition 4 (Free action expansion) Let a
i
(q
0
i
)
and a
j
(q
0
j
) be two actions with initial conditions at
q
0
i
and q
0
j
respectively. The expansion of action a
i
by action a
j
, denoted by a
j
(q
0
j
) a
i
(q
0
i
), verifies
the following properties,
B
ji
= B
j
∪ B
i
, with B
i
∩ B
j
⊆ M (8)
where M is a compact set representing the minimal
amount of space required for the robot to maneuver
and such that the following property holds
∃
q
0
k
∈B
j
: a
i
(q
0
i
)=a
j
(q
0
k
) (8b)
meaning that after having reached a neighborhood of
q
0
k
, a
i
(q
i
) behaves like a
j
(q
j
).
Given the realization (1) chosen for the actions, the
composition and expansion operators can be realized
through the following propositions.
Proposition 3 (Action composition) Let a
i
and a
j
be two actions defined by the inclusions
˙q
i
∈ F
i
(q
i
) and ˙q
j
∈ F
j
(q
j
)
with initial conditions q
0
i
and q
0
j
, respectively. The
action a
j◦i
(q
0
i
) is generated by ˙q ∈ F
j◦i
(q), with the
map F
j◦i
given by
F
j◦i
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
F
i
(q
i
) if q B
i
\M (3)
F
i
(q
i
) ∩ F
j
(q
j
) if q ∈ M (3b)
F
j
(q
j
) if q ∈ B
j
\M (3c)
∅ if B
i
∩ B
j
= ∅ (3d)
for some M ⊂ B
j
∩ B
i
.
Outside M the values of F
i
and F
j
verify the con-
ditions in Proposition 1. Whenever q ∈ M then
F
i
(q
i
) ∩ F
j
(q
j
) ⊂ T
B
j
(q).
The first trunk of the resulting path, given by (3),
corresponds to the path generated by action a
i
(q
0
i
)
prior to the event that determines the composition.
The second trunk, given by (3b), links the paths gen-
erated by each of the actions. Note that by imposing
that F
i
(q
i
) ∩ F
j
(q
j
) ⊂ T
B
j
(q
j
) the link paths can
move out of the region M. The third trunk, given
by (3c), corresponds to the path generated by action
a
j
(q
0
j
).
By Proposition 1, each of the trunks is guaranteed
to generate a path inside the respective bounding re-
gion and hence the overall path verifies (7).
The action composition in Proposition 3 generates
actions that resemble each individual action outside
the overlapping region. Inside the overlapping area
the link path is built from motion directions common
to both actions being composed. The crossing of the
boundary of M defines the events marking the transi-
tion between the trunks.
Whenever F
i
(q
i
) ∩ F
j
(q
j
)=∅ it is still possible
to generate a link path, provided that M has enough
space for maneuvering. The basic idea, presented in
the following proposition, is to locally enlarge either
F
i
(q
i
) or F
j
(q
j
).
Proposition 4 (Action expansion) Let a
i
and a
j
be
two actions defined after the inclusions
˙q
i
∈ F
i
(q
i
) and ˙q
j
∈ F
j
(q
j
)
SEMIOTICS AND HUMAN-ROBOT INTERACTION
61
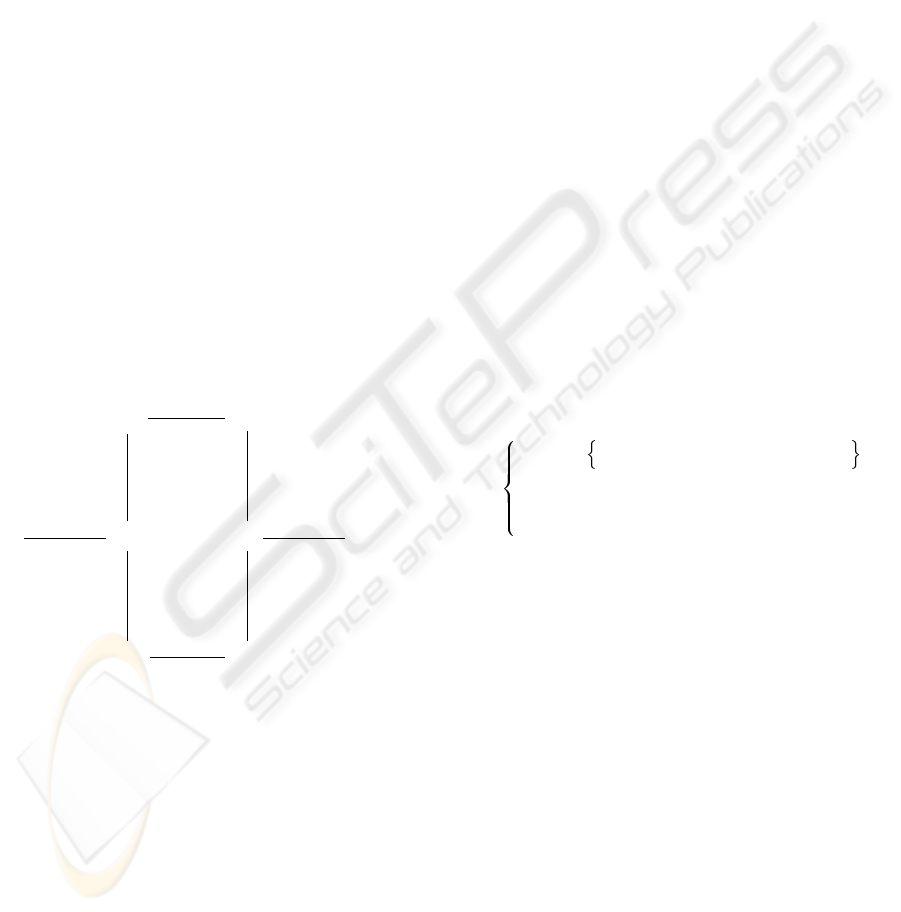
The expansion a
ji
(q
0
i
) verifies the following prop-
erties
F
ij
=
F
i
if q B
i
\M (9)
F
j
∪ F
i
if q ∈ B
i
∩ B
j
∪ M (9b)
where M ⊇ B
i
∩B
j
is the expansion set chosen large
enough such that F
j
∪ F
i
verifies (5b).
Condition (9) generates paths corresponding to the
action a
i
(q
0
i
). These paths last until an event, trig-
gered by the crossing of the boundary of M, is de-
tected. This crossing determines an event that ex-
pands the overall bounding region by M and the set
of paths, by F
j
, as expressed by (9b).
Assuming that F
j
∪ F
i
⊂ T
B
i
∩B
j
∪M
, that is, it
verifies (5b), the complete path is entirely contained
inside the expanded bounding region. After moving
outside M paths behave as of generated by action a
i
,
as required by (8b).
Instead of computing a priori M, the expansion op-
erator can be defined as a process by which action
a
i
converges to action a
j
in the sense that F
i
(q
i
) →
F
j
(q
j
) and M is the space spanned by this process.
The objects and operators defined above are com-
bined in the following diagram,
A
◦
=
-
A
A
=
-
A
s
◦
6
A
◦
?
=
-
A
A
s
?
=
-
A
6
(9)
where A stands for the set of actions available to the
robot, A
◦
and A
stand for the sets of actions rep-
resenting primitive motions used in composition and
expansion, respectively.
The product like part (in the lefthand part) of dia-
gram (9) represents the supervision strategy that de-
termines which of the action sets, A
◦
or A
, is se-
lected at each event. This strategy is mission depen-
dent and is detailed in the s
◦
and s
maps.
4 EXPERIMENTAL RESULTS
This section presents two basic simulation experi-
ments using a team of three unicycle robots and an
experiment with a single real unicycle robot.
Missions are specified through goal regions the ro-
bots have to reach. This resembles a typical human-
robot interaction, with the human specifying a mo-
tion trend the robot has to follow through the goal
region. Furthermore, intuitive bounding regions are
easily constructed from them. The human operator is
thus not explicitely present in the experiments. Nev-
ertheless, as results clear from the third experiment
(with the real robot) there is no lack of generality.
Interactions among the teammates are made
through the action bounding regions, that is each ro-
bot has access to the bounding region being used by
any teammate.
The robots use a single action, denoted a
◦
, defined
as
a
◦
=
F (q)=(G − q) ∩ H(q)
B(q)={p|p = q + αG(q),α∈ [0, 1]}
(10)
where q is the configuration of the robot, G stands for
a goal set, and H(q) stands for the set of admissible
motion directions at configuration q (easily obtained
from the well known kinematics model of the uni-
cycle). This action simply yields a motion direction
pointing straight to the goal set from the current robot
configuration. Whenever there are no admissible con-
trols, i.e., the set of admissible motion directions that
lead straight to the goal region is empty, F (q)=∅,
the bounding region is expanded using the action
a
=
H
i
(q) ∪
set of motion
directions
| d(H
i
,G− q) → 0
if q B
i
\M
F
i
(q) otherwise
where d(, ) stands for a distance between the sets in
the arguments. This action corresponds to having
H(q) converging to G − q. Generic algorithms al-
ready described in the literature can be used obtain
this sort of convergence. The same set of actions and
the supervisor maps is used by all the robots.
In the simulation experiments robots have access to
a synthetic image representing a top view of the en-
vironment and start their mission at the lower part of
the image. The irregular shape in the upper part of
the images shown in the following sections represents
the raw mission goal region to be reached by the ro-
bots. Basic image processing techniques are used to
extract a circle goal region, centered at the centroid
of the convex hull of the countour of these shapes.
This circle is shown in light colour superimposed on
the corresponding shape. The simulations were im-
plemented as a multi-thread system. Each robot sim-
ulator thread runs at an average 100 Hz whereas the
architecture thread runs at an average 80 Hz. Exper-
iments data is recorded by an independent thread at
100 Hz.
ICINCO 2006 - ROBOTICS AND AUTOMATION
62

In the real experiment, the image data is used only
to extract a goal region for the robot to reach. The
navigation relies on odometry data.
4.1 Mission 1
The purpose of this experiment is to assess the behav-
ior of the team when each robot operates isolatedly.
Each robot tries to reach the same goal region (in the
upper righthand side of the image). No information
is exchanged between the teammates and no obstacle
avoidance behaviors are considered. In the simulation
experiments robots 1 and 2 start with a 0 rad orienta-
tion whereas robot 0 starts with π rad orientation.
Figure 1 shows the trajectories generated by the ro-
bots. The symbol ◦ marks the position of each robot
along the mission. Dashed lines connect the time re-
lated robot position marks.
The supervisor maps were chosen as,
s
◦
≡ a
◦
if H(q) ∩ G − q = ∅
s
≡ a
if H(q) ∩ G − q = ∅
(11)
The oscilations in all the trajectories in Figure 1
result from the algorithm used to expand the action
bounding region at the initial time as the initial con-
figuration of any of the robots does not point straight
to the goal set.
x
y
Robots trajectories
50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
robot 2
robot 1
robot 0
goal region
Figure 1: Independent robots.
4.2 Mission 2
The robots have no physical dimensions but close po-
sitions are to be avoided during the travel. This con-
dition is relaxed as soon as the robot reaches the goal
set, that is, once a robot reaches the goal region and
stops the others will continue trying to reach the goal
independently of the distance between them.
The supervisor maps are identical to the previous
mission. However, the co-domain of s
◦
, the set A
◦
,
is changed to account for the interactions among the
robots.
A
i
◦
=
F
i
(q
i
)=
G
i
− q
i
∩ H
i
(q
i
)
B
i
(q
i
)\∪
j=i
B
j
(q
j
)
(12)
where the superscript indicates the robot the action
belongs to.
Actions in (12) use a subset of the motion direc-
tions in (10). The bounding region is constructed
from that in (10) including the information from
the motion trend of the teammates by removing any
points belonging also to that of the teammates. The
original mission goal is replaced by intermediate goal
regions, G
i
, placed inside the new bounding region.
As the robots progress towards these intermediate
goals they also approach the original mission goal. A
potential drawback of this simple strategy is that the
smaller bounding region constrains significatively the
trajectories generated.
Figure 2 illustrates the behavior of the team when
the robots interact using the actions (12). The global
pattern of the trajectories shown is that of a line for-
mation. Once the robots approach the goal region the
distance between them is allowed to decrease so that
each of them can reach the goal.
x
y
Robots trajectories
50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
robot 2
robot 1
robot 0
goal region
Figure 2: Interacting robots.
Figure 3 illustrates the behavior of the team when
a static obstacle is present in the environment. Sim-
ilarly to common path planning schemes used in ro-
botics, an intermediate goal region is chosen far from
the obstacle such that the new action bounding region
allows the robots to move around the obstacle.
From the beginning of the mission robots 0 and 1
find the obstacle in their way to the goal region and
select the intermediate goal shown in the figure. Af-
ter the initial stage where the robots use the expansion
SEMIOTICS AND HUMAN-ROBOT INTERACTION
63

action aiming at aligning their trajectories with the di-
rection of the goal. The interaction that results from
the exchange of bounding regions is visible similarly
as in the previous experiment. Robot 2 is not con-
strained by the obstacle and proceeds straight to the
goal. Its influence in the trajectories of the teammates
around the intermediate goal region is visible in the
long dash lines connecting its position with those of
the teammates.
x
y
Robots trajectories
50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
robot 2
robot 1
robot 0
obstacle
goal region
intermediate
goal region
Figure 3: Interacting robots in the presence of a static ob-
stacle.
4.3 Mission 3
This experiment, with a single robot, aims at validat-
ing the assessment of the framework done, in simula-
tion, in Sections 4.1 and 4.2. The supervisor maps are
those in (11).
Figure 4 shows the Scout robot and the goal re-
gion as extracted using basic color segmentation pro-
cedures. No obstacles were considered in this experi-
ment.
The corresponding trajectory in the workspace is
shown in Figure 5. The robot starts the mission with
orientation π/2, facing the goal region, and hence
maneuvering is not required. The robot proceeds di-
rectly towards the goal region. Figure 6 displays the
trajectory when the robot is made to wander around
the environment. Goal regions are defined at random
instants and when detected by the robot its behavior
changes to the goal region pursuing. The plot shows
the positions of the robot when the targets were de-
tected and when they are reached (within a 5cm error
distance). The visual quality of these trajectories is
close to those obtained in simulation which in a sense
validates the simulations.
Figure 4: A goal region defined over an object in a labora-
tory scenario.
0.5 1 1.5 2 2.5 3 3.
5
1
2
3
4
5
6
7
8
9
y (m)
x (m)
SIB_log5 trajectory
starting region
goal region
Figure 5: Moving towards a goal region.
0 1 2 3 4 5 6
7
0
2
4
6
8
10
12
14
16
SIB_log_full trajectory
y (m)
x (m)
target 1
detected
target 2
detected
target 1
reached
target 2
reached
Figure 6: Moving betwen multiple goals regions.
ICINCO 2006 - ROBOTICS AND AUTOMATION
64

5 CONCLUSIONS
The paper presented an algebraic framework to model
HRI supported on semiotics principles. The frame-
work handles in a unified way any interaction related
to locomotion between a robot and its external envi-
ronment.
The resulting architecture (see Figure 9) has close
connections with multiple other proposals in the liter-
ature, namely in that a low level control layer and a
supervision layer can be easily identified.
Although the initial configurations do not promote
straight line motion, the simulation experiments pre-
sented show trajectories without any harsh maneuver-
ing. The experiment with the real robot validates the
simulation results in the sense that in both situations
identical actions are used and the trajectories obtained
show similar visual quality.
Future work includes (i) analytical study of control-
lability properties in the framework of hybrid systems
with the continuous state dynamics given by differ-
ential inclusions, (ii) the study of the intrinsic prop-
erties for the supervisor building block, currently im-
plemented as a finite state automata, that may sim-
plify design procedures, and (iii) the development of
a basic form of natural language for interaction with
robots given the intuitive meanings that can be given
to the objects in the framework.
ACKNOWLEDGEMENTS
This work was supported by the FCT project
POSI/SRI/40999/2001 - SACOR and Programa Op-
eracional Sociedade de Informac¸
˜
ao (POSI) in the
frame of QCA III.
REFERENCES
Albus, J. (1987). A control system architecture for intelli-
gent systems. In Procs. of the 1987 IEEE Intl. Conf.
on Systems, Man and Cybernetics. Alexandria, VA.
Aylett, R. and Barnes, D. (1998). A multi-robot architec-
ture for planetary rovers. In Procs. of the 5th Eu-
ropean Space Agency Workshop on Advanced Space
Technologies for Robotics & Automation. ESTEC,
The Netherlands.
Chandler, D. (2003). Semiotics, The basics. Rutledge.
Codognet, P. (2002). The semiotics of the web. In
Leonardo, volume 35(1). The MIT Press.
Goguen, J. (2003). Semiotic morphisms, representations
and blending for interface design. In Procs of the
AMAST Workshop on Algebraic Methods in Language
Processing. Verona, Italy, August 25-27.
Hager, G. and Peterson, J. (1999). Frob: A transformational
approach to the design of robot software. In Procs.
of the 9th Int. Symp. of Robotics Research, ISRR’99.
Snowbird, Utah, USA, October 9-12.
Huntsberger, T., Pirjanian, P., Trebi-Ollennu, A., Nayar, H.,
Aghazarian, H., Ganino, A., Garrett, M., Joshi, S., and
Schenker, P. (2003). Campout: A control architecture
for tightly coupled coordination of multi-robot sys-
tems for planetary surface exploration. IEEE Trans.
Systems, Man & Cybernetics, Part A: Systems and Hu-
mans, 33(5):550–559. Special Issue on Collective In-
telligence.
Kortenkamp, D., Burridge, R., Bonasso, R., Schrekenghost,
D., and Hudson, M. (1999). An intelligent software
architecture for semi-autonomous robot control. In
Procs. 3rd Int. Conf. on Autonomous Agents - Work-
shop on Autonomy Control Software.
Makatchev, M. and Tso, S. (2000). Human-robot interface
using agents communicating in an xml-based markup
language. In Procs. of the IEEE Int. Workshop on Ro-
bot and Human Interactive Communication. Osaka,
Japan, September 27-29.
Malcolm, G. and Goguen, J. (1998). Signs and representa-
tions: Semiotics for user interface design. In Procs.
Workshop in Computing, pages 163–172. Springer.
Liverpool, UK.
Meystel, A. and Albus, J. (2002). Intelligent Systems: Ar-
chitecture, Design, and Control. Wiley Series on In-
telligent Systems. J. Wiley and Sons.
Neum
¨
uller, M. (2000). Applying computer semiotics to hy-
pertext theory and the world wide web. In Reich, S.
and Anderson, K., editors, Procs. of the 6th Int. Work-
shop and the 6th Int. Workshop on Open Hypertext
Systems and Structural Computing, Lecture Notes in
Computer Science, pages 57–65. Springer-Verlag.
Nicolescu, M. and Matari
´
c, M. (2001). Learning and inter-
acting in human-robot domains. IEEE Transactions
on Systems, Man, and Cybernetics, Part A: Systems
and Humans, 31(5):419–430.
Peterson, J., Hudak, P., and Elliott, C. (1999). Lambda in
motion: Controlling robots with haskell. In First In-
ternational Workshop on Practical Aspects of Declar-
ative Languages (PADL).
Smirnov, G. (2002). Introduction to the Theory of Differ-
ential Inclusions, volume 41 of Graduate Studies in
Mathematics. American Mathematical Society.
SEMIOTICS AND HUMAN-ROBOT INTERACTION
65
