DYNAMIC PARAMETERS IDENTIFICATION OF AN
OMNI-DIRECTIONAL MOBILE ROBOT
Andr
´
e Scolari Conceic¸
˜
ao, A. Paulo Moreira, Paulo J. Costa
Department of Electrical and Computer Engineering
University of Porto - Porto - Portugal.
Keywords:
Mobile robots, model and identification systems, simulations.
Abstract:
This paper presents the experimental dynamic parameters identification of an omni-directional mobile robot
with four wheels. Three methods of parameters identification related to dynamic equations are described, the
parameters are the viscous frictions, the coulomb frictions and the inertia moment of the robot. A simulation
environment, simulation results and real results are presented.
1 INTRODUCTION
Dynamic modelling of mobile robots is very impor-
tant to design of controllers, mainly when the ro-
bots need to travel at higher velocity and perform
heavy works. For example, in (Liu et al., 2003)
and (Watanabe, 1998), control strategies for omni-
directional robots using the dynamic model are dis-
cussed. However, non-linearities, like motor dynamic
constraints can greatly affect the robot behaviour, es-
pecially when the robot is accelerated and deceler-
ated. This paper presents a robot model identifica-
tion that could find the non-linear saturation elements.
Three methods are described to identification of the
model’s parameters.
We focus attention on a omni-directional mobile
robot with four motors, as shown in Fig.1(a), built
for the 5dpo Robotic Soccer team from the Depart-
ment of Electrical and Computer Engineering at the
University of Porto at Porto, Portugal. For this ap-
plication (Robotic Soccer) the mobile robot needs to
execute trajectories quickly and with a perfect posi-
tion to the objective, for example, positioning to the
ball, or to the goal, or to avoid dynamic obstacles. So,
the dynamic characteristics of the motion are essential
to follows the path correctly.
In section 2, the omni-directional mobile robot
model is developed. The experimental methods of
identification to model’s parameters is presented in
section 3. In section 4, simulation environment, simu-
lation and real results of the identified model are pre-
sented. Finally, the conclusion and future works are
drawn in section 5.
2 THE MOBILE ROBOT MODEL
The omni-directional mobile robot model is develo-
ped based on the dynamics, kinematics and DC mo-
tors of the robot.
(a) Mobile robot. (b) Geometric parameters
and coordinate frames.
Figure 1: Omni-Directional robot.
The World frame (X, Y, θ), the robot’s body frame
and the geometric parameters are shown in Fig. 1(b).
The following symbols, in SI unit system, are used to
modelling:
• b [m] → distance between the point P(center of chassis)
and robot’s wheels
565
Conceição A., Moreira A. and Costa P. (2006).
DYNAMIC PARAMETERS IDENTIFICATION OF AN OMNI-DIRECTIONAL MOBILE ROBOT.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 565-570
DOI: 10.5220/0001220805650570
Copyright
c
 SciTePress

• M [kg] → robot mass
• r [m] → wheel radius
• l → motor reduction
• J [kg.m
2
] → robot inertia moment
• B
v
, B
vn
[N/(m/s)] → viscous friction related to V
and V
n
velocities
• B
w
[N/(rad/s)] → viscous friction related to W velo-
city
• C
v
, C
vn
[N] → coulomb friction related to V and V
n
velocities
• C
w
[N.m] → coulomb friction related to W velocity
• V, V
n
[m/s] → linear velocities of the robot
• W [rad/s] → angular velocity of the robot
• θ [rad] → orientation angle of the robot
• F
v
, F
vn
[N] → traction forces of the robot
• Γ [N.m] → rotation torque of the robot
• v
1
, v
2
, v
3
, v
4
[m/s] → wheels linear velocities
• f
1
, f
2
, f
3
, f
4
[N] → wheels traction forces
• T
1
, T
2
, T
3
, T
4
[N.m] → wheels rotation torque
2.1 Robot Dynamics
By Newton’s law of motion and the robot’s body
frame, in Fig. 1(b), we have
F
v
(t) = M
dV (t)
dt
+ B
v
V (t) + C
v
sgn(V (t)) (1)
F
vn
(t) = M
dV n(t)
dt
+ B
vn
V
n
(t) + C
vn
sgn(V
n
(t))
(2)
Γ(t) = J
dW (t)
dt
+ B
w
W (t) + C
w
sgn(W (t)) (3)
where,
sgn(α) =
(
1, α > 0,
0, α = 0,
−1, α < 0.
The relationships between the robot’s traction
forces and the wheel’s traction forces are,
F
v
(t) = f
4
(t) − f
2
(t) (4)
F
v n
(t) = f
1
(t) − f
3
(t) (5)
Γ(t) = (f
1
(t) + f
2
(t) + f
3
(t) + f
4
(t))b (6)
The wheel’s traction force(f) and the wheel’s
torque(T ), for of each DC motor, is as follow:
f(t) =
T (t)
r
(7)
T (t) = l.K
t
.i
a
(t) (8)
where i
a
(t) is the armature current and K
t
is motor
torque constant. The dynamics of each DC motor can
be described using the following equations,
u(t) = L
a
di
a
(t)
dt
+ R
a
i
a
(t) + K
v
w
m
(t) (9)
T (t) = K
t
i
a
(t) (10)
where L
a
is the armature inductance, R
a
is the ar-
mature resistance, u(t) is the applied armature vol-
tage, w
m
(t) is the rotor angular velocity in rad/sec,
k
v
is the emf constant.
2.2 Robot Kinematics
By geometric parameters of the robot and the robot’s
body frame, in Fig. 1(b), it is possible to derive the
motion equations,
dx(t)
dt
= V (t)cos(θ(t)) − V n(t)sen(θ (t))
dy ( t)
dt
= V (t)sen(θ(t)) + V n(t)cos(θ(t))
dθ(t)
dt
= W (t)
(11)
The relationships between wheel’s linear velocities
(v
1
, v
2
, v
3
and v
4
) and robot velocities (V ,V n and
W ) are,
v
1
(t) = V
n
(t) + bW (t)
v
2
(t) = −V (t) + bW (t)
v
3
(t) = −V
n
(t) + bW (t)
v
4
(t) = V (t) + bW (t)
(12)
Where x(t) and y(t) is the localization of the point
P , and θ(t) the orientation angle of the robot.
3 MODEL’S PARAMETERS
IDENTIFICATION
The parameters related to dynamic equations of the
mobile robot were experimentally identified. The
parameters are the viscous frictions (B
v
, B
v n
, B
w
),
the coulomb frictions (C
v
, C
v n
, C
w
) and the inertia
moment(J) of the mobile robot. The robot mass was
balanced(M = 35kg). Three methods were used
to identify the parameters, which are detailed in the
next subsections. The coulomb and viscous frictions
were identified with the methods 1 and 2. The inertia
moment was identified by two ways: combining the
method 1 with the method 2, and with the method 3.
Thus, we used two methods for identify the frictions(1
and 2) and two methods(1+2 and 3) for identify the
inertia moment.
3.1 Method 1 - Robot on Steady
State Velocity
This method was used to identify the viscous
frictions (B
v
, B
v n
, B
w
) and the coulomb frictions
ICINCO 2006 - ROBOTICS AND AUTOMATION
566

(C
v
, C
v n
, C
w
) of the mobile robot. This method
consists of apply velocities V , V
n
and W in robot,
and measure the traction forces(F
v
, F
v n
) and the
torque(Γ), with the robot on steady state velocity. Due
to steady state velocity (null derivatives) and for posi-
tive velocities, we can simplify the equations 1, 2 and
3:
F
v
(t) = B
v
V (t) + C
v
(13)
F
v n
(t) = B
v n
V
n
(t) + C
v n
(14)
Γ(t) = B
w
W (t) + C
w
(15)
Three experiments had been made, for V , V
n
and
W separately. The experiment consists in apply four
velocities and measure the traction forces and the
torque. The table 1 shows the applied velocities and
the resulting forces and torque. The forces and torque
were calculated based in the motor’s currents, using
the set of equations 4...8. The velocities and cur-
rents of the first, second and third experiments for
V = 1(m/s), V
n
= 1(m/s) and W = 1(rad/s),
are shown in Figs. 2, 3 and 4.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Speed V
time[sec]
V [m/s]
V=1 [m/s]
(a) V = 1 (m/s)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−6
−4
−2
0
2
4
6
Currents i2,i4
time[sec]
I[A]
i2
i4
(b) i
a
2, i
a
4 (A)
Figure 2: Velocity and currents - first experiment.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Speed Vn
time[sec]
Vn [m/s]
Vn=1 [m/s]
(a) V n = 1 (m/s)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−6
−4
−2
0
2
4
6
Currents i1,i3
time[sec]
I[A]
i1
i3
(b) i
a
1, i
a
3 (A)
Figure 3: Velocity and currents - second experiment.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Speed W
time[sec]
W [rad/s]
W=1
(a) W = 1 (rad/s)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.5
1
1.5
2
2.5
Currents i1,i2,i3,i4
time[sec]
I[A]
i1
i2
i3
i4
(b) i
a
1, i
a
2, i
a
3, i
a
4 (A)
Figure 4: Velocity and currents - third experiment.
Since we have the values for velocities and forces,
we can estimate the viscous and coulomb frictions.
Table 1: Applied velocities and resulting forces and torque.
V F
v
V
n
F
vn
W Γ
(m/s) (N) (m/s) (N) (rad/s) (N.m)
0.6 30.585 0.6 30.285 0.6 5.556
0.8 31.459 0.8 30.814 0.8 5.730
1 31.874 1 31.174 1 5.842
1.2 32.765 1.2 32.106 1.2 6.009
The least-squares line method was used to approxi-
mate the set of data to a linear model(y = ax+ b). The
Fig. 5 shows the applied velocities, resulting forces
and the best fitting line. The resulting equations and
the frictions are presented in the table 2.
Table 2: Resulting equations and frictions - method 1.
Equations B
v
,B
vn
C
v
,C
vn
B
w
C
w
V F
v
(t) = 3.45V (t) + 28.55 3.45 28.55
V
n
F
vn
(t) = 2.90V
n
(t) + 28.46 2.90 28.46
W Γ(t) = 0.73W (t) + 5.12 0.73 5.12
0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4
30.5
31
31.5
32
32.5
33
V[m/s]
Fv[N]
(a) F
v
= f(V )
0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4
30.2
30.4
30.6
30.8
31
31.2
31.4
31.6
31.8
32
32.2
Vn[m/s]
Fvn[N]
(b) F
vn
= f(V
n
)
0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4
5.55
5.6
5.65
5.7
5.75
5.8
5.85
5.9
5.95
6
6.05
W[rad/s]
T[Nm]
(c) Γ = f(W )
Figure 5: Forces and torque vs. velocities.
3.2 Method 2 - Robot with Null
Traction Forces
In this method, the velocity variation with null
traction forces was used to estimate the viscous
frictions(B
v
and B
v n
), the coulomb frictions (C
v
and
C
v n
) and the inertia moment J of the robot. Firstly,
a constant velocity was applied on the robot, and then
the robot motors were turned off, which resulted in
null currents and null forces, consequently, provoking
a velocity decrease until the robot stopped.
From the equations 1, 2 and 3 with null forces and
null torque, we have the following equations for posi-
tive velocities:
dV (t)
dt
= −
B
v
M
V (t) −
C
v
M
(16)
dV n(t)
dt
= −
B
v n
M
V
n
(t) −
C
v n
M
(17)
dW (t)
dt
= −
B
w
J
W (t) −
C
w
J
(18)
DYNAMIC PARAMETERS IDENTIFICATION OF AN OMNI-DIRECTIONAL MOBILE ROBOT
567

Three experiments had been made, for V , V
n
and
W separately, see Fig. 6. The accelerations(
dV
dt
,
dV
n
dt
and
dW
dt
) were calculated from the velocities(V ,
V
n
and W ), using the Euler’s method(Franklin et al.,
1997)). We used the range of data, where the forces
and torque were null to estimate the parameters, as in
Fig.7.
0 10 20 30 40 50 60 70 80
0
0.5
1
1.5
V[m/s]
Samples
(a) V (t)(m/s)
0 10 20 30 40 50 60 70 80
0
0.2
0.4
0.6
0.8
1
Vn[m/s]
Samples
(b) V
n
(t)(m/s)
0 10 20 30 40 50 60 70 80
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
W[rad/s]
Samples
(c) W (t)(rad/s)
Figure 6: Velocities behaviour.
0 5 10 15 20 25 30 35
−1.5
−1
−0.5
0
0.5
1
1.5
Samples
Velocity [m/s]
Acceleration[m/s.s]
(a) V (t),
dV (t)
dt
0 5 10 15 20 25
−1.5
−1
−0.5
0
0.5
1
Samples
Velocity[m/s]
Acceleration[m/s.s]
(b) V
n
(t),
dV
n
(t)
dt
0 2 4 6 8 10 12
−6
−5
−4
−3
−2
−1
0
1
2
3
Samples
Velocity[rad/s]
Aceleration[rad/s.s]
(c) W (t),
dW (t)
dt
Figure 7: Velocities and accelerations.
In order to estimate the viscous and the coulomb
frictions, the mass M and the inertia moment J
values are necessary. As there is no inertia mo-
ment J value, an estimation of J was firstly ob-
tained. We used the equation 18, the velocity curve
W (t) and the acceleration curve
dW (t)
dt
shown in Fig.
7(c). The viscous(B
w
) and the coulomb(C
w
) fric-
tions, estimated with method 1, were used on equa-
tion 18. The estimated robot inertia moment was
J = 1.358[kg.m
2
].
Since we have the values of robot mass, velo-
city and acceleration, we can apply on equations 16
and 17, to obtain viscous frictions(B
v
and B
v n
) and
coulomb frictions (C
v
and C
v n
). The table 3 shows
the equations obtained through least-squares method
and the friction values.
Table 3: Resulting equations and frictions - method 2.
Equations B
v
, C
v
,
B
vn
C
vn
V
dV (t)
dt
= −0.11V (t) − 0.86
4.01 30.35
V
n
dV n(t)
dt
= −0.10V
n
(t) − 0.87
3.77 30.76
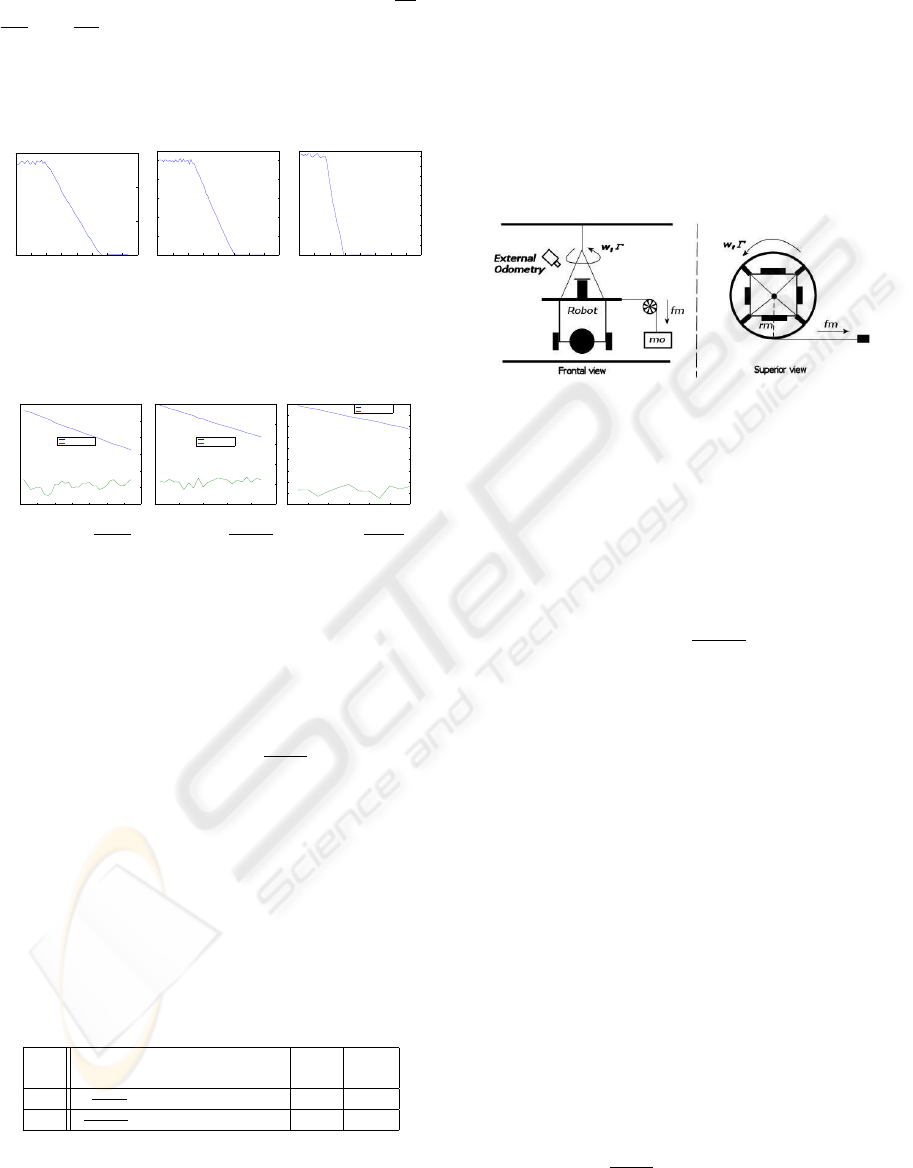
3.3 Method 3 - Inertia Moment
Identification
A practical method for estimating the moment of iner-
tia J of the robot, to compare with the estimation
of the methods 1+2, is presented. The robot was
hanged from the ceiling by wire, see figure 8, to eli-
minate frictions between the robot and the floor. The
mass(m
o
) was hanged at the disc attached to the ro-
bot, by a wire.
Figure 8: Schematic of the experience.
By applying a known torque(Γ(t)) to robot body,
and measuring the resultant angular position(θ(t)), by
a external odometry system based on vision, we can
compute the moment of inertia of the robot. Based
in rotational equation of motion, see equation 3, and
considering null friction values (B
w
e B
cw
), we get:
Γ(t) = J
dW (t)
dt
(19)
The torque Γ(t) and the applied force f
m
(t) are
Γ(t) = f
m
(t)r
m
(20)
f
m
(t) = m
o
g (21)
where g is the acceleration of gravity (≈
9.8[m/s
2
]), m
o
is the mass and r
m
is the radius
disc(0.25[m]).
Four experiments had been made to identify the
value of J. The experiments 1, 2 and 3 were per-
formed with an object with mass equal 0.510 Kg, and
the experiment 4 with a object with mass equal 1 Kg.
Our objective was to verify the repeatability of the ex-
periments.
The figure 9(a) shows the angular position (θ(t))
curve for the first experiment. The angular velocities
(W (t)) were calculated using the derivative of the an-
gular position. The figure 9(b) shows the angular ve-
locity and the best fitting line to the angular velocity,
calculated by least-squares line method, that give us
the value of the angular accelerations.
The table 4 shows the torque values(Γ), angu-
lar accelerations(
dW (t)
dt
) and inertia moments(J) ob-
tained by experiments. The inertia moments were
similarly in all experiments.
ICINCO 2006 - ROBOTICS AND AUTOMATION
568

Table 4: Estimated inertia moments.
Exp. 1 Exp. 2 Exp. 3 Exp. 4
Γ(N.m) 1.2495 1.2495 1.2495 2.4500
dW (t)
dt
(rad/s
2
)
0.9126 0.8942 0.8947 1.7512
J(kg.m
2
) 1.3691 1.3974 1.3965 1.3990
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
1
2
3
4
5
6
7
8
9
10
11
time[sec]
theta [rad]
(a) θ(t)(rad)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
time[sec]
W [rad/s]
(b) W(t)(rad/s)
Figure 9: First experiment.
3.4 Comparing Methods
The identified parameters are presented in tables 5
and 6. We can see a acceptable difference between
the estimated values, take into account that the exper-
iments had been made in hard conditions. For exam-
ple, the measured values of currents and velocities
have a considerable noise and any irregularity in the
floor can cause alterations in robot parameters. In the
model robot was used the mean of estimated parame-
ters.
Table 5: Estimated frictions.
Frictions Viscous Coulomb
B
v
B
vn
B
w
C
v
C
vn
C
w
Method 1 3.45 2.90 0.73 28.55 28.46 5.12
Method 2 4.01 3.77 - 30.35 30.76 -
Mean 3.73 3.34 0.73 29.45 29.61 5.12
4 SIMULATION AND REAL
RESULTS
In this section the model simulation with the es-
timated parameters is presented. The simula-
tion environment was the Matlab/Simulink soft-
ware(Mathworks, 2000). Three simulations had been
made (see Figs.10, 11 and 12), using the following
reference velocities:
1. V = 1[m/s], V
n
= 0[m/s], W = 0[ rad/s];
2. V = 0[m/s], V
n
= 1[m/s], W = 0[ rad/s];
3. V = 0[m/s], V
n
= 0[m/s], W = 1[ rad/s].
The Figs. 10(a), 11(a) and 12(a) show the results of
the simulation and the real velocities of the robot. The
Table 6: Estimated inertia moments.
Inertia Moments
Methods 1+2 1.358
Method 3 (mean) 1.390
Mean 1.374
simulation results are very similar to the real ones, in
the transitory and the steady state too.
In Figs. 10(b), 10(c), 11(b) and 11(c) we can see
some non-linearities of the robot, due to PWM satu-
ration, shown in Figs. 10(d), 10(e), 11(d) and 11(e).
The simulated currents had a good approximation to
the real ones, because the model could find even some
non-linearities of the system.
In third simulation(see Fig.12), the motors do not
saturate easily, because there are 4 motors simultane-
ously applying force. In this way, the transitory state
become much more fast.
0 0.5 1 1.5
0
0.2
0.4
0.6
0.8
1
Time[sec]
V[m/s]
Real
Simulated
(a) Real and simulated V (m/s).
0 0.5 1 1.5
−6
−5
−4
−3
−2
−1
0
Motor 2
Time[seg]
i2 [A]
Real
Simulated
(b) Current i2(A)
0 0.5 1 1.5
0
1
2
3
4
5
6
Motor 4
Time[sec]
i4 [A]
Real
Simulated
(c) Current i4(A)
0 0.5 1 1.5
−300
−250
−200
−150
−100
−50
0
PWM motor 2
Time[seg]
Duty cycle[0..255]
Real
Simulado
(d) PWM motor 2
0 0.5 1 1.5
0
50
100
150
200
250
300
PWM motor 4
Time[sec]
Duty cycle[0..255]
Real
Simulado
(e) PWM motor 4
Figure 10: Velocity V = 1, simulation 1.
5 CONCLUSION
In this paper an experimental identification of the dy-
namic parameters of an omni-directional mobile robot
has been developed. Three methods of the parameters
DYNAMIC PARAMETERS IDENTIFICATION OF AN OMNI-DIRECTIONAL MOBILE ROBOT
569

0 0.5 1 1.5
0
0.2
0.4
0.6
0.8
1
Vn[m/s]
Real
Simulated
Time[sec]
(a) Real and simulated V
n
(m/s).
0 0.5 1 1.5
0
1
2
3
4
5
6
Motor 1
Time[sec]
i1 [A]
Real
Simulated
(b) Current i1(A)
0 0.5 1 1.5
−6
−5
−4
−3
−2
−1
0
Motor 3
Time[sec]
i3 [A]
Real
Simulated
(c) Current i3(A)
0 0.5 1 1.5
0
50
100
150
200
250
300
PWM motor 1
Time[sec]
Duty cycle[0..255]
Real
Simulado
(d) PWM motor 1
0 0.5 1 1.5
−300
−250
−200
−150
−100
−50
0
PWM motor 3
Time[sec]
Duty cycle[0..255]
Real
Simulado
(e) PWM motor 3
Figure 11: Velocity V
n
= 1, simulation 2.
identification that even can be used in dynamic mo-
delling were described. A robot model that could find
the non-linear elements is very important to design
of controllers and trajectories, mainly in application
where critical trajectories must be executed at higher
velocity, for example in robotic soccer. In the near fu-
ture, we will use the robot model to design controllers.
REFERENCES
Franklin, G. F., Powell, J., and Workman, M. (1997). Digi-
tal control of dynamic systems. Addison Weley Long-
man, Inc, 3 edition.
Liu, Y., Wu, X., Zhu, J. J., and Lew, J. (2003). Omni-
directional mobile robot controller design by trajec-
tory linearization. Proceedings of the American Con-
trol Conference, 4:3423 – 3428.
Mathworks, T. (2000). MATLAB Users’ Guide.
Watanabe, K. (1998). Control of ominidirectional mobile
robot. 2nd Int. Conf. on Knowledge-Based Intelligent
Electronic Systems.
0 0.5 1 1.5
0
0.2
0.4
0.6
0.8
1
Time[sec]
W[rad/s]
Real
Simulated
(a) Real and simulated W(rad/s).
0 0.5 1 1.5
0
0.5
1
1.5
2
2.5
Motor 1
Time[sec]
i1[A]
Real
Simulated
(b) Current i1(A)
0 0.5 1 1.5
0
0.5
1
1.5
2
2.5
Motor 3
Time[sec]
i3 [A]
Real
Simulated
(c) Current i3(A)
0 0.5 1 1.5
0
0.5
1
1.5
2
2.5
Motor 2
Time[sec]
i2[A]
Real
Simulated
(d) Current i2(A)
0 0.5 1 1.5
0
0.5
1
1.5
2
2.5
Motor 4
Time[sec]
i4 [A]
Real
Simulated
(e) Current i4(A)
0 0.5 1 1.5
0
50
100
150
200
250
300
PWM motor 1
Time[sec]
Duty cycle[0..255]
Real
Simulated
(f) PWM motor 1
0 0.5 1 1.5
0
50
100
150
200
250
300
PWM motor 3
Time[sec]
Duty cycle[0..255]
Real
Simulated
(g) PWM motor 3
0 0.5 1 1.5
0
50
100
150
200
250
300
PWM motor 2
Time[seg]
Duty cycle[0..255]
Real
Simulated
(h) PWM motor 2
0 0.5 1 1.5
0
50
100
150
200
250
300
PWM motor 4
Time[sec]
Duty cycle[0..255]
Real
Simulated
(i) PWM motor 4
Figure 12: Velocity W = 1, simulation 3.
ICINCO 2006 - ROBOTICS AND AUTOMATION
570