STUDIES ON VISUAL PERCEPTION
FOR PERCEPTUAL ROBOTICS
Özer Ciftcioglu, Michael S. Bittermann, I. Sevil Sariyildiz
Department of Building Technology, Delft University of Technology, Berlageweg 1, 2628 CR Delft, The Netherlands
Keywords: Visual perception, perception modeling, perception measurement, robotics, genetic search.
Abstract: Studies on human visual perception measurement for perceptual robotics are described. The visual
perception is mathematically modelled as a probabilistic process obtaining and interpreting visual data from
an environment. The measurement involves visual openness perception in virtual reality, which has direct
implications for navigation issues of actual autonomous robotics. The perception is quantified by means of a
mapping function which converts a distance to an elemental perception estimate. The measurement is
carried out with the averaging of the elemental perceptions in real time. This is accomplished by means of
exponential averaging. The mapping function parameters are optimized uniquely by means of genetic
algorithm approach where the data set for model development consists of a number of perception data
samples. These are obtained from individuals who are confronted with a number of scenes and asked for
their perceptual openness statements. Based on this data, a perception model is developed for a virtual robot
where the simulated vision interaction of the robot with the environment is converted to visual openness
estimation through the model output. The model outcome is essential visual information for the navigation
of an autonomous perceptual robot.
1 INTRODUCTION
Robot navigation is one of the major fields of study
in autonomous robotics (Beetz et al., 2001, Wang
and Liu, 2004). As data source for navigation a
number of approaches have been proposed. For
instance video image processing (Florczyk, 2005),
or obtaining distances between robot and its
environment by means of ultrasonic sensors (Oriolio
et al., 1998), infrared (Song and Cho, 2000), or via
3D laser (Surmann et al., 2001). In this work, the
simulated laser approach is considered and
implemented in a virtual reality (VR) environment.
Being peculiar to this specific research, in place of
merely measuring the distances between the robot
and its environment, the robot’s perception about its
environment as to visual openness is considered.
From the architectural design viewpoint, visual
openness is an important concept in architecture and
interior design. Since the shape of a space is
responsible for the perception of an observer, visual
openness is attributed as an inherent quality to the
space. From the robotics viewpoint, visual openness
perception is characteristic information about the
environment and therefore can be used for the
human-like navigation of an autonomous perceptual
robot.
In the present work, a virtual robot is used as a
representative of a human, who moves through a
space making continuous visual openness
assessment about the environment for building
technological design purposes. This assessment also
can form a base of navigation information for path
planning to make the robot autonomous with human-
like visual openness assessments along the path it
determines and moves.
2 PERCEPTION MODEL
DEVELOPMENT
2.1 Theoretical Considerations
The subject matter of this work is visual openness
perception which has essential implications on
general design process as well as robot movement.
The visual openness perception is obtained from
visual perception data, which are derived from the
distances between observer and environment. That
352
Ciftcioglu Ö., Bittermann M. and Sariyildiz I. (2006).
STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 352-359
DOI: 10.5220/0001221603520359
Copyright
c
 SciTePress

is, the visual openness of a space is perceived in
mind with the association of the distances. This
association is represented in this work by means of a
sigmoid function.
The variation of sigmoid with the independent
variable is shown in figure 1. The sigmoid function
is a special function which is also used to represent
biological processes. One important application is
found in the paradigm of artificial neural networks,
where sigmoid plays the essential role in modeling
the non-linearity of a biological neuron.
0 2 4 6 8 10
0
0.5
1
sigmoid function
x
f(x)
Figure 1: Sigmoid function
)]exp(/[)(
o
xx11xf −+=
which
represents non-linearity in brain processes.
The characteristic behavior of the function is its
saturation at the extremities and its approximately
linear behavior in the middle range. Since such
functionality can be surmised to occur in each
neuron in the brain, the modeling of visual openness
perception by such a function is a prominent choice
among other options potentially available.
Qualitatively, by means of the sigmoid function the
perception of the visual openness at small distances
is considered to be small with no significant change
in this fuzzy range. A similar behavior is observed at
the other extreme considering that the visual
openness perception does not deviate significantly as
the distance approaches to extreme values. At the
middle range, the visual openness perception is
highly dependent on the distance, as one should
expect. These qualitative observations about the
perception model are similar to many other
biological processes of a human and they conform to
the common visual openness perception experience
of a human, in general.
Another interesting feature of sigmoid is that it is
used to measure the perception quantitatively in the
range between 0 and 1. This is a very significant
feature especially while the robot is experiencing
and evaluating the visual openness of a space as a
fuzzy statement. Such statements can be statistically
analyzed to establish the visual openness perception
model parameters.
For the visual openness perception measurement
we use the laser option, where the length of each
visual ray between human eye and an object in the
environment is represented by a laser ray spanning
the ray source and the object. The distance is used to
measure the visual openness perception. In this case,
the laser source provides rays not in scanning mode
but as a random source of rays with certain statistical
properties, which are derived below. A number of
rays are traced in this way and consequently the
same amount of perception data is obtained. That is
for each particular ray an elemental visual openness
perception is obtained via a sigmoid function. By
averaging these individual mapping function
outcomes, the visual openness perception, as a
measurement outcome, is obtained. The averaging is
performed on a sample by sample basis so that the
time-dependent measurement can be accomplished
in real-time. If the time constant of the exponential
averaging is kept sufficiently small then the
measurement outcome can be used for robot
navigation due to minimal latency of the
measurement. In the case of a moving robot, it
experiences human-like interaction with the
environment.
For the visual openness perception model
development and the analysis of the role of the
sigmoid function, which maps the physical distance
to visual openness perception, we start with the
basics of the perception process with a simple yet
fundamental geometry. This is shown in figure 2.
P
x
l
o
z
0
z
Figure 2: The geometry of visual perception from a top
view where P represents the position of eye, looking at a
vertical plane with a distance l
o
to the eye; f
z
(z) is the
probability density function of the perception.
In figure 2, the observer is facing and looking at a
vertical plane from the point denoted by P. By
means of looking action the observer pays visual
attention equally to all directions within the scope of
sight. That is, at the first instance, the observer
visually experiences all regions of the plane without
any preference for one region over another. Each
location on the plane has its own distance within the
STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
353

observer’s scope of sight which is represented as a
cone. The cone has a solid angle denoted by
θ . The
distance of a point on the plane and the observer is
denoted by x and the distance between the observer
and the plane is denoted by l
o
. Since the visual
perception is determined via the associated
distances, it is straightforward to proceed to express
the distance of visual perception in terms of
θ . From
figure 2, this is given by
)cos(θ
=
o
l
x
(1)
Since we consider the observer pays visual attention
equally for all directions within the scope of sight in
the first instance, the probability density function
(pdf), which is associated with the directions, is
uniformly distributed. Consequently, assuming the
scope of sight is defined by the angle
θ = π /4, the pdf
f
θ
is given by
2
1
f
/π
=
θ
(2)
Since
θ is a random variable, the distance x in (1) is
also a random variable. The pdf f
x
(x) of this random
variable is computed as follows.
Theorem on the function of random variable: To
find f
x
(x) for a given x we solve the equation
x= g(
θ ) (3)
for
θ in terms of x. If θ
1
, θ
2
,…., θ
n
, .. are all its
real roots, x=g(
θ
1
) = g( θ
2
) =……= g( θ
n
) = ….
Then
..
|)('|
)(
...
|)('|
)(
...
|)('|
)(
)( +
θ
θ
++
θ
θ
++
θ
θ
=
θθ
n
nx
2
2
1
1
x
g
f
g
f
g
f
xf
(4)
Clearly, the numbers
θ
1
, θ
2
,…., θ
n
, .. depend on x.
If, for a certain x, the equation x= g(
θ ) has no real
roots, then f
x
(x)=0.
According the theorem above,
)(cos
)sin(
)('
2
θ
θ
θ
θ
o
l
d
dx
g ==
(5)
Between θ= -π/4 and θ= +π/4,
)cos(
)(
θ
=θ
o
l
g
(6)
has two roots, which are equal and given by
)arccos(
,
x
l
o
21
=θ
(7)
Using (7) in (5), we obtain
o
2
o
2
l
lxx
g
−
=θ)('
(8)
Substituting (2), (7) and (8) into (4), we obtain
22
4
)(
o
o
x
lxx
l
xf
−
=
π
(9)
for the interval
)4/cos( π
o
o
l
xl ≤≤
. For this
interval, the integration below becomes
1
4
)(
2
22
2
=
−
=
∫∫
o
o
o
o
l
l
o
o
l
l
x
lxx
dx
ldxxf
π
(10)
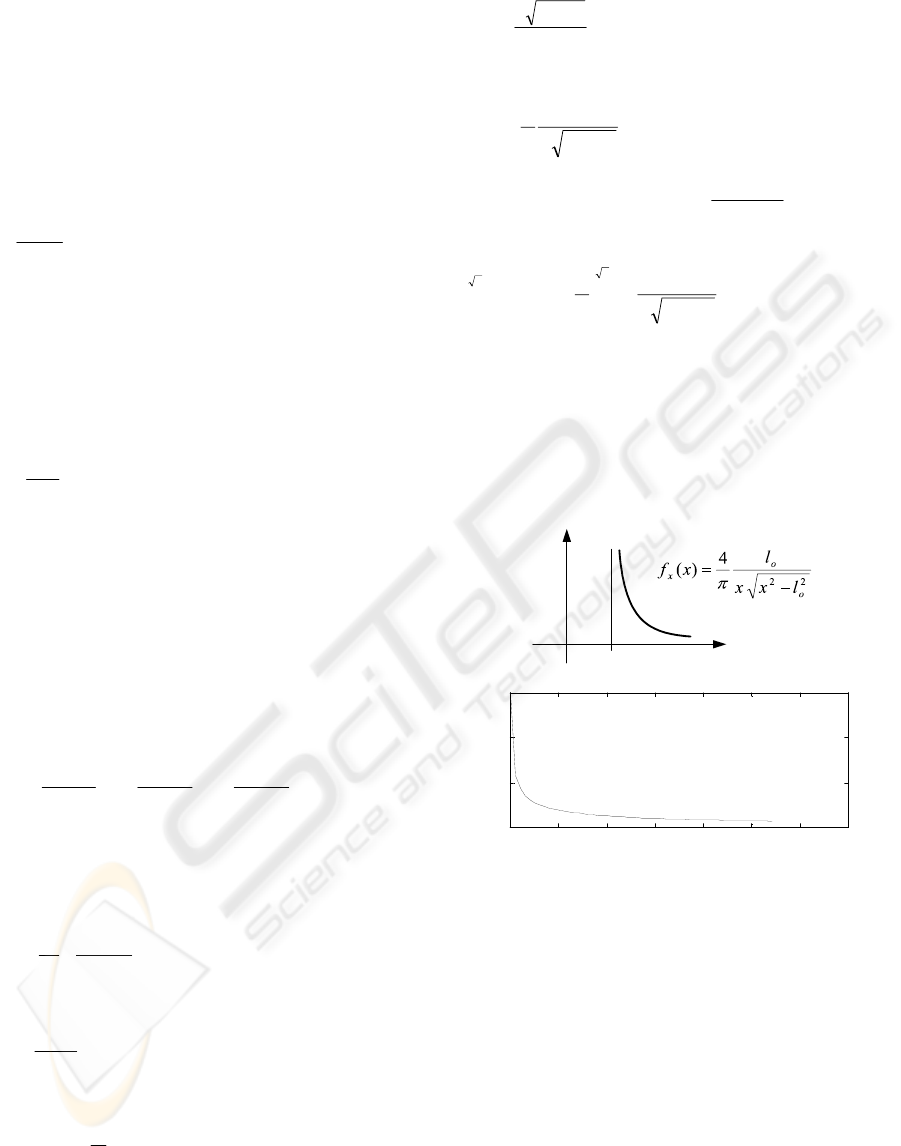
as it should be as a pdf. The sketch of f
x
(x) vs x is
given in figure 3 (upper) and its variation for l
o
=1 is
also given in the same figure (lower). In place of a
plane geometry, for a circular geometry, the pdf f
x
(x)
in (9) takes a uniform distribution, as it is shown in
the Appendix.
f
x
(x)
0
x
l
0
1 1.05 1.1 1.15 1.2 1.25 1.3 1.35
0
10
20
30
probability density of visual perception
x
f(x)
Figure 3: Variation of the probability density of random
variable x representing the distance between eye and a
location on a plane shown in figure 1. The upper plot is a
sketch; the lower one is a computed plot with l
o
=1.
It is interesting to note that for the plane
geometry in figure 2, the visual perception is sharply
concentrated close to x = l
o
or θ ≅ 0, that is in
perpendicular direction to the plane. This striking
result is in conformity with the common human
experience as to visual perception. Namely, for this
geometry the visual perception is strongest along the
axis of the cone of sight relative to the side
directions. To see this in mathematical terms, we
extend our calculations to derive the pdf along the z
direction in figure 2. In this case, proceeding in the
same way before, we write
ICINCO 2006 - ROBOTICS AND AUTOMATION
354

)()(
)(
θθ
θ
tglgz
l
z
tg
o
o
==
=
(11)
)1()((
)(cos
)('
2
2
2
2
o
oo
o
l
z
ltgil
l
d
dz
g +=+===
θ
θθ
θ
(12)
)/(
1 o
lzarctg= θ
)(
|)('|
)(
)(
22
1
1
zl
l
g
f
zf
o
o
z
+
==
π
θ
θ
θ
(13)
for the interval
∞≤≤∞−
z
. For this interval,
the integration below becomes
1)(
22
=
+
=
∫∫
+∞
∞−
∞+
∞−
o
o
z
lz
dz
l
dzzf
π
as it should be. The variation of f
z
(z) is shown in
figure 2. This result clearly explains the relative
importance of the front view as compared to side
views in human visual perception. In the visual
perception measurement system, f
z
(z) is taken close
to a Gaussian function, for computational
convenience. The implication of this approximation
to the exact f
x
(x) given by (9) is presented below.
From figure 2, we can write
22
o
2
zlx +=
(14)
where
2
2
2
1
2
2
1
)(
z
z
ezf
σ
πσ
−
=
(15)
From (14), we write
2
o
22
lxz −=
, so that
2
o
2
21
lxz −±=
,
(16)
22
)( zlzg
o
+=
(17)
1
z
l
1
dz
dg
zg
2
o
+
⎟
⎠
⎞
⎜
⎝
⎛
==)('
(18)
Substituting z
1,2
from (16) into (18) yields
1
lx
l
1
zg
2
o
2
2
o
21
+
−
=)('
,
(19)
From the function of a random variable theorem
..
|)('|
)(
...
|)('|
)(
...
|)('|
)(
)( +++++=
n
nz
2
2z
1
1z
x
zg
zf
zg
zf
zg
zf
xf
(20)
|)('|
)(
|)('|
)(
)(
2
2
1
1
zg
zf
zg
zf
xf
zz
x
+=
we obtain
)(
)(
2
o
2
lx
2
1
2
o
2
x
e
lx
x2
xf
−−
−
π
=
(21)
which is the modified form of exact f
x
(x) in (9) due
to approximation of f
z
(z) in (13) by a Gaussian. Both
pdfs of f
z
(z) given by (9) and given by (21) are
shown together for comparison in figure 4, where
the difference appears to be not significant for this
research.
1 1.5 2 2.5 3 3.5 4 4.5 5
0
2
4
6
8
10
x
f(x)
p
dfs
Figure 4: The visual perception pdf f
x
(x) and
approximation to it (lower) due to Gaussian pdf f
z
(z) in
figure 2.
The result of the relative importance of the front
view as compared to side views in human visual
perception can be explained easily as sketched in
figure 5.
P
l
o
1
2
0
z
1
2
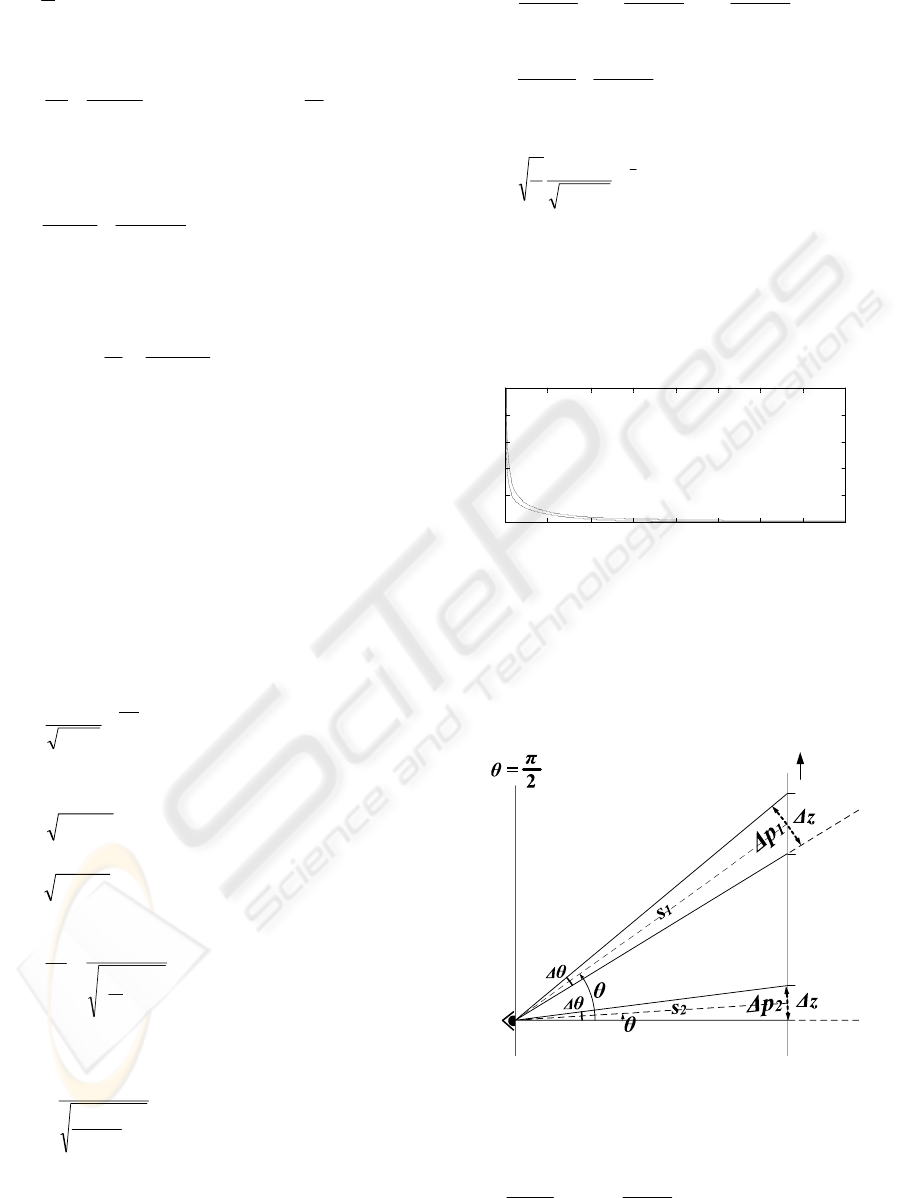
Figure 5: Sketch explaining the relative importance of the
viewing direction for visual perception.
In figure 5,
θ
θ
θ
θ
cos
,
cos
2
2
1
1
s
z
s
z
Δ
≅Δ
Δ
≅Δ
STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
355

2
2
1
1
cos
;
cos θθ
oo
l
s
l
s ==
, so that
2
2
2
1
2
1
cos
,
cos θ
θ
θ
θ
oo
l
z
l
z
Δ
≅Δ
Δ
≅Δ
Noting that for
θ =0, we obtain
2
2
12
cos
,
θ
θ
θ
o
o
l
zlz
Δ
≅ΔΔ≅Δ
(22)
Since Δz
2
<Δz
1
, this clearly shows that the visual
resolution is higher for the case with
θ
2
relative to
the case with
θ
1
. This implies that one gets more
visual details at the origin as the visual resolution is
higher there and consequently the general shape of
pdf f
z
(z) exhibits a maximum for θ
2
there, which can
be seen in figure 2.
The next step is to move from visual perception
to visual openness perception via the sigmoid
function. In this case we aim at to find the pdf of the
sigmoid function output when the independent
variable has the pdf of visual perception given by
(10). In this case the theorem on the function of
random variable can be written as
...
|)('|
)(
...
|)('|
)(
...
|)('|
)(
)(
2
2
1
1
+++++=
n
nxxx
y
xg
xf
xg
xf
xg
xf
yf
(23)
where f
x
(x) is given by (7) and g(x) is the sigmoid
function given by
)(
o
xx
e1
1
y
−−
+
=
(24)
We use the theorem on the function of random
variable given by (23), to obtain the pdf of the visual
openness perception. For that matter, first we
compute the derivative of g(x) with respect to x
where
)(
)(
o
xx
e1
1
xg
−−
+
=
(25)
and the derivative is found to be
2
xx
xx
o
o
e1
e
xg
][
)('
)(
)(
−−
−
+
=
(26)
From (25), the root of the equation is obtained as
o1
x
y1
y
x +
⎥
⎦
⎤
⎢
⎣
⎡
−
= ln
(27)
Substitution of (27) into (9) gives
2
2
1
1
ln]
1
ln[
4
)(
)()(
ooo
x
xx
lx
y
y
x
y
y
yf
yfxf
−
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
=
π
(28)
2
1
yyxg −=)('
(29)
Now, substitution of (28) and (29) into (23), yields
2
2
2
1
ln]
1
ln)[(
4
)(
ooo
y
lx
y
y
x
y
y
yy
yf
−
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
π
(30)
for the interval corresponding to
θ =± π/2, in figure 2
oo
oo
xl
xl
e
x
e
−−
−−
+
≤≤
+
2
(
1
1
)1
1
This is the pdf of the visual openness perception.
Variation of this function is shown in figure 6, for
x
o
=1 and l
o
=1. For this case 0.5000≤ x≤0.6021.
0.5 0.52 0.54 0.56 0.58 0.6 0.62
0
50
100
150
200
pdf of visual openness perception
y
f(y)
Figure 6: Plot of probability density function of random
variable representing the output of the sigmoid function as
visual openness perception measurement outcome.
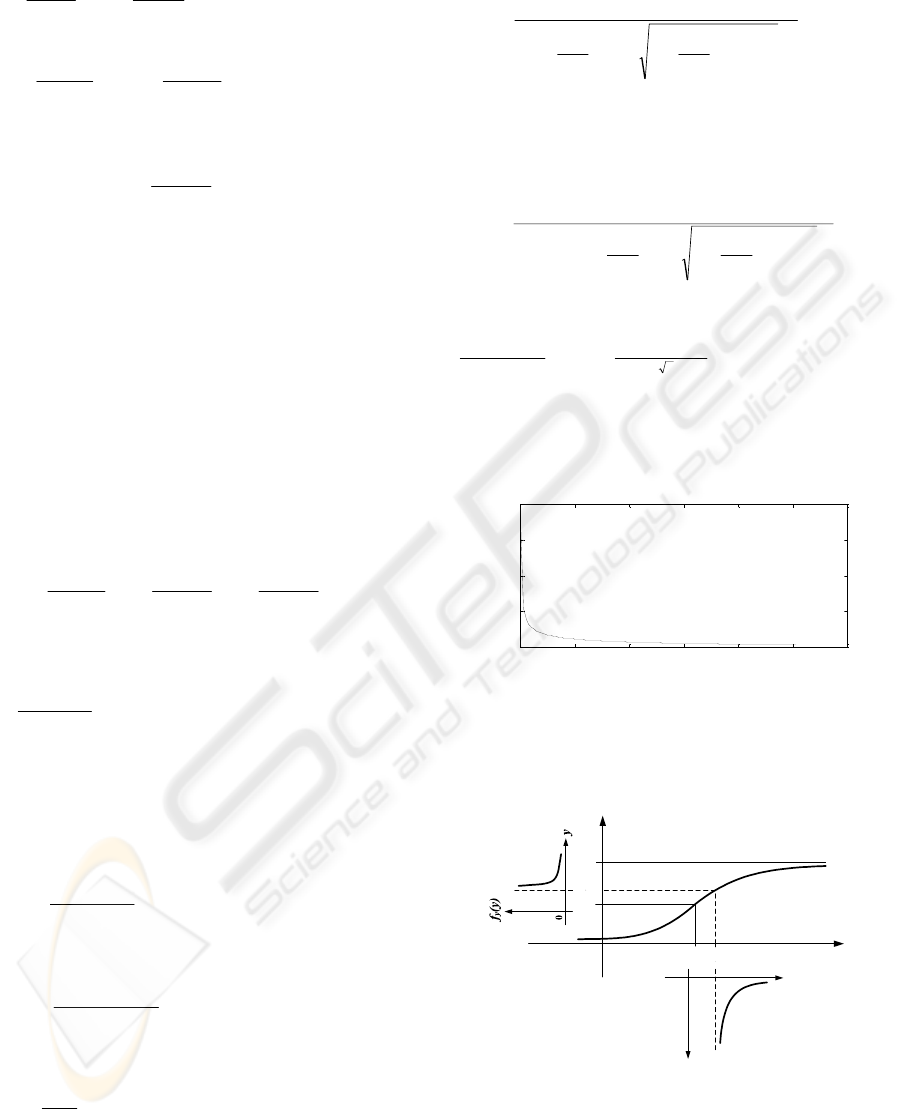
The f
x
(x) and f
y
(y) are depicted together in figure 7 to
summarize the probabilistic computations above.
1
0.5
0
y=g(x)
f
x
(x)
y
x
0
x=l
0
0
x
x
Figure 7: The sketch of both probability density functions
of random variables x and y at the sigmoid input and
output respectively.
From figure 7, it is seen that, the visual openness
perception is also strongly concentrated at the
distance x=l
o
, which is in the direction perpendicular
ICINCO 2006 - ROBOTICS AND AUTOMATION
356

to the plane, along the axis of the cone in figure 2.
This means both visual perception and visual
openness perception have similar properties, namely
exhibiting maximum concentration along the axis of
the visual sight cone. This is what one commonly
experiences during the perception of the
environment.
To simplify the f
y
(y) in (30), we can consider the
case where g(x) is approximately linear so that
function of a random variable y=f(x) is given by
y=a x + b (31)
In this case the equation y=ax+b has a single
solution
a
by
x
−
=
(32)
for every y. Since g’(x)=a, we conclude from (23)
that the density of y is given by
⎟
⎠
⎞
⎜
⎝
⎛
−
=
a
by
f
a
1
yf
xy
||
)(
(33)
and therefore
2
2
14
||
1
)(
o
y
l
a
by
a
by
a
yf
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=
π
(34)
Since the sigmoid function can be approximated by
three linear functions as local approximations, it is
easy to conclude that, the general formulation of
f
y
(y) as to visual openness perception remains the
same having latent dependency to the parameters x
o
and l
o
, via the parameters a and b in (31), where x
o
and l
o
are the shift of sigmoid and the distance of the
observer to the plane, respectively.
2.2 Determination of the Model
Parameters
For the determination of the parameters in the
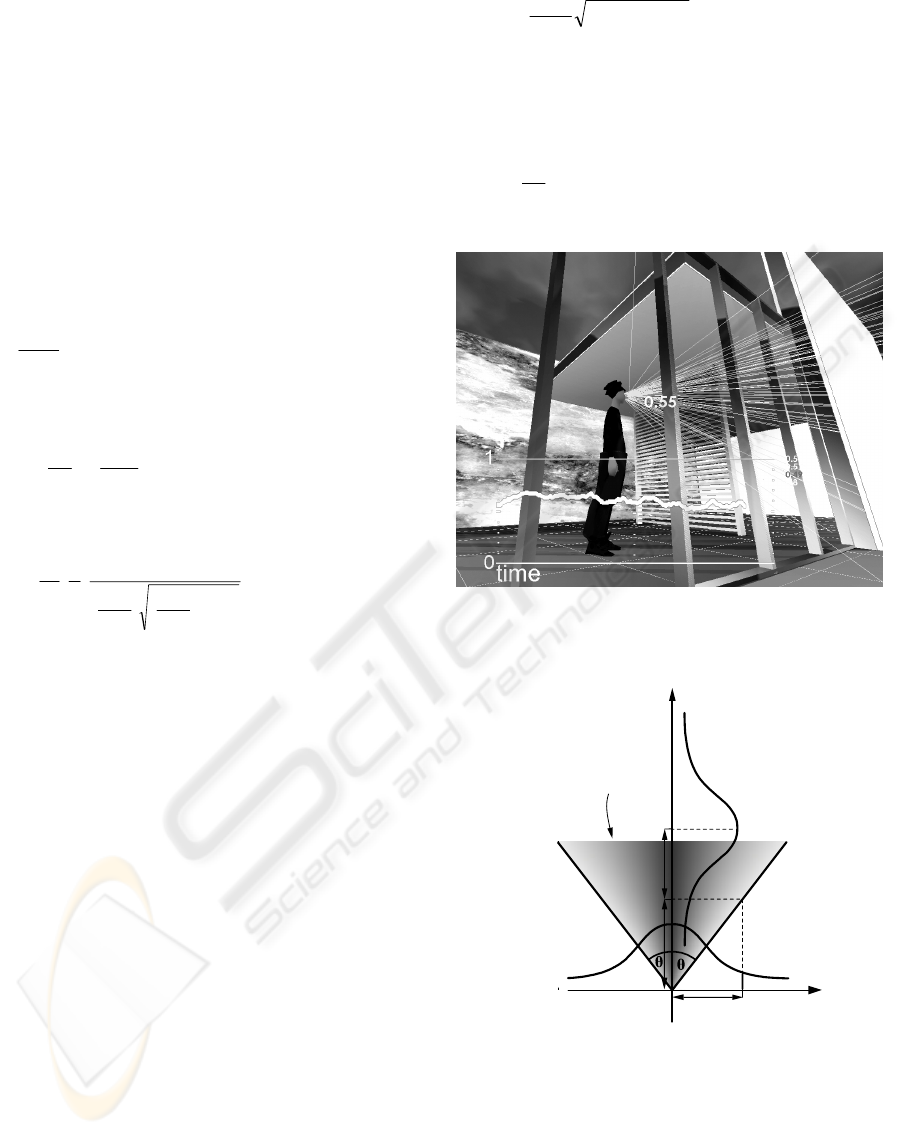
human visual openness perception model, a vision
robot in virtual reality is employed as shown in
figure 8. The robot senses its spatial environment by
sending rays from its eyes and measuring each
length as they hit shapes, which are around the
robot. The rays are sent in random directions with a
Gaussian pdf as an approximation to f
z
(z) given by
(13). Formation of Gaussian vision in forward
direction with a cone of angle 2
θ is sketched in
figure 9 where z is the forward direction in the z-x
plane. In figure 9, m
z
is given by (Ciftcioglu et al.,
2006)
)2ln(
)(
1
1(
22
a
tg
m
z
πσ
θ
−+=
(35)
where m
z
is the mean in z-direction and σ= σ
x
= σ
z
is
the variance of both Gaussians given by f
x
(x) and
f
z
(z). Note that to have a solution in (35) σ and a
must have the condition
π
σ
2
1
22
<a
(36)
to obtain a real value for m
z
.
Figure 8: Virtual perceptual robot viewing environment
for visual perception determination. The real-time plot of
the perception measurement outcome is indicated.
cone of vision
f
x
(x)
f
z
(z)
m
x
=0
x
p
s
x
m
z
s
x
s
z
z
Figure 9: Formation of Gaussian vision in forward
direction with a cone of angle 2
θ . z is forward direction of
the robot in the z-x plane.
The lengths of the rays are converted to virtual
openness perception data samples via the sigmoid
function, which remains the same throughout the
computer experiments. A number of perception data
samples are averaged to obtain the degree of visual
openness perception of the environment. For this
STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
357

purpose exponential averaging is used. In
exponential averaging previously obtained average
information is incorporated into the computation of
the current average. By means of this, the average,
which is the measurement outcome, is updated in
real-time in a computationally efficient and effective
way. Greater values for the time constant in
exponential averaging yield more accurate
measurement outcomes, since more data is used to
identify the perception. As a trade off, the time-
duration it takes to establish the outcome increases.
At the same time the value of the exponentially
averaging time-constant determines the accuracy of
the measurement outcome in terms of reflecting
details of the geometric shape of the perceived space
via the pdf of the outcome. The higher the value
used for the moving exponential averaging window
is, the more accurately shape details of the
environment are reflected in the measurement
outcome.
Different persons often attribute different
degrees of visual openness to the same spatial
situation. This indicates that their perceptions are
different. To model the perception of individuals as
well as to find a standard, jointly valid human
perception model is an interesting endeavour from a
number of perspectives. For example, in design,
requirements for perceptual spatial qualities are
generally expressed based on subjective perception.
Assessment of requirement satisfaction is a
necessary component in the search for optimal
spatial shapes, which is an essential activity in
architecture and interior design. Another
implementation is for robot navigation where the
robot uses the common perceptual information about
its environment for path planning with humanoid
behaviour.
2.2.1 Model Identification by Means of
Genetic Algorithm
Systematic finding of the appropriate parameter
settings of the perception model is essentially an
optimality search. Goal of the determination of
appropriate model parameters is to maximize the
match between modeled perception and human
perception. For this purpose a number of perception
outcomes are calculated for a selection of spatial
scenes, which are also subject to perception
assessment by a number of test persons.
Since the visual field is modeled by the random
sight lines, the parametric expression of scene
cannot be given. That is, although the statistical
properties can be analyzed by probabilistic
computation methods using the probability density
functions involved, these results cannot be
incorporated analytically with the scene for
perception assessment. This is due to the visual
perception model which receives discrete non-
stationary random inputs as granulated elemental
perceptions. The stochastic non-stationarity is due to
the heterogeneity of the environment that it yields
different pdf in the visual perception. In order to be
able to handle this non-stationarity imposed on the
random inputs, a randomized search method is used,
where the discrete nature of the optimization task is
also conveniently taken care of. This method is
genetic algorithm based optimization, which is
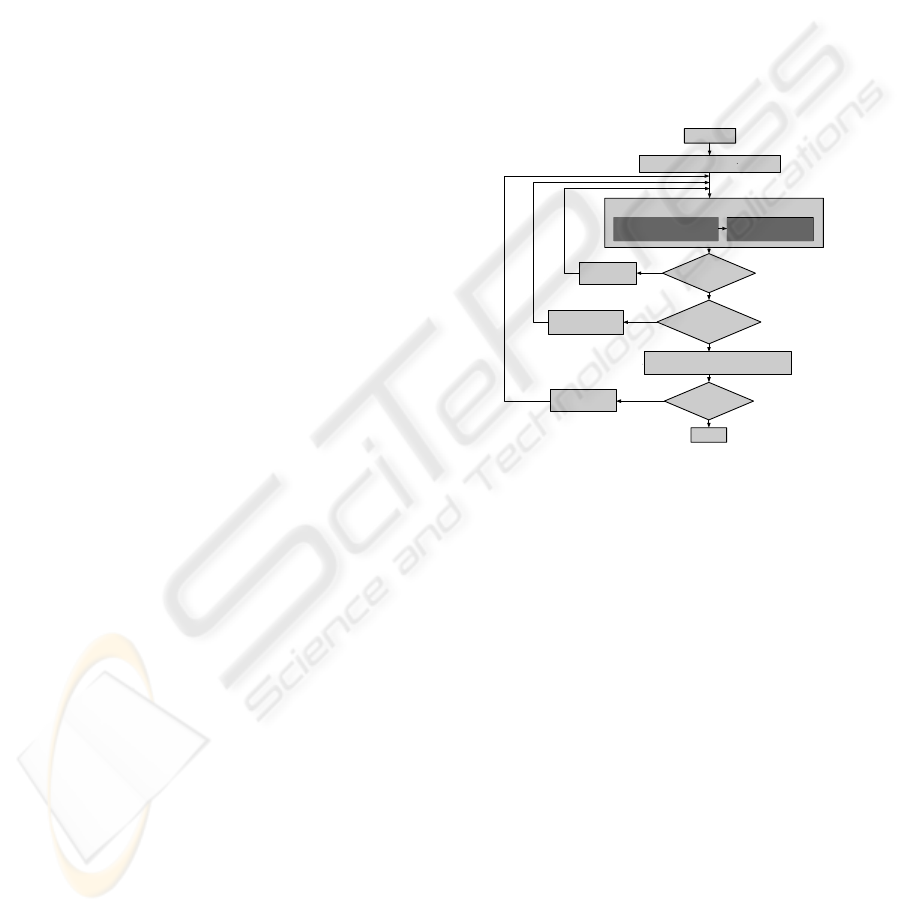
employed as shown in Figure 10.
GENETIC OPERATIONS
INITIALIZE POPULATION
EVALUATE FITNESS OF MODEL
assess scene with model
using current setting
compare result with
given assessment
END
are all scenes
considered?
are all
possible solutions
considered?
is end criterion
fulfilled?
START
no
no
no
yes
yes
yes
take the next
scene
take the next
possible solution
apply globally
best solution
Figure 10: Schematic description of the visual perception
model-identification process by means of genetic
optimization.
The dataset used to assess the fitness of
chromosomes during the genetic evolution are
statements of human experimenters regarding their
subjective assessment of the visual openness for
each scene on a scale from zero to ten. In case of
visual openness, ten signifies maximum and zero
minimum visual openness. These statements are then
normalized to values between 0 and 1 matching the
range of the sigmoid function used in the
measurement model.
It is noteworthy to stress that genetic optimization
has prominent features for this particular
measurement system to be able to deal with the non-
stationary probabilistic nature of the data samples
subject to process and to establish optimality as to
actual calibration of the system. By doing so
adaptivity is included in the optimization process for
other executions involving any additional aspects
like spatial complexity, for instance. This can be
accomplished conveniently via some modification
on the fitting function of the algorithm. After the
ICINCO 2006 - ROBOTICS AND AUTOMATION
358

genetic evolution the best solutions can be
considered as the models of visual openness
perception for the test persons.
3 CONCLUSION
The visual perception is investigated and perception
of visual openness measurement is presented. The
measurement system is established through an
associated perception model which is based on
probabilistic considerations. The visual openness is
measured by means of this probabilistic model. This
is most appropriate since the human vision system
deals with the natural images using their statistical
properties rather than dealing with each piece of
image information in order to be able to cope with
the complexity of information. For changing scenes,
the statistical properties of visual information
become non-stationary and the visual process
becomes a stochastic process, which is peculiar to
this specific research on perception. By means of the
model, the characteristic aspects of visual perception
are substantiated providing ample insight into the
complex visual process.
For the model formation, the method of genetic
algorithm is uniquely employed due to the non-
stationary nature of the case subject to optimization.
The visual openness perception is exercised by a
virtual robot having human-like visual perception in
a virtual environment with a definitive trajectory, to
provide openness assessments as measurement
outcomes. Among other applications, such a robot is
intended for emulation of human perception
providing input for enhanced architectural design.
Another important application of common interest is
autonomous robotics where the robot moves in an
environment without collision by having real-time
visual openness perception information during the
move without any predefined trajectory. This
approach is rather unique as to the novelty of the
visual openness perception concept presented here
for robotics while a prototype is implemented in
virtual reality.
REFERENCES
Beetz, M. et al., 2001. Integrated, plan-based control of
autonomous robots in Human Environments. In IEEE
Intelligent Systems. September-October, pp. 2-11.
Ciftcioglu, Ö., Bittermann, M.S. and Sariyildiz, I.S., 2006.
Application of a visual perception model in virtual
reality. In Proc. APGV06, Symposium on Applied
Perception in Graphics and Visualization, ACM
SIGGRAP. July 28-30, Boston, USA.
Florczyk, S., 2005. Robot Vision: Video-based Indoor
Exploration with Autonomous and Mobile Robot,
Wiley.
Oriolio, G., Ulivi, G. and Vendittelli, M., 1998. Real-time
map building and navigation for autonomous robots in
unknown environments. In IEEE Trans. Syst., Man,
Cybern. – Part B: Cybernetics. 28:3, pp. 316-333.
Song, G.B., Cho, S.B., 2000. Combining incrementally
evolved neural networks based on cellular automata
for complex adaptive behaviours. ECNN2000, IEEE
Symposium on Combinations of Evolutionary
Computation and Neural Networks. May 11-13, San
Antonio, TX, USA, pp. 121-129.
Surmann, H., Lingemann, K., Nüchter, A. and Hertzberg,
J., 2001. A 3D laser range finder for autonomous
mobile robots. In Proc. 32nd Intl. Symp. on Robotics
(ISR2001). April 19-21, Seoul, Korea, pp. 153-158.
Wang, M., Liu, J. N. K., 2004. On line path searching for
autonomous robot navigation. In Proc. IEEE Robotics,
Autom. and Mechatronics, Singapore, December 1-2,
pp. 746-751.
APPENDIX
In the case of circular geometry, the pdf of the visual
perception becomes uniform as one intuitively
concludes. Referring to figure 2, this is shown
mathematically as follows. In circular geometry, the
random variable connected to θ is ω where
)2//(1)( πθ
θ
=f
θ
θ
ω
o
lg
=
=
)(
(A1)
o
l
d
dg
g ==
θ
θ
θ
)(
)('
(A2)
Using the theorem on the function of random
variable, given by (4) in the text, we write
|)('|
)(
)(
1
1
θ
θ
ω
θ
ω
g
f
f =
(A3)
The root of (A1) is given by
o
l
ω
θ =
1
, which gives
o
l
f
π
ω
ω
2
)( =
(A4)
as uniform pdf of visual perception, which satisfies
1
2
)(
4/
4/
4/
4/
∫∫
−−
==
π
π
π
π
ω
π
ωω
o
o
l
l
o
l
l
d
l
df
, as it should be.
STUDIES ON VISUAL PERCEPTION FOR PERCEPTUAL ROBOTICS
359