Content-Adaptive Data Fusion

Paul Bao

, Le Thanh Hai

Information Technology, University of South Florida, USA

School of Computer Engineering

Nanyang Technological University, Singapore

Abstract. We propose a novel image fusion scheme based on independent

component analysis in which image / information is fused aimed at information

maximization. In the scheme, a novel algorithm is presented which, based on

specific fusing images, determines adaptively a specific weight for linear fusion

of images using ICA. The scheme is established on the ICA maximum informa-

tion principles and offers an efficient and adaptive image fusion process with

the robustness under various fusion situations.

1 Introduction

Image fusion is to combine images of an underlying scene captured by multiple

sensors to synthesize a composite image. Different sensors provide different

information about the scene and are effective in different environmental conditions.

The aim of image fusion is to create a fused image which not only is visually

acceptable (figure 2 shows a misaligned face fusion) by the human visual system

(HVS) but also captures maximum amount of the information offerred by the images

generated from different sensors. A TV and IR image fusion system is illustrated in

figure 1.

Fig. 1. TV & IR Image fusion.

2 Image Fusion Schemes

There are a number of approaches to image fusion, most of which are often classified

into pixel-based or feature based-approaches.

The first and simplest image fusion method is the fusion-by-averaging in which the

fused i

mage is synthesized by averaging corresponding pixels of the sensors images.

Bao P. and Thanh Hai L. (2006).

Content-Adaptive Data Fusion.

In Proceedings of the 2nd International Workshop on Biosignal Processing and Classiﬁcation, pages 23-32

 SciTePress

An advantage of fusion-by-averaging is that it is very computationally effective.

However, averaging works poorly when feature mismatching occurs in fusion im-

ages.

A more popular pixel-based image fusion technique is PCA-based image fusion.

The technique makes use of Principle Component Analysis to decompose the images

into principle components and the PCs are fused together to obtain the PCA fused

image [1-2].

Feature-based image fusion schemes transform images into features such as edges,

and perform fusion in the feature domain. Since different features are important at

different levels of resolution, multi resolution representations of images are normally

generated. And fusion in feature-based techniques is carried out on the multi resolu-

tion pyramid [3].

Fig. 2. An example of misaligning face images.

Fig. 3. Multi scale Decomposition of images.

One of the most popular feature-based schemes is the Laplacian pyramid technique.

In Laplacian pyramid fusion approach, a Gaussian multi-scale pyramid is built for

each image. Then a Laplacian transformation is applied on the Gaussian pyramids to

form Laplacian transformed pyramids of images. Fusion is then applied on Laplacian

pyramids to obtain the fused Laplacian transformed pyramid. By exploiting the per-

fect reconstruction characteristic of Laplacian transform, a fused image can be ob-

tained from the fused pyramid using an inverse Laplacian transform. Over the years,

there has been numerous enhancement added to the original scheme [5]

Toet et al. [4] introduced a contrast based image fusion technique which preserves

local luminance contrast in the sensor images. The technique is based on selection of

image features with maximum contrast rather than maximum magnitude. It is moti-

vated by the fact that the human visual details to a human observer. The pyramid

decomposition used for this technique is related to luminance processing in the early

stages of the human visual system which are sensitive to local luminance contrast.

Fusion is performed using the multi-resolution contrast pyramid.

Wavelet based image fusion techniques, as shown in figure 3, has been a focus

recently. The wavelet transform decomposes the image into baseband at the coarsest

scale and highbands at different scales. The baseband contains the average image

information whereas the various highbands contain directional information due to

spatial orientation. Higher absolute values of wavelet coefficient in the highbands

correspond to salient features such as edges, lines, etc. Li et al. [6] performed fusion

in the wavelet transform using a selection-based rule, while Wilson et al. [7] sug-

gested an extension to wavelet-based fusion using a perceptual-based weighting.

While a number of image fusion approaches has been proposed, the issues of retain-

ing information in the fused images has rarely been touched.

3 ICA Analysis and Image Fusion

Different types of sensors provide different types of information. In some cases, some

information (redundant information) is provided by several types of sensors; in other

cases, some information (complementary information) is produced uniquely by one

type of sensor. In terms of information, the aim of image fusion is twofold: on one

hand it aims to improve reliability (by redundant information), and on the other hand,

it tries to improve capability (by making use of complementary information). Hence,

the problem in image fusion is how to ensure the fused image retains the maximum

information from the original images (figure 4).

Fig. 4. Information in Image fusion.

ICA-based image fusion promises to provide maximum information, in comparisons

to other linear fusion of images (even to its sibling PCA) and offers some interesting

aspects on fused images.

Independent components analysis (ICA) is a mathematical method for separating a

signal into its most probable additive subcomponents supposing the statistical inde-

pendence of the source signals. In real environment, different signals are often statis-

tically independent and ICA techniques can be applied to separate original signals

from a mixture of those signals. ICA is closely related to Blind Source Separation

(BSS) techniques.

ICA is often considered developed from Principal Component Analysis (PCA).

PCA is a way of identifying patterns in data, and expressing the data in such a way as

to highlight their similarities and differences. Since patterns search in high-

dimensional data set is extremely difficult, where the luxury of graphical representa-

tion is not available, PCA is a powerful tool for analyzing data. Figure 5 provides a

graphical representation of a two-dimensional data set and its 2 principle components

Fig. 5. An example of Principal Analysis.

Generally if the data has dimensions, we will have principle components. The

components can be expressed as vectors (eigenvector) in the data space. And PCA

techniques ensure all the eigenvectors are perpendicular.

n n

The principle components will give us the original data solely in terms of the vec-

tors we chose. Our original data set has two coordinates, represented by . It is

possible to express data in terms of any two axes. If these axes are perpendicular, then

the expression is the most efficient. This was why PCA techniques ensure that eigen-

vectors are always perpendicular to each other. Thus, we represent data in the space

of the two eigenvectors instead of .

),( yx

Theoretically there are two (principle) components, but it is possible ignore compo-

nents of lesser significance. In such cases, some information is lost, but if the eigen-

values are small, not much is being lose. The advantage is that the final data set will

have fewer dimensions than the original. In fact, this is the whole concept of PCA

based data compression.

It has been noted that the eigenvector with the highest eigenvalue is the principle

component of the data set. In our example, the eigenvector with the larges eigenvalue

was the one that pointed down the middle of the data. It is the most significant rela-

tionship between the data dimensions.

When all the principal components are retained (no compression), the PCA model is

invertible. Once the principal components

have been found, the original observa-

tions can be readily expressed as their linear functions as

∑

−

xyx

, and also

the principal components are simply obtained as linear functions of the observations:

.xwy

Both PCA and ICA approaches try to extract components out of a signal; however,

there are essential differences between them. PCA is a purely second-order statistical

method where only co-variances between the observed variables are used in the esti-

mation, assuming that the observed variables are Gaussian and also uncorrelated,

which also implies the independence in the case of Gaussian data.

Contrast to PCA, ICA is a similar generative latent variable model, where the fac-

tors or independent components are assumed to be statistically independent and non-

Gaussian – a much stronger assumption that removes the rotational redundancy of the

PCA (factor analysis) model.

Given a mixture of components (signals), extraction of the independent components

(independent signals) from the mixture can be accomplished based on either of the

following approaches:

Nonlinear decorrelation

Components and are independent if the components and are uncorre-

lated, and the transformed components and are uncorrelated, where

and are some suitable nonlinear functions.

)(

yg )(

()g ()h

The question is: what are suitable functions? The answer can be explored using the

principles of estimation theory and information theory. Estimation theory proposes

maximum likelihood method whereas information theory recommends the use of

mutual information as the measures for independence. It is proven as expected that

mutual information and maximum likely-hood are innately connected.

Non-Gaussianity

The second approach is based on the following that according to the central limit

theorem, sums of non-Gaussian random variables are closer to Gaussian than the

original ones. Therefore, if we have a linear combination

∑

xby

of the ob-

served mixture variables (which, due to the linear mixing model, is a linear combi-

nation of the independent components as well), this will be maximally non-Gaussian

if it equals to one of the independent components. This is because if it were a real

mixture of two or more components, it would be closer to a Gaussian distribution,

due to the central limit theorem [8].

Thus, the problem of extracting independent components is equivalent to finding

the local maxima of non-gaussianity of a linear combination

∑

xby

under the

constraint that the variance of is constant. Each local maximum gives one inde-

pendent component.

To measure non-Gaussian practically, we could use, for example, the kurtosis, a

higher-order cumulant, which is a form of generalizations of variance using higher-

order polynomials. Cumulants have interesting algebraic and statistical properties,

leading to their essential roles in the theory of ICA.

Bell et al [9] proposed using entropy as the measurement of information.

*log( )

p= p

∑

(1)

And the gradient training rule has been proven to be

(1 2 )

−

⎡⎤

Δ∝ +−

⎣⎦

(2)

The inspiration behind the ICA-based image fusion can be illustrated in figure 6. In

the figure PCA approaches shows vertical projection. While the projection shows the

principle component of the randomness, the clustered structure of the data will com-

pletely be lost. In fact, clustering structure is not visible in the co-variance or correla-

tion matrix on which PCA is based. ICA promises to overcome these problems.

Fig. 6. What is interesting linear fusion?

Bell et al [10] reported an approach in which images can be expressed as a

combination of independent components. Mathematically we have:

CWI

∗

(3)

where I is the transformed signals of the image, C is the independent (information)

components of the image and W is the trained weights, respectively.

If we apply ICA onto the mixture of two fusing images, we will have

(

)

12 1 2

(| ) * |

IWCC=

(4)

Consider a linear fusion of images, we have

(

)

12 1

(* * ) * * *aI bI W aC bC+= +

(5)

The simple transformation shows that linear fusion of images actually equal to the

fusion of information (Independent Components) from both images. From the per-

spective of information, the fusion is mainly aimed at retaining maximum information

from original images.

Linear image fusion is not only the fusion of information; it also offers the superb

efficiency computation and ensures the output of fusion will be a visually acceptable.

However, as evidenced in fusion-by-averaging, a linear fusion scheme using fixed

weights would be ineffective in producing good results for diverse fusing images.

Therefore an algorithm, which can dynamically adapt to the fusing images and adjust

the weights so that maximum information can be retained from fusing images, is in

need, motivating the design of the ICA-based image fusion. The framework of the

ICA-based image fusion is briefed as follows and illustrated in figure 7.

1. Transform original images to signals (each image become one signal 1xN)

2. Combine all signals (images) into one mixture of signals (nxN: n: number of im-

ages)

3. Running ICA on the mixture of signals to gain the highest entropy (most informa-

tion) signals output

4. Retransform the calculated signals to become algorithm’s output fused image.

Fig. 7. ICA in image fusion concept.

The proposed ICA approach in image fusion has the following advantages. The

fused image retains the maximum information from the fusing images. As discussed

in section 3, the ICA algorithm ensures that each extracted output is the local maxi-

mum of entropy or maximum of information. The characteristic is obtained based on

adaptive neural network training using the fusing images as training inputs which

leads to the second advantage of the proposed method.

The linear combination weighting of fusing images is determined adaptively de-

pending on specific given fusing images. This gives the approach great effectiveness

in solving the fusion problem dynamically and ensures that a maximum information

fused image will be produced regardless of fusing images.

The method also provides an efficient solution to the image fusion problem. As we

can see, the ICA training is the most expensive part of the fusion scheme. The ICA

training performance is largely dependent on the number of images to be fused. For-

tunately, the number of fusing images is normally limited at 2-3 images. At un-

optimized code and learning step size, the algorithm usually takes less than a minute

to produce the fusion result. It can also be expected that for the video fusion, the ICA

training may be performed only for each of Group of Pitcures to determine the fusion

weights, aimed at achieving a realtime video fusion performance.

4 Experimental Results

We have used a simple ICA algorithm for the image fusion of various types of im-

ages, including facial images (with and without glasses), remote sensing & surveil-

lance images, multi focus images. The visual comparisons of pre-fused and post-

fused images are given in figure 8.

The right most images are the fusion results of the two

corresponding left side images

Fig. 8. Fusion images using ICA.

The fused images by the proposed ICA approach are compared to those produced by

other approaches. The criterion for comparison is the entropy, calculated by equation

(1), of fused images. The fused images as well as Matlab implementation is available

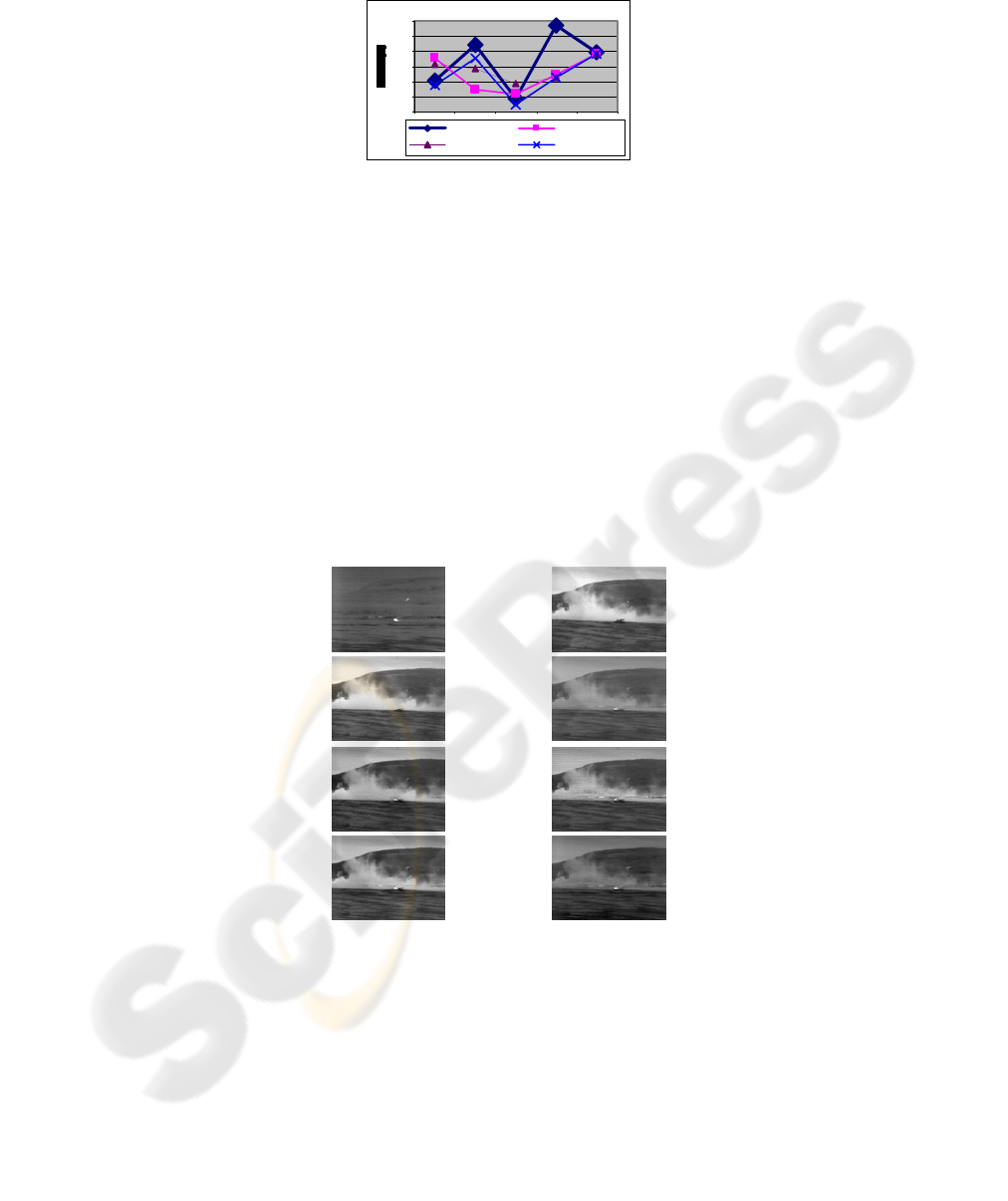
on our website. As showed in figures 9 and 10, ICA outperforms performance other

linear fusion approaches such as averaging or PCA. While for other feature-based

approaches, ICA performance is competitively comparable. The visual comparisons

between the ICA-based fusion scheme and several other fusion techniques, namely,

PCA-based, averaging, Laplacian, contrast-based and wavelet-based fusions, are

shown I figure 11.

2,50E+00

3,00E+00

3,50E+00

4,00E+00

4,50E+00

5,00E+00

5,50E+00

Air View 03 Fac es Learning Faces 2 660-2-1-2 Pepsi Table

Entropy

Image 1 Image 2 ICA result

Averaging PCA result

Fig. 9. ICA vs. averaging & PCA.

4,60E+00

4,70E+00

4,80E+00

4,90E+00

5,00E +00

5,10E+00

5,20E+00

Air Vie w 03 F a c e s Learning Faces 2660-2-1-2Pepsi Table

ICA r esult Wavelet r esult

Laplaci an r esul t Constrast r esul t

Fig. 10. ICA vs. feature based approaches.

5 Conclusions

We proposed a novel image fusion scheme based on optimizing the weighting of the

fusing images using ICA. It is showed that images are combination of the

independent components and that the r fusion retains information from all the fusing

images. A novel algorithm is presented which, based on specific fusing images,

determines adaptively a specific weight for the linear fusion of images. The algorithm

is based on ICA maximum information principles and provides a fast and efficient

process to the problem of image fusion. The adaptive training offers the effectiveness

in achieving excellent fused image and shows the robustness of the scheme under

various fusion situations.

1: Original IR Image 2: Original TV image

3: PCA fused image 4: Averaging fused image

Fig. 11. Visual comparision of results.

References

1. C. Phol, and J.L. Van Genderen, Multisensor Image Fusion in Remote Sensing: Concepts,

Methods and Applications, International Journal of Remote Sensing, 19(5), pp. 823-854,

1998.

2. T. Twellmann, A. Saalbach, O. Gerstung, M. O Leach and T.W. Nattkemper, Image fusion

for dynamic contrast enhanced magnetic resonance imaging, BioMedical Engineering

OnLine 2004,

http://bmc.ub.uni-potsdam.de/1475-925X-3-35/

3. G. Piella, A general framework for multiresolution image fusion: from pixels to regions,

2002, PNA-R0211,

http://www.cwi.nl/ftp/CWIreports/PNA/PNA-R0211.pdf [2]

4. A. Toet, Hierarchical image fusion, Machine Vision and Applications, 3(1), p.p. 1-11, 1990

5. P.J. Burt and E.H. Adelson, The Laplacian pyramid as a compact image code, IEEE Trans-

actions on Communications, 31(4), pp. 532–540, 1983.

6. H. Li, B.S. Manjunath, and S.K. Mitra, Multisensor image fusion using the wavelet trans-

form, Graphical Models and Image Processing, 57(3), pp. 235-245, May 1995

7. T.A. Wilson, S.K. Rogers and L.R. Myers, Perceptual based hyperspectral image fusion

using multiresolution analysis, Optical Engineering, 34(11), pp. 3154-3164, Nov 1995

8. A. Hyv¨arinen, J. Karhunen, and E. Oja, Independent Component Analysis. John Wiley &

Sons Ltd, 2001.

9. A. J. Bell and T. J. Sejnowski, “An information-maximization approach to blind separation

and blind deconvolution,” Neural Computation, 7(6), pp. 1129–1159, 1995.

10. A. J. Bell, T. J. Sejnowski, and M. S. Bartlett, The independent components of natural

scenes are edge filters, Society for Neuroscience Abstracts, 23(1), p. 456, 1997