Modular Statistical Optimization and VQ Method for

Image Recognition

Amar Djouak, Khalifa Djemal, Hichem Maaref

IBISC Laboratory

40 Rue du Pelvoux, 91025 EVRY Cedex.

Abstract. In this work, a modular statistical optimization method enriched by

the introduction of VQ method dedicated to obtain the effectiveness and the op-

timal comuting time in image recognition system is poposed. In this aim, a

comparative study of two RBF and an SVM classifiers are carried out. For that,

features extraction is made based on used image database. These features are

gathered into blocks. The statistical validation results allow thus via the sug-

gested optimization loop to test the precision level of each block and to stop

when this precision level is optimal. In the majority of the cases, this iterative

step allows the computing time reduction of the recognition system. Finally, the

introduction of vector quantization method allows more global accuracy to our

architecture.

1 Introduction

Image recognition is an extensively researched field that has seen many successes but

still many more challenges. One such challenge concerns the great images sets man-

agement wich becomes increasingly complex and expensive in term of computing

time. Also, the semantic richness of these images requires a powerful representation.

These reasons make that the obtaining of the compromise between effectiveness and

optimal computing time is considered as a real challenge. For this purpose, automatic

image recognition in computer vision is a crucial problem, especially if one deals

with heterogeneous images. Considerable efforts have been paid to this problem and

rather promising results, both theoretical and experimental, have been obtained [1, 2,

3] . However, even the most efficient techniques are unable to recognize an image

without errors [4]. Indeed, the similarity search between a request image and the

database images require to understand, find and compare information without inevi-

tably having directly recourse to their contents. Indeed, the image features can be

seen as being structured data, which describe this information, and which can be

applied to all comparison types. This quantification concept is generally interpreted as

classification of features vectors extracted from treated images. We deduce two great

steps, which constitute the traditional way of image recognition process, the features

extraction step that allows to have an image representativeness and the features vec-

Djouak A., Djemal K. and Maaref H. (2006).

Modular Statistical Optimization and VQ Method for Image Recognition.

In Proceedings of the 2nd International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 13-24

DOI: 10.5220/0001224600130024

 SciTePress

tors classification step which allows to obtain a similarity measure between the re-

quest image and the database images. Several features extraction techniques are de-

veloped and used in images recognition systems. The extracted features vary from the

low to the high level image description (color, shape, geometry, semantic knowl-

edge... etc) [5, 6, 7]. These techniques often differ by their results quality obtained in

various applications. Their generalization is thus very difficult to implement since

they were initially developed for specific applications. Since one is interested in this

work in the heterogeneous images recognition, the use of only one features category

can carry out to erroneous results. As for the features extraction, several classification

techniques are used. The majority of these methods [8, 9, 10, 11] have a weakness to

manage high dimension data. That generates consequent computing times and less

precise results. The classification methods based on learning concept [12, 13, 14]

permit to obtain better computing times and more precise results. A specific fea-

tures combination is used in [15]. This choice is justified by the fact that this combi-

nation allows to obtain the best possible images representativeness, which is robust to

the geometrical variations and noises deterioration. In fact, the chosen features in-

clude low-level, wavelet transform and Trace transform features. For classification

step, the radial basis functions (RBF) networks and support vector machines (SVM)

were selected. This choice is justified by the faculty of these two classifiers to obtain

good classes separability and by their effectiveness in term of computing time.

Moreover, these techniques permit to have fluidity and processing simplicity, which

make that they are appropriate to real time applications like image recognition and

search field. Generally, the great challenge of any classification technique is to solve

the high dimensionality problems. Indeed, the data coming from concrete training

problems often appear in high or very high dimension: i.e. that a great number of

variables was measured for each training example. Moreover, the we proposed an

image search method based on great number features extraction. The extracted fea-

tures gave good images representativeness, but the generated high dimensionality on

the classification step deteriorated the global images recognition system. For this

reason, a resolution of high dimensionality problem tool is essential to be able to

obtain a system that ensures a compromise between precision and computing time. In

this paper, we propose a novel architecture based on an optimal features use that is

able to obtain an acceptable precision rate during an optimal search time. In section 2,

the modular statistical optimisation is detailed. Its architecture is presented and com-

pared to classical one. In section 3, the used vectorial quantization is exposed and

discussed. The experimental results obtained with an heterogeneous image DataBase

are presented and discussed in section 4. Indeed, this section presents a comparative

study of obtained results with modular statistical optimisation, vector quantization,

and the combination of both.

2 Modular Statistical Optimization

The idea to introduce a system optimization tool was essential when one realized

during the carried out tests that the use of all extracted features could be heavy to

manage. Indeed, more features vectors dimensions are significant more the classifier

has difficulties for their classification. The traditional way that one followed in [15]

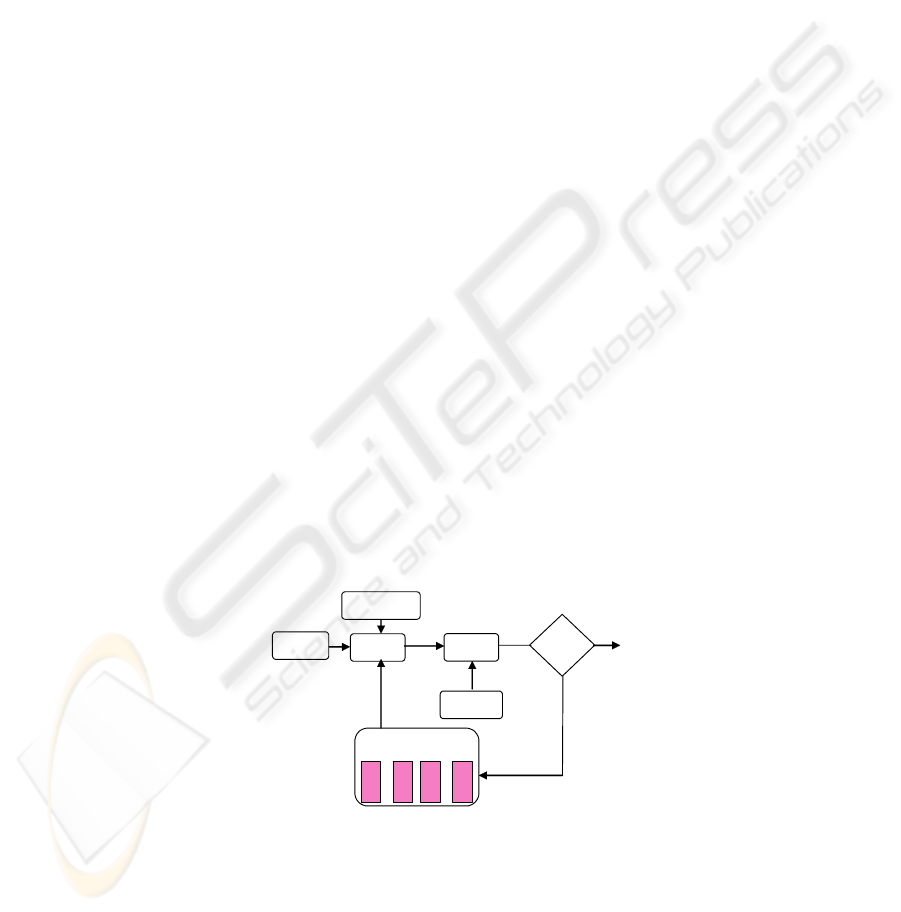
and that one finds in many CBIR systems is a diagram which consists of the use of all

extracted features in the classification step. Unfortunately, this method presents a

great disadvantage, by using all features the classifier manages a great dimensions

number. That involves a consequent computing time what creates a real handicap for

great images databases. In fact, this problem which is the direct result of the high

dimensionality problem was the subject of several works which led to cure it. In [16]

the authors proposed a technique which allows when that is possible to reduce the

SVM training time by using the vectorial quantization technique. The principal idea

was to use the vectorial quantization to replace the training basis by a reduced one. In

the same philosophy, and in order to solve this problem, the proposed architecture of

figure 1 is based on a feedback loop procedure. The principal idea of this architecture

is that instead of using all features in the classification step, one categorizes them on

several blocks or modules and after one tries to obtain the optimal precision with the

minimum of blocks.

2.1 Modular Features DataBase

The introduced modular features database in our proposed architecture (Figure 1)

includes classical features (the two co-ordinates of the image segments medium, the

image segments length, the segment angle compared to the horizontal axis, the gradi-

ent norm average calculated along each segment, the gray levels average of the areas

on the right and on the left of the segments, areas internal contrasts on the left and on

right of the segments, directed differences between the gray levels in the left and right

areas of the segments, the close segments list of each segment), color histograms

features, wavelet transform features (texture features and rotation invariance by

wavelet transform) and finally rotation translation and scaling invariance by Trace

transform. Using all these features one formed four features modules which one can

describe as follows: The first module (b1) gathers the classical features, the second

module (b2) gathers the color features, the third module (b3) the wavelet transform

features and finally the fourth module (b4) the Trace transform features. The follow-

ing table (figure 2) summarizes the obtained features blocks (B1 to B6) by combining

the exposed features modules (b1 to b4). These blocks were used during the experi-

mental tests.

Fig. 1. Modular statistical architecture.

In figure 3, one can see a sample image with its 4 extracted features blocks.

YES

Modular features DataBase

B1 B4 B2

0 ≤ τK ≤ K-δ

Classifier

Request image

Kappa measure

Images DataBase

Error rate

b1 b1b2

1b2

b3b4

Features Blocs B1 B2 B3 B4 B5 B6

Concerned

Modules

b1 b1b2 b3 b1b2b3 b4 b1b2b3b4

Fig. 2. Used features blocks table.

2.2 Classification

The classification block is the tool that makes it possible to obtain a similarity meas-

ure between the database images features vectors and the image request one. In our

application, one used three algorithms, two for RBF and the third for SVM.

2.2.1 RBF Classifiers

Among existing neural networks, one can quote RBF classifier (radial basis function)

which is one of the most used feedforward networks. That is due to the fact that it

uses the local classification principle based on local kernel functions. These functions

give useful answers for restricted field values, their influence field. The kernel func-

tions concept is very significant because they solve the classes separability problem

for the no linearly separable cases. Also, RBF networks can also be built extremely

quickly. This last point is very important for our application, which requires a fast

and simple classifier. In this work one has used two RBF algorithms. The first one is

the RCE algorithm (restricted coulomb energy) introduced by Reilly, Cooper and

Elbaum [17]. This algorithm is inspired by the system particles loads theory. The

algorithm principle is based on the modification of the network architecture in an

iterative way during the training. The intermediate neurons are added only when that

is necessary. The second algorithm is the DDA algorithm (Dynamic Decay Adjust-

ment) [18] which uses at the same time the evolutionary structure of the RCE algo-

rithm and the management possibility of each prototype radius individually. This

radius is related to its closer neighbors. Moreover, a conflict problem exists at the

training phase with the RCE algorithm. This problem is solved with DDA algorithm

with the use of two thresholds instead of one for the RCE algorithm.

2.2.2 SVM classifiers

The SVM algorithms were developed in the Nineties by Vapnik [14]. They were

initially developed for supervised binary classification. They are particularly effective

because they can solve great features numbers management problems. They ensure a

single solution (not local minimum problems as for neural networks) and they pro-

vided good results on real problems. Geometrically, the SVM are the closest vectors

to the optimal hyperplane that separates the two classes internal representations space.

The algorithm in its initial form amounts seeking a linear decision border between

two classes. But this model can be considerably enhanced while being projected in

another space, which makes it possible to increase the data separability. One can then

apply the same algorithm in this new space in order to obtaining a non-linear decision

border in initial space. In this work, one uses LS SVM algorithm (least squares SVM)

−

[19]. This algorithm is based on a different optimization criterion formulation. In-

deed, it based on a least square transformation which transforms the problem into a

Fig. 3. Obtained features blocks for a sample image.

simple linear problem. Also, LS SVM algorithm proposes a linear resolution of the

problem equations to be optimized without using the complex standard SVM quad-

ratic programming. This choice is justified also by its implementation simplicity; its

good separation effectiveness and its optimal computing time.

2.3 Statistical Optimization

Our architecture is mainly based on Kappa measure [20], which is computed from

obtained confusion matrix after classification step. Indeed, this measure is the tool

that allows validating obtained classification results with each introduced features

block. Also, this measure determines the total agreement between classification re-

sults. Theoretically, the equation (1) makes it possible to determine Kappa value K,

where P

is the observed probability and P

is the expected probability [20].

In our case, this agreement depends on the found images precision rates for all re-

quest images constituting the test database. A one confusion matrix is obtained and

then only one Kappa value for each introduced features block. One can thus summa-

rize the modular statistical procedure as follows: For a given request image one intro-

duces to classifier the first features block B1. One calculates the Kappa value of the

(1)

segments length

average

co-ordinates of

segment average

segment angle

average

gradient norm

average

etc....

Wavelet

transform features

b1 b2 b3 b4

1,47

2,65

5,65

3,52

1,41

2,51

5.41

21.41

32.77

11,4

15,41

5,74

1.95

33,47

24,14

11,41

11.63

2,41

1.25

15,74

R114

G154

B87

Triple

Trace feature

1,487

corresponding confusion matrix. If this value is included in a given interval, one

estimates that the result is good, the search for similar images is finished. But if the

obtained Kappa value is not included in this interval, then the feedback loop is acti-

vated, which implies the use of another block. These steps are repeated until one

obtains a Kappa value included in the considered interval. The selection criteria

which one used to fix the interval thresholds is based on the following methodology:

After experimental obtaining of the real precision results which based on the good

found images number for each request image, one determines a P

parameter ob-

tained as follows: P

= real obtained precision rate/ 100 (currently, obtaining P

done in experiments, but it could become automatic). This parameter is used to cal-

culate the error rate τ = 1- P

It should be noted that for each features block one

obtains only one error rate value. In the same way, for the same features block one

obtains only one Kappa value calculated from the corresponding confusion matrix.

Thus, the product (τ. Kappa) is the parameter which one introduced to create relation

between the experimental obtained results and statistical estimates provided by Kappa

measure. The following condition is to be satisfied to validate or not the expressed

precision at the classifier output each features block: 0

≤

τ.K

≤

K- δ

. Where τ is the

error rate value calculated in experiments for each introduced features block. K is the

calculated Kappa value from confusion matrix corresponding to each introduced

features block. δ

is a constant number equal to N.K. N is fixed according to the

desired precision (generally N∈[0.9, 1[). Finally, it should be noted that proposed

architecture could not guarantee a computing time reduction. Indeed, for disturbed

images or which have a great semantic complexity, it may be that one has recourse to

several iterations until coming to the use of the last block which gathers all extracted

features. In this case, one will not gain in time computing but one will be certain for

this case, the use of all features was a need. In other words, one not gain in time but

one gain in term of data classification optimality because one does not use more data

that it is necessary for classification.

3 Vector Quantization

Generally, compression by Vector Quantization (VQ) accepts an input vector X of N

dimension and replaces it by a vector y having with more same dimension belonging

to a dictionary which is a finished vectors codes set, also called classes, or barycen-

tres since those are calculated by an iterative average of vectors X. The quantification

step (according to a dictionary built starting from a training set) rests on the KNN

method : a vector X to be classified will be affected with one of the classes under

the condition which this assignment generates the smallest distortion. However, this

assignment implies a binary choice, i.e. vector X must necessarily belong to the class

to which the barycentre is its nearer close (according to Euclidean distance ). This

assignment rule can appear too idealistic whenever the distances between vector X

and two barycentres are very close. In this case, one or the other of these barycentres

could be appropriate, according to one or more criteria which can be based on some

statistical properties or criteria others that the only Euclidean distance. In our work,

the vector quantization will be useful to making it possible to standardize the features

distribution in the images/ features tables. The aim of this standardization is to bal-

ance the influence of each feature type. Indeed, the bias data problem could deterio-

rate of global system accuracy. Moreover, vector quantization is used in this paper to

reduce data dimensionnality generated by the great nember of used features. One can

find the same philosophy is [16]. Lebrun and all were used VQ technique to reduce

generated high dimensionnality by using SVM classifiers.

The principal idea is to train the SVM classifier on a representative basis of the initial

Database, but with a reduced examples number. LBG algorithm [16] (used in diction-

ary construction step) is applied in order to reduce this examples number. The aim is

to reduce the training time and to obtaind a quick rejection of the bad parameters for

the model choice. The training base size increases with each iteration, until the

improvement of the classification rate improvement becomes lower than a chosen

threshold.

4 Experimental Results

In this section, a comparative study of three classifiers (RBF-RCE, RBF-DDA and

LS-SVM) is carried out and that by using the architecture based on modular optimiza-

tion which one proposed. These three classifiers were applied to the images features

blocks in order to recognize images in heterogeneous images database case. For that,

one used the features blocks which one mentioned previously. The objective being to

reduce when that is possible the image retrieval system computing time. Also, an

other comparative study is carried out between modulat stististical optimisation and

vector quantization method wich is used for high dimensionality reduction in [16].

Finally, the results of the combination of both is exposed and show a small improve-

ment of obtained accuracy. The obtained results in this section are based on the ex-

tracted features from the image database with 1000 images. A sample of those images

is given in figure 4. Statistical optimization thus allows a precision comparative

evaluation of each of the three used classifiers. The figure 6 graphs are an obtained

error rates representation with samples of requests images test database. Those rates

are given after a recall processing for each image.

Fig. 4. Sample of used heterogeneous image database.

4.1 Comparative Study Results of the Three Used Classifiers

With the same images features, and with using our proposed architecture for each one

of the three chosen classifiers (RBF RCE, RBF DDA and LS SVM classifiers), one

obtained the precision results shown in figure 5. With RBF-RCE, one notices the

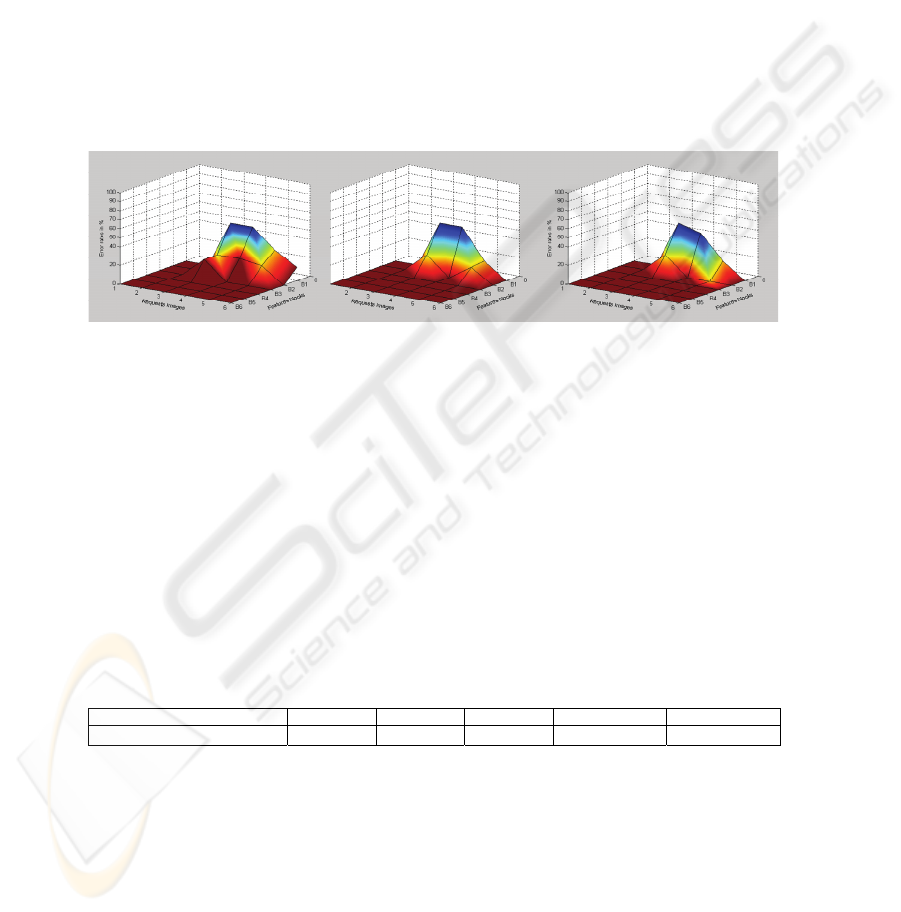
modular architecture utility for requests images 1 and 2 since one obtains a null error

rate with the use of the first block (classical features). The requests images 3, 4, 5

and 6 results show well the features modules iterative addition influence on the pro-

gressive improvement of the corresponding error rates. It is also noticed that for all

used requests images one arrived at an optimal result without using all features mod-

ules (figure 5). With RBF-DDA, one notices the same phenomenon with an obtained

result improvement. Indeed, it is noticed that one arrived more quickly at an optimal

result for requests images 3, 4 and 6 (figure 5). With LS-SVM, one obtains the best

results among the three algorithms. Indeed one notice on figure 5 that there was more

speed to obtain a null error rates in the request image 5 case. Then, one deduces that

modular optimization made it possible to obtain an optimal result with the three used

classifiers without using inevitably all extracted features. However, one notices a

greater convergence to optimal result using SVM classifier. This superiority is ex-

plained by the SVM superiority to manage features vectors great dimensions.

(A) (B) (C)

Fig. 5. Obtained error rates for each classifier. (A): Obtained error rates for RBFRCE classifier,

(B): Obtained error rates for RBFDDA classifier, (C): Obtained error rates for LS SVM classi-

fier.

4.2 Comparative Study Results Between our Method and Vector Quantization

Method

In order to evaluate the effectiveness of our proposed method, an experimental com-

parison is carried out between the obtained results with modular statistical optimisa-

tion and those obtained with a very used method in the dimensionality reduction ap-

plications: the vector quantization method (VQ). To this end, we used the VQ algo-

rithm in order to reduce dimensions of our features vectors. That is done in an itera-

tive way, according to figure 6. This table presents the columns number of the dic-

tionary obtained at each VQ iteration. The dictionary construction depends on the

initial features number in the features basis (32 in this study).

Fig. 6. Dictionary columns number for each iteration.

In figure 5 (c) and figure 7, one notices lower error rates with the first VQ iteration in

comparison with those obtained with our approach.

That is explained by our random choice of initial features blocks in our approach. In

VQ method, initial data choice is more optimal because it is based on specific proc-

essing. As an example, for the request image 3, one obtained an error rate of 50%

VQ iterations Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5

Columns number 2 4 8 16 32

using the first features with modular statistical optimization, while with the first itera-

tion of the VQ one obtained an error rate of 20%. However, one notices a faster con-

vergence in the case of the use of modular statistical optimization after the first choice

of the features block. Indeed, for the request image 3, one obtained the same error

rate (20%) for second iteration QV and for the second choice of features block within

the modular statistical optimization. Then, the vector quantization is more precise in

the first iterations than modular statistical optimization since it is based on a method

of successive divisions which gives convergence towards the optimal result in the

first iteration. On the other hand, modular statistical optimization converges more

quickly after the first chosen block. Moreover, in term of time processing, one can see

in figure 8 that our method is faster than classical method wich is based on use of all

images features in the same time. Also, one can see that our approach is slightly faster

than VQ method because our method don’t require a sorting features algorithm like

used LGB algorithm wich is used in global VQ algorithm.

Fig. 8. Processing time diagrams: With vector quantization, (b): With modular statistical opti-

misation, (c): With classical approach.

However, our approach is limited because the modular statistique optimisation is

applicable only if the request image is also an image of used DataBase. In other

words, our approach is not yet able to reduce the processinf time of the global system

with a request image wich is not present in image DataBase. Nevertheless, it is very

useful in various fields such as police research files, medical imagery, satellite im-

agery...etc. We note that the computing time considered in figure 8 does not take into

account the computing time relative to DataBase images features extration. This step

is an off line operation. Finally, we specify that obtained precision rates shown in

figures 5 and 7 characterize our architecture performances with a sample of 20 im-

ages among the 1000 images of global DataBase. However, other partial results ap-

prove the results presented in this paper and will be presented in a future work.

Fig. 7. Obtained error rates with vectorial quantization using LS SVM classifier.

4.3 Combination Results

The principle of this combination is as follows: we keep the same modular features

base of section 2.1, we apply the vector quantization method to each module which is

solicited by the modular statistical optimization loop. That brings back to a new

reduced confusion matrix and a new Kappa value. The modular statistical optimiza-

tion procedure remains the same one and the loop will stop when the obtained error

rate is minimal. The proposed architecture is thus based on two data space reduction

steps. This double reduction makes it possible to present the most optimal data input

to classification step. In figure 9, we can note the added value of this space data dou-

ble reduction. Indeed, the precision rates are appreciably better with comparing them

with figure 5 (c) and figure 7. Moreover, we need other tests to validate these first

results. Finnally, we note that the final results depend mainly on the images quality

beause the vector quantization method is based on the features vectors representative-

ness. In the contrary case, the desired complexity reduction is not guaranteed and it

is extremely probable that the iterative process uses all the data relating to the fea-

tures blocks without arriving at an optimal result.

Fig. 9. Combination results with SVM classifier.

5 Conclusion

We propose in this work a statistical modular architecture dedicated to the images

recognition systems. In fact, an extraction of used images database is carried out.

These features are gathered into vectors, which are used as classifier inputs. A modu-

lar features database is then built by gathering the features previously extracted into

blocks. Statistical optimization thus makes it possible via an iterative step to intro-

duce these blocks one by one and to stop the process when the precision error rate

reaches the desired minimum. The interest of this method is that one is not obliged to

use all extracted features to obtain optimal result, which enables us to optimize in

much cases the total system computing time. In the contrary case, and if one does not

gain in time reduction, one gains in optimality because one is certain to have not to

use more data than it is necessary to obtain the optimal result. The outcomes in com-

parative study based on the use of two classifiers kinds show the SVM superiority

compared to RBF networks. That is explained by their great capacity to manage great

information quantities and their separability fluidity. Moreover, a comparative study

is carried out between our proposed approach and vector quantization method, and

obtained results show the effectiveness of our method as well in the precision crite-

rion as in the computing time one. However, our approach is not yet able to reduce

the processinf time of the global system with a request image wich is not present in

image DataBase. Nevertheless, it is very useful in various fields such as police re-

search files, medical imagery, satellite imagery...etc. finally, a double dimension data

reduction strategy is proposed basing on the simultaneous use of modular statistical

iptimisation and vector quantization method. Preliminary results show an improve-

ment of obtained results. Moroevere, more tests are necessary to confirm this obser-

vation. Finally, we project in the future to automate error rate obtaining thus opera-

tion that is necessary to fix the statistical optimization interval and permit to our ap-

proach to be applyed to the requests images which are not presents in initial Data-

Base.

References

1. S. Paek, C.L. Sable, V. Hatzivassiloglou, A. Jaimes, B.H. Schiffman, S.-F. Chang, K.R.

Mckeown, “Integration of visual and text based approaches for the content labeling and

classification of photographs”, ACM SIGIR ’99 Workshop Multimedia Indexing Retrieval,

Berkeley, CA, 1999.

2. S. Sclaroff et A. Pentland, “Modal Matching for Correspondence and Recognition” ,

IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. 17, No. 6, pp 545-561.1995.

3. T.Maenpaa, M.Pietikainen, J.Viertola. “Separating color and pattern information for color

texture discrimination”. In Proc of 16

International Conference on Pattern recognition,

2002.

4. D. Landgrebe, “Information Extraction Principles and Methods for Multispectral and

Hyperspectral Image Data,” Information Processing for Remote Sensing, chapter one, Ed-

ited by C. H. Ghen, World Scientific Publishing, 1999.

5. P. Wu, B. S. Manjunath, S. D. Newsam, and H. D. Shin, “A texture descriptor for image

retrieval and browsing,” IEEE International Conference on Computer Vision and Pattern

Recognition: Workshop on Content-Based Access of Image and Video Libraries, pp. 3–7,

Fort Collins, June 1999.

6. S. Newsam, B. Sumengen, and B. S. Manjunath, “Category-based image retrieval,” IEEE

International Conference on Image Processing, Special Session on Multimedia Indexing,

Browsing and Retrieval, Vol. 3, pp. 596–599, Thessalonika, October 2001

7. A.Winter et C. Nastar, “Differential feature distribution maps for image segmentation and

region queries in image databases” , CBAIVL Workshop at CVPR’99, Fort Collins, Colo-

rado, June 22nd, 1999

8. C.Faloutsos,R.Barber,M.Flickner,J.Hafner, W.Niblack, D.Petc, W.Equitz, “efficient and

effective querying by image content”.J.Intell.Inform.syst.Vol.3. pp. 231-262. 1994.

9. A. Pentland, R.W. Picard et S. Sclaroff “Photobook : Content-Based Manipulation of

Image Databases”, Storage and Retrieval for Image and Video Databases II, Proc. SPIE,

nb.2185, 1994.

10. C. Vertan and N. Boujemaa, "Embedding Fuzzy Logic in Content Based ImageRetrieval",

19th International Meeting of the North American Fuzzy Information Processing Society

NAFIPS 2000, Atlanta, Jul. 2000

11. Yixin Chen, James Z.Wang, Jia Li “FIRM : fuzzily integrated region matching for con-

tent-based image retrieval” ACM Multimedia. pp. 543-545. 2001

12. Takashi Ikeda et Masafumi Hagiwara “ Content-based image retrieval system using neural

networks” International Journal of Neural Systems, Vol. 10, No. 5 . pp.417-424. 2000

13. M. Egmont-Petersen, D. de Ridder, H. Handels “ Image processing with neural networks-

a review” Pattern Recognition Vol. 35, No. 10 pp. 2279-2301, 2002

14. Vapnik,V.“The support vector method” Proceedings of ICANN'97, Lausanne. Switzer-

land. pp.583-588. 1997

15. A. Djouak, K. Djemal, H. Maaref, “ Image retrieval based on features extraction and RBF

classifiers” SSD. 2005. Sousse. Tunisia.

16. Lebrun Gilles, Charrier Christophe, Lezoray Olivier « SVM training time reduction by

vectorial quantization » CORESA'04, pp. 223-226, 2004

17. D.L. Reily, L.N. Cooper, and C Elbaum. “A neural model for category learning”. Biologi-

cal Cybernetics. Vol.45. pp. 35-41. 1982

18. Michael R. Berthold, Jay Diamond “Boosting the Performance of RBF Networks with

Dynamic Decay Adjustment” Neural Information Processing Systems. Vol.7 . pp. 521-528.

1995

19. Jos De Brabanter, “LS-SVM Regression Modelling and its Applications” PHD thesis. June

2004. Catholic university of leuven . Belgium.

20. Cohen, Jacob, 1960. “A coefficient of agreement for nominal scales”. Educational and

Psychological Measurement, Vol. 20 pp. 37–46. 1960