HIDING INFORMATION IN WAV-FILE

Implementation, Analysis and Evaluation

Alkhraisat Habes

Russian Academy of Science, Saint Petersburg Institute for Informatics and Automation RAS,

St. 14 Line, 39,199178, Saint Petersburg, Russian Federation

Keywords: Steganography, Low and band bass filter, Host signal, imbedded signal, stego signal, interpolation, and

modulation.

Abstract: This paper focuses on the problem of Steganography: how can two communicating entities send secret

messages over a public channel so that a third party cannot detect the presence of the secret messages.

Notice that the goal of steganography is different from classical encryption, which seeks to conceal the

content of secret messages. The goal of steganography is to hide messages inside other harmless messages

in a way that does not allow any enemy to even detect that there is a second secret message present. This

paper investigates the implementation of hiding secret message (WAV and image file) inside WAV file

called a BASE or HOST, explores several methods in detail, and attempts to test them out in code, and in

practice, through several examples.

1 INTRODUCTION

The art and science of hiding information by

embedding messages within others; seemingly

harmless messages are called Steganography.

Steganography works by replacing bits of useless or

unused data in regular computer files (such as

graphics, sound, etc) with bits of different, invisible

information. Hidden information can be plain text,

cipher text, or even images and sound wave.

Steganographic “protocols” have a long and

fascinating history that goes back to antiquity. There

are stories of secret messages written in invisible ink

or hidden in love letters (the first character of each

sentence can be used to spell a secret, for instance).

More recently, steganography was used by

prisoners, spies and soldiers during World War II

because mail was carefully inspected by both the

Allied and Axis governments at the time. Postal

censors crossed out anything that looked like

sensitive information (e.g. long strings of digits),

and they prosecuted individuals whose mail seemed

suspicious. In many cases, censors even randomly

deleted innocent-looking sentences or entire

paragraphs in order to prevent secret messages from

being delivered. More recently there has been a great

deal of interest in digital steganography, that is, in

hiding secret messages in communications between

computers.

The recent interest in digital steganography is

fuelled by the increased amount of communication

which is mediated by computers and by the

numerous potential commercial applications: hidden

information could potentially be used to detect or

limit the unauthorized propagation of the innocent-

looking “carrier” data. Because of this, there have

been numerous proposals for protocols to hide data

in channels containing pictures, video, audio, and

even typeset text. Many of these protocols are

extremely clever and rely heavily on domain-specific

properties of these channels. On the other hand, the

literature on steganography also contains many

clever attacks which detect the use of such protocols.

In addition, there is no clear consensus in the

literature about what it should mean for a

stegosystem to be secure; this ambiguity makes it

unclear whether it is even possible to have a secure

protocol for steganography.

2 TERMS USED

In the field of steganography, some terminologies

have developed. The adjectives cover, embedded and

stego were defined at the Information Hiding

274

Habes A. (2006).

HIDING INFORMATION IN WAV-FILE - Implementation, Analysis and Evaluation.

In Proceedings of WEBIST 2006 - Second International Conference on Web Information Systems and Technologies - Internet Technology / Web

Interface and Applications, pages 274-281

DOI: 10.5220/0001257802740281

 SciTePress

Workshop held in Cambridge, England. The term

“cover” is used to describe the original, innocent

message, data, audio, and video and so on. When

referring to audio signal steganography, the cover

signal is sometimes called the “host” signal.

The information to be hidden in the cover data is

known as the “embedded” data. The “stego” data is

the data containing both the cover signal and the

“embedded” information. Logically, the processing

of putting the hidden or embedded data, into the

cover data, is sometimes known as embedding.

Occasionally, especially when referring to image

steganography, the cover image is known as the

container.

3 TECHNIQUES

There are two approaches for signal representation:

In time domain the signal is represented as a

function of time (vertical axis is amplitude or

voltage and the horizontal axis is time). In the

frequency domain, the vertical axis is still voltage

but the horizontal axis is frequency. Attempts have

been made to hide secret message in WAV signal in

both domains.

The process of encoding a message inside WAV-

file involves 3 essential steps:

1. Preparing the Host signal.

2. Preparing the embedded message.

3. Adding signals together.

3.1 Hiding Data within WAV File in

Frequency Domain

Conventional CD quality audio has a sample rate of

44.1 kHz and an effective frequency range of 0-

22050 Hz. However, the frequency range of human

hearing only extends from 15 Hz up to somewhere

between 15000 and 20000 Hz depending on the

individual. Even those who can hear up to 20000 Hz

cannot hear those very high frequencies well. So

there is the potential to alter the high frequency

range of a sound by inserting a secret message and

have the result be imperceptible. Figure 1: and

Figure 2 illustrate the process of hiding and

extracting embedded message

3.1.1 Preparing the Host Signal

Step 1: Select a good candidate. The host signal

should be long enough to fit the entire embedded

message. It should also be a relatively active signal

that contains a large amount of information in the

low and mid range frequencies in order to mask what

is happening in the high frequencies.

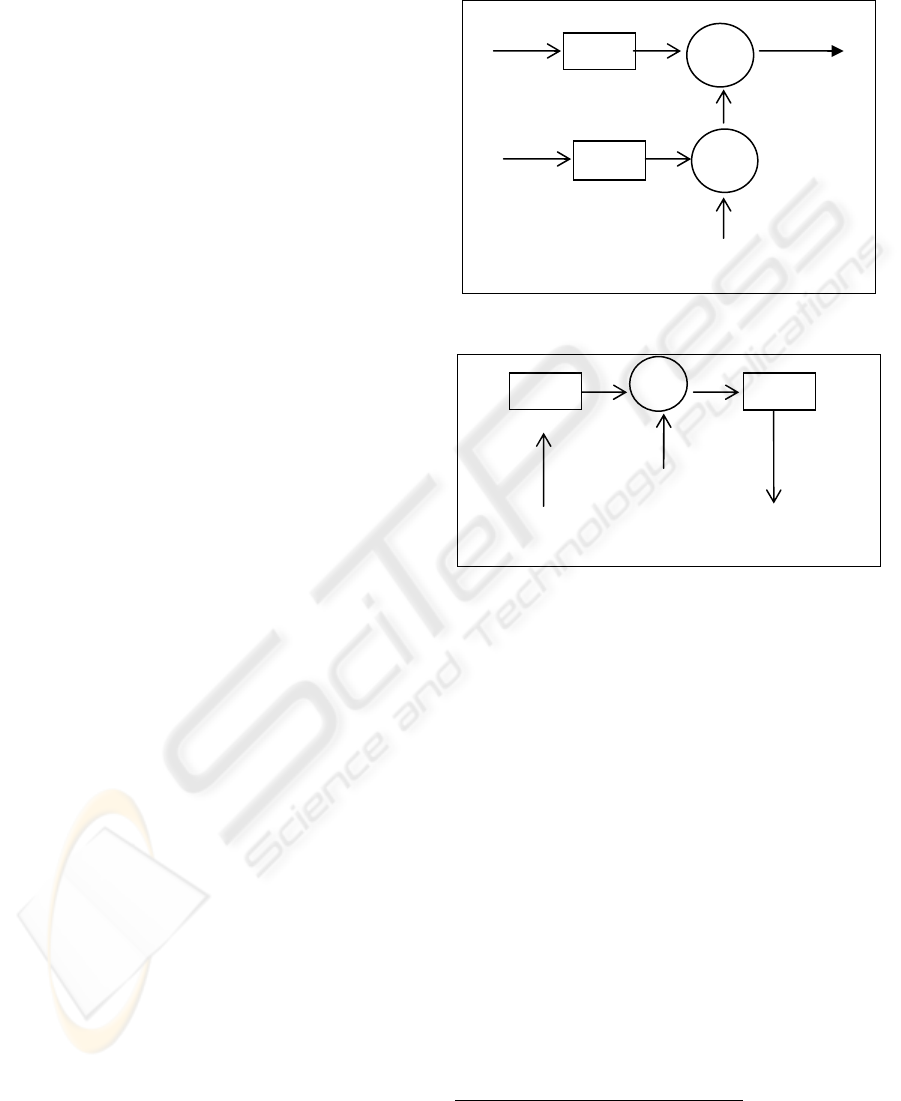
Figure 2: Block diagram of the receiver.

Step 2: Once a good candidate has been selected it

simply has to be sent through a low pass filter with a

cutoff at 17 kHz to cut off the 17-22.050 kHz

frequency range for our embedded message (which

will clear up the upper 5 kHz) Figure 4. Equation (1)

shows low pass filter's equation.

)()()( thtxty

⊗

(1)

Where

)(ty

is the output (magnitude and phase),

)(tx : is the input (magnitude and phase),

)(th : is the impulse response of the filter,

And

⊗

: denotes convolution.

The impulse response of filter is a sequence

of numbers called the filter coefficient. We get the

filter coefficient by simply reading them from the

graph of sinc-function (Figure 3), given by the

following equation:

)(sin)( kTfccTfckh ⋅

⋅

(2)

Where k = -z…, 0 …z

fc: cutoff frequency

K: number of required coefficient

T: sample rate = 1/ sample frequency(fs)

Figure 1: Block diagram of the transmitter.

Host signal

Message

LPF

BPF

∑

Stego

signal

)2cos( Tfspi ⋅⋅⋅

BPF

)2cos( Tfspi ⋅

⋅

Stego signal

LPF

Recovered signal

HIDING INFORMATION IN WAV-FILE - Implementation, Analysis and Evaluation

275

),( xhconvy = : convolves vectors h and x. Let m

= length (h) and n = length(x). Then y is the vector

of length m+n-1 whose k

element is given by:

∑

−+=

jkxjhky )1()()( (3)

The sum is over all values of j which lead to

legal subscripts for h (j) and h (k+1-j), specifically j

= max (1, k+1-n): min (k,m):

y (1) = h (1)*x (1)

y (2) = h (1)*x (2) +h (2)*x (1)

y (3) = h(1)*x(3)+h(2)*x(2)+h(3)*x(1)

y (k) = h(1)*x(n)+h(2)*x(n-1)+ ... +h(n)*x(1)

-30 -20 -10 0 10 20 30

-0.5

0.5

Sinc(x)

-3 -2 -1 0 1 2 3

x 10

0.5

1.5

Freque ncy Hz

phase

l ow p a ss f i lte r

Figure 3: Sinc function

"impulse response of

filter.”

Figure 4: Low pass filter

cut off at 17000.

Figure 5 and Figure 6 illustrate spectrogram of host

signal and filtered host signal.

Time

Frequency

Container Signal

0 5 10 15 20 25 30 35

0.5

1.5

x 10

Time

Frequency

0 10 20 30

0.5

1.5

x 10

pl a ce f o r se cre t m e ssa ge

Figure 5: Host signal. Figure 6: Spectrogram of

filtered Host signal.

3.1.2 Preparing the Embedded Message

The exact method of preparation for the embedded

message depends on its nature (sound, image, etc.),

but they essentially all boil down to formatting the

data so that it fits roughly within a 17-22 kHz

frequency range.

3.1.3 Preparing Embedded Signal

Step 1: Run the embedded signal (Figure 8) through

band pass filter with the band 100Hz – 3.5 kHz

(Error! Reference source not found.), which will

be a small enough band to fit in the upper portion of

the filtered host signal (Figure 9).

-40 -20 0 20 40

0.5

1.5

Frequency

Phase

x 10

Figure 7: Band pass filter with 4kHz window.

Step 2: Modulate the filter signal to fall in the

correct area by multiplying it by a 20 kHz cosine

wave (Figure 10) so that the frequency range of the

embedded message is pushed up 20 kHz.

For i= 1 to length (filter_msg)

)/20002cos(_ ifsmsgFiltMs ⋅⋅⋅

⋅

(4)

End

Time

Frequency

Secret Signal

5 10 15 20

0.5

1.5

x 10

Time

Frequency

5 10 15 20

0.5

1.5

x 10

Figure 8: Embedded signal. Figure 9: Filtered

embedded signal.

Then combine the filtered, modulated embedded

signal with the filtered host signal and we get the

encoded signal with the hidden message in it. The

resulting signal is then scaled to avoid clipping.

Figure 11 shows spectrogram of the stego signal.

))_(max(

signalfinabs

signalfin

signalscaled =

(5)

0 20 40 60 80 100

-1

-0.5

0.5

Amplitude

Time

Frequency

5 10 15 20

0.5

1.5

x 10

Figure 10: 20 kHz cosine.

wave for modulation.

Figure 11: Stego signal.

3.1.4 Preparing Embedded Image

In our experiments we used 256256 × 8-bits gray

scale image (Figure 12)

WEBIST 2006 - INTERNET TECHNOLOGY

276

Figure 12: Example of image that we used in our

experiments.

Step 1: Flat the horizontal lines of pixels together

into one long line of image signal.

Step 2: Interpolate the linear signal to increase

sample rate using Matlab’s interpolation features

(Figure 13 & Figure 14), new sample rate is chosen

so that the resulting signal takes up as much

available space in the host signal as possible, which

is also improve the quality of recovered signal (table

2 page 8).

mult = floor (length (carrier)/length (msg));

msg = interp (msg, mult);

Step 3: Modulate the interpolated signal to fall in

the correct area by multiplying by 20 kHz cosine

wave.

Once both the host and the embedded message have

been prepared, they can be simply added together to

get the stego signal (Figure 15 & Figure 16). The

resulting signal is then scaled to avoid clipping using

Equation (5).

0 5 10 15 20 25 30

-2

-1

Original Signal

0 20 40 60 80 100 120

-2

-1.5

-1

-0.5

0.5

1.5

Interpolated Signal

Figure 13: Original signal. Figure 14: Interpolated

signal.

Time

Frequency

Combined Singnal

0 10 20 30

0.5

1.5

x 10

Time

Frequency

Combine Signa l

5 10 15 2

0.5

1.5

x 10

Figure 15: Stego signal

(host and hidden WAV

signal).

Figure 16: Stego signal

(Host WAV signal &

embedded image).

3.1.5 Recovering Hidden Message

3.1.5.1 Recovering the Hidden Signal

Step 1: Get rid of portions of the host signal that are

in the stego signal. To do this, we band pass filtering

the stego signal to above and below the hidden

message. Set the band to be the modulation

frequency (20 kHz) +/- the max embedded frequency

(3 kHz).

Step 2: Modulate the filtered message back down,

using a cosine signal with the same frequency as

before.

Step 3: Due to additive noise when we did the

addition and higher frequencies due to modulation,

we must low pass filter the demodulated message to

get rid of any extra chatter.

Then we have a signal which very closely resembles

the sent message (Figure 17).

3.1.5.2 Recovering the Hidden Image

Step 1: Modulate the message back down, using a

cosine wave with the same frequency used before, so

the obtained message will be in the correct frequency

range.

Step 2: Scale the message using Equation 5.

Step 3: Resample the image to get original signal

and reshape the data so it can be displayed (Figure

18).

(

)

qpxresampley ,,

: Resample the sequence in

vector x at p/q times the original sampling rate.

(

)

nmAreshapeB ,,

: Return the m-by-n matrix

B whose elements are taken column-wise from A.

Time

Frequency

0 10 20 30

0.5

1.5

x 10

Figure 17: Recovered Signal. Figure 18: Recovered

Image.

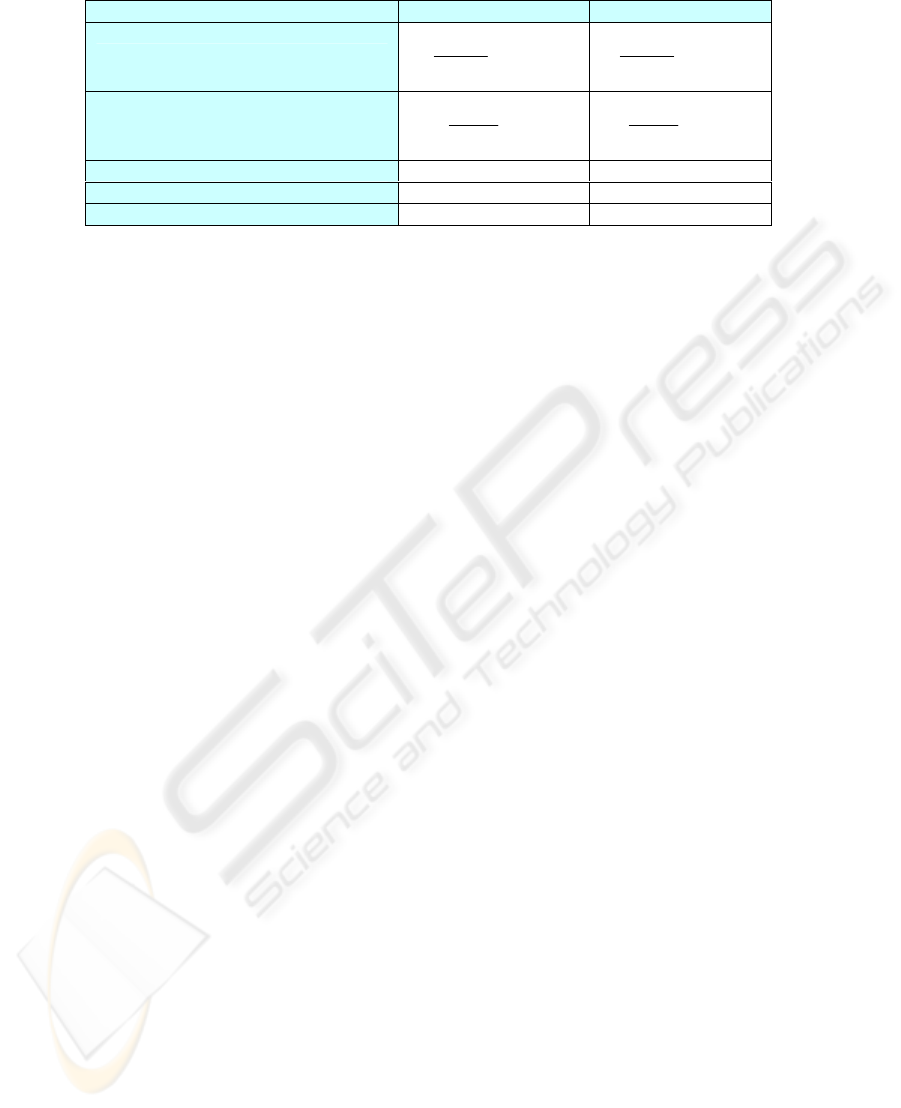
3.2 Hiding Data Inside WAV File in

Time Domain (Figure 19)

Using this approach the signal can be represented as

streams of bits. We can commandeer the least

significant bits to hold of our embedded message by

simply overwriting the data that was already there.

HIDING INFORMATION IN WAV-FILE - Implementation, Analysis and Evaluation

277

For CD quality sound, it is necessary to encode 16

bits per sample at a rate of 44.1 kHz. However,

sound can also be recorded at 8 bits per sample.

Since the majority of the sound signal is stored in

the M most significant bits of the sound code,

changing the lowest N significant bits, where N can

be any power of two up to M/2 bits, leaves the sound

signal somewhat changed in quality and definition,

but still recognizable, and often indistinguishable

from the original.

Figure 19: Block Diagram of Time Domain System.

Starting once again with two signals, a Host

signal and a Messages signal, we choose a value for

N, the number of least significant bits that we wish

to replace in the encoding, and choose an

appropriate length Host. The reason for choosing an

appropriate length Host is to make sure that the full

message can be encoded. Minimum required length

given by:

NPS

TBM

lengthHostMin ×

⎟

⎠

⎞

⎜

⎝

⎛

=__

(6)

Where:

• TBM: The total number of embedded bits in the

message.

• N: The number of bits to be replaced in the

host.

• NPS: The number of bits per sample.

The Base is allowed to be longer. In this

approach we use 2 methods to hide embedded data

inside WAV-file; steps below explain the details of

them. Note we use the same host signal and

embedded signal (Figure 5 & Figure 8) used before,

for testing this approach in both methods.

3.2.1 Method One

3.2.1.1 Preparing the Host Signal

Step 1: Convert the Host signal to stream of binary

bits. Usually the signals are represented as vectors of

decimal values between 1 and -1, in order to convert

them to binary number with 16 bits per sample, it is

necessary to follow the following steps:

• Add 1 to each number to make them all greater

than zero.

• Multiply the obtained vectors by 2^ (15) and

convert each one to a 16-bit binary number.

Step 2: Zero out the 8 least bits in host signal to hold

of our embedded message (Figure 21).

3.2.1.2 Preparing the Embedded Signal

Step 1: Convert the embedded signal to stream of

binary bits

• Adding 1 to each number to make them all

greater than zero.

• Multiply the obtained vectors by 2^ (15) and

convert each one to a 16-bit binary number.

Step 2: Convert the stream of 16 bits binary number

to stream of 8 bits binary number, to achieve this

form, split each 16 bits sample to two 8 bits samples

using:

For i=1 to length (msg)*2

(

)

15],[][ imsgansimsg

()

msg[i],8ightbitshift_R]1[

imsg

End

Step 3: Pad the end of encoded embedded signal

with zeros to make it as same length as Host. This

step is important in encoding because we can’t apply

arithmetic operation on vectors of different length

(Figure 20).

_msg),1)];length(enc-

rrier)th(filt_cazeros(leng [enc_msg; enc_msg

Host signal Embedded message

0 1 2 3 4 5 6 7 8 9 10

x 10

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

1011 0111 1010 1111

1111 1010 0001 0011

1111 0000 10101 1111

1011 0111 0000 0000

1111 1010 0000 0000

1011 0111 1111 0000

1111 1010 1010 0111

Zero out M/2 least

significant bits and place

the embedded message in

lace of the

0 1 2 3 4 5 6 7 8 9 10

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

WEBIST 2006 - INTERNET TECHNOLOGY

278

Time

Frequency

sec ret mess age with zero end

0 5 10 15 20 25 30 35

0.5

1.5

x 10

Time

Frequency

0 10 20 30

0.5

1.5

x 10

Figure 20: Embedded

signal with zero end.

Figure 21: Host signal

after zero out 8 LSBs

3.2.1.3 Adding the Signals Together

Step 1: Combine prepared host signal with the

prepared embedded signal using:

._ msgcontainersignalfinal ⊕=

Step 2: Translate final signal back to vectors

between 1 and -1, in order to be heard by the

human's ears using:

()

.1152__

−

∧×= signalfinalsignalfinal

We get signal with the hidden message in it, which

is closed to host signal (Figure 22).

Time

Frequency

0 10 20 30

0.5

1.5

x 10

Figure 22:

Stego signal.

3.2.1.4 Recovering Hidden Message

Now we have the message signal hidden inside of

the Host signal, we need to come up with a way to

get message signal back. Assuming perfect

transmission, the recovery of our message signal is

quite simple.

Step 1: Convert the stego signal (Figure 23) to

stream of binary bits using the following steps

• Add 1 to each number to make them all greater

than zero.

• Multiply the obtained vectors by 2^ (15) and convert

each one to a 16-bits binary number.

Step 2: Go through every signal and concatenate the

N least significant bits of every received Host signal

into binary message signals of length B.

)15],1[

_(][][

).8],[_(_][

⊕=

jsignal

receivedbinAndimsgimsg

jsignalreceivedleftbinshiftimsg

Step 3: Covert these binary numbers back to decimal

and shift back down to 1 to -1 and we now have a

perfectly recovered message (Figure 24).

Time

Frequency

0 10 20 30

0.5

1.5

x 10

Time

Frequency

0 10 20 30

0.5

1.5

x 10

Figure 23: Stego signal. Figure 24: Recovered

signal.

3.2.2 Method Two

All operations in this method are same as the

operation in method one, just in this method we

increase the total amount of data that can be

embedded in host signal (length of embedded

message) two times longer than in method one,

which also means the required length of Host signal

is decreased half time.

NPS

TBM

lengthHostMin ×

⎟

⎠

⎞

⎜

⎝

⎛

(7)

Using this method we hide just the most

significant bits of embedded message in the least

significant bits of Host signal. Since the majority of

the sound signal is stored in the M most significant

bits of the sound code, we get signal with the hidden

message in it, which is closed to Host signal.

The following example show the required host

length to hide 16 bits message using both methods

discussed above:

Host signal

1100 1111 0101 0011 1111 0101 1111 0111

1111 1111 0000 0101

16 bits embedded signal

Host signal

1100 1111 0101 0011 1111 0101 1111 0111

1111 1111 0000 0101

16 bits embedded signal

0000 0000 11111 11111

16 bits embedded signal

Method 1: By applying Equation (6) minimum

required Host’s length is (16/8)*16 = 32 bits.

Method 2: By applying Equation (7) minimum required host’s

length (16/ (2*8))*16 = 16 bits.

HIDING INFORMATION IN WAV-FILE - Implementation, Analysis and Evaluation

279

Reconstruction the embedded signal is simply

done by adding 1 to received signal, converting

decimal to binary by multiplying by 2^ (15), and

finally shifting the result 8 bits to left. Then we get

signal, which is closed to embedded signal.

Table 1 shows the comparison between method 1

and method 2. Note that:

• TBM: total number of encoded bits in the

message,

• N: number of bits to be replaced in the host,

• NPS: number of bits in sample,

• TBC: total number of bits in the Host signal.

4 RESULTS

To test the Information hiding approaches in time

and frequency domains, we encoded different types

of embedded messages in Host signal in the both

domains. After completing experiments in both

domains, we found that signals of various qualities

can be used simultaneously, one for the host and one

for the message. We also discovered some of the

strengths and weaknesses of doing steganography in

each domain.

A few of the strengths of the frequency domain

are that the host only needs to have the same number

of samples as the message. This means that a longer

message can be hidden in a given base signal than in

the time domain (algorithm 1). Also, frequency

domain approach is easy to implement. Finally, the

frequency domain implementation is also much less

likely than the time domain to be affected by errors

that occur during transmission. On the down side,

this approach has a lot of distortion in the stego

signal. This includes an audible high-pitched cosine

that occurs from the modulation. Also, because of

the filtering that occurs, the message signal has a

limited frequency range and low recovery quality.

When steganography was implemented in the

time domain, we found that it had strengths and

weaknesses opposite of those in the frequency

domain. There was almost no distortion in the stego

signals if only a quarter of the base signal's bits were

used to hide the signal. But there is a little distortion

in embedded signal when we use algorithm 2. Also,

the message could be perfectly recovered and had

no frequency limitations. The disadvantages are that

the host signal needs to be longer than the message,

this is harder to implement. This approach is

extremely easy to corrupt during transmission. This

could be resolved by encoding the message using

hamming code to detect errors. If a hash table was

used to determine which samples had bits replaced,

this could be a very effective method for digital

watermarking. And the problem of host’s length is

solved by using method 2.

We encoded different images -my portraits as

example- inside WAV-signal. The first time there

was a large degree of loss in recovered image. We

decided to expand the image using Matlab’s

interpolation features so that there would be more

redundancy and the image came through very

clearly. This improves the quality of recovered

image, which is intelligible, but darker than the

original table 2 show the effect of interpolation.

5 CONCLUSION

After applying and studying approaches of hiding

information inside WAV-file, as well as touching on

the limitations and possibilities of each approach.

And based on our study, using WAV signal is good

candidate for embedding an acceptable amount of

data. Above algorithms for embedding data can

easily be implemented and do not visually degrade

the host signal to the point of being noticeable.

Table 1: Comparison between method one and method two.

Method 1 Method 2

Host length

NPS

TBM

⎟

⎠

⎞

⎜

⎝

⎛

NPS

TBM

⎟

⎠

⎞

⎜

⎝

⎛

Total number of bits that can be hidden

in the host.

NPS

TBC

⎟

⎠

⎞

⎜

⎝

⎛

NPS

TBC

2×

⎟

⎠

⎞

⎜

⎝

⎛

Distortion of combine signal Acceptable Acceptable

Simple Implementation Weakness strength

Quality of recover signal Better Good

WEBIST 2006 - INTERNET TECHNOLOGY

280

In order to prevent the detection of the

watermark by a user, a hashing algorithm and even

possibly some kind of encoding could be used.

When manufacturers produce CD writers, they could

include the decoder for the encoding method to

determine whether or not it can make copies of the

disk. Once the encoding algorithm is recognized by

the burner it could return a message to the user

stating that the disk is unburnable due to copyright

law.

Since the digital watermark would still be in

place if the users recorded the CD to their hard drive

they still could not burn the music to a CD. In order

for this to work completely, there must also be an

agreement with the makers of "CD-ripping"

software.

REFERENCES

Steven W. Smith, 1997.The Scientist and Engineer’s

Guide to Digital Signal Processing by California

Technical Publishing ISBN 0-9660176-3-3

http://www.dspguide.com/pdfbook.htm.

Wu, Min, Liu, Bede, 2003, Multimedia Data Hiding.

ISBN: 0-387-95426-0. Springer. New York, 1st

edition.

Lenti, Jozsef, 2000. Steganographic Methods. Budapest:

Budapest University of Technology and Economics,

Muhlbauer,

F. Hartung, J.K. Su, B. Girod: “Spread Spectrum

Watermarking: Malicious Attacks and

Counterattacks”, Proc. of SPIE, Security and

Watermarking of Multimedia Contents, vol. 3657,

Jan., 1999.

M. D. Lutovac, D. V. Tosic, B. Filter Design for Signal

Processing using MATLAB and Mathematic L. Evans

Prentice Hall, ISBN 0-201-36130-2.

V. V. Alexandrov, N. D. Gorsky, 1985, Image

Representation and Processing in Recursive Approach,

ISBN: 0-7923-2136-7 Kluwer Academic

F.A.P. Petitcolas, R.J. Anderson, M.G. Kuhn:

``Information Hiding - A Survey'', Proc. of IEEE,

pp.1062-1078, July, 1999.

F. Hartung, M. Kutter: ``Multimedia Watermarking

Techniques'', Proc. of IEEE, pp.1079-1107, July, 1999.

Lenti, Jozsef, 2000. Steganographic Methods. Budapest:

Budapest University of Technology and Economics,

Muhlbauer,

Swanson, 1996, Erik, et al, Steganography in

Signals.http://www.owlnet.rice.edu.

N.F. Johnson. Steganography and digital watermark –

information hiding.

http://www.jjtc.com/Steganography.

F.A.B. Petitcolas. The information hiding homepage -

digital watermarking and Steganography.

WWW:http://www.cl.cam.ac.uk/fapp2/steganography,

1997. University of Cambridge, Computer Laboratory,

Security

Table 2: Effect of interpolation on recovered messages.

Original Image Recovered Image after using interpolation

before hiding process

Recovered Image without using

interpolation before hiding process

HIDING INFORMATION IN WAV-FILE - Implementation, Analysis and Evaluation

281