A PROGRESSIVE REFINEMENT APPROACH

FOR THE VISUALISATION OF IMPLICIT SURFACES

Manuel N. Gamito

∗

Department of Computer Science

The University of Shefﬁeld

Steve C. Maddock

Department of Computer Science

The University of Shefﬁeld

Keywords:

Afﬁne arithmetic, implicit surface, progressive reﬁnement, ray casting.

Abstract:

Visualising implicit surfaces with the ray casting method is a slow procedure. The design cycle of a new

implicit surface is, therefore, fraught with long latency times as a user must wait for the surface to be rendered

before being able to decide what changes should be introduced in the next iteration. In this paper, we present

an attempt at reducing the design cycle of an implicit surface modeler by introducing a progressive reﬁnement

rendering approach to the visualisation of implicit surfaces. This progressive reﬁnement renderer provides a

quick previewing facility. It ﬁrst displays a low quality estimate of what the ﬁnal rendering is going to be

and, as the computation progresses, increases the quality of this estimate at a steady rate. The progressive

reﬁnement algorithm is based on the adaptive subdivision of the viewing frustrum into smaller cells. An

estimate for the variation of the implicit function inside each cell is obtained with an afﬁne arithmetic range

estimation technique. Overall, we show that our progressive reﬁnement approach not only provides the user

with visual feedback as the rendering advances but is also capable of completing the image faster than a

conventional implicit surface rendering algorithm based on ray casting.

1 INTRODUCTION

Implicit surfaces play an important role in Com-

puter Graphics. Surfaces exhibiting complex topolo-

gies, i.e. with many holes or disconnected pieces,

can be easily modelled in implicit form (Desbrun and

Gascuel, 1995; Whitaker, 1998; Foster and Fedkiw,

2001). An implicit surface is deﬁned as the set of all

points x that verify the condition f(x)=0for some

function f(x) from R

to R. Modelling with implicit

surfaces amounts to the construction of an appropriate

function f (x) that will generate the desired surface.

Rendering algorithms for implicit surfaces can be

broadly divided into meshing algorithms and ray cast-

ing algorithms. Meshing algorithms convert an im-

plicit surface to a polygonal mesh format, which

can be subsequently rendered in real time with mod-

ern graphics processor boards (Lorensen and Cline,

1987; Bloomenthal, 1988; Velho, 1996). Ray cast-

ing algorithms bypass mesh generation entirely and

compute instead the projection of an implicit surface

on the screen by casting rays from each pixel into

∗

Supported by grant SFRH/BD/16249/2004 from

Fundac¸

ao para a Ci

encia e a Tecnologia, Portugal.

three-dimensional space and ﬁnding their intersection

with the surface (Roth, 1982; Hin et al., 1989).

Our ultimate goal is to use implicit surfaces as a

tool to model and visualise realistic procedural plan-

ets over a very wide range of scales. The function

f(x) that generates the surface terrain for such a

planet must have fractal scaling properties and exhibit

a large amount of small scale detail. Examples of this

type of terrain generating function can be found in

the Computer Graphics literature (Ebert et al., 2003).

In our planet modelling scenario, meshing algorithms

are too cumbersome as they generate meshes with a

very high polygon count in order to preserve all the

visible surface detail. Furthermore, as the viewing

distance changes, the amount of surface detail varies

accordingly and the whole polygon mesh needs to be

regenerated. For these reasons, we have preferred a

ray casting approach because of its ability to render

the surface directly without the need for an interme-

diate polygonal representation.

The visualisation of an implicit surface with ray

casting is not without its problems, however. When

the surface is complex, many iterations have to be

performed along each ray in order to locate the inter-

section point with an acceptable accuracy (Mitchell,

N. Gamito M. and C. Maddock S. (2006).

A PROGRESSIVE REFINEMENT APPROACH FOR THE VISUALISATION OF IMPLICIT SURFACES.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 26-33

DOI: 10.5220/0001350400260033

 SciTePress

1990). Imaging an implicit surface with ray casting

can then become a slow procedure. This is further

compounded by the fact that an anti-aliased image re-

quires that many rays be shot for each pixel (Cook,

1989).

We propose to alleviate the long rendering times

associated with the modelling and subsequent ray

casting of complex fractal surfaces by providing a

quick previewer based on a progressive reﬁnement

rendering principle. The idea of progressive reﬁne-

ment for image rendering was ﬁrst formalised in

1986 (Bergman et al., 1986). Progressive reﬁnement

rendering has received much attention in the ﬁelds of

radiosity and global illumination (Cohen et al., 1988;

Guo, 1998; Farrugia and Peroche, 2004). Progres-

sive reﬁnement approaches to volume rendering have

also been developed (Laur and Hanrahan, 1991; Lip-

pert and Gross, 1995). Our previewer uses progres-

sive rendering to visualise an increasingly better ap-

proximation to the ﬁnal implicit surface. It allows the

user to make quick editing decisions without having

to wait for a full ray casting solution to be computed.

Because the rendering is progressive, the previewer

can be terminated as soon as the user is satisﬁed or

not with the look of the surface. The previewer is also

capable of completing the image in a shorter amount

of time than it would take for a ray caster to render

the same image by shooting a single ray through the

centre of each pixel.

2 RENDERING WITH

PROGRESSIVE REFINEMENT

The main stage of our method consists in the binary

subdivision of the space, visible from the camera, into

progressively smaller cells that are known to strad-

dle the boundary of the surface. The subdivision

mechanism stops as soon as the projected size of a

cell on the screen becomes smaller than the size of

a pixel. Information about the behaviour of the im-

plicit function f(x) inside a cell is returned by evalu-

ating the function with afﬁne arithmetic (Comba and

Stolﬁ, 1993). Afﬁne arithmetic is a framework for

evaluating algebraic functions with arguments that are

bounded but otherwise unknown. It is a generalisation

of the older interval arithmetic framework (Moore,

1966). Afﬁne arithmetic, when compared against in-

terval arithmetic, is capable of returning much tighter

estimates for the variation of a function, given input

arguments that vary over the same given range. Afﬁne

arithmetic has been used with success in an increasing

number of Computer Graphics problems, including

the ray casting of implicit surfaces (Heidrich and Sei-

del, 1998; Heidrich et al., 1998; de Figueiredo, 1996;

Junior et al., 1999; de Figueiredo et al., 2003). We use

a recently developed form of afﬁne arithmetic that is

termed reduced afﬁne arithmetic (Gamito and Mad-

dock, 2005). Reduced afﬁne arithmetic, in the context

of ray casting implicit surfaces made from procedural

fractal functions, returns the same results as standard

afﬁne arithmetic while being faster to compute and

requiring smaller data structures.

The procedure for rendering implicit surfaces with

progressive reﬁnement can be broken down into the

following steps:

1. Build an initial cell coincident with the camera’s

viewing frustrum. The near and far clipping planes

are determined so as to bound the implicit surface.

2. Recursively subdivide this cell into smaller cells.

Discard cells that do not intersect with the implicit

surface. Stop subdivision if the size of the cell’s

projection on the image plane falls below the size

of a pixel.

3. Assign the shading value of a cell to all pixels that

are contained inside its projection on the image

plane. The shading value for a cell is taken from

the evaluation of the shading model at the centre

point of the cell.

The Rayshade public domain ray tracer imple-

ments a previewing tool that traces rays at the corners

of rectangular regions in the image and subdivides

these regions based on their estimated contrast (Kolb,

1992). Since the ray casting of implicit surfaces is

one instance of the more general ray tracing problem,

the same previewing mechanism could be used here.

In a ray tracer, the process of ray-surface intersection

is performed independently for each ray, with no in-

formation being shared between neighbouring rays.

When a cell is subdivided, on the other hand, the in-

formation about the implicit surface contained in that

cell is reﬁned and passed down to the child cells.

A previewer for implicit surfaces that uses cell sub-

division will, therefore, converge more quickly than

a generic previewer that uses subdivision in image

space, as implemented in Rayshade.

Another previewing method for implicit surfaces

with some similarities to ours was brieﬂy described as

part of a larger work (de Figueiredo and Stolﬁ, 1996).

A subdivision of space using an octree is proposed to

track the boundary of the surface with increasing ac-

curacy. Surface visibility is determined by a painters

algorithm whereby the octree is traversed in back to

front order, relative to the camera, as the cells are ren-

dered on the screen. Our method is more efﬁcient and

less memory intensive in that only the cells that are

known to be visible from the camera are considered.

No time is wasted tracking and subdividing cells that

lie on hidden portions of the surface. The following

sections will explain how each of the steps in our ren-

dering method work.

A PROGRESSIVE REFINEMENT APPROACH FOR THE VISUALISATION OF IMPLICIT SURFACES

2.1 Reduced Afﬁne Arithmetic

A variable is represented with reduced afﬁne arith-

metic (rAA) as a central value plus a series of noise

symbols. In contrast to the standard afﬁne arithmetic

model, the number of noise symbols is constant, be-

ing given by the fundamental degrees of freedom of

the problem under consideration (Gamito and Mad-

dock, 2005). In the rendering method that is being

described in this paper, the degrees of freedom are the

three parameters necessary to locate any point inside

the viewing frustrum of the camera. These parameters

are the horizontal distance u along the image plane,

the vertical distance v along the same image plane

and the distance t along the ray that passes through

the point at (u, v). A rAA variable ˆa has, therefore,

the following representation:

ˆa = a

+ a

. (1)

The extra noise symbol e

is included to account

for uncertainties in the ˆa variable that are not shared

with any other variable. Non-linear operations on

rAA variables are performed by updating the a

, a

and a

noise coefﬁcients with new uncertainties re-

lated to the u, v and t view frustrum distances and

clumping all other uncertainties into the a

coefﬁ-

cient.

For an implicit surface, the vector f(x) at some

point x in space can be described in rAA format as

a tuple of three cartesian coordinates, with the repre-

sentation in (1), and where the noise symbols e

, e

and e

are shared between the coordinates. Each co-

ordinate has its own independent noise symbol e

with i =1, 2, 3. The rAA representation

x of the

vector x describes not a point but a region of space

spanned by the uncertainties associated with its three

coordinates. Evaluation of the expression ˆy = f(

leads to a range estimate ˆy for the variation of f(

x) in-

side the region spanned by

x. Knowing ˆy, the average

value ¯y and the variance y for that range estimate

can be computed as follows, based on the representa-

tion in (1) for an rAA variable:

¯y  y

, (2a)

y  |y

| + |y

|. (2b)

The range estimate ˆy is then known to lie inside

the interval [¯y −y, ¯y + y ]. If this interval con-

tains zero, the region spanned by

x may or may not

intersect with the implicit function. This is because

afﬁne arithmetic (both in its standard and reduced

forms) always computes conservative range estimates

and it is possible that the exact range resulting from

x) may be smaller than ˆy. What is certain is that

if [¯y −y, ¯y + y ] does not contain zero the re-

gion spanned by

x is either completely inside or com-

pletely outside the implicit surface and therefore does

not intersect it.

2.2 The Anatomy of a Cell

A cell is a portion of the camera’s viewing frustrum

that results from a recursive subdivision along the u,

v and t parameters. Figure 1 depicts the geometry

of a cell. It has the shape of a truncated pyramid of

quadrangular cross-section, similar to the shape of the

viewing frustrum itself. Four vectors, taken from the

camera’s viewing system, are used to deﬁne the spa-

tial extent of a cell. These vectors are:

The vector o This is the location of the camera in the

world coordinate system.

The vectors p

and p

They represent the horizon-

tal and vertical direction along the image plane.

The length of these vectors gives the width and

height, respectively, of a pixel in the image plane.

The vector p

It is the vector from the camera’s

viewpoint and orthogonal to the image plane. The

length of this vector gives the distance from the

viewpoint to the image plane.

The vectors p

, p

and p

deﬁne a left-handed per-

spective viewing system. The position of any point x

inside the cell is given by the following inverse per-

spective transformation:

x = o +(up

+ vp

+ p

= o + utp

+ vtp

+ tp

. (3)

+ v

+ p

)

Figure 1: The geometry of a cell. The vectors show the

three medial axes of the cell.

The spatial extent of a cell is obtained from the

above by having the u, v and t parameters vary over

appropriate intervals [ u

], [ v

] and [ t

We must consider how to compute the rAA represen-

tation

x of this spatial extent. To do so a change of

variables must ﬁrst be performed. The rAA variable

ˆu = u

+ u

will span the same interval [ u

]

as u does if we have:

=(u

+ u

)/2, (4a)

=(u

− u

)/2. (4b)

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

Similar results apply for the v and t parameters.

Substituting ˆu, ˆv and

t in (3) for u, v and t, we get:

x = o + t

+ t

+ u

+ v

+ t

(5)

The ﬁrst line of (5) contains only constant terms.

The second and third lines contain linear terms of the

noise symbols e

, e

and e

. The fourth line contains

two non-linear terms e

and e

, which are a con-

sequence of the non-linearity of the perspective trans-

formation. Since a rAA representation cannot accom-

modate such non-linear terms they are replaced by the

independent noise terms e

, e

and e

for each of

the three cartesian coordinates of

x. The rAA vector

x is ﬁnally given by:

x = o + t

+ v

+ p

)

+ t

+ v

+ p

]

(6)

with

= |t

| + |t

|,i=1, 2, 3. (7)

A consequence of the non-linearity of the perspec-

tive projection and its subsequent approximation with

rAA is that the region spanned by

x is going to be

larger than the spatial extent of the cell. Figure 2

shows the geometry of a cell and the region spanned

by its rAA representation in proﬁle. Because the rAA

representation has been linearised, its spatial extent

is a prism rather than a truncated pyramid. This has

further consequences in that the evaluation of f(

is going to include information from the regions of

the prism outside the cell and will, therefore, lead to

range estimates that are larger than necessary. The

linearisation error is more pronounced for cells that

exist early in the subdivision process. As subdivision

continues and the cells become progressively smaller,

their geometry becomes more like that of a prism and

the discrepancy with the geometry of

x decreases

The subdivision of a cell proceeds by ﬁrst choos-

ing one of the three perspective projection parameters

u, v or t and splitting the cell in half along that para-

meter. This scheme leads to a k-d tree of cells where

the sequence of dimensional splits is only determined

at run time. The choice of which parameter to split

along is based on the average width, height and depth

This can be demonstrated by the fact that the terms t

and t

in (5) decrease more rapidly than any of the linear

terms u

, v

and t

of the same equation as the latter con-

verge to zero.

Figure 2: The outline of a cell (solid line) and the outline of

its rAA representation (dashed line) shown in proﬁle. The

rAA representation is a prism that forms a tight enclosure

of the cell.

of the cell:

¯w

=2t

p

, (8a)

¯w

=2t

p

, (8b)

¯w

=2t

u

+ v

+ p

. (8c)

If, say, ¯w

is the largest of these three measures,

the cell is split along the u parameter. The two child

cells will have their u parameters ranging inside the

intervals [ u

] and [ u

], where [ u

] was

the interval spanned by u in the mother cell. In prac-

tice, the factors of 2 in (8) can be ignored without

changing the outcome of the subdivision. This subdi-

vision strategy ensures that, after a few iterations, all

the cells will have an evenly distributed shape, even

when the initial cell is very long and thin.

2.3 The Process of Cell Subdivision

Cell subdivision is implemented in an iterative man-

ner rather than using a recursive procedure. The cells

are kept sorted in a priority queue based on their level

of subdivision. A cell has priority over another if it

has undergone less subdivision. For cells at the same

subdivision level, the one that is closer to the camera

will have priority. The algorithm starts by placing the

initial cell, which corresponds to the complete view-

ing frustrum, on the priority queue. At the start of

every new iteration, a cell is removed from the head

of the queue. If the extent of the cell’s projection on

the image plane is larger than the extent of a pixel, the

cell is subdivided and its two children are examined.

In the opposite case, the cell is considered a leaf cell

and is discarded after being rendered. The two condi-

tions that indicate whether a cell should be subdivided

are:

− u

> 1, (9a)

− v

> 1. (9b)

The values on the right hand sides of (9) are a con-

sequence of the deﬁnition of p

and p

in Section 2.2,

which cause all pixels to have a unit width and height.

A PROGRESSIVE REFINEMENT APPROACH FOR THE VISUALISATION OF IMPLICIT SURFACES

The sequence of events after a cell has been sub-

divided depends on which of the parameters u, v or

t was used to perform the subdivision. If the subdi-

vision occurred along t, there will be two child cells

with one in front of the other and totally occluding

it. The front cell is ﬁrst checked for the condition

0 ∈ f(

x). If the condition holds, the cell is pushed

into the priority queue and the back cell is ignored.

If the condition does not hold, the back cell is also

checked for the same condition. The difference now

is that, if 0 ∈ f(

x) for the back cell, a new cell must

be searched by marching along the t direction. The

ﬁrst cell scanned, at the same subdivision level of the

front and back cells, for which 0 ∈ f(

x) holds is

the one that is pushed into the priority queue. On the

other hand, if the subdivision occurred along the u or

v directions, there will be two child cells that sit side

by side relative to the camera without occluding each

other. Both cells are processed in the same way. If,

for any of the two cells, 0 ∈ f(

x) holds, that cell is

placed on the priority queue, otherwise a farther cell

must be searched by marching forward in depth.

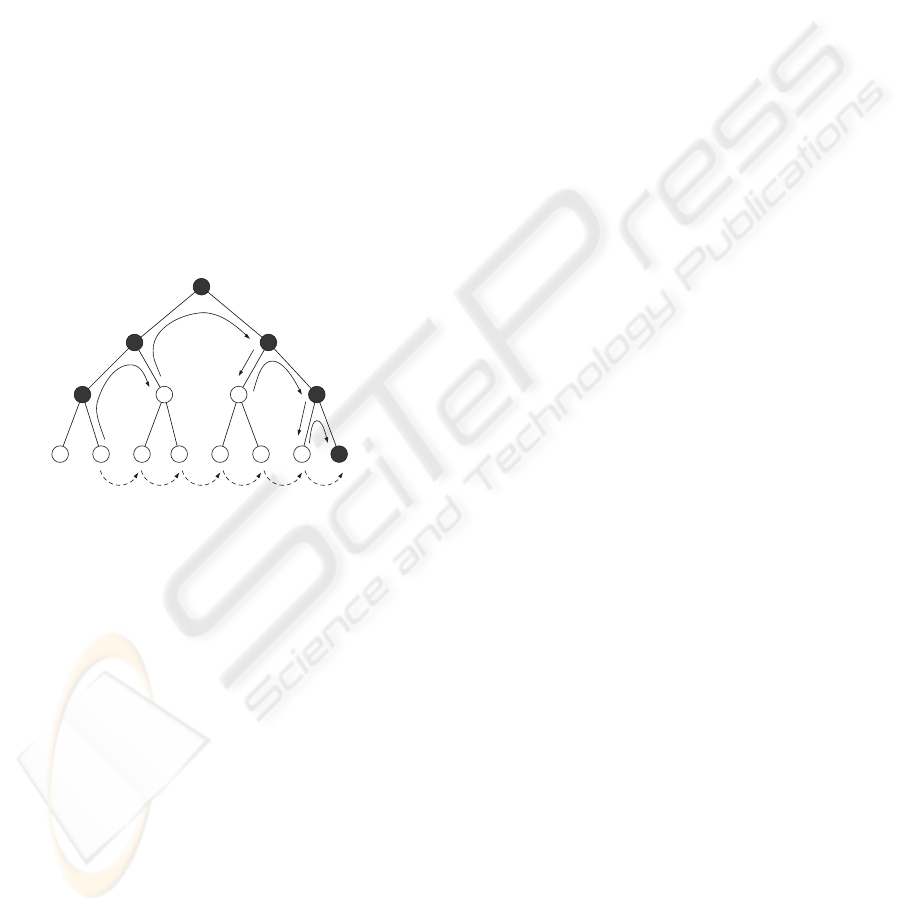
Figure 3: Scanning along the depth subdivision tree. Cells

represented by black nodes may intersect with the surface.

Cells represented by white nodes do not. The solid arrows

show progression by depth-ﬁrst order. The dotted arrows

show progression by breadth-ﬁrst order.

The process of marching forward from a cell along

the depth direction t tries to ﬁnd a new cell that has a

possibility of intersecting the implicit surface by veri-

fying the condition 0 ∈ f(

x). The process is invoked

when the starting cell has been determined not to ver-

ify the same condition. The reason for having this

scanning in depth is because cells that do not intersect

with the surface must be discarded. Only cells that

verify 0 ∈ f(

x) are allowed into the priority queue

for further processing. Figure 3 shows an example of

this marching process. The scanning is performed by

following a depth-ﬁrst ordering relative to the tree that

results from subdividing in t. The scanning sequence

skips over the children of cells for which 0 ∈ f(

x).

The possibility of scanning in breadth-ﬁrst order, by

marching along all the cells at the same level of sub-

division, is not recommended because in deeply sub-

divided trees a very high number of cells would have

to be tested.

As mentioned before, when subdivision is per-

formed along t, the back cell is ignored whenever the

front cell veriﬁes 0 ∈ f(

x). This does not mean, how-

ever, that the volume occupied by this back cell will

be totally discarded from further consideration. The

front cell may happen to be subdivided during subse-

quent iterations of the algorithm and portions of the

volume occupied by the back cell may then be revis-

ited by the depth marching procedure.

2.4 Rendering a Cell

The shading value of a cell is obtained by evaluating

the shading function at the centre of the cell. The cen-

tral point x

for the cell is determined from (6) to be:

= o + t

+ v

+ p

). (10)

During rendering, the shading value of a cell is as-

signed to all the pixels that are contained within its

image plane projection. The centre of a pixel (i, j)

occupies the coordinates c

=(i +1/2,j +1/2)

on the image plane. All the pixels that verify c

∈

] × [v

] for the cell being rendered will

be assigned its shading value. Any previous shad-

ing values stored in these pixels will be overwritten.

This process happens after cell subdivision and before

the newly subdivided cells are placed on the priority

queue. The subdivided cells will overwrite the shad-

ing value of their mother cell on the image buffer. The

same process also takes place for leaf cells before they

are discarded. In this way, the image buffer always

contains the best possible representation of the image

at the start of every new iteration.

2.5 Specifying a Region of Interest

A user can interactively inﬂuence the rendering al-

gorithm by drawing a rectangular region of interest

(ROI) over the image. The algorithm will then reﬁne

the image only inside the speciﬁed region. This is

accomplished by creating a secondary priority queue

that stores the cells that are relevant to the ROI.

When the user ﬁnishes drawing the region, the pri-

mary queue is scanned and all cells whose image pro-

jection intersects with the rectangle corresponding to

that ROI are transferred to the secondary queue. The

algorithm then proceeds as explained in Section 2.3

with the difference that the secondary queue is now

being used. Once this queue becomes empty, the por-

tion of the image inside the ROI is fully rendered

and the algorithm returns to subdividing the cells that

were left in the primary queue. It is also possible to

cancel the ROI at any time by ﬂushing any cells still

in the secondary queue back to the primary queue.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

2.6 Some Implementation Remarks

The best implementation strategy for our rendering

method is to have an application that runs two threads

concurrently: a subdivision thread and a rendering

thread. The rendering thread is responsible for period-

ically updating the graphical output of the application

with the latest results from the subdivision thread. A

timer is used to keep a constant frame refresh rate.

Except for the periodical invocation of the timer han-

dler routine, the rendering thread remains in a sleep

state so that the subdivision thread can use all the CPU

resources.

3 RESULTS

Figure 5 at the end of the paper shows four snap-

shots taken during the progressive reﬁnement render-

ing of an implicit sphere modulated with a Perlin pro-

cedural noise function (Perlin, 2002). The last snap-

shot shows the ﬁnal rendering of the surface. The

large scale features of the surface become settled quite

early and the latter stages of the reﬁnement are mostly

concerned with resolving small scale details.

Figure 4: An implicit surface with two layers (left) and three

layers (right) of a Perlin noise function.

Figure 4 shows an implicit sphere modulated with

two and three layers of the Perlin noise function. Ta-

ble 1 shows the total number of iterations and the

computation time for the surfaces that were rendered

in Figures 4 and 5. The table also shows the computa-

tion time for ray casting the same surfaces by shoot-

ing a single ray through the centre of each pixel. The

results in Table 1 were obtained on a laptop with a

Pentium 4 1.8 GHz processor and 1 Gbyte of mem-

ory. The number of iterations required to complete

the progressive rendering algorithm is largely inde-

pendent of the complexity of each surface. It depends

only on the image resolution and on the percentage of

the image that is covered by the projected surface.

As estimated by the results in Table 1, preview-

ing by progressive reﬁnement is approximately three

times faster than previewing by ray casting without

Table 1: Rendering statistics for an implicit sphere with sev-

eral layers of Perlin noise.

Layers Iterations T ime Raycasting

1 350759 27.8s 1m10.4s

349465 1m16.8s 4m16.7s

359659 3m01.5s 8m51.7s

anti-aliasing. It should be added that these numbers

do not entirely reﬂect the reality of the situation be-

cause, as demonstrated in the example of Figure 5,

progressive reﬁnement previewing already gives an

accurate rendering of the surface at early stages of re-

ﬁnement. From a perceptual point of view, therefore,

the difference between the two previewing techniques

is greater than what is shown in Table 1.

Figure 6 shows two snapshots of a progressive re-

ﬁnement rendering where a region of interest is ac-

tive. The surface being rendered is the same two layer

Perlin noise surface that was shown in Figure 4. The

rectangular ROI is deﬁned on the lower right corner

of the image. The portion of the surface that projects

inside the ROI is given priority during progressive re-

ﬁnement.

4 CONCLUSIONS

The rendering method, here presented, offers the pos-

sibility of visualising implicit surfaces with progres-

sive reﬁnement. The main features of a surface be-

come visible early in the rendering process, which

makes this method ideal as a previewing tool dur-

ing the editing stages of an implicit surface mod-

eler. In comparison, a meshing method would gen-

erate expensive high resolution preview meshes for

the more complex surfaces while a ray caster would

be slower and without the progressive reﬁnement fea-

ture. Our rendering method, however, does not im-

plement anti-aliasing and cannot compete with an

anti-aliased ray caster as a production tool. Produc-

tion quality renderings of some of the surfaces shown

in this paper are typically done overnight, a fact which

further justiﬁes the need for a previewing tool.

It would have been straightforward to incorporate

anti-aliasing into our rendering method by allowing

cells to be subdivided down to sub-pixel size and then

applying a low-pass ﬁlter to reconstruct the pixel sam-

ples. There is, however, one issue that prevents the

use of our method as a production tool and which

makes this implementation effort not worth the while.

As explained in Section 2.1, the computation of range

estimates with afﬁne arithmetic is always conserva-

tive. This conservativeness implies that some cells

a small distance away from the surface may be in-

correctly ﬂagged as intersecting with it. As a conse-

A PROGRESSIVE REFINEMENT APPROACH FOR THE VISUALISATION OF IMPLICIT SURFACES

quence, some portions of the surface may appear di-

lated after rendering. The surface offset error is in the

same order as the size of a pixel. This artifact can be

tolerated during previewing but is not acceptable for

production quality renderings.

We intend in the future to apply our progressive re-

ﬁnement previewing strategy not only to procedural

fractal planets in implicit form but also to implicit sur-

faces that interpolate scattered data points.

REFERENCES

Bergman, L., Fuchs, H., Grant, E., and Spach, S. (1986).

Image rendering by adaptive reﬁnement. In Evans,

D. C. and Athay, R. J., editors, Computer Graphics

(SIGGRAPH ’86 Proceedings), pages 29–37.

Bloomenthal, J. (1988). Polygonisation of implicit surfaces.

Computer Aided Geometric Design, 5:341–355.

Cohen, M. F., Chen, S. E., Wallace, J. R., and Greenberg,

D. P. (1988). A progressive reﬁnement approach to

fast radiosity image generation. In Dill, J., editor,

Computer Graphics (SIGGRAPH ’88 Proceedings),

pages 75–84.

Comba, J. L. D. and Stolﬁ, J. (1993). Afﬁne arithmetic

and its applications to computer graphics. In Proc.

VI Brazilian Symposium on Computer Graphics and

Image Processing (SIBGRAPI ’93), pages 9–18.

Cook, R. L. (1989). Stochastic sampling and distributed

ray tracing. In Glassner, A. S., editor, An Introduction

to Ray Tracing, chapter 5, pages 161–199. Academic

Press.

de Figueiredo, L. H. (1996). Surface intersection using

afﬁne arithmetic. In Davis, W. A. and Bartels, R., ed-

itors, Graphics Interface (GI ’96), pages 168–175.

de Figueiredo, L. H. and Stolﬁ, J. (1996). Adaptive enu-

meration of implicit surfaces with afﬁne arithmetic.

Computer Graphics Forum, 15(5):287–296.

de Figueiredo, L. H., Stolﬁ, J., and Velho, L. (2003). Ap-

proximating parametric curves with strip trees us-

ing afﬁne arithmetic. Computer Graphics Forum,

22(2):171–171.

Desbrun, M. and Gascuel, M. (1995). Animating soft sub-

stances with implicit surfaces. In Cook, R., editor,

Computer Graphics (SIGGRAPH ’95 Proceedings),

pages 287–290.

Ebert, D. S., Musgrave, F. K., Peachey, D., Perlin, K., and

Worley, S. (2003). Texturing & Modeling: A Proce-

dural Approach. Morgan Kaufmann Publishers Inc.,

third edition.

Farrugia, J. P. and Peroche, B. (2004). A progressive ren-

dering algorithm using an adaptive perceptually based

image metric. Computer Graphics Forum, 23(3):605–

614.

Foster, N. and Fedkiw, R. (2001). Practical animation of liq-

uids. In Pocock, L., editor, Computer Graphics (SIG-

GRAPH ’01 Proceedings), pages 23–30.

Gamito, M. N. and Maddock, S. C. (2005). Ray cast-

ing implicit procedural noises with reduced afﬁne

arithmetic. Memorandum CS – 05 – 04, Dept.

of Comp. Science, The University of Shefﬁeld.

http://www.dcs.shef.ac.uk/

∼mag/CS0504.pdf.

Guo, B. (1998). Progressive radiance evaluation using di-

rectional coherence maps. In Cohen, M., editor, Com-

puter Graphics (ACM SIGGRAPH ’98 Proceedings),

pages 255–266.

Heidrich, W. and Seidel, H.-P. (1998). Ray-tracing proce-

dural displacement shaders. In Davis, W., Booth, K.,

and Fournier, A., editors, Graphics Interface (GI ’98),

pages 8–16.

Heidrich, W., Slusallik, P., and Seidel, H. (1998). Sam-

pling procedural shaders using afﬁne arithmetic. ACM

Transactions on Graphics, 17(3):158–176.

Hin, A. J. S., Boender, E., and Post, F. H. (1989). Vi-

sualization of 3D scalar ﬁelds using ray casting. In

Eurographics Workshop on Visualization in Scientiﬁc

Computing.

Junior, A., de Figueiredo, L., and Gattas, M. (1999). In-

terval methods for raycasting implicit surfaces with

afﬁne arithmetic. In Proc. XII Brazilian Symposium

on Computer Graphics and Image Processing (SIB-

GRAPI ’99), pages 1–7.

Kolb, C. E. (1992). Rayshade user’s guide and reference

manual. Draft 0.4.

Laur, D. and Hanrahan, P. (1991). Hierarchical splatting: A

progressive reﬁnement algorithm for volume render-

ing. In Sederberg, T. W., editor, Computer Graphics

(SIGGRAPH ’91 Proceedings), pages 285–288.

Lippert, L. and Gross, M. H. (1995). Fast wavelet based vol-

ume rendering by accumulation of transparent texture

maps. Computer Graphics Forum, 14(3):431–444.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3D surface construction algorithm.

In Stone, M. C., editor, Computer Graphics (SIG-

GRAPH ’87 Proceedings), pages 163–169.

Mitchell, D. P. (1990). Robust ray intersection with interval

arithmetic. In MacKay, S. and Kidd, E. M., editors,

Graphics Interface (GI ’90), pages 68–74.

Moore, R. (1966). Interval Arithmetic. Prentice-Hall, En-

glewood Cliffs (NJ), USA.

Perlin, K. (2002). Improving noise. ACM Transactions on

Graphics, 21(3):681–682.

Roth, S. D. (1982). Ray casting for modeling solids. Com-

puter Graphics and Image Processing, 18(2):109–

144.

Velho, L. (1996). Simple and efﬁcient polygonization of

implicit surfaces. Journal of Graphics Tools, 1(2):5–

24.

Whitaker, R. T. (1998). A level-set approach to 3D recon-

struction from range data. Int. J. Computer Vision,

29:203–231.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

Figure 5: From left to right, top to bottom, snapshots taken during the progressive reﬁnement rendering of a procedural noise

function. The snapshots were taken after 5000, 10000, 28000 and 350759 iterations, respectively. The wall clock times at

each snapshot are 1.02s, 1.98s, 4.18s and 27.80s, respectively.

Figure 6: Progressive reﬁnement rendering with an active region of interest shown as a red frame. Once rendering is complete

inside the region, reﬁnement continues on the rest of the image.

A PROGRESSIVE REFINEMENT APPROACH FOR THE VISUALISATION OF IMPLICIT SURFACES