SPHERE–TREES GENERATION AS NEEDED IN REAL TIME

Marta Franquesa Niub

Departament de Llenguatges i Sistemes Inform

atics

Universitat Polit

ecnica de Catalunya

Omar Rodr

ıguez Gonz

alez

Facultad de Ingenier

ıa

Universidad Aut

onoma de San Luis Potos

Keywords:

Sphere-tree, collision detection, viewing volume, graphics hardware.

Abstract:

In this paper two improvements to speed up collision detection are described. Firstly, a method called oncollide

sphere-tree, OCST for short, is presented. This approach works by detecting collisions among models with

arbitrary geometry using the video cards Graphics Processing Units, GPU. While candidate parts of colliding

objects are being detected, the OCST is constructed for collision evaluation in parallel, at the same time. Thus,

the OCST is created in realtime. Secondly, we have tested two kinds of triangulated representation models for

the same originalobjects. We have evaluated trianglesoup and trianglestrip models to speed up the algorithm

response when computing collisions. The method has been described, implemented and tested for the two

kinds of triangulated models, and the obtained results are shown.

1 INTRODUCTION

Collision detection is a key problem in many areas

of computer graphics (Jimenez et al., 2001; Lin and

Manocha, 2003). Considered as a bottleneck within

real-time environments, several authors have studied

the detection of a collision and multiple solutions

have been proposed and published.

It is well known that to compute collision detec-

tion among several objects, a bounding easy–shaped

wrapper and hierarchies of them are created and used

to cover each involved scene–object. These wrappers

of simple shape allow us to compute intersections in

a quick way, discarding collision faster than using the

geometry of the original object models. The problem

that arises is the efﬁcient managing of the wrapper hi-

erarchies. As the wrappers are usually called bound-

ing volumes (BV), the hierarchies are called BV–

trees. Examples of BV are axis–aligned–bounding–

boxes (AABB), oriented–bounding–boxes (OBB) and

spheres. The most solutions compute the trees in a

preprocessed step and, then, traverse them in a later

animation time. These approaches are cumbersome

and heavy to manage in the whole process. Thus, the

bottleneck of this solution lies in the time step when

the new levels of the tree are created, traversed and

updated. One of the most commonly BV–hierarchy

model used is the sphere–tree.

The hybrid collision detection (Kitamura et al.,

1994), refers to any collision detection method that

ﬁrst performs one or more iterations of approxi-

mate test to study whether objects interfere in the

workspace and then, performs more accurate tests

to identify the object parts causing the interference.

Hubbard (Hubbard, 1995) reports two phases: the

broad phase, where approximate interferences are de-

tected, and the narrow phase where exact collision

detection is performed. O’Sullivan and Dingliana

(O’Sullivan, 1999; O’Sullivan and Dingliana, 1999)

extended the classiﬁcation pointing out that the nar-

row phase consists of several levels of intersection

testing between two objects at increasing level of ac-

curacy (narrow phase: progressive reﬁnement lev-

els) and, in the last level of accuracy, the tests

may be exact (narrow phase: exact level). Fran-

quesa and Brunet (Franquesa-Niub

o and Brunet,

2003; Franquesa-Niub

o and Brunet, 2004) divided the

broad phase in two subphases. In the ﬁrst one, tests

are performed to ﬁnd subsets of objects from the en-

tire workspace where collisions can occur, rejecting

at the same time, all the space regions where interfer-

ence is not possible (broad phase: progressive delimi-

tation levels). In the second subphase, tests determine

the candidate objects that can cause a collision (broad

phase: accurate broad level). Figure 1 summarizes

the complete hybrid collision detection pipeline in-

Franquesa Niubó M. and Rodríguez González O. (2006).

SPHERE–TREES GENERATION AS NEEDED IN REAL TIME.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 11-18

DOI: 10.5220/0001351600110018

 SciTePress

Figure 1: Collision detection pipeline.

cluding all its phases.

On–the–ﬂy generation of the BV–tree is better than

pre–processing because the tree is updated when-

ever needed in real–time and memory is efﬁciently

managed. For some complex scenes, a scene hier-

archy has to be generated in a pre–processing step

and storing additional information about the bound-

ing volume. We have dicussed this goal and we pre-

sented a method named M Ktrees (Franquesa-Niub

and Brunet, 2004; Rodr

ıguez and Franquesa-Niub

005c). BV–trees generation on the ﬂy will not intro-

duce additional overhead during run time because it

is computed by using the GPUs.

In recent times, the availability of high perfor-

mance 3D graphics cards are common in personal

computers. The power and fastness of the built-in

Graphics Processing Units, GPU, and its own ded-

icated memory is being applied to a wider variety

of applications, even those that the creators did not

originally intend to manage. This paper describes

a hardwar–accelerated collision detection scheme.

Bounding sphere–trees are constructed on the ﬂy us-

ing occlusion query extensions of modern GPUs.

In this paper, two improvements are described.

Firstly, a method called on-collide sphere–tree,

OCST, is presented. This approach works by detect-

ing collisions among models with arbitrary geome-

try using the video card’s GPU. While candidate parts

of colliding objects are detected, the OCST is con-

structed for collision evaluation in parallel, at the

same time. Thus, the OCST is constructed in real-

time. Secondly, we have tested two kinds of triangu-

lated models for the same original–objects. We have

evaluated triangle–soup and triangle–strip models to

speed up the algorithm response. A triangle–strip is

a list of triangles where each triangle shares two ver-

tices with the preceding triangle. The ﬁrst three in-

dices of the list, deﬁne a triangle and then each ad-

ditional index deﬁnes another triangle by using the

two preceding indices. More detailed information can

be found in (Rodr

ıguez and Franquesa-Niub

o, 005a;

Rodr

ıguez and Franquesa-Niub

o, 005b).

As already mentioned, the whole structures involved

in the hybrid collision detection phases have usually

been computed as a preprocess to the simulation en-

vironment. Before entering the simulation, the struc-

tures must be loaded in core memory. We present an

algorithm that does not use precomputed BV hierar-

chical structures, but it uses instead an octree–based

sphere–tree created in real-time on needed. The de-

tection of surface overlapping over the sphere–tree

nodes is performed making use of occlusion queries

by exploiting the capacities of modern graphics hard-

ware. The algorithm is aimed at rigid objects moving

in large environments. The narrow phase of the hy-

brid collision detection problem is accelerated. When

many objects interact, main memory is managed more

efﬁciently than the other preprocessed approaches.

The access to secondary storage is improved when

out-of-core techniques are used.

2 RELATED WORK

A bounding volume hierarchy approximates a rep-

resentation of an object as a hierarchical structure,

known as bounding volume tree (BVtree). One of the

most used BVtrees in the literature is the sphere–tree

(Hubbard, 1993). A sphere–tree represents an ob-

ject by sets of spheres in a hierarchical way. Three

methods are commonly used for the construction of a

sphere–tree. The ﬁrst one, consists of ﬁtting spheres

to a polyhedron and shrinking them until they just

ﬁt (Rourke and Badler, 1979). The second one is

based on an octree (Samet, 1990). Thus, the octree–

based sphere–trees (Hubbard, 1996; O’Sullivan and

Dingliana, 1999; Palmer and Grimsdale, 1995; Po-

bil et al., 1992) performs a recursive subdivision in

3D, creating spheres on child nodes that overlap the

surface of the object. And the third and last, the

medial-axis surface method (Bradshaw and OSulli-

van, 2003; Hubbard, 1995; Hubbard, 1996; Quinlan,

1994), uses Voronoi diagrams to calculate the object

skeleton placing maximal sized spheres on it so the

spheres ﬁll the object.

The graphics-hardware-assisted collision detection

algorithms started with Shinya and Forgue (Shinya

and Forgue, 1991), and Rossignac et al. (Rossignac

et al., 1992). After them, a more efﬁcient algorithm

was proposed by Myszkowski et al. (Myszkowski

et al., 1995) using the stencil buffer. Baciu and Wonk

(Baciu and Wonk, 1998) were the ﬁrst to use common

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

available graphics cards to compute image–based col-

lision detection. Vassilev et al. (Vassilev et al., 2001)

use a technique for collision detection in deformable

objects like clothes. Kim et al. (Kim et al., 2003)

use graphics hardware to calculate Minkowski sums

to ﬁnd the minimum translational vector needed to

separate two interfering objects. All those algorithms

involve no precomputation, but perform image-space

computations that require the reading back of the

depth or stencil buffer, which can be expensive on

standard graphics hardware.

Govindaraju et al. (Govindaraju et al., 2003) use

occlusion queries to compute a potentially colliding

set (PCS) in the broad phase, followed by exact colli-

sion in the narrow phase. Fan et al. (Fan et al., 2004)

use occlusion queries to fast detect collision between

a convex object and an arbitrarily shaped object. The

advantage of using GPU based occlusion queries is

that no read back of the depth or stencil buffer is nec-

essary to obtain results. This kind of tests are faster

than image-space computations.

As pointed out in (Kornmann, 1999), in order to

achieve high 3D graphics performance in many ap-

plications, it is essential to use triangle strips be-

cause they can greatly speed up the display of triangle

meshes. Triangle strips have been widely used for ef-

ﬁcient rendering. It is NP-complete to test whether a

given triangulated model can be represented as a sin-

gle triangle strip, so many heuristics have been pro-

posed to partition models into few long strips. In the

literature we can ﬁnd many approaches that treat the

problem to compute triangle–strips. There are several

programs available in the world wide web. One of

a common software is the STRIPE

. This software is

a tool which converts a polygonal model into trian-

gle strips and it is freely available for non commercial

use.

3 OCST REPRESENTATION

MODEL

To cover each candidate object for collision, octree–

based representation for sphere–trees construction is

used. As it is well known, an octree is a hierarchi-

cal structure obtained subdividing recursively in 3D

to form eight child nodes (Samet, 1990; Rodr

ıguez

and Franquesa-Niub

o, 005b). Each one can be repre-

sented with three colors. Black color for child nodes

completely inside the subdividing object. White for

child nodes completely outside. Grey for child nodes

in which the frontier of the object overlaps. Grey

nodes will be subdivided until a user–deﬁned depth

for the octree is reached. When the octree depth

http://www.cs.sunysb.edu/ stripe

Figure 2: Original object and octree–based sphere–tree lev-

els 2, 4 and 6.

is reached, the grey nodes become leaf nodes. An

octree–based sphere–tree is an octree where each

node is bounded by one sphere instead of a cube. Fig-

ure 2 shows an octree–based sphere–tree representa-

tion of a dragon.

A conservative collision detection can be per-

formed by using a sphere–tree based on octrees, with

a certain depth level. The model gives enough prox-

imity to the object’s surface depending on the pre-

speciﬁed user–level.

The cost of creating sphere–trees can be high in

terms of computing resources. Space subdivisions re-

quire ﬂoating–point operations, which are generally

slow on CPU. The octree construction requires hav-

ing the geometry object loaded in core memory aside

the sphere–tree structure. Trying to create a sphere–

tree on simulation run-time cannot be achieved using

only the CPU. Therefore the construction of a sphere–

tree has been treated as a precomputation step to the

simulation. Having and maintaining all the sphere–

tree structures in core memory when many objects are

present, can be expensive during the life cycle of a

simulation.

From the BVtrees construction methods, the sim-

plicity of octree–based sphere–trees makes it good

enough to implement them using graphics hardware

(see section 4). The construction of sphere–trees in

real-time is performed using occlusion queries. Thus,

here, no precomputation is necessary, core memory

is free of hierarchical structures at the beginning of

the simulation because the sphere–trees are created

only on-collision when required. To preserve mem-

ory, only branches of the sphere–tree for the parts

of the objects that potentially can collide are com-

puted. Newly created branches are maintained in

core memory for future use during the simulation

(see section 5). As we will see in next sections, the

use of triangle–strips, instead of triangle–soups, to

model the scene–objects increases the efﬁciency of

the whole collision detection system computing the

wrapper model in real time whenever needed.

SPHERE–TREES GENERATION AS NEEDED IN REAL TIME

Figure 3: Occlusion queries: Some incoming object frag-

ment passes the depth test.

Figure 4: Occlusion queries: No incoming object fragment

passes the depth test.

4 OCST CONSTRUCTION

Different hardware designers have made several oc-

clusion test implementations with differences in per-

formance and functionality. In this way, we can dis-

tinguish three types of occlusion queries. The ﬁrst

one

, returns a boolean answer indicating if incoming

object fragment passes the depth test (see Figure 3,

the occlusion query will return TRUE). The second

one

, returns the number of fragments that pass the

depth test and requires a previous boolean query to

be supported by the graphic card. Thus, two queries

have to be done to know the one answer. The third and

most standard, GL

ARB occlusion query

, is similar

to the last mentioned query, but it returns the samples

of object parts that occlude directly. It does not re-

quire the previous boolean query. Figure 4 shows a

case of no occluded object.

The GL

ARB occlusion query is used in our

method to avoid stalls in the graphics pipeline. This

query can manage multiple queries before asking for

the result of any one, increasing the overall perfor-

mance.

In what follows we describe how the oclusion

query works, and how our method uses of it. Let A

be an arbitrarily shaped object. An OCST root node

for A is constructed creating a box for A: AABB(A).

A bounding sphere for A is created bounding the

AABB(A), with its center as the center of the AABB

http://oss.sgi.com/projects/ogl-

sample/registry/HP/occlusion

test.txt

http://oss.sgi.com/projects/ogl-

sample/registry/NV/occlusion

query.txt

http://oss.sgi.com/projects/ogl-

sample/registry/ARB/occlusion

query.txt

Figure 5: Viewing volume construction: One of the three

viewing volumes and its camera position.

and its radius as half the distance of the AABB ex-

treme vertices: S(AABB(A)). Taking the AABB from

the root node of A, we construct a new level for the

OCST subdividing it in 3D. For each new child node,

a resulting octree subdividing AABB box is assigned

and an overlap test is performed to verify if it can be

a grey node. Occlusion computations are performed

to accelerate the overlap test for the detection of grey

nodes. These computations are based in the fact that,

if the surface of A can be viewed in at least some part

from inside the AABB of an octree node, then A is

overlapping the octree node and the node is marked

grey (see Figure 3). The overlap test performs one,

two or up to three occlusion queries, one for each of

the main axis.

Three requirements are needed for each occlusion

query (See Figure 5): A viewing volume, a camera

position and the occlusion test elements. The viewing

volume is created using an orthographic frustum view

limited by the AABB box of the octree node tested.

The camera position is placed outside the viewing

volume, centered at a box face, looking toward the

box in parallel to a main axis, and with a distance

equal to the length of the box in the looking direc-

tion. The ﬁrst occlusion test element (the occluder),

is the AABB box of the octree node. The second oc-

clusion test element (the possibly occluded objects),

is the surface of A .

An occlusion query reports if one or more occlud-

ers allow the possibility that occluded objects can be

seen from inside a viewing volume. In other words,

if the surface of A can be seen from inside the AABB

box (viewing volume) of the tested octree node, in at

least one of the three main axis, then the surface of A

is overlapping that octree node. If the number of sam-

ples that passed the occlusion query is greater than

zero in at least one of the three queries (for x, y and z

axis), then the surface of A overlaps the tested OCST

node and it it is marked grey. In this case, a sphere

is created bounding the AABB box of the node and is

inserted on the OCST structure.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

Figure 6: Spheres A and B collide iff d ≤ R

+ R

, where

d = |C

− C

5 OCST AND REAL-TIME

COLLISION DETECTION

To achieve collision detection in real-time, OCST

branches are constructed for objects only when it is

needed. Thus, to initialize the animation system it

is only required to load the geometry of the objects

into graphics card’s memory, and construct a root

OCST for each of them at the beginning of the sim-

ulation. The OCST root is initialized with an AABB

and a bounding sphere with the center as the center of

the AABB, and its radius as half the distance of the

AABB extreme vertices.

Let A and B be arbitrarily shaped objects in move-

ment. The two objects collide with each other only, if

the distance between their root sphere centers is equal

or less than the sum of their respective radius (See

Figure 6). When a collision occurs, one level is con-

structed for the OCST for objects A and B. If child

nodes of object A collide with child nodes of object B,

an additional level is constructed only for the collid-

ing child nodes. This process continues up to a user–

deﬁned depth for the OCST (in our experiments the

maximum depth level has been selected from: 5, 6

and 7). When the depth value is reached, and two leaf

nodes collide, a collision between object A and B is

reported. Using a bigger depth value, the approxima-

tion to the object surface is tighter, and the collision

detection is more accurate.

All hierarchies sphere centers must be updated with

the objects in movement. When a new level for the

OCST is created the number of updates increases.

With a big user–deﬁned depth value the maintaining

cost of updating all the animation OCSTs is higher.

To found the potentially colliding set, PCS, the sphere

interference test described below is used. A list with

pair–colliding spheres is computed and used to iden-

tify interfering object parts. In large environments

(Franquesa-Niub

o, 2004; Rodr

ıguez and Franquesa-

Niub

o, 005c), the PCS can be obtained using algo-

rithms designed for the broad phase of the hybrid col-

lision detection problem.

To increase the algorithm performance, the

branches of the OCST created by older collisions are

kept in core memory. These can be re-used on forth-

Figure 7: Two examples of input data models. Top: Cow

and Bunny modeled by triangle–soup, with 5144 and 5110

triangles respectively. Down: Same input objects modeled

by using triangle–strips.

coming collision tests. To avoid the problem of a high

computing resource cost caused for hierarchies up-

dates, a time-stamp is assigned to the deeper OCST

nodes. If a complete OCST level does not participate

in a collision during a certain amount of time, it is

deleted from core memory and the parent initialized

with its own time-stamp. This will cause an object to

get back to its initial state (only the OCST root node

is kept), if it is not involved in any more collisions

during a certain amount of time (This is the case of

the Cow and the Dragon of Figure 8).

6 EXPERIMENTAL RESULTS

In this section some relevant results of applying our

method are exposed. To compare the actual re-

sults with existing others, the input data tested in

other existing algorithms has been selected. Expla-

nations about simulations and results can be found

in (Rodr

ıguez and Franquesa-Niub

o, 005a). The al-

gorithms have been implemented on a Dell Inspiron

notebook with ATI Mobility Radeon 9600 graphics

card with 128 MB VRAM and a Pentium M proces-

sor at 1.80 GHz. The algorithms were tested with

commonly used complex models

. Figure 7 shows

the models used.

6.1 OCST Construction Timings

The time to construct one level of an OCST is ex-

posed in Table 1. This time is equal for the two

models used, triangle–soup and triangle–strips. The

results are obtained with the objects already loaded

in graphics card’s memory as triangles regardless of

with the kind of triangulation chosen, triangle–soup

http://isg.cs.tcd.ie/spheretree/

SPHERE–TREES GENERATION AS NEEDED IN REAL TIME

Table 1: OCST construction time.

Model Triangles Time Occlusion

Dragon 1496 0.0099 13

Bunny 1500 0.0099 9

Cow 1500 0.0099 9

Lamp 600 0.0199 13

Dragon 5104 0.0199 13

Bunny 5110 0.0099 9

Cow 5144 0.0099 9

or triangle–strip. The Table shows the number of tri-

angles for each model, the time used to construct the

level (in seconds) and the number of occlusion tests

performed.

The complete model has to be rendered for each oc-

clusion test. Note that the object’s geometry does not

affect the time of constructing one OCST new level.

The algorithm performance is affected only for the

number of occlusion tests and the time each one lasts.

Therefore, the worst case only occurs when all occlu-

sion tests have to be considered, for all the nodes and

axis. In this case, with eight possible child nodes and

three tests per each one, for a total of 24 occlusion

tests, the maximum experimented time has resulted

equal to 0.03 seconds. For the simplest model the

construction of an OCST level using only the CPU

can take from 0.03 seconds, 0.1 to 0.5 seconds for

the intermediate models, and 1 second or more for

the largest models. Without the use of the GPU for

the construction, the object’s geometry does indeed

affect the algorithm performance. The optimizations

such as triangle–strips have proved useful to accel-

erate the render of the complete model. Therefore,

using triangle–strips is faster for the OCST construc-

tion, as it is shown by the results in the next section.

6.2 OCST Collision Detection

Performance

The algorithms were tested with a scenario where one

object follows a ﬁxed trajectory in a 3D space. Col-

lision occurs among the other three objects. Figure 8

shows a snapshot of an example of collision simula-

tion: The initial location of the Bunny is B

. Then

following a trajectory, it passes through B

, B

, and

(place where the snaptshot has been taken). In B

the Bunny collided with the dragon, in B

the Bunny

collided with the Cow and in B

the Bunny is col-

liding with a lamp. While the collision is being de-

tected, new levels of the respective objects trees are

generated. When the collision is false, the tree is go-

ing up to the root node, deleting all the nodes. This

last reason is the key why the dragon and the cow are

sorrounded by big spheres, because the trees are go-

Figure 8: Example of a collision detection fragment anima-

tion: Snapshot where one object, the Bunny is moving and

the other three objects are still.

ing up. Table 2 and Table 3 show the performance for

the animation, and the time taken to ﬁnish it. The ta-

bles use triangle–soup and triangle–strip respectively

to render the models and represent the same anima-

tion. In the two situations, a user–deﬁned depth level

for the OCST equal to 5 is used. The results are mea-

sured in frames–per-second (FPS). The number of oc-

clusion queries performed in each time step is also

shown. Comparing the results exposed in the tables,

we can conclude that the use of triangle–strips is bet-

ter than the use of triangle–soups. Note for example

the number of frames per second at 4 sec. of the ani-

mation time, with 694 occlusion queries for triangle–

soup and 690 queries for triangle–strip and the FPS is

245.75 in the ﬁrst case and 297.70 in the second case.

Then the better ratio of FPS, indicates better results

for triangle–strips.

Looking at Table 2 and Table 3 and taking into ac-

count that the simulation trajectory was the same

in both cases, the time of the whole animation for

triangle–soup was equal to 8.582 sec, while for

triangle–strip was 7.360 sec.

FPS slowed down only, when new levels for the

OCSTs are generated. Although the speed of the

FPS gets lower, the rate keeps on being good enough.

Therefore, the animation can be maintained over 60

FPS and allows a smooth transition between frames

in visual terms.

The worst case occurs when objects are moving

very fast and a straight collision occurs. This situa-

tion can cause several levels of the OCST tree have

to be constructed at once for each colliding object. In

this case, the performance could slow down. Even so,

stalls in the animation can occur, only, if the user–

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

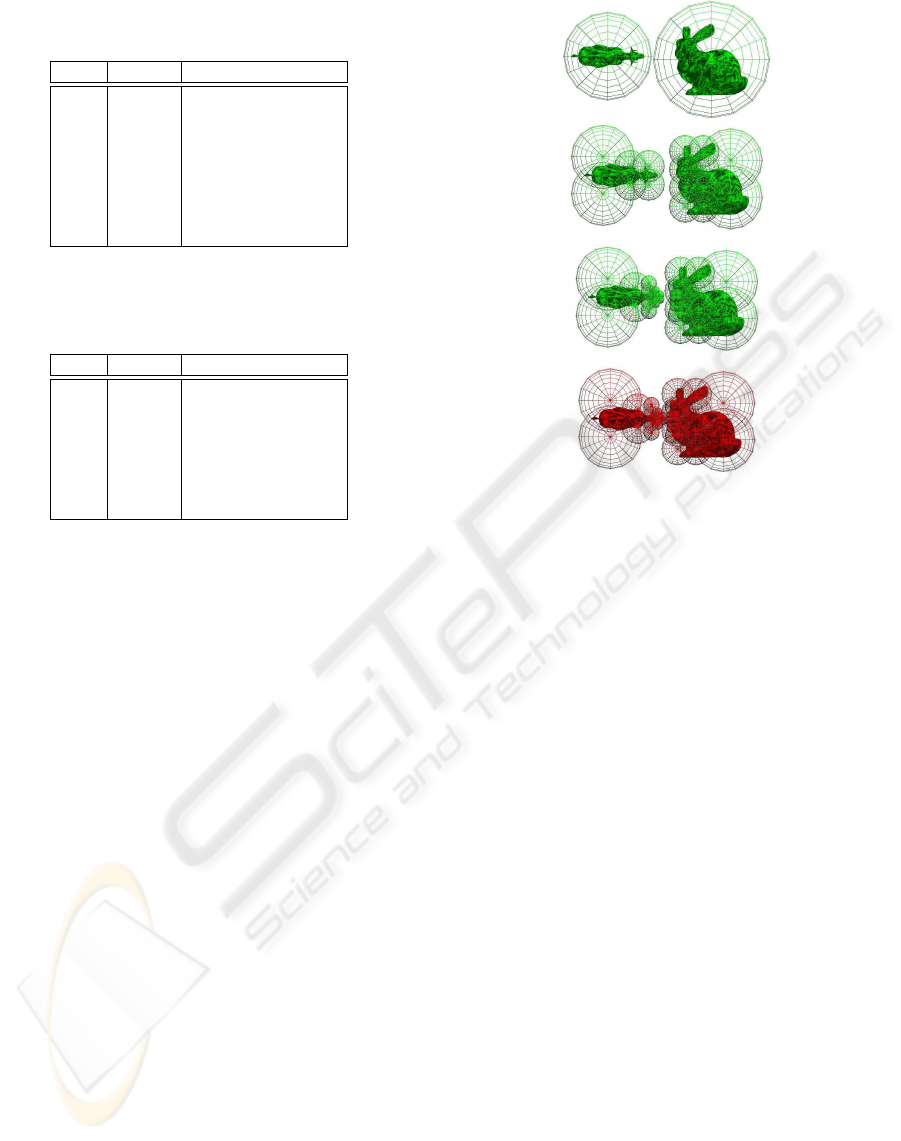
Table 2: Animation performance using triangle–soup mod-

els. Total animation time: 8.582 sec.

Time FPS Occlusion queries

1.00 177.64 198

2.00 244.76 700

3.00 274.45 316

4.00 245.75 694

5.00 264.47 490

6.00 283.72 294

7.00 294.71 182

8.00 268.46 754

Table 3: Animation performance using triangle–strip mod-

els. Total animation time: 7.360 sec.

Time FPS Occlusion queries

1.00 232.53 240

2.00 278.72 832

3.00 325.35 372

4.00 297.70 690

5.00 310.38 532

6.00 348.65 208

7.00 311.69 884

deﬁned depth value is too high. Even though, these

stalls are due to the high number of occlusion tests

that have to be performed to construct all the OCST

branches, the running time is not affected when real-

time simulations are computed.

Figure 9 shows the sequence of a collision between

two objects, modeled by using triangle–strips, with

the OCSTs created in real-time up to level 5. The red

colour indicates that a collision has been detected.

7 CONCLUSIONS

In this paper, two collision detection improvements

are described. Firstly, a new method that has been

conceived to speed up the collision detection pipeline

has been introduced. Its application in real-time en-

vironments has been implemented using OCST. The

method is fast enough to manage collision detection

in real-time, as it can be seen from the experimen-

tal results exposed. The speed and efﬁciency ob-

tained with our method enables us to manage many

concurrent objects in a scene. Secondly, we have

tested two kinds of triangulated models for the same

set of original objects: triangle–soup and triangle–

strip. Triangle–strip are shown to be better model in

terms of sphere–tree time computing. And, as a con-

sequence, they are better when computing collision

detection.

The method’s limitations are related to hardware

constrictions. The overall performance is affected

Figure 9: OCST creation up to level 5.

by several parameters. The amount and speed of

the video memory built–in the graphics cards, the

bus transfer speed and the clock frequency of the

GPU. Other existing methods that use out-of-core al-

gorithms in real-time could be degraded at reading

time from secondary storage, and at sending time of

the object’s geometry to the graphic card memory.

The amount of the model representation to be

generated is reduced with the use of OCST, while

decreasing considerably the collision detection time

without loss of accuracy.

We have detailed here, an algorithm related to the

narrow phase of the collision detection pipeline prob-

lem. However, work related to the broad phase can

be found in (Franquesa-Niub

o, 2004; Rodr

ıguez and

Franquesa-Niub

o, 005c). We are working on bringing

together both methods, so a fully functional fast col-

lision detection system for large environments could

give us better results on our application environments.

ACKNOWLEDGEMENTS

This research has been partially supported by the

projects MAT2002-0497-C03-02, MAT2005-07244-

C03-03, the network IM3 from the spanish govern-

ment, by the CREBEC, from the catalan government

and by the Facultad de Ingenier

ıa de la Universidad

Aut

onoma de San Luis Potos

ı under the PROMEP

program.

SPHERE–TREES GENERATION AS NEEDED IN REAL TIME

REFERENCES

Baciu, G. and Wonk, S. (1998). Recode: An image-

based collision detection algorithm. In Proc. of Paciﬁc

Graphics, pages 497–512.

Bradshaw, G. and OSullivan, C. (2003). Adaptative me-

dialaxis approximation for spheretree construction.

ACM Transactions on Graphics, 22(4).

Fan, Z., Wan, H., and Gao, S. (2004). Simple and rapid

collision detection using multiple viewing volumes. In

VRCAI 04: Proceedings of the 2004 ACM SIGGRAPH

international conference on Virtual Reality continuum

and its applications in industry, pages 95–99. ACM

Press.

Franquesa-Niub

o, M. (2004). Collision Detection in Large

Environments using Multiresolution KdTrees. PhD

thesis, Universitat Polit

ecnica de Catalunya.

Franquesa-Niub

o, M. and Brunet, P. (2003). Collision de-

tection using MKtrees. In Proc. CEIG 2003, pages

217–232.

Franquesa-Niub

o, M. and Brunet, P. (2004). Collision pre-

diction using MKtrees. In Scopigno, R. and Skala, V.,

editors, WSCG 2004, The 12th International Conf. in

Central Europe on Comp. Graphics, Visualization and

Comp. Vision 2004, volume 1, pages 63–70. Plzen.

ISSN 1213-6972.

Govindaraju, N. K., Redon, S., Lin, M. C., and Manocha,

D. (2003). Cullide: interactive collision detection be-

tween complex models in large environments using

graphics hardware. In HWWS 03: Proceedings of

the ACM SIGGRAPH/EUROGRAPHICS conference

on Graphics hardware, pages 25–32. Eurographics

Association.

Hubbard, P. M. (1993). Interactive collision detection. In

Proc. IEEE Symp. on Research Frontiers in Virtual

Reality, volume 1, pages 24–31.

Hubbard, P. M. (1995). Collision detection for interactive

graphics applications. IEEE Transactions on Visual-

ization and Computer Graphics, 1(3):218–230.

Hubbard, P. M. (1996). Aproximating polyhedra with

spheres for timecritical collision detection. ACM

Transactions on Graphics, 15(3):179–210.

Jimenez, P., Thomas, F., and Torras, C. (2001). (3d) colli-

sion detection: A survey. Computers and Graphics,

25(2):269–285.

Kim, Y. J., Otaduy, M. A., Lin, M. C., and Manocha, D.

(2003). Fast penetration depth estimation using ras-

terization hardware and hierarchical reﬁnement. In

SCG 03: Proceedings of the nineteenth annual sym-

posium on Computational geometry, pages 386–387.

ACM Press.

Kitamura, Y., Takemura, H., Ahuja, N., and Kishino, F.

(1994). Efﬁcient collision detection among objects in

arbitrary motion using multiple shape representation.

In Proceedings 12th IARP Inter. Conference on Pat-

tern Recognition, pages 390–396.

Kornmann, D. (1999). ”fast and simple triangle strip gener-

ation”. VMS Finland, Espoo, Finland. Color Plates.

Lin, M. and Manocha, D. (2003). Handbook of Discrete and

Computational Geometry Collision Detection, chap-

ter 35. CRC Press LLC. To appear.

Myszkowski, K., Okunev, O. G., and Kunii, T. L. (1995).

Fast collision detection between computer solids us-

ing rasterizing graphics hardware. The Visual Com-

puter, 11.

O’Sullivan, C. (1999). Perceptually-Adaptive Collision De-

tection for Real-time Computer Animation. PhD the-

sis, University of Dublin, Trinity College Department

of Computer Science.

O’Sullivan, C. and Dingliana, J. (1999). Real-time collision

detection and response using sphere-trees. In 15th

Spring Conference on Computer Graphics. ISBN: 80-

223-1357-2.

Palmer, I. and Grimsdale, R. (1995). Collision detection

for animation using sphere–trees. Computer Graphics

Forum.

Pobil, A. D., Serna, M., and Llovet, J. (1992). A

new representation for collision avoidance and detec-

tion. In IEEE Int. Conf. on Robotics and Automation

(Nice)(France), volume 1, pages 246–251.

Quinlan, S. (1994). Efﬁcient distance computation between

nonconvex objects. In Proceedings of the IEEE Int.

Conf. on Robotics and Automation, pages 3324–3329,

San Diego, CA.

Rodr

ıguez, O. and Franquesa-Niub

o, M. (2005a). A new

gpu based sphere-tree generation method to speed

up the collision detection pipeline. Technical report,

Software Dept. LSI. U.P.C. Ref: LSI-05-45-R. http:

//www.lsi.upc.edu/dept/techreps/techreps.html.

Rodr

ıguez, O. and Franquesa-Niub

o, M. (2005b). A new

sphere-Ttree generation method to speed up the colli-

sion detection pipeline. In Proceedings of CEIG’05,

September 2005. Granada. Spain.

Rodr

ıguez, O. and Franquesa-Niub

o, M. (2005c). Hierar-

chical structuring of scenes with MKTrees. Technical

report, Software Dept. LSI. U.P.C. Ref: LSI-05-4-R.

http://www.lsi.upc.edu/dept/techreps/techreps.html.

Rossignac, J., Megahed, A., and Schneider, B.-O. (1992).

Interactive inspection of solids: cross–sections and in-

terferences. In SIGGRAPH 92: Proceedings of the

19th annual conference on Computer graphics and in-

teractive techniques, pages 353–360. ACM Press.

Rourke, J. and Badler, N. (1979). Decomposition of three-

dimensional objects into spheres. IEEE Transactions

on Pattern Analysis and Machine Intelligence, PAMI-

1(3):295–305.

Samet, H. (1990). The Design and Analysis of Spatial Data

Structures. Addison–Wesley. ISBN 0–201–50255–0.

Shinya, M. and Forgue, M. (1991). Interference detection

through rasterization. Journal of Visualization and

Computer Animations, 2:131–134.

Vassilev, T., Spanlang, B., and Chrysanthou, Y. (2001).

Fast cloth animation on walking avatars. In Computer

Graphics Forum, volume 20(3), pages 260–267.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS