EMPOWERING ISO-SURFACES WITH VOLUME DATA

D.M. Eler, P.S.H. Cateriano, L.G. Nonato, M.C.F. de Oliveira

Universidade de S

ao Paulo

Instituto de Ci

encias Matem

aticas e de Computac¸

Av. Trabalhador S

ao-Carlense 400, POBox 668, 13560-970, Brasil

H. Levkowitz

Department of Computer Science

University of Massachusetts Lowell

Lowell, MA 01854, USA

Keywords:

Hybrid rendering, Iso-Surface rendering, Ray-Tracing, Volume on Surface.

Abstract:

Surface rendering (SR) algorithms are fast, but not suited to applications that demand exploration of internal

volume structures. We introduce an enhanced surface rendering algorithm - named VoS, Volume on Surface-

that supports visualization of internal volume structures. VoS integrates surface and volume rendering into an

efﬁcient framework for interactive visualization of volume information. A ray casting is performed to map

volume information onto a boundary surface extracted from the volume grid, enabling the display of structures

internal to the surface using conventional SR. VoS thus offers a low-cost alternative to volume rendering

in some practical situations, as its resulting surfaces can be rendered on commodity graphics hardware at

interactive rates. Moreover, changes in the transfer functions are handled at the rendering step, rather than at

the costly ray-casting operation.

1 INTRODUCTION

Volume visualization has enjoyed signiﬁcant evolu-

tion in recent years, contributing to major advances in

important applications. In medicine, for example, it

has played an essential role in the empowerment of

imaging technologies, such as ultra-sound, and in the

development of computer-guided surgery. It contin-

ues to play a major role in computer-assisted diagno-

sis, motivating further research into methods capable

of generating improved visualization of internal body

structures at faster rates.

Despite the availability of speciﬁc hardware and ef-

fective algorithms, volume visualization is still slow

and computationally expensive as compared to sur-

face rendering. It is not an option if the goal is fast

image generation on standard graphics cards. Surface

rendering is fast, but has limited applicability. Con-

ventional surface rendering approaches completely

dismiss the volumetric information, and therefore, are

not suited to applications that demand exploration of

internal volume structures.

We introduce an enhanced surface rendering al-

gorithm – named VoS, Volume on Surface – that

supports visualization of internal volume structures.

VoS integrates surface and volume rendering into an

efﬁcient framework for interactive visualization on

standard graphics cards. A pre-processing step uses

ray casting to map the volumetric domain grid infor-

mation onto a boundary surface extracted from this

grid, enabling the display of structures internal to

the surface using conventional surface rendering. As

such, the technique exploits the advantages of surface

rendering while keeping the volumetric information.

VoS thus offers a low-cost alternative to volume ren-

dering in some practical situations, as its resulting sur-

faces can be rendered on commodity graphics hard-

ware at interactive rates. Moreover, changes in the

color and opacity transfer functions are handled at the

rendering step, with no need to repeat the costly ray-

casting operation.

This paper is organized as follows: Section 2

presents an overview of related work. Section 3 de-

scribes the VoS algorithm, and some results of its ap-

plication to visualizing volume data are presented and

discussed in Section 4. Final remarks and plans for

further work are presented in Section 5.

2 RELATED WORK

Many volume visualization techniques have been pre-

sented in the literature over the last years, making

it difﬁcult to accomplish a fair short overview. We

372

M. Eler D., S.H. Cateriano P., G. Nonato L., C.F. de Oliveira M. and Levkowitz H. (2006).

EMPOWERING ISO-SURFACES WITH VOLUME DATA.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 372-377

DOI: 10.5220/0001356503720377

 SciTePress

restrain ourselves to brieﬂy introducing the two ma-

jor approaches adopted by volume visualization tech-

niques, namely, Surface Rendering (SR) and Direct

Volume Rendering (DVR). Concerning speciﬁc tech-

niques, we emphasize a third class of so-called Hy-

brid algorithms, which, similarly to our proposed ap-

proach, combine SR and DVR to make up a visual-

ization framework.

Surface Rendering techniques adopt the gen-

eral approach of extracting from the volume two-

dimensional geometric entities of interest, which

are then displayed with conventional SR algo-

rithms (Lorensen and Cline, 1987; Nonato et al.,

2001; Marmitt et al., 2004). In contrast to SR, Di-

rect Volume Rendering techniques do not extract any

geometric representation in the visualization process,

handling the volumetric data in a direct way (Levoy,

1990a; Westover, 1990). Although lower computa-

tional cost has initially motivated the adoption of SR

methods in a wide range of applications, recent de-

velopments in DVR have put in check such an advan-

tage (Wald et al., 2005). The ability to provide high-

quality images of three-dimensional internal struc-

tures at reasonable interactive rates and acceptable

costs stimulates the choice of DVR as a volume visu-

alization approach, particularly in critical ﬁelds such

as medicine and biology. However, good solutions re-

quire top-of-the-line graphics cards.

Techniques that integrate different types of

processing into a single visualization strategy are usu-

ally called hybrid volume rendering techniques. The

term “hybrid rendering”, however, has been employed

in different contexts. One such context refers to a

wide class of algorithms characterized by combin-

ing SR and DVR strategies into a single visualiza-

tion environment. Examples include combining SR

with ray-tracing (Levoy, 1990b) or splatting (Tost

et al., 1993). Such approaches enable simultaneous

visualization of volumetric data and objects modeled

from geometric primitives. A typical application is

computer-aided surgery, where surgical instruments

must be surface rendered while patient’s data is shown

with DVR (Gross, 1998). Other hybrid approaches,

such as the one by (Zakaria and Saman, 1999), in-

tegrate SR, DVR and domain transform into a single

environment.

Another use of the term refers to Image-Based Hy-

brid Rendering techniques, which map a set of images

generated from a volume onto surfaces that can then

be rendered on conventional graphics hardware (Wil-

son et al., 2002). The mapping is typically performed

using texture maps available in graphics cards. Chen

et al.’s work (Chen et al., 2001) is a good represen-

tative of this class. In their method, the main idea

is to pre-compute, using conventional DVR, a set of

keyviews, which, depending on the viewer’s position,

are texture-mapped onto a surface that bounds the vol-

ume of interest (their solution uses a sphere as the

bounding surface). When a viewer moves away from

a keyview, the texture is kept in the regions still visible

and rays are cast for pixels in newly visible regions.

An important issue is where to place the cameras to

generate the keyviews. Another problem is that un-

desired holes appear in the image when the viewer

moves away from the keyviews.

(Samanta et al., 2000) name as “hybrid” a par-

allel volume visualization algorithm that sub-divides

both the volumetric and the image domains in or-

der to improve processor load balance. Sometimes

the term is also employed to describe optimization

approaches introduced in traditional rendering algo-

rithms. Levoy and Whitaker’s (Levoy and Whitaker,

1990) and Laur and Hanrahan’s (Laur and Hanra-

ham, 1991), for example, are considered hybrid ap-

proaches, though they are essentially DVR algorithms

highly optimized through progressive mesh reﬁne-

ment and hierarchical representations.

Our technique also combines SR and ray casting

into a uniﬁed algorithm. However, its goal is not

to enable simultaneous visualization of geometrically

deﬁned surface models and volume data. Ray-casting

is used as a mechanism to enrich the surface rendering

with volume information, in an approach that bears

similarity with image-based approaches such as the

one by (Chen et al., 2001). However, some differ-

ences are distinguishable:

1) the volumetric information is transferred to a

user-speciﬁed iso-surface extracted from the data vol-

ume, rather than to an external surface bounding

the volume; 2) VoS uses no texture mapping, i.e.,

rays are cast directly from the faces of the bound-

ary surface; 3) ray casting is executed only in a pre-

processing step; 4) changes in the color and opacity

transfer functions are handled in the rendering step,

with no need to redo the ray casting; 5) VoS presents

no problems with camera positions.

VoS can be summarized as follows: given a vol-

ume stored in a regular grid of voxels, a ray-casting al-

gorithm maps the volumetric information onto a sur-

face of interest extracted from the volume. Note that

only content internal to the extracted surface will be

shown. A SR algorithm is then applied to produce a

volumetric visualization of the domain.

3 THE VoS TECHNIQUE

Given a regular volume grid, a surface of interest must

be extracted. Iso-surface geometry and other infor-

mation required by the mapping process are stored

in a topological data structure. A high-pass ﬁlter is

applied to the volume and the resulting information

is also stored to allow identifying transitions between

EMPOWERING ISO-SURFACES WITH VOLUME DATA

373

materials. Let S be the input iso-surface, f be a face

of S and P be the plane containing f, as shown in Fig-

ure 1. Face f can be seen from any point P on the op-

posite side of S (as in Figure 1 (a)). If S is a transpar-

ent object, part of its internal volume will be observ-

able through f . Depending on the viewer’s position,

different internal structures can be observed through

f. Evidently, the pattern of colors (or ’texture’) ob-

servable will change as the viewpoint changes.

b)a)

Figure 1: a) Viewing region of f; b) Sampling the viewing

directions of f. The bold arrows illustrate the observation

line that best approximates the viewing direction.

If one could compute and store the texture of f for

every possible viewing direction it would be possible

to identify and assign the appropriate texture to f for

any viewpoint. Therefore, a viewer would be able to

observe any structures contained in S processing only

the surface representation. Obviously, it is not feasi-

ble to compute or even store the colors of the ver-

tices for all possible viewing positions and directions.

Thus, VoS samples a sub-set of all possible viewing

directions from which one might observe the interior

of S through the vertices of f. The sampled viewing

directions are called ’observation lines’.

For each face f the algorithm computes, for each

observation line, the colors that approximate the tex-

tures in the face when observed from that particular

direction. In fact, colors are pre-computed and stored

at the vertices, and the color of a face is computed in

the rendering step. When computing face colors the

rendering algorithm will identify, for each face ver-

tex, which of the pre-computed observation lines best

approximates the viewer’s line of sight for that vertex.

It then assigns to the face a color computed from the

average of the colors assigned to its vertices, as illus-

trated in Figure 1 (b). Finally, the rendering algorithm

just renders all visible faces.

The technique is thus a two-step method: (i) Pre-

visualization (maps the volume onto the extracted sur-

face); and (ii) Surface rendering (renders and projects

the surface). In the following we describe both steps

in detail and discuss some implementation issues.

3.1 Pre-visualization

Pre-visualization, responsible for the ray-casting

process, concentrates the core of the processing. This

step takes as input a volume grid of voxels and an iso-

surface extracted from it.

3.1.1 Sampling the Viewing Directions

To sample the set of all possible viewing directions

and deﬁne a set of observation lines for each sur-

face vertex, VoS deﬁnes virtual cones with differ-

ent opening angles, centered at the vertex and aligned

with its normal vector, as illustrated in Figure 2. The

observation lines start from the vertex and have their

directions determined by uniformly distributing them

over the surface of each cone (Figure 2). VoS current

implementation uses, for each vertex, a set of cones

with equally spaced opening angles. For example, if

three cones are used they have opening angles equal

to 15

, 45

and 75

from the vertex normal vector;

if four observation lines are cast, the angle between

each two of them is 90

, measured on the cone.

Figure 2: Three virtual cones with different opening angles

and observation lines deﬁning the viewing directions to be

sampled.

3.1.2 Storing Samples

This step involves casting rays through the volume

in the directions of the observation lines, similarly

to traditional Ray Casting. Discrete ray trajectories

are computed with a 3D scanline algorithm. Each

voxel along the scanline whose value after applying

the high-pass ﬁlter is within a user-speciﬁed threshold

is stored as a ray sample. Each ray is thus associated

with a list of its stored samples.

3.1.3 Transfer Function Speciﬁcation

User deﬁned transfer functions are responsible for

computing the color and opacity associated with ray

samples. VoS currently offers a simple interface for

intensity-based color transfer function deﬁnition, and

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

374

two alternative types of opacity transfer functions,

one based on intensity and one based on the sample’s

spatial position along the ray. The rationale for the

latter option is that samples positioned closer to the

extreme ends of the ray (its starting point or its ﬁ-

nal intersection point) correspond to ray intersections

with the most external or the most internal objects in

the volume. A user can then assign opacity values

based on sample position, as exempliﬁed in Figure

3, which shows two rays and their associated sam-

ple points (represented by the squares). To favor vi-

sualization of internal structures one assigns higher

opacity values to samples in the internal regions of

the ray, as shown in Figure 3 (a). On the other hand,

to highlight more external object structures one as-

signs higher opacities to the samples closer to the ray

extremes, as illustrated in 3 (b).

a) b)

Figure 3: a) Opacity function to highlight internal struc-

tures; b) Opacity function to highlight object borders.

3.1.4 Color Computation

The samples stored on a given ray are composed to

determine the ray color and opacity values. We adopt

the simple optical model proposed by Levoy (Levoy,

1990a), stated as follows:

C =

i=1

c(i)α(i)

j=1

(1 − α(j))

In the above equation C is the ﬁnal color and N

is the number of samples. c(i) and α(i) represent,

respectively, color and opacity of sample i and α(j)

represents opacity of sample j. Each surface vertex

stores the values of C computed for each ray cast from

it. If the color or opacity functions are modiﬁed a

new composition must be performed, but no further

ray casting is required.

3.2 Surface Rendering

At the end of the pre-visualization step a ﬁnal color

has already been assigned and stored for each ray (ob-

servation line) leaving each surface vertex. The ini-

tial problem for the rendering stage is to decide the

appropriate color for the vertex as observed from the

viewer’s current position.

The problem may be solved with a dot prod-

uct computation: Let v be the vertex and R =

, . . . , r

} (k = number of cones * number of rays

cast per cone) the set of unit vectors on the obser-

vation lines (pointing outwards from S). Let r

the unit vector constructed from the viewer position,

O, to the vertex. Suppose that r

points towards the

viewer and r

is the vector in R whose dot product

· r

produces the largest positive value. The color

associated with observation line r

is thus attributed to

v as the most appropriate color for v when observed

from O. This dot product computation can be per-

formed in hardware, and the same happens for the

computation of hidden elements and light effects on

the surface. These operations are supported by a con-

siderable number of commodity graphics cards, en-

suring the efﬁciency of the rendering step.

4 RESULTS

In this section we present some results of applying

VoS to visualize internal volume structures. All vi-

sualizations in this Section were produced on a Pen-

tium 4, CPU 3.2 GHz with 1 GB RAM.

Figure 4 shows two visualizations of a chest

data set (http://www9.cs.fau.de/Persons/Roettger/library/),

with dimensions 120x120x241. The visualiza-

tion in Figure 4 (a) was generated with Kitware’s

Volview (http://www.volview.com) using conven-

tional ray casting. Figure 4 (b) shows a shaded sur-

face rendering of the same data, for an isosurface

value of 80, created with VTK’s vtkContourFilter

method (Schroeder et al., 2004). The resulting mesh

has 83,949 vertices and 167,241 faces. The VolView

visualization took nearly 20 seconds to compute; iso-

surface visualizations have a rate of nearly 2 frames

per second on VTK.

Figure 4: a) Ray casting image; b) Surface rendering image

with isosurface = 80.

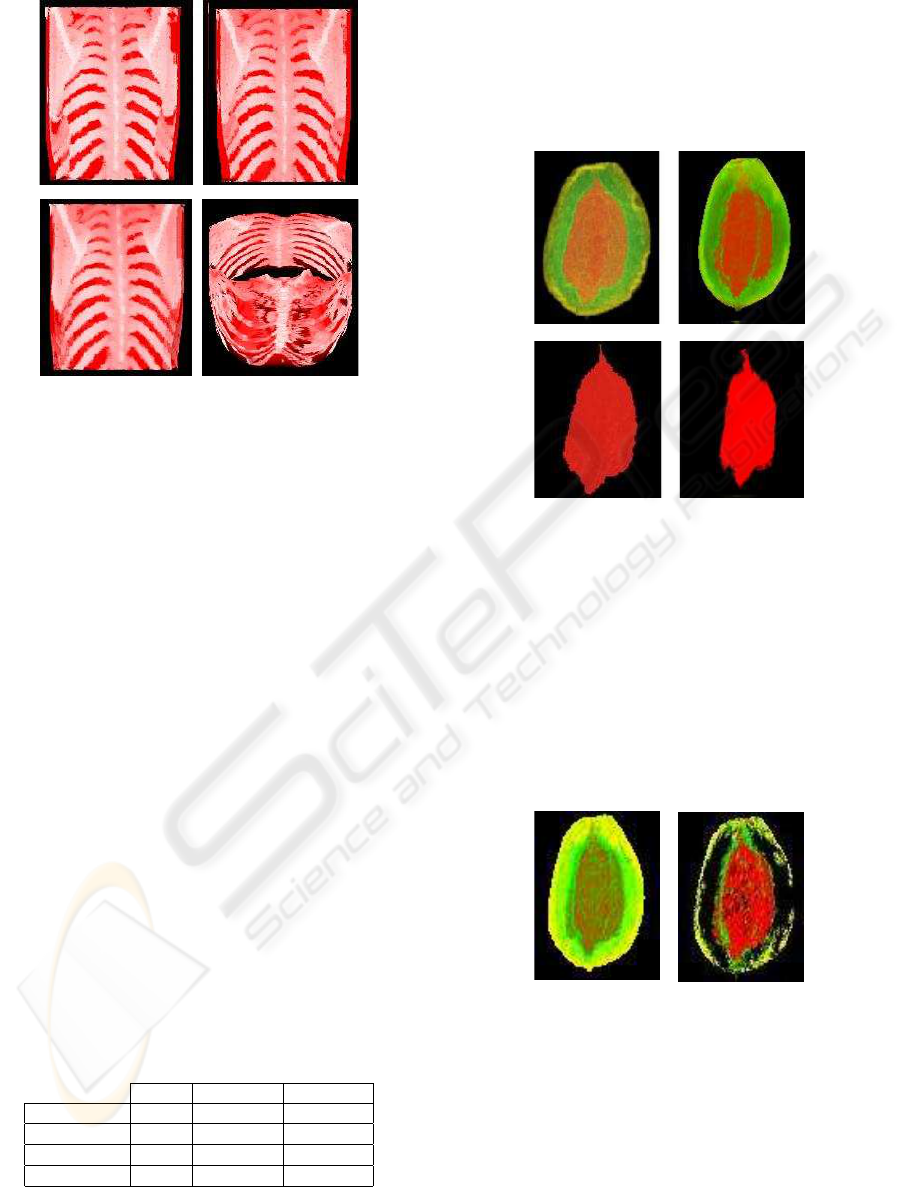
Figure 5 shows VoS visualizations of the same

data. Figures 5 (a)-(c) were created with 3, 6 and 8

cones per vertex, respectively, casting 8 observation

lines per cone. The quality of the VoS visualizations

is comparable to that of the ray casting image shown

in Figure 4 (a), even for the one generated with less

cones.

EMPOWERING ISO-SURFACES WITH VOLUME DATA

375

Figure 5: VoS visualizations using 8 observation lines per

cone a) three cones; b) 6 cones; c) 8 cones; d) 8 cones, from

a different viewpoint.

Computational times are shown in Table 1. Pre-

visualization time is the time to cast all rays from

all surface vertices and store their associated sam-

ples. The best and worst case entries indicate the

time to re-compute color composition when transfer

functions are modiﬁed. In the best case all scalar val-

ues are associated with the maximum opacity value,

and therefore ray casting stops at the ﬁrst sample;

in the worst case all samples along the ray must be

color-composed. The time to update the visualization

once the transfer functions change is much shorter

than in conventional ray casting, as the pre-processing

step stores all the necessary information, avoiding

the need of re-casting rays. Also, the number of

frames rendered per second with VoS is lower than,

but on the same order of magnitude, that of a con-

ventional SR implementation. VoS pre-visualization

time is slightly greater than that of a DVR visualiza-

tion, when using 3 cones with 8 observation lines.

This time increases with the number of cones, how-

ever, once pre-processing is done surface renderings

can be displayed in much lower times, as shown in

Table 1.

Table 1: VoS measurements.

3x8 6x8 8x8

Pre-vis 41s 1min 36s 2min 10s

Best Case 0.25s 0.49s 0.64s

Worst Case 2.3s 3.85s 4.88s

fps 1.9 1.3 1.1

Figure 6 shows another comparison between visu-

alizations created with conventional ray casting and

with VoS, now for a papaya fruit data set, with dimen-

sions 86x42x59. This example reinforces that VoS

can be a reasonable alternative to conventional DVR

in some applications, with the advantage of allowing

more interactive display rates. Figure 7 was created

Figure 6: Papaya data set: (a) and (c) Conventional ray-

casting; (b) and (d) VoS (8 cones with 8 observation lines).

with VoS and the opacity function based on sample

position. The visualization shown in Figure 7 (a), ob-

tained with the opacity function depicted in Figure 8

(a), shows the outer parts and the pulp that hides the

seeds. The internal hole is highlighted in Figure 7(b),

obtained conﬁguring the opacity function as shown in

Figure 8 (b). Memory usage requirements depend

Figure 7: a) Minimum (0) and maximum (1) opacity at the

ends of the ray; b) Maximum opacity between positions

[0.39, 0.47] and [0.53, 0.64].

on three factors: the number of surface vertices, the

number of observation lines cast per vertex, and the

number of samples stored for each observation line.

For the VoS visualizations of the papaya data set in

Figures 6(b) and (d) (8 cones per vertex and 8 lines

per cone), memory consumption was close to 32 MB.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

376

a)0 1

opacity

ray samples

0.39

0.47 0.53 0.64

opacity

ray samples

Figure 8: Opacity transfer functions for Figure 7.

5 CONCLUSIONS

In this paper we introduced VoS, an image-based

surface rendering approach that supports fast visu-

alization of internal volume structures. VoS maps

the volume information contained within a surface

on its faces and enables efﬁcient rendering by pre-

computing and storing the information required at the

rendering step. A user still has the ﬂexibility of mod-

ifying the transfer functions in the rendering step in

order to hide or highlight information.

VoS has a major advantage in its ability to im-

age internal volume contents quickly on conventional

graphics hardware, thus offering enhanced surface

rendering. It provides an additional tool in situations

in which surface rendering is a natural visualization

solution. Moreover, it can be an alternative to quickly

generate initial views of volume contents, or to en-

able volume visualizations on devices where speciﬁc

volume graphics hardware is not available, such as

’portable’ devices.

One aspect that deserves further investigation is

how the quality of the resulting visualizations is af-

fected by the quality of the surface mesh. Mesh sim-

pliﬁcation and smoothing algorithms could be applied

prior to generating the visualizations, and their ef-

fect on the quality of the VoS outcome must be an-

alyzed. Further investigations shall also handle the

use of GPUs to speed up computations and using par-

allelism in the pre-processing and rendering stages.

Also, improved mechanisms for specifying color and

opacity transfer functions must be investigated.

ACKNOWLEDGMENTS

The papaya data has been provided by EMBRAPA,

Brasil. FAPESP (03/02815-0, 04/01756-2) and

CNPq (300531/99-0, 521931/95-5) have sponsored

this work. Haim Levkowitz was a Fulbright US

Scholar to Brazil (August 2004 - January 2005).

REFERENCES

Chen, B., Kaufman, A., and Tang, Q. (2001). Image-based

rendering of surfaces from volume data. In IEEE

Workshop on Volume Graphics, pages 355–358, Stony

Brook, NY, USA.

Gross, M. (1998). Computer graphics in medicine: From vi-

sualization to surgery simulation. ACM SIGGRAPH,

1(32):53–56.

Laur, D. and Hanraham, P. (1991). Hierarchical splatting:

A progressive reﬁnement algorithm for volume ren-

dering. Computer Graphics, 4(25):285–288.

Levoy, M. (1990a). A hybrid ray tracer for rendering poly-

gon and volume data. IEEE Computer Graphics and

Applications, 10(2):33–40.

Levoy, M. (1990b). Ray tracing of volume data. Vol-

ume Visualization Algorithms and Architectures (SIG-

GRAPH90), pages 120–147.

Levoy, M. and Whitaker, R. (1990). Gaze-directed volume

rendering. Computer Graphics, 2(24):217–223.

Lorensen, W. E. and Cline, H. (1987). Marching cubes:

la high resolution 3d surface construction algorithm.

Computer Graphics (Proc. SIGGRAPH), pages 163–

169.

Marmitt, G., Kleer, A., Wald, I., Friedrich, H., and

Slusallek, P. (2004). Fast and accurate ray-voxel in-

tersection techniques for iso-surface ray tracing. In

Proceedings of Vision, Modeling, and Visualization

(VMV), pages 429–435, Stanford, CA., USA.

Nonato, L., Minghim, R., Oliveira, M., and Tavares, G.

(2001). A novel approach for delaunay 3d reconstruc-

tion with a comparative analysis in the light of appli-

cations. Computer Graphics Forum, 20(2):161–174.

Samanta, R., Funkhouser, T., Li, K., and Singh, P. (2000).

Hybrid sort-ﬁrst and sort-last parallel rendering with a

cluster of pc’s. SIGGRAPH/EUROGRAPHICS Work-

shop in Graphics Hardware.

Schroeder, W., Martin, K., and Lorensen, B. (2004). The

Visualization Toolkit: An Object-Oriented Approach

to 3D Graphics. Kitware, 3 edition.

Tost, D., Puig, A., and Navazo, I. (1993). Visualization of

mixed scenes based on volume and surfaces. Fourth

Eurographics Workshop on Rendering, pages 281–

293.

Wald, I., Friedrich, H., Marmitt, G., and Seidel, H.-P.

(2005). Faster isosurface ray tracing using implicit kd-

trees. IEEE Transactions on Visualization and Com-

puter Graphics, 11(5):562–572.

Westover, L. (1990). Footprint evaluation for volume ren-

dering. Computer Graphics, 4(24):367–376.

Wilson, B., Ma, K.-L., and McCormick, P. S. (2002). A

hardware-assisted hybrid rendering technique for in-

teractive volume visualization. In VVS ’02: Proceed-

ings of the 2002 IEEE symposium on Volume visual-

ization and graphics, pages 123–130. IEEE Press.

Zakaria, M. and Saman, M. (1999). Hybrid shear-warp ren-

dering. Proceedings of the ICVC.

EMPOWERING ISO-SURFACES WITH VOLUME DATA

377