PROGRESSIVE TRANSMISSION AND RENDERING OF FOVEATED

VOLUME DATA

Chen Chen, Zhiyong Huang, Hang Yu, Ee-Chien Chang

Department of Computer Science, School of Computing

National University of Singapore, Singapore 117543

Keywords:

Progressive Transmission and Volume Rendering, Wavelet Foveation, Multiresolution.

Abstract:

With development of biomedical and networking technology, interactive volume rendering with data trans-

mitted via the network becomes an interesting topic. Two technical problems are data transmission and fast

volume rendering. In this paper, two schemes using Wavelet foveation are proposed and implemented: the

region-based and coarse-to-ﬁne. The ﬁrst scheme transmits and renders the region of interest (ROI) of volume

data on the client site at highest resolution for the ﬁrst time, and consequently it iteratively expands the region

layer by layer towards to the peripheral. While the second one gives a complete image in a low resolution for

the ﬁrst time on the client. The detail coefﬁcients will be transmitted continuously and the rendering result

will be progressively reﬁned depending on the distance to the ROI.

1 INTRODUCTION

Modern scanners such as CT and MRI provide de-

tailed cross-sections of objects at a very high resolu-

tion. These data sets occupy huge amount of memory

space. Some super computer centers maintain large

data repositories on servers whose data sets will be ac-

cessed through networks and rendered on clients for

researchers around the world to collaborate in their

research (Hancock and Hubbold, 1997) (Bhaniramka

and Demange, 2002).

The network’s bandwidth is relatively low for the

large scientiﬁc data sets. Lossy compression is typi-

cally employed to reduce data size. However, for very

large data sets, such reduction is still insufﬁcient, es-

pecially when interactivity is required. Region of in-

terest (ROI) is another approach to further reduce the

data size. The ROI is determined from the user’s in-

tention, which in turns prioritizes the data transmis-

sion. Hence, a few design issues are on how to trans-

late the user’s interactive feedback to the transmission

order of the data, and how to render and present the

partial information received in the client’s side. The

above design issues are the focus of this paper.

Many state-of-the-art lossy image compression

schemes are based on Wavelet transform. For natural

images and many medical volume data sets, a large

number of their Wavelet coefﬁcients have small val-

ues. The lossy compression is obtained by discarding

coefﬁcients lower than a threshold, and such thresh-

old determines the quality and compression rate. To

compress with ROI, different thresholds are set for co-

efﬁcients correspond to different spatial location. A

foveated volume can be viewed as a volume with mul-

tiple levels of ROI. The spatial resolution is highest at

a location known as fovea, but decrease gradually for

as the distance from the fovea increases.

We adopt the following approach of interactive

transmission and rendering. The Wavelet coefﬁcients

are progressively transmitted by the server and pro-

gressively rendered by the client, in an order deter-

mined by the location of the fovea indicated by the

user. There are two ways of progressive transmis-

sion/rendering. One is region-based, that is, the pri-

ority of an coefﬁcient will be inversely proportional

to its distance to the center fovea. The center fovea

will have the highest priority thus will be transmit-

ted and rendered ﬁrst on client site with highest res-

olution. The user on the client site will see a small

portion of the volume which he/she is most interested

in. It will then be expanded progressively until the

whole foveated volume is received (Figures 11 and

13). The other one is coarse-to-ﬁne scheme. The vol-

ume in lowest resolution will be transmitted and ren-

dered ﬁrst. More coefﬁcients will arrive successively

to reﬁne region near the fovea Thus, the user will ﬁrst

Chen C., Huang Z., Yu H. and Chang E. (2006).

PROGRESSIVE TRANSMISSION AND RENDERING OF FOVEATED VOLUME DATA.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 67-75

DOI: 10.5220/0001357400670075

 SciTePress

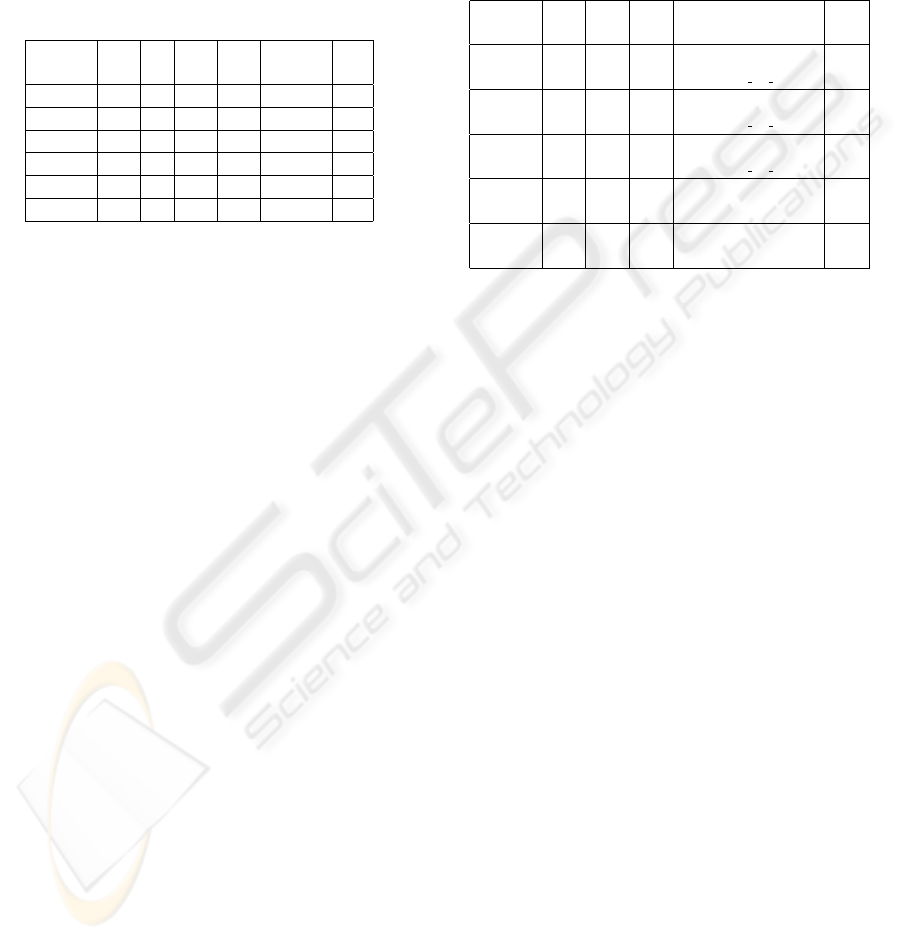
Table 1: Comparison of various data preprocessing meth-

ods: 1(Lacroute and Levoy, 1994), 2(Gross et al., 1997),

3(Ihm and Park, 1998), 4(Kim and Shin, 1999), 5(Guthe

et al., 2002), 6(Norton and Rockwood, 2003) (Wavelet-

Based (WB): y-yes, n-no. Output (O): 1-a list of voxel scan-

line, 2-the whole data set, 3-the signiﬁcant and near cubes,

4-the coefﬁcients of the visible frontal cubes; Data Access

(DA): 1-sequential, 2-random, 3-hierarchical; Compression

Rate (CR): –not applicable, l-low, m-medium, h-high; Re-

construction of a Single Voxel (RSV); Progressive Reﬁne-

ment (PR): y-yes, n-no).

Methods RB O DA CR RSV PR

1 n 1 1 - - n

2 y 2 2 m O(n) n

3 y 2 2 m O(1) n

4 y 2 2 h O(1) n

5 y 3 3 h O(log n) n

6 y 4 3 m O(log n) y

see a low resolution image, and next an image with

2 levels of details, follow by 3 levels of details and

so forth (Figures 12 and 14). We have implemented

the above two transmission/rendering schemes. The

results are compared and reported.

2 RELATED WORK

The huge amount of data is the most signiﬁcant prob-

lem both in data transmission and volume rendering.

The technical solution includes data compression and

fast volume rendering.

Many researchers employed Wavelet transform in

their compression schemes for volume rendering.

They usually contain four steps: Wavelet transform,

normalization, thresholding, and encoding. First,

transform the data into Wavelet domain. Second,

the Wavelet coefﬁcients are normalized to the inter-

val [0,1]. Third, those coefﬁcients that are smaller

than a certain threshold value are discarded. Fourth,

the data are encoded using some coding schemes like

run-length or Huffman. Data extraction is employed

further to extract the most important data and trans-

fer with priority for rendering. A comparison of some

compression methods is listed in Table 1.

There are four techniques that are particular pop-

ular in volume rendering: raycasting, splatting,

shear-warp and texture-mapping hardware-based ap-

proaches (Meissner et al., 2000). Raycasting and

splatting give better image quality but have lower ren-

dering speed. Raycasting casts a ray for each im-

age pixel into the volume and accumulate the sam-

ple value along the ray by resampling. In contrast

with ray casting, splatting, ﬁrst proposed in (West-

Table 2: Comparison of various rendering methods: 1(Pin-

namaneni et al., 2002), 2(Pinnamaneni, 2003), 3(Guthe

et al., 2002), 4(Lacroute and Levoy, 1994), 5(Kim and

Shin, 1999) (Output Resolution (OR): u-uniform, m-

multiresolution; Output Quality (OQ): l-low, m-medium, h-

high; Rendering Algorithm (RA): 1-2D texture mapping, 2-

3D texture mapping, 3-shear-warp; Rendering Time Com-

plexity (RTC); Rendering Space Complexity (RSC): l-low,

m-medium, h-high).

Methods OR OQ RA RS MC

1 u l 1 3 ∗ n(slice) m

∗n(voxel in slice)

2 u m 2 n(slice) h

∗n(voxel in slice)

3 m m 2 n(slice) l

∗n(voxel in slice)

4 u h 3 n(v o xel)− h

n(transparent)

5 u h 3 n(v oxel) m

−n(transparent)

over, 1990), is a feed forward algorithm calculating

the footprint which is the weight of the voxel con-

tributing to its neighboring pixel. Both methods have

been combined with Wavelet transform in order to re-

duce the size of volume data to ﬁt into core memory

(Westenberg and Roerdink, 2000) (Gross et al., 1997).

Texture-mapping is a hardware based method

which is very fast but gives lower image quality.

When the data set is too large that the texture is hard

to be loaded totally into texture memory, texture swap

will occur and rendering speed will reduce dramati-

cally. Shear-warp (Lacroute and Levoy, 1994) is the

fastest software-based algorithm and gives similar im-

age quality with raycasting and splatting. However,

when the magniﬁcation is high, signiﬁcant aliasing is

present. A comparison of some methods is listed in

Table 2. The image quality has been signiﬁcantly im-

proved in (Engel et al., 2001).

3 OUR WORK

Our method contains three steps: data preprocessing,

progressive transmission and progressive volume ren-

dering.

Volume data is ﬁrst transformed to Wavelet form

and divided into 8x8x8 blocks, each block is en-

coded using RLE (run-length encoding) in server site.

Blockwise structure is employed in order to enable

efﬁcient data compression as well as convenient com-

munication between server and client. When a client

request is received, a compressed foveated volume is

extracted. A foveated volume has highest resolution

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

at the fovea while the resolution falls off when the

distance with the fovea increases. We use Wavelet

foveation to approximate foveation operator (Chang

et al., 2000). For an original data set with size 1024

and fovea size 48

, the Wavelet foveated volume will

have approximately 24

∗ 36 = 497664 coefﬁcients,

which is reduced by a factor of 2,000 comparing with

the original size. Details of Wavelet transform and ex-

traction of foveated volume will be described in sub-

sections 3.1.1 and 3.1.2.

Data is then progressively transmitted in se-

quence. Data blocks of the Wavelet foveated volume

are reordered according to two priority assignment

schemes: region-based and the coarse-to-ﬁne. They

will be discussed in detail in subsection 3.2.

To be consistent with progressive data transmis-

sion, progressive rendering algorithm is employed. In

region-based scheme, the volume are displayed on

client site layer by layer from fovea toward the pe-

ripheral. The fovea area will be rendered in high res-

olution using data received earlier and in each suc-

cessive step, one immediate outer layer is displayed

in half resolution of its inner layer. In coarse-to-

ﬁne scheme, the client will ﬁrst show a rough aver-

age image of the volume and iteratively reﬁnes the

fovea area. Two progressive rendering algorithms are

described in subsection 3.3.1. Viewing from a non-

orthogonal direction will be discussed in subsection

3.3.2.

3.1 Data Preprocessing

3.1.1 Data Compression

Haar Wavelet is implemented because it is simple and

has a good correspondence with octree that enables

easy data searching and reconstruction.

Haar Wavelet transform We will illustrate it in 2D

case ﬁrst. Let I be an image of size 2

× 2

. Four

images can be generated from I after one pass of Haar

Wavelet transform, where

(i, j)=

I(2i, 2j)+I

(i, j)+I

(i, j)

(i, j)=I(2i +1, 2j)

(i, j)=I(2i, 2j +1)

(i, j)=I(2i +1, 2j +1)

i, j =0...2

N −1

− 1

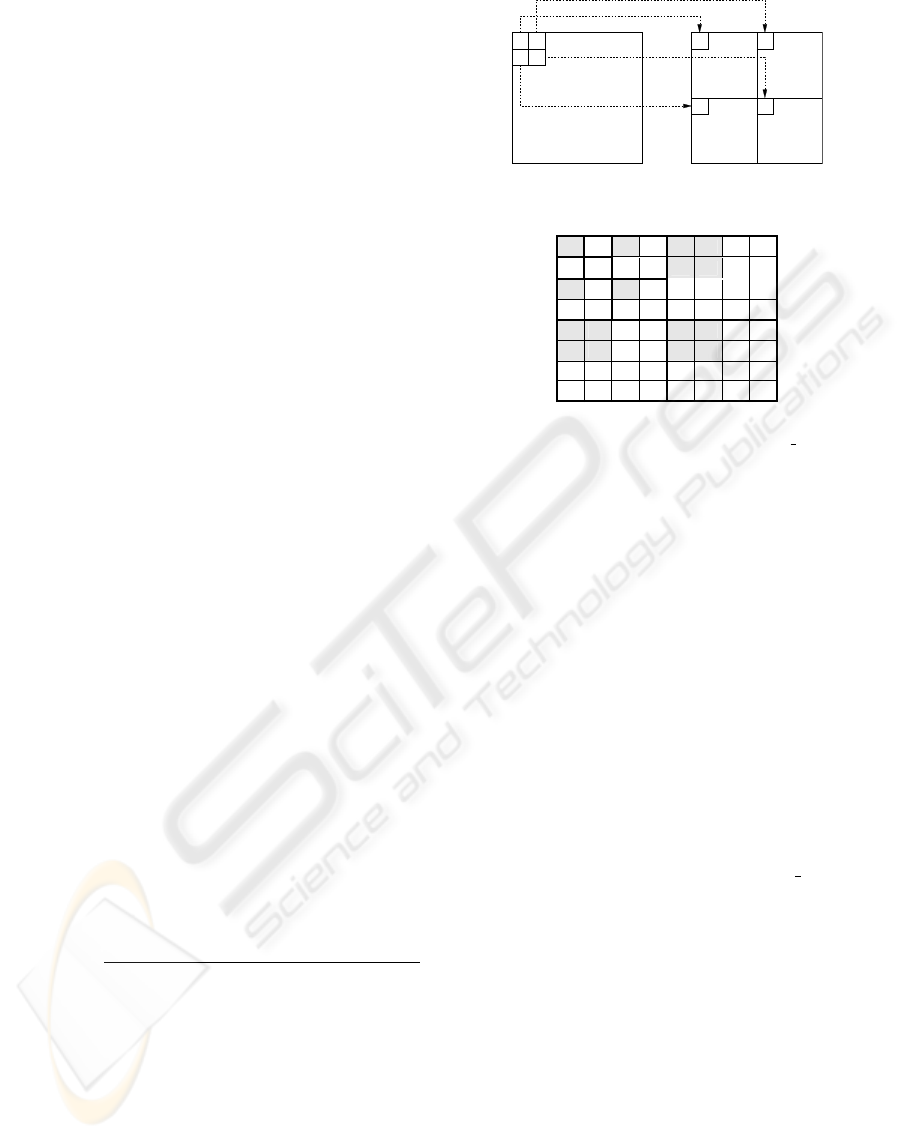
As illustrated in Figure 1, image I

is an aver-

age image of image I with half resolution. The rest

three images are called detail images. We recursively

perform this process on the average image of each it-

eration until the average image has only 1 pixel or

reaches some pre-deﬁned resolution. The result will

be the Wavelet representation of the original image I.

00 10

01 11

(a+b+c+d)/4

Figure 1: Illustration of Wavelet transform.

L0 L1 L2

Figure 2: Wavelet Transform of a (8k)

∗ blk sz data set.

Blockwise hierarchical compression scheme In

the server site, we use a blockwise hierarchical com-

pression scheme similar to (Guthe et al., 2002). Di-

vide the volumes into blocks of (2k)

, then apply

generic Haar Wavelet transform on it to get 8 blocks

of size k

. One of them will be average block, the

other 7 are detail blocks. Group 8 adjacent average

blocks again to obtain a block of size (2k)

. Re-

peat this procedure until the size of the average image

reaches m. These m blocks are the low pass ﬁltered

volume of the whole volume data. The value of k has

a tradeoff between compression rate and date redun-

dancy during transmission. Since the block will be

regarded as a unit during data transmission. Large k

value will cause data redundancy since we will trans-

mit more data than we actually needed. Small k value

usually gives low compression rate. In our case, k will

be 8 and m will be 16.

Give a 2D data set of size (8k)

∗ blk sz, repeat

the procedure described previously 2 times and ob-

tain 4 average blocks marked as A

and

(Figure 2). Each of them associates with a

quadtree (Figure 3). Take A

as example, the co-

efﬁcients marked in grey color are all the component

nodes in quadtree of A

. Local coordinate in a level

v corresponds with 3 blocks: HL, LH and HH, which

are the 3 components of node(v,i,j) in the quadtree.

Four child nodes of this node (v,i,j) in level v+1 can

be simply identiﬁed by (2i,2j), (2i,2j+1), (2i+1,2j) and

(2i+1,2j+1), which forms a pointless quadtree.

3D case is almost the same with 2D, the only dif-

ference is each node will have 7 component nodes:

LLH, LHL, LHH, HLL, HLH, HHL and HHH, and

each node has 8 child nodes.

After Wavelet volume are divided into data blocks.

RLE(run-length encoding) is performed on it block by

PROGRESSIVE TRANSMISSION AND RENDERING OF FOVEATED VOLUME DATA

A00

HH00LH00HL00

1,1 0,1 0,0 1,0

0,0

Figure 3: Quadtree of data set in Figure 2.

block in order of front to back, top to bottom and left

to right. The compressed block is a list of value(v)

and length(l) pairs.

3.1.2 Derive Foveated Volume in Wavelet

Domain

Having a volume W in Wavelet domain and ROI de-

ﬁned by a viewer, we need to derive the foveated vol-

ume W

. The ROI is deﬁned as ROI{(x, y, z),r

where (x, y, z) is the center of fovea and r indicates

its region.

The lowest resolution image of W is deﬁned as

layer 0 image, and the second lowest resolution im-

age as layer 1 image and so on. layer 0 is actu-

ally the average image of W , and layer i image can

be obtained by performing inverse Wavelet transform

to layer i-1 with the corresponding detailed coefﬁ-

cients(corresponding detailed coefﬁcients are layer i

details). The highest resolution image in W is de-

noted as layer max

layer. In general, the volume data

is of size W*H*D, and the size of the lowest resolu-

tion layer is

∗

(assuming W, H and D are

multiples of m and m is power of 2). In case the vol-

ume data V is cubic with size of N

(N is power of

2), and the Wavelet transform is processed until the

average image has size m

, m l = log

is extracted from W. It consists of all voxels

that are needed for reconstructing ROI

, where ROI

is the region of interest in the ith layer of W. The cen-

ter of ROI

is (

m l−i

), 

m l−i

, 

m l−i

) and the

size of ROI

is r

For convenience of calculation, the boundary of

ROI

can be deﬁned as

begin

.x =(x/2

(m l−i)

− s/2) (0XFFFE) (1)

begin

.y =(y/2

(m l−i)

− s/2) (0XFFFE) (2)

begin

.z =(z/2

(m l−i)

− s/2) (0XFFFE) (3)

end

.x =(x/2

(m l−i)

+ s/2) (0XFFFE) − 1 (4)

end

.y =(y/2

(m l−i)

+ s/2) (0XFFFE) − 1 (5)

end

.z =(z/2

(m l−i)

+ s/2) (0XFFFE) − 1 (6)

begin

.t, end

.t ∈ [0,minlen∗ 2

− 1],t = x, y, z

Figure 4: Extraction of the foveated data in Wavelet do-

main.

Figure 4 gives an 2D example of ROI={(9,9),6} for

a 16*16 image, where m=1, that is, the average image

size is 1

. In this example, m l = log

16 = 4. Take

layer 3 as an example, ROI

= {(4, 4), 6}, pixels in

layer 3 image with coordinate (i,j), i, j ∈ [2, 7] are in

ROI

. In order to reconstruct ROI

, layer 3 details

with coordinate (i,j), i, j ∈ [1, 3] are needed. Figure

4(b) represents the reconstructed foveated image.

3.2 Progressive Transmission

Progressive transmission is to re-order the coefﬁcients

such that more important coefﬁcients will be regarded

as high priority and being sent ﬁrst. These coefﬁcients

can be rendered in the client site separately with other

data. Less important coefﬁcients will be sent progres-

sively, step by step, to reﬁne the result image.

There are two ways of progressive transmission in

Wavelet volume rendering schemes: the region-based

and coarse-to-ﬁne.

The ﬁrst method is intuitive to implement. We just

send the Wavelet foveated volume data from inner

layer to outer layer progressively. Coefﬁcients in each

layer should be wrapped as an atomic package.

The basic idea of the second method is to send

all data blocks for constructing ROI

in each itera-

tion. At the ﬁrst iteration, boundary of ROI

m l

will

be computed and data blocks in layer m

l − 1 that

contain coefﬁcients for ROI

m l

will be added into the

data queue. All parent blocks of these blocks will also

be added into the data queue. A block is regarded as

a parent block of another block if it’s a parent node of

that block in the octree they belong to. The index of

the data block will be added into the data list when it is

added into the data queue. In iteration i, boundary of

ROI

m l−i+1

will be computed. Data blocks in layer

l − i that contain coefﬁcients for ROI

m l−i+1

and

all parent blocks of these blocks will be added into

the data queue if that block does not exist in the data

list. Repeat this procedure until coefﬁcients of ROI

are added into the data queue. If the data list doesn’t

contain all data blocks in average image after above

procedure, append the remaining average blocks into

the data queue.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

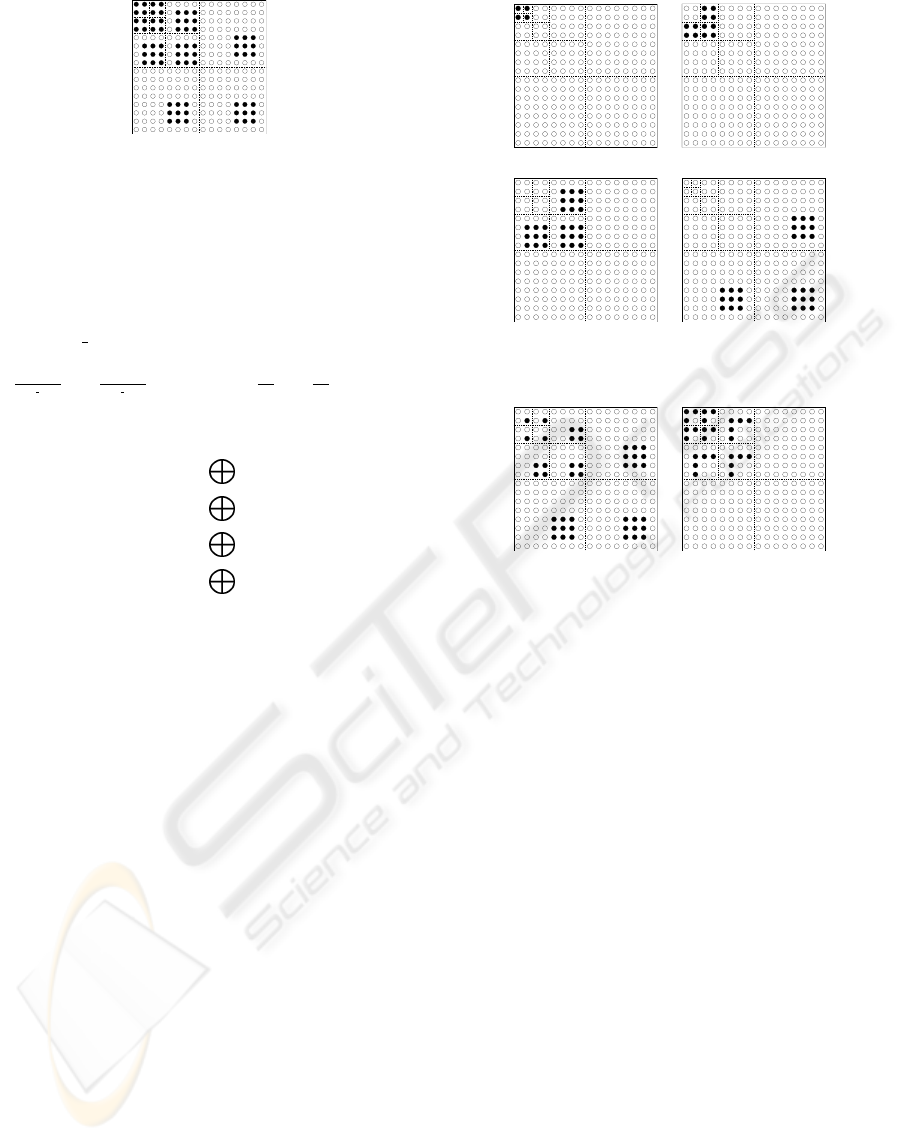
Figure 5: Wavelet foveated image.

Let’s illustrate the procedure using a 2D example.

Given a 2D image with size 128 ∗ 128, where m=16,

k=8 and ROI=(86,86),45. The average image has size

16 ∗ 16, which contains 4 data blocks, the fovea cen-

tered at coordinate (86,86) with size (45,45). In this

example, m

l = log

(128/16) = log

8=3.

Take ROI

as an example, ROI

{(

m l−i

), 

m l−i

),d} = {(

), 

), 45} =

{(43, 43), 45}.

begin

.x =(43− 45/2) (0XFFFE)=20

begin

.y =(43− 45/2) (0XFFFE)=20

end

.x = (43 + 45/2) (0XFFFE) − 1=63

end

.y = (43 + 45/2) (0XFFFE) − 1=63

begin

.x, begin

.y, end

.x, end

.y ∈ [0, 63]

Pixels in layer 2 image with coordinate (i,j),

i, j ∈ [20, 63] are in ROI

. In order to reconstruct

ROI

, layer 2 details with local coordinates (i,j),

i, j ∈ [10, 31] are needed, represented as block in-

dex (blk

,blk

), blk

,blk

∈ [1, 3]. Similarly,

ROI

= {(86, 86), 45} = [64, 107], level 3 details:

(blk

,blk

), blk

,blk

∈ [4, 6]

ROI

= {(43, 43), 45} = [20, 63], level 2 details:

(blk

,blk

), blk

,blk

∈ [1, 3]

ROI

= {(21, 21), 45} =[0, 31], level 1 details:

(blk

,blk

), blk

,blk

∈ [0, 1]

ROI

= {(10, 10), 45} =[0, 15], average blocks:

(blk

,blk

), blk

,blk

∈ [0, 1].

Figure 5 illustrates in 2D using a Wavelet foveated

image, each circle represents one data block with size

8 ∗ 8. Circles in black are data blocks that belongs to

ROI

,i ∈ [0, 3]. Figure 6 and 7 show the procedure

of the ﬁrst and second transmission methods, sepa-

rately. Black circles represents data blocks being sent

in each step. In method 2, there are only 2 steps rather

than 4. That is because we use a blockwise structure,

each block is regarded as an atomic unit. During each

iteration, we may send more data than there is actually

needed to reconstruct ROI

. Thus, detail coordinates

needed in step 3 and 4 have been sent in previous steps

as redundant data.

Step 1 Step 2

Step 3 Step 4

Figure 6: Four iterations of the region-based method.

Step 1 Step 2

Figure 7: Two iterations of the coarse-to-ﬁne method.

3.3 Progressive Volume Rendering

3.3.1 Rendering with Orthogonal Viewing

Direction

Corresponding to the two progressive transmission

methods, there are two ways of rendering: region-

based and coarse-to-ﬁne.

Algorithm 1: region-based

• Partial Volume reconstruction

Given a starting and ending coordinate (begin

begin

, begin

) and (end

, end

) of a

volume and a desired resolution scale 2

(as a

power of 2). We determine its Wavelet coefﬁcients

in each layer and reconstruct the original volume

data at a desired resolution.

Deﬁne the average image and inner most

layer to be layer 0 and outer most layer, that

is, the desired resolution layer, to be layer

l. Wavelet coefﬁcients at layer i is from

(begin

(l−i)

, begin

(l−i)

,begin

(l−i)

)

to (end

(l−i)

,end

(l−i)

,end

(l−i)

). Re-

construction starts from the average image and

the inner most detail coefﬁcients until desired

PROGRESSIVE TRANSMISSION AND RENDERING OF FOVEATED VOLUME DATA

Figure 8: Image composition.

resolution is reached.

• Progressive rendering

Given a mask with Mask

size=(s,s,s),

Mask

center=(x,y,z), num layer=L and

min

length=minlen. In the ﬁrst iteration, the

center fovea is reconstructed and rendered using

partial volume reconstruction, which is described

in previous section. In a later iteration i, 6 sub-

volumes: top, bottom, left, right, front and back are

separately reconstructed at a resolution scale 2

i−1

rendered using standard rendering algorithm and

combine the rendered result to previous rendering

image.

• Image composition

The top, bottom, left and right rendering images

obtained in each iteration are simply added to the

previous rendering image at their right position,

while front and back image needs image compo-

sition (Figure 8). For each rendering result, the

system obtains both density value and alpha value

of each pixel. An over operator is performed on

front, inner and back image, that is, (front) over

(inner) over (back).

over operator can be performed pixel by pixel.

Given image pixel A(d

,α

) and B(d

,α

). Re-

sulting pixel is C(d

,α

), where C =(A)over(B)

and d

= d

+(1− α

) ∗ d

Algorithm 2: coarse-to-ﬁne

Deﬁnition of ROI

to ROI

m l

are exactly as

described in algorithm 1. We start the rendering

procedure from ROI

, which is the average block to

the inner most layer ROI

m l

. Each layer, exclude the

inner most layer ROI

m l

, can be divided into seven

parts, denoted as, Top, Bottom, Left, Right, Front,

Back and Center. The Center part is actually the

average information for the inner layer and will be

kept for the next iteration. The process is as follows:

Take layer iROI

as an example, which is con-

structed by the Center part of ROI

i−1

and level i

detail coefﬁcients. It is divided into seven parts and

Image

Viewing Rays

Plane

Image

Slices

Volume

Figure 9: Volume being transformed to sheared object

space.

rendered. In ROI

, the number of voxels each voxel

represent is 2

m l−i

, so the intensity for each voxel in

ROI

is I =



m l−i

i=1

qα(1 − α)

i−1

Seven parts will be rendered separately and inte-

grated. The center part C

and the rendering results

of Front and Back RF

and RB

parts will be taken

down for the next iteration. C

is the average pass

for iteration i +1, and the rendering result of itera-

tion i +1, R

i+1

, will be combined with RF

and RB

using the following equation to reﬁne the rendering

result of iteration i. R =(RF

+(1− alphaRF

) ∗

i+1

)+(1− alphaRF i ∗ alphaR

i+1

) ∗ RB

Repeat

this procedure until the inner most layer is reached.

3.3.2 Rendering When Viewing From a

Non-Orthogonal Viewing Direction

When viewing from a non-orthogonal direction, the

volume transformation can be simpliﬁed by trans-

form each slice to an intermediate coordinate system,

sheared object space, for which there is a very simple

mapping from the object coordinate system and al-

lows efﬁcient projection. Then warp the intermediate

image to the image plane to produce the ﬁnal result.

Given a viewing direction θ, adjacent voxel slice

distance b and adjacent pixel distance d, the rotation

can be approximated by shifting each slice to the right

by a distance of l = b ∗ tan θ. To ensure the pixel

distance in the resulting image is still d after shear-

ing, the ray distance in the sheared object coordinate

should be m = d/ cos θ (Figure 9). After shearing,

re-sampling by interpolation should be performed to

get the voxel density value along the viewing ray.

In our schemes, we use Wavelet shear-warp fac-

torization. The difference with the above shear-warp

algorithm is we perform it in the Wavelet domain

instead of spatial domain. Factorization of the low

sub-band LLL

coefﬁcients in fovea area in each

level will approximate that of the whole volume. As

mentioned above, coefﬁcients in fovea area of all

levels is approximately 2000 times smaller than the

original volume data size, thus Wavelet shear-warp

avoids tedious shearing of the whole data set and

tremendously reduces the computational complexity.

After shearing of Wavelet coefﬁcients, they will be

input to the algorithm mentioned in orthogonal ren-

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

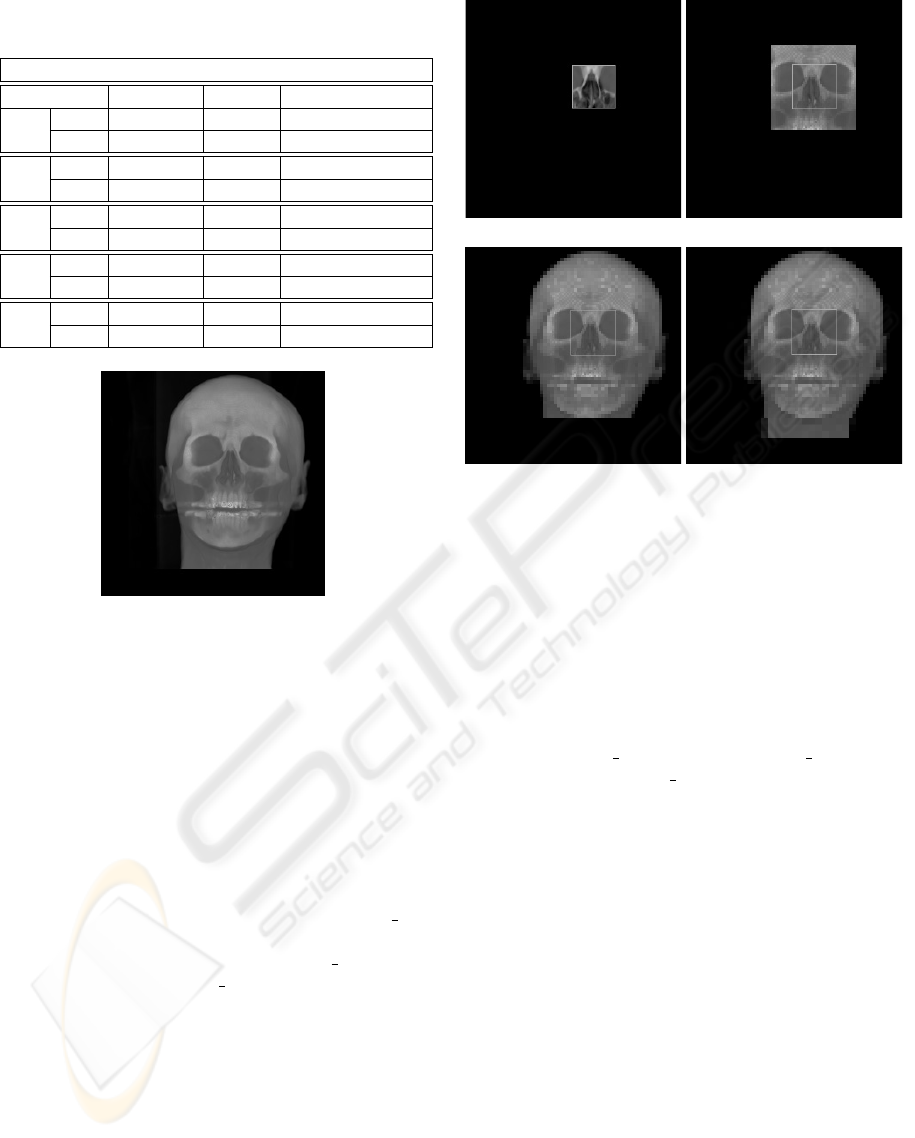
Table 3: Experiment results of the two progressive render-

ing schemes.

Experiment Results

Data(int) Image Trans/Render(s)

Itr Sche1 529,054 Fig 11(a) 0.381/0.0472

I Sche2 56,564 Fig 12(a) 0.1468/0.047

Itr Sche1 384,860 Fig 11(b) 0.125/0.0154

II Sche2 353,946 Fig 12(b) 0.1154/0.0222

Itr Sche1 296,938 Fig 11(c) 0.0938/0.0156

III Sche2 440,340 Fig 12(c) 0.1404/0.0156

Itr Sche1 0 Fig 11(d) 0.0/0.0

IV Sche2 360,002 Fig 12(d) 0.1092/0.0158

Sum Sche1 1,210,852 – 0.5998/0.0782

Sche2 1,210,852 – 0.5118/0.1006

Figure 10: Direct rendering result.

dering and produce an intermediate image by normal

projection. Warp function will then be executed on

the intermediate image to produce the ﬁnal image.

4 EXPERIMENTAL STUDY

In our experiment, we use cross-section of human

head as our example. The size of the volume data

is 256

, size of the average image is 16

, thus m l =

log

(256/16) = 4. Wavelet volume W is divided

into blocks of size 8

.Givenmask center =

{128, 128, 128} and mask

size = {50, 50, 50},we

will compare in each iteration, the result image, data

amount being transmitted and time of two schemes.

The experiment showed that, in the ﬁrst region-

based algorithm. The client can see his most inter-

ested region-of-interest(ROI) at the ﬁrst iteration. and

the client will have to wait more than two times of

the time (0.5118 second comparing to 0.381 second)

for the inner most ROI to arrive in second algorithm:

coarse-to-ﬁne, which is not desirable. Furthermore,

region-based rendering algorithm can give a clearer

rendering result of ROI. In coarse-to-ﬁne algorithm,

low resolution details arrive ﬁrst and high resolution

(a) (b)

Figure 11: Four iterations of the region-based scheme.

inner layer arrives later. Thus its clarity will be in-

terfered by low resolution coefﬁcients. However, the

client waits less time for the ﬁrst rendering result to

be displayed on the client site in coarse-to-ﬁne al-

gorithm, 0.1468 second comparing to 0.381 second.

ROI is highlighted with a square in each ﬁgure.

Another example we take here is cross-section of

human dummy with size 256

. Size of the average

image is 16

, m l =4.Givenmask center =

128, 128, 128 and mask

size =50, 50, 50. (Figure

13 and Figure 14)

5 CONCLUSION

Our work in this paper aimed at accessing to large

scale volume data stored on server repository and pro-

gressively rendered on client site in multiresolution.

In our solution, there are two ways of progressive

transmission/rendering: region-based and coarse-to-

ﬁne schemes. They are based on Wavelet foveation.

The experimental study conﬁrmed the effectiveness of

the solution.

REFERENCES

Bhaniramka, P. and Demange, Y. (2002). Opengl volu-

mizer: a toolkit for high quality volume rendering of

large data sets. In Proc. of IEEE VolVis, pages 45–54.

PROGRESSIVE TRANSMISSION AND RENDERING OF FOVEATED VOLUME DATA

Chang, E. C., Mallat, S., and Yap, C. (2000). Wavelet

foveation. Applied and Computational Harmonic

Analysis, 3(4):312–336.

Engel, K., Kraus, M., and Ertl, T. (2001). High-quality

pre-integrated volume rendering using hardware-

accelerated pixel shading. In Proc. of Eurographics /

SIGGRAPH Workshop on Graphics Hardware, pages

9–16.

Gross, M. H., Lippert, L., Dittrich, R., and Haring, S.

(1997). Two methods for wavelet-based volume ren-

dering. Computer & Graphics, 21(2):237–252.

Guthe, S., Wand, M., Gonser, J., and Strasser, W. (2002). In-

teractive rendering of large volume data sets. In Proc.

of IEEE Visualization, pages 53–60.

Hancock, D. J. and Hubbold, R. J. (1997). Efﬁcient image

synthesis on distributed architectures. In R. Earnshaw

and J. Vince, editors, The Internet in 3D, Information,

Images and Interaction, Academic Press, pages 347–

364.

Ihm, I. and Park, S. (1998). Wavelet-based 3d compres-

sion scheme for very large volume data. In Proc. of

Graphics Interface, pages 107–116.

Kim, T. and Shin, Y. (1999). An efﬁcient wavelet-based

compression method for volume rendering. In Proc.

of Paciﬁc Graphics, pages 147–156.

Lacroute, P. and Levoy, M. (1994). Fast volume rendering

using a shear-warp factorization of the viewing trans-

formation. In Proc. of SIGGRAPH, pages 451–458.

Meissner, M., Huang, J., Bartz, D., Mueller, K., and Craw-

ﬁs, R. (2000). A practical evaluation of popular vol-

ume rendering algorithms. In Proc. of IEEE VolVis,

pages 81–88.

Norton, A. and Rockwood, A. P. (March 2003). Enabling

view-dependent progressive volume visualization on

the grid. IEEE Computer Graphics and Applications,

23(2):22–31.

Pinnamaneni, P. (2003). Wavelet-Based Volume Rendering.

PhD thesis, Mississippi State University.

Pinnamaneni, P., Saladi, S., and Meyer, J. (2002). Remote

transformation and local 3d reconstruction and visual-

ization of biomedical data sets in java3d. In Proc. of

SPIE Visualization and Data Analysis 2002, volume 2,

pages 44–54.

Westenberg, M. A. and Roerdink, J. B. (2000). X-ray vol-

ume rendering by hierarchical wavelet splatting. In

Proc. of ICPR, volume 3, page 3163.

Westover, L. (1990). Footprint evaluation for volume ren-

dering. In Proc. of the 17th annual conference on

Computer graphics and interactive techniques, pages

367–376.

(a) (b)

Figure 12: Four iterations of the coarse-to-ﬁne scheme.

(a) (b)

Figure 13: Four iterations of the region-based scheme.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

(a) (b)

Figure 14: Four iterations of the coarse-to-ﬁne scheme.

PROGRESSIVE TRANSMISSION AND RENDERING OF FOVEATED VOLUME DATA