ELLIPSE DETECTION IN DIGITAL IMAGE DATA USING
GEOMETRIC FEATURES
Lars Libuda, Ingo Grothues and Karl-Friedrich Kraiss
Chair of Technical Computer Science
Aachen University, Germany
Keywords:
Ellipse Detection, Shape Analysis & Representation, Image Analysis.
Abstract:
Ellipse detection is an important task in vision based systems because many real world objects can be described
by this primitive. This paper presents a fast data driven four stage filtering process which uses geometric
features in each stage to synthesize ellipses from binary image data with the help of lines, arcs, and extended
arcs. It can cope with partially occluded and overlapping ellipses, works fast and accurate and keeps memory
consumption to a minimum.
1 INTRODUCTION
The detection of ellipses in digital image data is an
important task in vision based systems as shapes of
real world objects can often be described by geomet-
ric primitives like ellipses or be assembled by them
(Sanz et al., 1988; Radford and Houghton, 1989).Ap-
plications include but are not limited to gaze track-
ing (Canzler and Kraiss, 2004), ball tracking in soccer
games (d’Orazio et al., 2004), vehicle detection (Rad-
ford and Houghton, 1989), cell counting in breast can-
cer cell samples (Mclaughlin, 1998) or traffic sign de-
tection (Piccioli et al., 1994).
Algorithms for ellipse detection have to cope with
noisy image data and partially occluded ellipses and
they also have to produce accurate results as fast as
possible to be suitable for realtime applications. Fur-
thermore, memory usage should be low, since ellipse
detection is mostly just a preprocessing step for algo-
rithms applied in later stages.
Ellipses are described by 5 parameters: center point
(x
E
,y
E
), two semi-axes (a, b), and orientation α. The
best known method to estimate these parameters is
the standard Hough transform (Duda and Hart, 1972)
and its derivatives, e. g. (Xu et al., 1990). Special
versions of Hough transforms adapted to ellipse ex-
traction also exists (Ho and Chen, 1996; Guil and
Zapata, 1997). There is however a common disad-
vantage: Hough transforms demand a trade off be-
tween processing speed and accuracy and consume a
lot of memory. This led to the development of meth-
ods independent of any Hough transform. McLaugh-
lin (McLaughlin and Alder, 1998) proposed an algo-
rithm called ”UpWrite” for ellipse detection. It works
faster and more accurate than the above mentioned
methods, it fails however in case of partially occluded
ellipses. The latter problem is addressed by Kim et
al. (Kim et al., 2002). They introduced a two-stage
reconstruction algorithm which is able to detect par-
tially occluded ellipses but do not treat memory con-
sumption.
The algorithm presented in this paper can be added
to the category of Hough transform independent algo-
rithms. Ellipse detection is regarded as a data driven
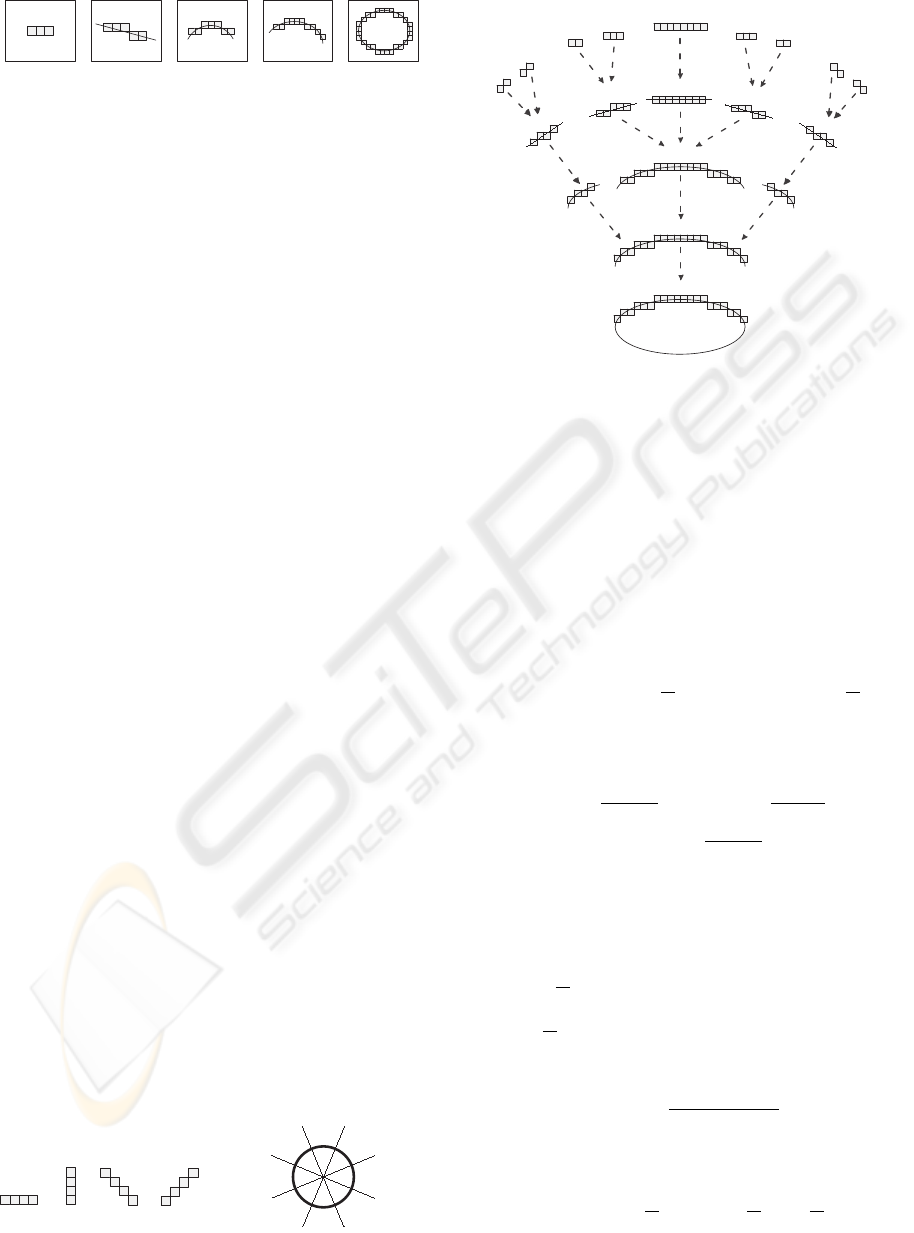
four stage filtering process (Fig. 1). The first stage
extracts short straight lines from a binary input im-
age which is created with Canny’s algorithm (Canny,
1986). In the second stage, these lines are combined
to small arcs which are synthesized to extended arcs
in the third stage. Extended arcs are finally used to
create ellipses. Each stage uses geometric features of
the extracted objects to synthesize them from objects
extracted in the previous stage.
The remaining part of this paper is structured as fol-
Line
extraction
Arc
extraction
Ext. arc
extraction
Ellipse
extraction
4 groups
of lines
8 groups
of arcs
1 group of
ext. arcs
Ellipses
Binary
image
Figure 1: Ellipse detection as four stage filtering process.
175
Libuda L., Grothues I. and Kraiss K. (2006).
ELLIPSE DETECTION IN DIGITAL IMAGE DATA USING GEOMETRIC FEATURES.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 175-180
DOI: 10.5220/0001362301750180
Copyright
c
 SciTePress

(a) Segment (b) Line (c) Arc (d) Ext. arc (e) Ellipse
Figure 2: Extracted objects during ellipse detection.
lows: Section 2 gives an overview on the entire filter-
ing process and basic definitions. Section 3 describes
the process according to Fig.1 in detail. First results
and performance of the algorithm are presented in
section 4.
2 OVERVIEW AND DEFINITIONS
The elements extracted in each processing stage are
depicted in Fig. 2. A segment consists of at least
two adjacent pixels and belongs to one of the line ori-
entation groups denoted in Fig. 3. Within each sep-
arate group of segments lines are synthesized from
adjacent segments which do not exceed a predefined
quantization error with regard to the ideal analogue
line represented by these segments. An arc is created
from at least two adjacent lines of one line orienta-
tion group. The lines must not exceed a given error in
the tangents to an estimated circle which these lines
represent. During arc extraction each line orientation
group is split in two arc orientation groups (Fig. 4)
depending on the arc’s orientation with respect to the
ellipse’s midpoint. Extended arcs consist of three ad-
jacent arcs from consecutive arc orientation groups.
Finally an ellipse is constructed from one ore more
extended arcs which describe the same ellipse with a
predefined tolerance and cover the circumference of
the described ellipse to a predefined degree.
During the filtering process it is necessary to access
the base objects of a constructed element. Therefore,
each synthesized object keeps a reference to all base
objects it is composed of. Fig. 5 visualizes this con-
cept which makes it possible to trace back each ex-
tracted object down to the single pixels belonging to
this object.
3 ELLIPSE DETECTION
This section describes the used algorithms and the
geometric features of the extracted objects in the sin-
I II III IV
Figure 3: Line groups.
I
1
=
1
III
2
=
1
II
3
=
1
IV
4
=
1
I
5
=
2
III
6
=
2
II
7
=
2
IV
8
=
2
Figure 4: Arc groups.
Segm.3
Segm.4
Segment 5
Segm.6
Segm.7
Line 2
Line 3
Line 4
Arc 1
Arc 2
Arc 3
Extended Arc
Ellipse
Line 1
Line 5
Segm.1
Segm.2
Segm.8
Segm.9
Figure 5: Extracted elements and their relationships.
gle filter stages. All algorithms are described for ori-
entation group I only. The same algorithms may be
applied to all other groups after rotating the pixel co-
ordinates by ±45
◦
and 90
◦
respectively.
3.1 Line Extraction
In the first step lines are extracted from the bi-
nary input image using the algorithm proposed by
Kim (Kim et al., 2003). The algorithm outputs for
each line orientation group g[I,II,III,IV ] a set
of n
g
lines LS
g
= {L
i
,i =1..n
g
} with L
i
=
(x
si
,y
si
,x
ei
,y
ei
,x
Mi
,y
Mi
, Θ
i
) describing the start
position (x
si
,y
si
), end position (x
ei
,y
ei
), midpoint
(x
Mi
,y
Mi
), and slope Θ
i
of each line. The last three
elements are calculated by the following equations:
x
Mi
=
x
si
+x
ei
2
,y
Mi
=
y
si
+y
ei
2
Θ
i
= tan
−1

y
si
−y
ei
x
ei
−x
si

3.2 Arc Extraction
The second processing stage combines lines to small
arcs for each line set LS
g
. The algorithm selects a
target line L
i
from LS
g
and stores it in an empty arc
line set LA. Subsequently it searches for a candi-
date line L
j
within an adaptive triangular search win-
dow (Fig. 6a). With the predefined maximum distance
D
line
the window parameters are calculated by:
GAP
x1
=
x
ei
− x
si
+1
2
− 1
GAP
x2
= D
line
GAP
y
= D
line
− 1
If a candidate line L
j
is found L
i
and L
j
will be
considered parts of the same arc if they satisfy the
following two conditions:
VISAPP 2006 - IMAGE ANALYSIS
176

Search window
GAP
x1
GAP
x2
GAP
y
L
i
Target
Candidate
L
j
Figure 6a: Search window for arcs.
i
L
i
L
j
j
ij
Figure 6b: Intersection angle.
est
j
err
L
j
L
i
Figure 6c: Tangent error.
1. The intersection angle Θ
ij
= |Θ
i
− Θ
j
| has to be
in the range 0
◦
≤ Θ
ij
≤ 45
◦
(Fig. 6b).
2. The error of Θ
j
compared to the estimated circle
tangent Θ
est
in the midpoint (x
Mj
, y
Mj
) of L
j
must not exceed a given angle tolerance Θ
err,line
(Fig. 6c). By using all lines in LA and the can-
didate line L
j
the circle midpoint (˜x
C
, ˜y
C
) and its
radius
˜
R are estimated with the help of Thomas’ al-
gorithm (Thomas and Chan, 1989). Now, Θ
est
can
be calculated and the condition checked by:
Θ
est
= tan
−1

x
Mj
−˜x
C
˜y
C
−y
Mj

|Θ
j
− Θ
est
| < Θ
err,line
If L
j
satisfies all conditions it is added to LA and
a new iteration starts with L
j
as the new target. If L
j
is not found or fails either test and LA contains more
than one element, a new arc is found. In this case the
final circle parameters x
C
, y
C
and R are estimated
from the lines contained in LA and stored in a vector
A
=(LA,x
C
,y
C
,R). Depending on the arc’s po-
sition to the estimated circle midpoint, it is assigned
to one of two possible arc groups (see Fig. 4). After-
wards the algorithm chooses a new target line from
LS
g
which is not already part of an arc and starts at
the beginning. It terminates when all lines have been
visited.
After application of this algorithm to all line sets
the result is a set of n
g
arcs AS
g
= {A
i
,i =
1..n
g
} with A
i
=(LA
i
,x
Ci
,y
Ci
,R
i
) for each group
g[1..8].
3.3 Extended Arc Extraction
In the third step arcs are combined to extended arcs.
This is necessary because arcs are too small for an
accurate ellipse estimation. For one extended arc
three adjacent arcs A
a
, A
b
and A
c
of consecutive
arc groups have to be found. This can be achieved
by selecting a target arc A
b
of the arc set AS
g
and
searching the sets AS
g −1
and AS
g +1
for the candi-
date arcs A
a
and A
c
. To ensure that target and candi-
dates describe the same ellipse, several conditions are
checked. Conditions 1-3 apply to both arc pairs a/b
and b/c, but are described for a/b only. Conditions 4-
6 apply to all three arcs a/b/c. For arc pairs we define
the gap vector
−→
G pointing from the endpoint of one
arc to the start point of the other. We define (a
, b)
to be the angle between the vectors a
and b.
1. The absolute distance of the arcs in horizontal
and vertical direction given by |G
x
| and |G
y
| must
not exceed the predefined maximum distance D
arc
.
G
A
a
A
b
|G
x
|≤D
arc
|G
y
|≤D
arc
2. The relative distance d
rel
of the arcs must be
greater than the predefined minimum d
min
. Vector
−−→
AB connects the arc startpoints and
−→
A ,
−→
B are vec-
tors pointing from start- to endpoint of each arc.
A
B
AB
d
rel
=
|
−−→
AB|
|
−→
A |
>d
min
3. The gap angles of both arcs must be less than the
predefined maximum Θ
gap,max
. With L
a
as last line
of arc A
a
and L
b
as first line of A
b
the gap angles can
be calculated as the angles between these lines and
−→
G.
L
L
gap,a
G
gap,b
b
a
Θ
gap,a
= (L
a
,
−→
G)
Θ
gap,b
= (L
b
,
−→
G)
4. The inner angles of all arc line pairs must be less
than 90
◦
. Let LX be the set of all lines of A
a
, A
b
, A
c
and L
i
, L
j
be two lines of LX. The inner angles are
the angles between their normal vectors
−→
N
i
,
−→
N
j
and
their startpoint connection
−→
IJ and
−→
JI respectively.
L
L
IJ, JI
N
N
i
i
j
j
in,i
in,j
Θ
in,i
= (
−→
N
i
,
−→
IJ)
Θ
in,j
= (
−→
N
j
,
−→
JI)
5. The tangent error of all arc lines compared to
the estimated ellipse must be less than the predefined
maximum Θ
err,arc
. Using A
a
, A
b
, A
c
the ellipse
ELLIPSE DETECTION IN DIGITAL IMAGE DATA USING GEOMETRIC FEATURES
177

parameters ˜x
E
,˜y
E
,˜a,
˜
b,˜α are estimated with the algo-
rithm proposed in (Fitzgibbon and Fisher, 1999). For
each arc line L
i
we compare the line tangent Θ
i
and
the ellipse tangent Θ
est
in the midpoint (x
Mi
,y
Mi
).
err
est
i
L
i
Θ
est
=tan
−1
−
˜
b
2
·x
Mi
˜a
2
·y
Mi
|Θ
i
− Θ
est
| < Θ
err,arc
6. The line beam of the three extended arcs must run
within the maximum distance D
LB
from their esti-
mated ellipse center point C
i
=(˜x
Ei
, ˜y
Ei
). With L
a
being the first line of A
a
and L
c
being the last line
of A
c
the line beam LB
i
can be calculated as the line
passing through the points T
i
and M
i
, whereas T
i
is
the intersection point of the line tangents Θ
a
and Θ
c
and M
i
is the midpoint of the connection of the mid-
points of L
a
and L
c
.
LB
i
C
i
M
i
T
i
L
a
L
c
A
a
A
b
A
c
a c
If all three arcs satisfy all conditions, a new ex-
tended arc X
is created. After all arcs have been
visited the result of this stage is a set of n ex-
tended arcs XS = {X
i
,i =1..n} with X
i
=
(A
ai
, A
bi
, A
ci
, ˜x
Ei
, ˜y
Ei
, ˜a
i
,
˜
b
i
, ˜α
i
,LB
i
).
3.4 Ellipse Extraction
In the last step extended arcs are used to create el-
lipses. The algorithm merges extended arcs X
i
be-
longing to the same ellipse E
j
to a set XE
j
=
{X
i
,i =1..n} in three steps. Merged extended arcs
X
i
are removed from the set XS because they can be
part of one ellipse only.
Because each extended arc consists of three arcs,
adjacent extended arcs can overlap in up to two arcs.
In the first step, these overlapping arcs are identi-
fied by searching extended arcs composed of identical
arcs. The identified objects are then checked by three
conditions whether they describe the same ellipse:
1. The tangent error of all arc lines compared to the
jointly estimated ellipse must be less than Θ
err,arc
.
This is identical to condition 5 in section 3.3.
2. The line beams of all extended arcs have to inter-
sect within the maximum distance D
LB
from the
ellipse center point.
3. The ellipse contour mismatch of the start- and end-
points (x
i
,y
i
) of all arc lines must not exceed the
predefined maximum δ
ell,max
and is checked by:






x
i
˜a

2
+

y
i
˜
b

2
− 1





<δ
ell,max
In the second step non-overlapping extended arcs
are taken from XS and it is tried to assign them to
one of the merge sets XE
j
created in the first step.
An extended arc has to fulfill the same conditions 1-3
to become part of a set XE
j
.
The third step tries to merge the remaining ex-
tended arcs in XS. The algorithm compares the el-
lipse parameters of each extended arc and merges
those that match with a predefined accuracy. The el-
lipse center must not differ more than D
match
and
the semi-axis have to match with a relative percent-
age r
match
.
Finally the ellipse parameters x
Ej
,y
Ej
,a
j
,b
j
, and
α
j
are calculated for every merge set XE
j
. Subse-
quently, the ellipse circumference C
j
is approximated
by:
C
j
≈ π

1.5(a
j
+ b
j
) −

a
j
b
j

If the set of all arc lines in XE
j
covers C
j
to a
predefined percentage C
min
, the ellipse is added to
the final ellipse set ES = {E
j
,j =1..n} with
E
j
=(XE
j
,x
Ej
,y
Ej
,a
j
,b
j
,α
j
).
4 RESULTS
This section presents results which were obtained on
a Pentium 4 system with 2.8 GHz. Fig. 6 visualizes
all intermediate results during ellipse extraction on an
outdoor real world image of size 800 x 600 pixels. Al-
though there is lots of clutter in the binary edge im-
age all relevant ellipses are found and no false pos-
itives are detected. However, false positives may be
detected in case lines form a partial ellipse which ac-
tually do not belong to a real world ellipse as demon-
strated in the top row of Fig. 7. This happens because
lines and the derived structures are the only infor-
mation used to search for ellipses. By incorporating
more knowledge in the detection process, e.g. color
or texture analysis within an ellipse candidate, false
positives can be reduced. This is one task for future
work.
Tab. 1 summarizes the amount of extracted objects
in each filter stage, the memory consumption and
processing time for the image in Fig.6. Each process-
ing stage reduces the number of processed objects ap-
proximately by one order of magnitude, which means
that the time consuming checks are only applied to
very few objects. Memory is allocated only for the
extracted objects. Of course memory consumption
and processing time depend on the complexity of the
VISAPP 2006 - IMAGE ANALYSIS
178

Figure 6: Visualization of the different steps during ellipse detection in an outdoor real world image. From top left to bottom
right: Input image, binary edge image, lines, arcs, extended arcs and ellipses. The extracted elements are superimposed on
the input image (800 x 600 pixels).
Table 1: Memory consumption and processing time for im-
age (800x 600 pixels) in Fig. 6.
Object Quantity Memory usage Time
Segments 89295 2092.9 KByte 62 ms
Lines 9094 931.8 KByte 172 ms
Arcs 540 63.7 KByte 47 ms
Ext. arcs 21 3.6 KByte 12 ms
Ellipses 5 0.3 KByte 3 ms
Total 3092.3 KByte 296 ms
original image. On an image of size 320x 240 pix-
els the average processing time is 45 ms. However,
with a more sophisticated preprocessing which nar-
rows the search space, speed can be increased and
memory consumption can be decreased even further.
This optimization is the second task for future work.
The two bottom rows of Fig.7 show example im-
ages demonstrating the detection of overlapping and
partially occluded ellipses. All ellipses are found in
all images but their accuracy depends on the amount
of their visible circumference. The more data is avail-
able for one ellipse the more precise are its estimated
parameters.
Finally, the number of parameters introduced in
section 3 has to be discussed. On the one hand many
parameters allow to adapt the algorithm to nearly all
situations but on the other hand it is sometimes hard to
find the optimal configuration. For the latter case we
ranked the parameters to identify the important once.
Tab. 2 shows which parameters should be changed
Figure 7: Examples for the detection of false positives (top
row) and overlapping and partially occluded (bottom rows)
ellipses in real world images. All results were obtained with
the same parameter settings (see Tab. 2).
first to adapt the algorithm in case it does not produce
the desired results with its default settings. Parame-
ters marked with ”+” are most important for an adap-
ELLIPSE DETECTION IN DIGITAL IMAGE DATA USING GEOMETRIC FEATURES
179

Table 2: Importance of parameters. The 3
rd
column shows
the values used to obtain the results in Fig. 7.
Symbol Importance Value Ref.
D
line
- 3 pix. 3.2
Θ
err,line
+ 18.0
◦
3.2
D
arc
+ 37 pix. 3.3
d
min
- 0.47 3.3
Θ
gap,max
- 30.0
◦
3.3
Θ
err,arc
+ 14.0
◦
3.3, 3.4
D
LB
o 4 pix. 3.3, 3.4
δ
ell,max
- 2.7 3.4
D
match
o 5.0 3.4
r
match
- 0.8 3.4
C
min
+ 0.25 3.4
tion and have to be changed first. Parameters marked
with ”o” can be used for fine tuning the results and
parameters marked with ”-” do not influence the final
results. They can be replaced by constant values in
future versions of the algorithm. In this way only four
parameters remain which is a fair amount for an algo-
rithm of this complexity. However, all ellipses in this
paper were found using the same parameter settings.
5 CONCLUSION
This paper introduces a fast and robust algorithm for
ellipse extraction from binary image data based on
a four stage data driven filtering process. The ob-
tained results support the conclusion that it is able to
cope with partially occluded ellipses and noisy image
data. It produces accurate results and keeps memory
consumption to a minimum. Future work includes
the incorporation of more knowledge, e.g. color in-
formation, to distinct between real ellipses and false
positives and speed optimization. The algorithm is
available as open source in the LTI-L
IB project at
http://ltilib.sourceforge.net.
REFERENCES
Canny, J. (1986). A computational approach to edge de-
tection. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 8(6):679–698.
Canzler, U. and Kraiss, K.-F. (2004). Person-adaptive fa-
cial feature analysis for an advanced wheelchair user-
interface. In Drews, P., editor, Conference on Mecha-
tronics & Robotics, volume Part III, pages 871–876,
Aachen. Sascha Eysoldt Verlag.
d’Orazio, T., Guaragnella, C., Leo, M., and Distante, A.
(2004). A new algorithm for ball recognition using
circle hough transform and neural classifier. Pattern
Recognition, 37(3):393–408.
Duda, R. and Hart, P. (1972). Use of the hough transforma-
tion to detect lines and curves in pictures. Communi-
cations of the ACM, 15(1):11–15.
Fitzgibbon, A. W.and Pilu, M. and Fisher, R. B. (1999).
Direct least-squares fitting of ellipses. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
21(5):476–480.
Guil, N. and Zapata, E. (1997). Lower order circle
and ellipse hough transform. Pattern Recognition,
30(10):1729–1744.
Ho, C. and Chen, L. (1996). A high-speed algorithm for el-
liptical object detection. IEEE Transactions on Image
Processing, 5(3):547–550.
Kim, E., Haseyama, M., and Kitajima, H. (2002). Fast
and robust ellipse extraction from complicated im-
ages. In Proceedings of the first International Con-
ference on Information Technology & Applications,
Bathurst, Australia.
Kim, E., Haseyama, M., and Kitajima, H. (2003). Fast line
extraction from digital images using line segments.
Systems and Computers in Japan, 34(10):76–89.
Mclaughlin, R. (1998). Randomized hough transform: Im-
proved ellipse detection with comparison. Pattern
Recognition Letters, 19(3-4):299–305.
McLaughlin, R. and Alder, M. (1998). The Hough trans-
form versus the UpWrite. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 20(4):396–
400.
Piccioli, G., Michelli, E., Parodi, P., and Campani, M.
(1994). Robust road sign detection and recognition
from image sequences. In Proceedings of the IEEE
Symposium on Intelligent Vehicles, pages 278–283,
Paris, FR.
Radford, C. and Houghton, D. (1989). Vehicle detection in
open-world scenes using a hough transform technique.
In Third International Conference on Image Process-
ing and its Applications, pages 78–82, Warwick, UK.
Sanz, J., Hinkle, E., and Jain, A. (1988). Radon and Pro-
jection Transform-Based Computer Vision. Springer
Verlag.
Thomas, S. and Chan, Y. (1989). A simple approach for
the estimation of circular arc center and its radius.
Computer Vision, Graphics, and Image Processing,
45(3):362–370.
Xu, L., Oja, E., and Kultanen, P. (1990). A new curve de-
tection method: Randomized hough transform (rht).
Pattern Recognition Letters, 11(5):331–338.
VISAPP 2006 - IMAGE ANALYSIS
180