A NOVEL APPROACH TO PLANAR CAMERA CALIBRATION

Ashutosh Morde, Mourad Bouzit, Lawrence Rabiner

CAIP, Rutgers University

96 Frelinghuysen Road, Piscataway, NJ 08855

Keywords:

Camera Calibration, Image of Absolute Conic, Vanishing Line, Concentric Circles.

Abstract:

Camera calibration is an important step in 3D reconstruction of scenes. Many natural and man made objects

are circular and form good candidates as calibration objects. We present a linear calibration algorithm to

estimate the intrinsic camera parameters using at least three images of concentric circles of unknown radii.

Novel methods to determine the projected center of concentric circles of unknown radii using the projective

invariant, cross ratio, and calculating the vanishing line of the circle are proposed.

The circular calibration pattern can be easily and accurately created. The calibration algorithm does not require

any measurements of the scene or the homography between the images. Once the camera is fully calibrated

the focal length of zooming cameras can be estimated from a single image. The algorithm was tested with real

and synthetic images with different noise levels.

1 INTRODUCTION

Camera calibration is an essential step in many com-

puter vision and photogrammetric applications. It

consists of recovering the metric properties which are

encoded as a set of so-called internal parameters. It

has been a subject of active research with numer-

ous methods (Tsai, 1987; Strum and Maybank, 1999;

Zhang, 2000). Once the cameras are calibrated, the

projective relationship from 3D space to 2D image

can be established.

The existing camera calibration techniques can be

broadly classiﬁed as linear, (Grosky and Tamburino,

1990; Strum and Maybank, 1999), and non-linear

(Heikkila, 2000; Meng and Hu, 2003). The non linear

techniques have the disadvantage of requiring good

initial estimates of the intrinsic parameters and being

computationally intensive. If the starting point of the

algorithm is not well chosen the solution can diverge

or can get trapped in a local minimum. A linear ap-

proach is not plagued with these problems.

Camera calibration can also be broadly classiﬁed

based on the type of calibration object, viz. 3D cali-

bration object, and 2D calibration object. Most com-

monly used calibration procedures described in the

computer vision literature rely on a calibration object

with control points whose 3D coordinates are known

with a high degree of accuracy to obtain accurate re-

sults (Tsai, 1987; Heikkila, 2000). As compared to

a 3D calibration object, 2D calibration patterns offer

the advantage of easily creating an accurate calibra-

tion object; the calibration pattern can be printed on

a laser printer and mounted on a ﬂat surface. Tech-

niques utilizing planar patterns require multiple views

of the calibration object (Strum and Maybank, 1999;

Zhang, 2000). The camera motion between the im-

ages need not be known.

Conics can be used instead of control points as it

is easy to match correspondences. They project onto

the image plane as ellipses from any view and have

been widely used before to estimate the camera pose

(Kanatani and Liu, 1993; Chen and Huang, 1999).

The use of circles and ellipses as 2D calibration ob-

jects have been increasing. There are various non-

linear planar calibration algorithms which use circles

and ellipses of known dimension as calibration object

(Yang et al., 2000; Kim and Kweon, 2001; Kim et al.,

2002; Abad et al., 2004).

We propose a novel linear method, which exploits

the Thales theorem for circles, to calculate the van-

ishing line of the circle and the corresponding Image

of the Circular Points (ICP’s). The camera intrinsic

parameters are then determined, from at least 3 im-

ages, using the Image of Absolute Conic (IAC) as

Morde A., Bouzit M. and Rabiner L. (2006).

A NOVEL APPROACH TO PLANAR CAMERA CALIBRATION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 87-92

DOI: 10.5220/0001362500870092

 SciTePress

the calibration object. The projected center of con-

centric circles required by the calibration algorithm

is accurately determined using the cross ratio with-

out any knowledge of the circle radii. The calibration

method has the advantage of not requiring any metric

measurements nor any correspondences between the

images.

The paper is organized as follows. In section 2 we

describe the theory used; in section 3 we present novel

algorithms to ﬁnd the projected center of concentric

circles and the vanishing line of the circle. In section

4 we discuss the camera calibration algorithm and the

results, which is followed by the conclusion.

2 THEORY

We adopt a perspective camera model with intrinsic

matrix K,

K =



0 f

001



. (1)

where f

and f

are the effective camera focal lengths

along the camera axes u and v, s is the skew of the

CCD plane and (u

) is the coordinate of the image

center. A homogeneous point

X =[X, Y, Z, 1] gets

projected to ˜x =[u, v, w] as

λ˜x = K [RT]

i.e. λ˜x = KM

ext

X = M

. (2)

where M

ext

is the camera extrinsic parameter matrix

with R and T , the rotation matrix and the translation

vector from the world to the camera system respec-

tively and λ is a non zero scale factor.

Let a circle with radius R

and center at [X

, 0]

lie in the z plane of the world coordinate system. A

homogeneous point [X, Y, 1] on the circle satisﬁes the

equation

[XY 1]

⎡

⎣

10 −X

01 −Y

−X

−Y

+ Y

− R

⎤

⎦





i.e. X

CX =0

. (3)

This circle gets projected as the ellipse X

AX =

0, where A is the matrix deﬁning the ellipse and is

related to the circle up to a scale factor λ by

λA = H

−T

−1

. (4)

where H = K [

]=KM

is the ho-

mography transforming the circle into an ellipse; R

and R

are the ﬁrst and second columns of the rota-

tion matrix R.

All circles pass through the circular points I =

(1,i,0)

and J =(1, −i, 0)

whose position is in-

variant to plane similarity transformation. A special

circle is the absolute conic which is an imaginary cir-

cle located in the plane at inﬁnity and is also invariant

to similarity transformations. All circles intersect the

absolute conic and the line at inﬁnity at the circular

points (Hartley and Zisserman, 2000). The absolute

conic, C

∞

= I, forms a natural calibration object

with the IAC, ω, being related to the intrinsic matrix

under the homography H

∞

= KM

∞

ω = H

−T

∞

−1

∞

=(KM

∞

)

−T

I (KM

∞

)

−1

= K

−T

∞

−1

∞

−1

= K

−T

−1

(5)

(a)

(b)

Figure 1: Projection of concentric circles.

3 FROM CIRCLES TO

RECTANGLES

3.1 Projected Center of Circle

A 3D circle gets projected as an ellipse from any view

but the projected center of the 3D circle does not co-

incide with the center of the ellipse (J.L.Mundy and

A.Zisserman, 1992). The projected center of concen-

tric circles lies on the line joining the centers of the

projected ellipses (Kim and Kweon, 2001) and it can

be determined by using the projective invariant, cross

ratio. The cross ratio of four points (P

)

is deﬁned as

VISAPP 2006 - IMAGE FORMATION AND PROCESSING

(a)

(b)

Figure 2: Projected center of circle.

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0 0.5 1 1.5 2 2.5 3 3.5 4

Mean Error

Noise in pixels

(a) Projected circle center error

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0 0.5 1 1.5 2 2.5 3 3.5 4

Std. Dev.

Noise in pixels

(b) Std. Dev. of projected circle

center

Figure 3: Inﬂuence of noise on ﬁnding projected center of

circle.

(a) Rectangle inscribed by two

diameters

(b) Its projection

Figure 4: Rectangle inscribed in a circle.

CR(P

d(P

)∗d(P

)

d(P

)∗d(P

)

. (6)

where d (j, k)=



− x

)

+(y

− y

)

is the

distance between points j and k. With three ﬁxed

points the cross ratio is a monotonic function of the

fourth point. As any one point is made to move

along the line joining all the points the cross ratio in-

creases/decreases. For example, in ﬁgure 1, moving

point P

closer to point P

causes the cross ratio to

decrease while moving point P

away from point P

causes the cross ratio to increase.

Consider four points lying on the diameter of two

concentric circles with center P

as shown in ﬁgure

1(a). For these four points we have

CR(P

)=CR(P

) . (7)

As the cross ratio is a projective invariant the same

is true for ﬁgure 1(b) which is a projection of the con-

centric circles in ﬁgure 1(a). The algorithm for ﬁnd-

ing the circle center then involves :

1. Initializing the projected circle center as the inner

ellipse center

2. A binary search along the line joining the two el-

lipse centers bounded by points P

and P

A NOVEL APPROACH TO PLANAR CAMERA CALIBRATION

0 0.5 1 1.5 2 2.5 3 3.5 4

Mean Error

Noise in pixels

(a) Mean error for f

and f

0 0.5 1 1.5 2 2.5 3 3.5 4

Mean Error

Noise in pixels

(b) Mean error for u

and v

0 0.5 1 1.5 2 2.5 3 3.5 4

Mean Error

Noise in pixels

0 0.5 1 1.5 2 2.5 3 3.5 4

Std. Dev.

Noise in pixels

(d) Std. Dev. of f

and f

0 0.5 1 1.5 2 2.5 3 3.5 4

Std. Dev.

Noise in pixels

(e) Std. Dev. of u

and v

0 0.5 1 1.5 2 2.5 3 3.5 4

Std. Dev.

Noise in pixels

(f) Std. Dev of skew

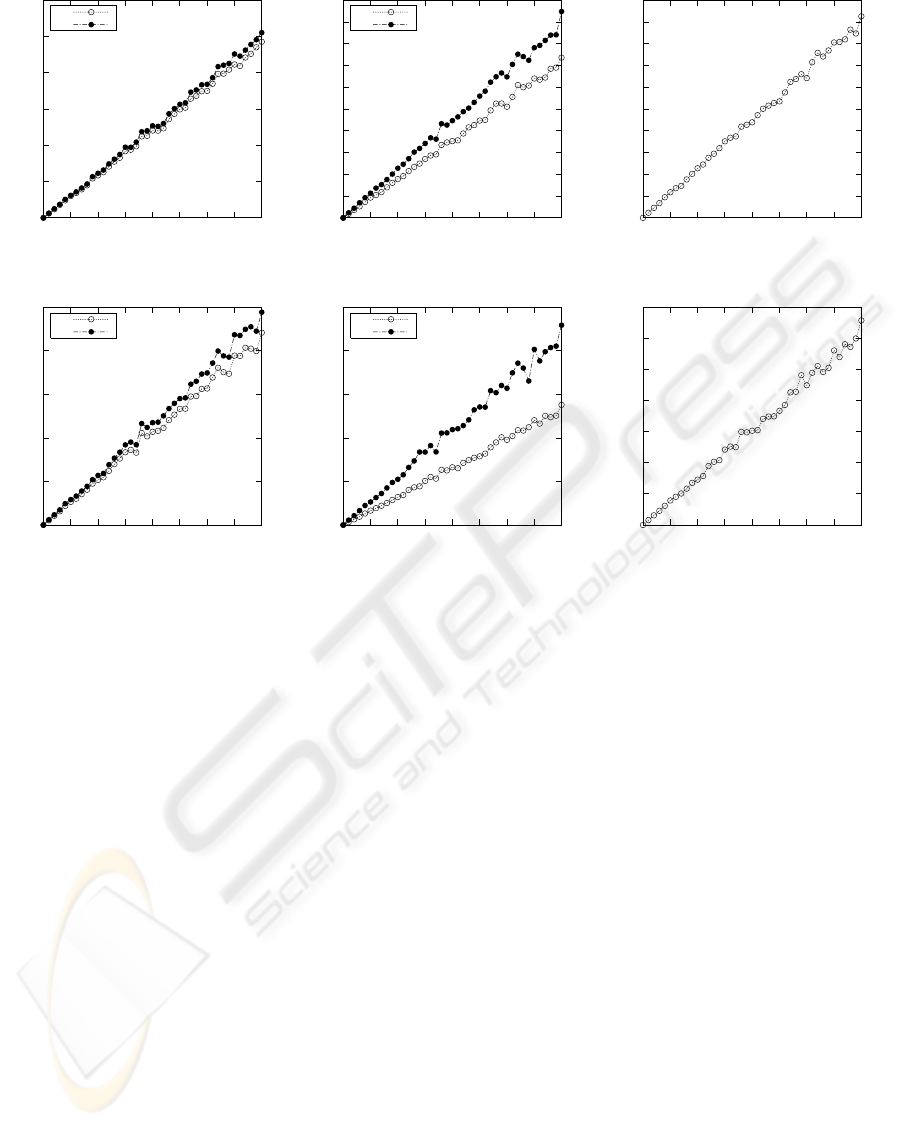
Figure 5: Inﬂuence of noise in calculating intrinsic parameters.

(a) If CR(P

) >CR(P

)

then move P

towards point P

(b) If CR(P

) <CR(P

)

then move P

towards point P

Due to the monotonic nature of the cross ratio the

algorithm always converges, usually in 2-3 iterations.

In ﬁgure 2 the circle center was correctly calculated as

(333.86, 190.76) for a real image. Figure 3 shows the

result of a simulation of ﬁnding the projected center

of circle; the simulation parameter details are given

in section 4.2 along with the calibration results . The

algorithm is observed to be very robust to noise per-

turbations and correctly calculates the projected circle

center while the ellipse centers do not coincide with

the projected circle center.

3.2 Vanishing Line of a Circle

The vanishing line is the image of the line at inﬁnity

and its intersection with the image of a circle gives

the image of circular points. Any two lines through a

circle center form the diagonals of a rectangle. Figure

4 illustrates this with lines P

and P

be-

ing the diameters of the circle and inscribing a rectan-

gle P

. The procedure for ﬁnding the vanish-

ing line starts off with intersecting two lines passing

through the projected center of circle with an ellipse,

the image of the circle. This gives a quadrilateral

, ﬁgure 4(b), which is the image of a rec-

tangle. Thus intersecting lines P

and P

gives

one vanishing point while intersecting lines P

and

gives another vanishing point. The two van-

ishing points are then used to compute the vanishing

line.

4 CAMERA CALIBRATION

4.1 Calibration Algorithm

The procedure for calibrating the camera involves the

following steps :

• Capture 3 views of the concentric circles and for

each image

– ﬁt ellipses using the direct least squares method

(Fitzgibbon et al., 1999)

VISAPP 2006 - IMAGE FORMATION AND PROCESSING

2.5

3.5

4.5

5.5

3 3.5 4 4.5 5 5.5 6

Std. Dev.

Number of images

(a) Std. Dev. of f

and f

1.5

2.5

3.5

4.5

5.5

3 3.5 4 4.5 5 5.5 6

Std. Dev.

Number of images

(b) Std. Dev. of u

and v

0.5

1.5

2.5

3 3.5 4 4.5 5 5.5 6

Std. Dev.

Number of images

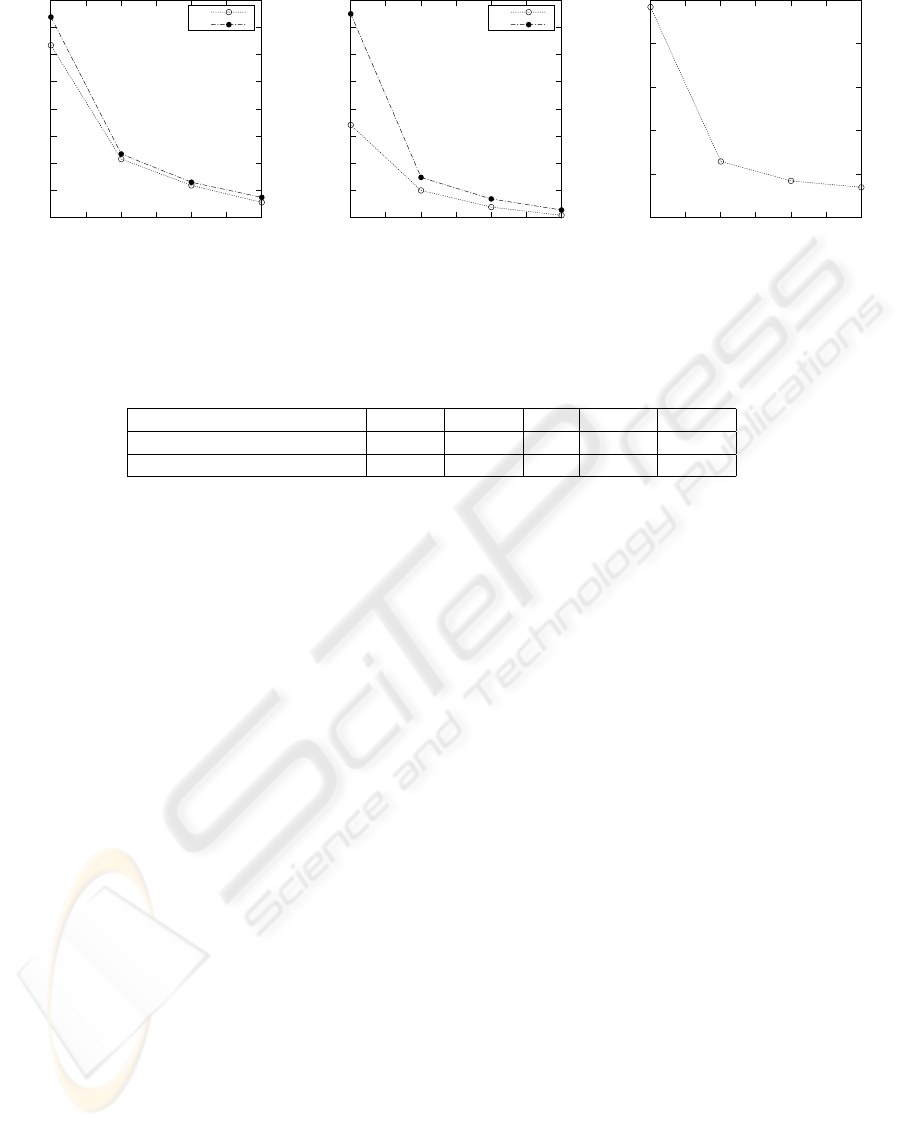
Figure 6: Effect of increasing the number of images on calculating intrinsic parameters.

Table 1: Comparison of Calibration results.

s u

Proposed Algorithm 812.03 810.31 -0.6 314.25 239.47

Zhang’s Planar Calibration 788.83 789.27 0 318.73 241.13

– Calculate the projected center of the circles as

described in section 3.1

– Estimate the vanishing line as explained in sec-

tion 3.2

– Intersect the vanishing line with an ellipse to get

the two ICP’s.

• Fit an ellipse to the 6 ICPs to obtain the Image of

IAC

• Perform Cholesky Decomposition of the IAC ma-

trix to obtain the camera intrinsic parameters

Once the camera is calibrated the ICP’s from a sin-

gle image can be used to estimate the focal length of

zooming cameras (Strum and Maybank, 1999).

4.2 Calibration Result

The accuracy of the proposed algorithm was tested

using simulations. The simulations were performed

with circles of radii 120mm and 60mm with 400

points per circle and a camera with intrinsic matrix

K =



845.79 0.1 315.24

0 875.46 226.13

001



. (8)

The camera was setup in 6 different locations with

the projection of the larger circle varying as an ellipse

with half major axis length of 130-190 pixels and the

half minor axis length of 80-150 pixels. For trials with

less than 6 images, all possible camera pose combina-

tions were used. Thus when calibrating using just 3

images, the 6 camera poses provide





= 120 sets to

work with. The projected circle points were perturbed

with zero mean gaussian noise while the standard de-

viation was varied from 0 to 4 pixels. Figure 5 shows

the accuracy of the technique in estimating the intrin-

sic parameters at various noise levels for 200 indepen-

dent trials. The estimation error is found to be small

and its standard deviation increases with the noise lev-

els. In ﬁgure 6 we observe that the standard deviation

of the estimated intrinsic parameters decreases with

the increase in the number of images used for calibra-

tion.

The algorithm was also tested with real images

of dimension 640 by 480 taken by a Sony Lipstick

camera. Table 1 gives the results of camera calibra-

tion with the proposed algorithm and Zhang’s (Zhang,

2000) method. The results are comparable, the dif-

ference could be accounted by the use of non linear

minimization and estimation of distortion coefﬁcients

in (Zhang, 2000).

5 CONCLUSION

We proposed a novel camera calibration method us-

ing concentric circles. An algorithm for estimat-

ing the projected center of concentric circles with-

out using any radii information was developed. A

method for ﬁnding the vanishing line of a circle and

the corresponding ICP’s was proposed. The calibra-

tion process does not require any measurements of the

planar pattern; thus any natural pattern of concentric

A NOVEL APPROACH TO PLANAR CAMERA CALIBRATION

circles can also be used as a calibration object. Ex-

periments with simulated data as well as real images

showed the insensitivity of the algorithm to varying

levels of noise. The estimated intrinsic parameters

had low mean errors and standard deviation. Increas-

ing the number of images beyond the minimum value

of 3 resulted in a decrease in standard deviation of the

errors.

REFERENCES

Abad, F., Camahort, E., and Vivo, R. (2004). Camera cali-

bration using two concentric circles. In International

Conference on Image Analysis and Recognition, vol-

ume 3211, pages 688–696.

Chen, Z. and Huang, J. (1999). A vision-based method for

the circle pose determination with a direct geometric

interpretation. In IEEE Transactions on Robotics &

Automation, volume 15, pages 1135–1140.

Fitzgibbon, A., Pilu, M., and Fisher, R. B. (1999). Di-

rect least square ﬁtting of ellipses. In IEEE Trans-

actions on Pattern Analysis & Machine Intelligence,

volume 21.

Grosky, W. and Tamburino, L. (1990). A uniﬁed approach

to the linear camera calibration problem. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

12:663–667.

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-

etry in Computer Vision. Cambridge University Press.

Heikkila, J. (2000). Geometric camera calibration using cir-

cular control points. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 22:1066–1077.

J.L.Mundy and A.Zisserman, editors (1992). Geometric In-

variance in Computer Vision. MIT Press.

Kanatani, K. and Liu, W. (1993). 3d interpretation of con-

ics and orthogonality. CVGIP: Image Understanding,

58:286–301.

Kim, J. S., Kim, H. W., and Kweon, I. S. (2002). A camera

calibration method using concentric circles for vision

applications. In Asian Conference on Computer Vi-

sion, volume 2, pages 515–520.

Kim, J. S. and Kweon, I. S. (2001). A new camera calibra-

tion method for robotic applications. In International

Conference on Intelligent Robots and Systems, pages

778–783.

Meng, X. and Hu, Z. (2003). A new easy camera calibration

technique based on circular points. Pattern Recogni-

tion, 36:1155–1164.

Strum, P. and Maybank, S. (1999). On plane based camera

calibration: A general algorithm, singularities, appli-

cations. In Computer Vision and Pattern Recognition,

pages 432–437.

Tsai, R. Y. (1987). A versatile camera calibration technique

for high-accuracy 3d machine vision metrology using

off-the-shelf tv cameras and lenses. IEEE Journal of

Robotics and Automation, 3:323–344.

Yang, C., Sun, F., and Hu, Z. (2000). Planar conic based

camera calibration. In International Conference on

Pattern Recognition, volume 1, pages 1555–1558.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22:1330–1334.

VISAPP 2006 - IMAGE FORMATION AND PROCESSING