PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES

USING A PSEUDOCOLOR FUZZY HOUGH TRANSFORM FOR

ARC DETECTION

Marta Penas, Manuel G. Penedo, Noelia Barreira

Dpt. Computer Science. Universidade da Coru

Campus de Elvi

na S/N. 15071, A Coru

na. Spain

Mar

ıa Jos

e Carreira

Dpt. Electronics and Computer Science. Universidade de Santiago de Compostela

Campus Sur. 15782, Santiago de Compostela. Spain

Keywords:

Perceptual primitives, Gabor wavelets, growing cell structures, chromaticity diagram, Hough transform.

Abstract:

This paper describes a computational framework for extracting the low-level directional primitives present in

an image and organizing them into circular arcs. The system is divided into three stages: extraction of the

directional features through an efﬁcient implementation of the Gabor wavelet decomposition, reduction of the

high dimensional Gabor results by means of growing cell structures and detection of the circular arcs by means

of a pseudo-color Fuzzy Hough Transform.

1 INTRODUCTION

The boundaries of objects in an image often lead

to oriented and localised changes in intensity called

edges. Edge, segment and arc detection are the ﬁrst

steps in many image analysis applications and they

are of great importance as they constitute the basis

for higher level analysis. It has always been a fun-

damental problem in computer vision that the higher

level processing stages suffer due to either too little or

too much data from the lower levels of the processing.

Thus, the quality of data available for further analysis

is very critical.

This paper describes a framework for the extrac-

tion of the directional properties present in an image

through Gabor wavelet decomposition (Gabor, 1946)

and the detection of the circular arcs that approximate

these properties through a circle detector based on the

fuzzy Hough transform (Duda and Hart, 1972).

The Gabor wavelet decomposition framework pre-

sented here is a computationally expensive process,

but provides precise information about the image

pixel orientations and is independent of the image

type. Moreover, we have implemented (M. Penas and

Penedo, 2003a) an approximation to Gabor wavelets

that reduces the computational time and memory re-

quirements through the use of a Gabor decomposition

in the spatial domain, which is faster than conven-

tional frequency domain implementations.

A previous paper (M. Penas and Mari

no, 2005) de-

scribes a line segment detector based in the combi-

nation of a pseudo-colour Hough transform and the

Burns segment detector. The fuzzy Hough transform

works properly in simple images that only contain the

objects to detect, but has some limitations in complex

images due to its global nature. Due to this limita-

tions, we have proposed a reﬁnement of the pseudo-

colour Hough transform through the introduction of

some principles of the Burns segment detector.

This paper introduces the pseudo-colour fuzzy

Hough transform for the detection of circular arcs.

These circular arcs could be combined with the line

segments previously detected in a perceptual group-

ing framework that integrated the relationships of-

fered by the Gestalt psychology (parallelism, continu-

ity, similarity, symmetry, common region and closure)

among input tokens to form large groups that could be

useful for object detection or image classiﬁcation.

2 EXTRACTION OF

DIRECTIONAL PRIMITIVES

This section contains a brief introduction of the ﬁrst

stages of the process, the extraction of the direc-

tional primitives present in the image through Gabor

wavelet decomposition and the organisation of these

results through a growing cell structure. These stages

construct the pseudo-colour images that the circular

434

Penas M., G. Penedo M., Barreira N. and José Carreira M. (2006).

PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH TRANSFORM FOR ARC DETECTION.

In Proceedings of the First Inter national Conference on Computer Vision Theory and Applications, pages 434-439

DOI: 10.5220/0001363004340439

 SciTePress

arc detector will receive as input.

Gabor wavelets (Gabor, 1946) are complex expo-

nential signals modulated by Gaussians with two im-

portant properties that make them good edge detec-

tors: the optimisation of edge localisation (Deemter

and Buf, 2000) and the absence of image-dependent

parameter tuning. Their most important drawback

is their greedy demand for both memory and com-

putation time. In a previous paper (M. Penas and

Penedo, 2003b), we developed a more efﬁcient, multi-

resolution spatial domain implementation of the Ga-

bor wavelet decomposition based on the convolution

of 11 1D-component masks obtained through the de-

composition of the 2D masks that deﬁne the wavelets.

This implementation uses the good edge localisation

property of Gabor wavelets, with the exact position of

an edge determined as a conjunction between a max-

imum in the modulus and a zero crossing in the even

or the odd part of the Gabor results.

In our Gabor decomposition, the input image is ﬁl-

tered with a bank of 8 ﬁlters centred at frequency

and 8 orientations (

kπ

,k =0..7) leading to 8 re-

sulting images. A reduction of this output space di-

mensionality is necessary in the interest of efﬁciency.

Auto-organised structures are a suitable instrument to

achieve this dimensionality reduction as they allow

the reduction of the input space and the projection of

the topological order in the input space to the output

structure, simultaneously.

Figure 1: Left: Colourmap circle inside the RGB triangle.

Right: All orientations after the GCS analysis.

Self-organised maps, growing cell structures and

growing neural gas structures were investigated and

compared for their power of dimensionality reduc-

tion of Gabor decomposition results (M. Penas and

Penedo, 2001). Growing cell structures (GCS)

(Fritzke, 1994) provided signiﬁcantly better results.

They are artiﬁcial neural networks based on self-

organised maps that eliminate the restrictions of the a

priori network size deﬁnition, incorporating a mech-

anism to add new processing elements when needed,

while maintaining the network topology.

To represent the different directionalities provided

by the auto-organised structure, each processing ele-

ment was assigned a colour from a colourmap to indi-

cate its orientation. The colourmap was obtained from

8 equidistant points on the perimeter of the maximum

circle inside the RGB triangle in the chromaticity di-

agram (Wyszecki and Stiles, 1982), centred at white

(see ﬁg. 1-left). These 8 points represent the colours

assigned to the 8 main orientations considered. Points

in the perimeter of the circle show the colour gradua-

tion assigned to the processing elements in the GCS.

Fig.1 right shows the GCS output from a ring demon-

strating the colours of the entire direction space, i.e.

0 − 2π.

Fig. 2 shows the results from three input images

that contain multiple circular arcs. The ﬁrst column

shows the original images and the second column the

results from GCS analysis.

Figure 2: Left: images ’bicycle’, ’face’ and ‘cells’. Right:

results of GCS analysis.

3 CIRCULAR ARC DETECTION

THROUGH THE HOUGH

TRANSFORM

The Hough transform is widely used in Computer Vi-

sion and Pattern Recognition for the detection of geo-

metrical shapes that can be deﬁned through paramet-

ric equations. Traditional Hough transform imple-

mentations are based on the results obtained by clas-

sical edge detectors, like Canny or Sobel. This paper

describes the design and implementation of a fuzzy

Hough transform based on the pseudo-colour images

obtained from previous processes, this is, colour im-

ages where each colour represents an orientation.

PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH

TRANSFORM FOR ARC DETECTION

435

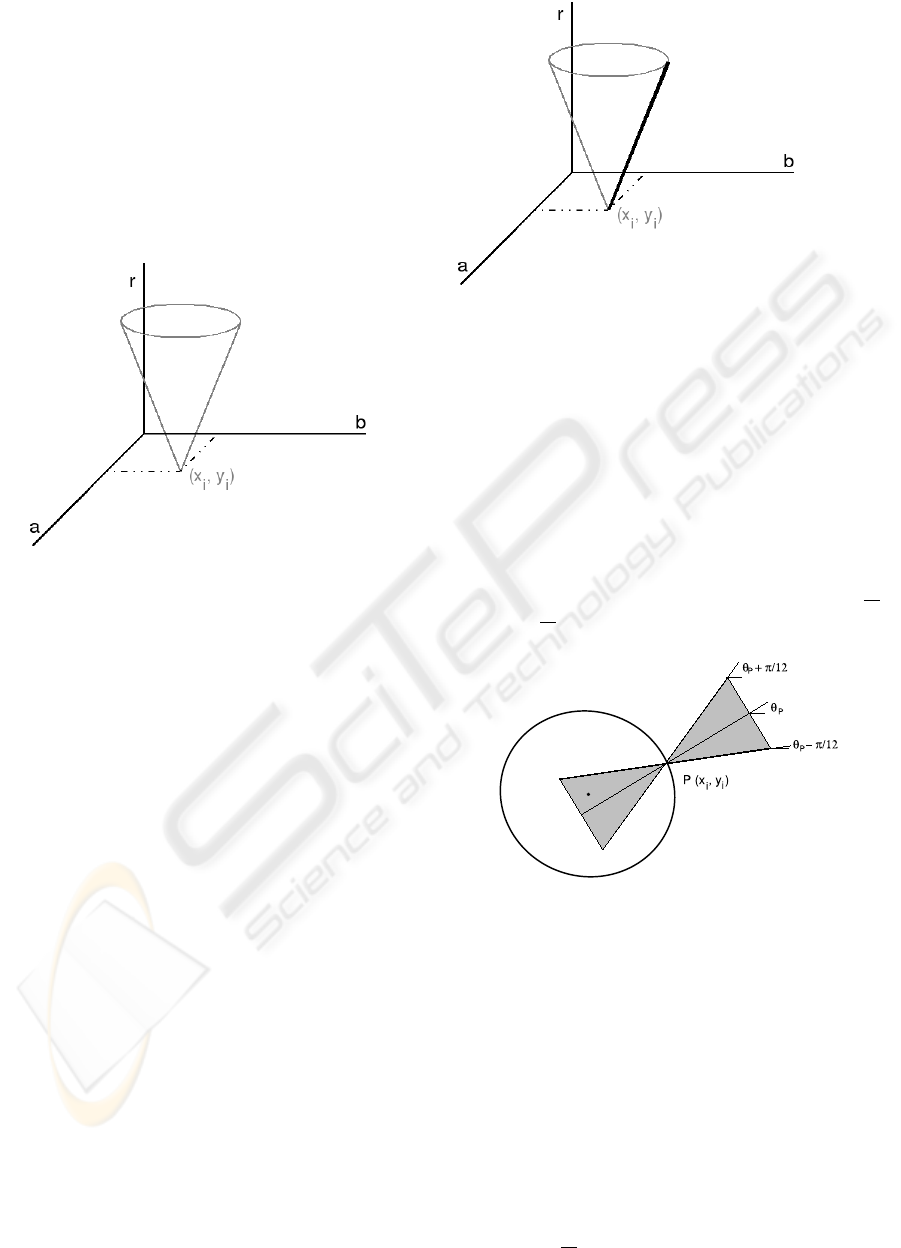
The Hough transform for circle detection is based

on the parametric equation of the circle, deﬁned as:

− a)

+(y

− b)

= r

(1)

where (a, b) are the coordinates of the circle centre

and r is the radius. The implementation of the Hough

transform in a digital computer requires the quantisa-

tion of the continuous a − b − r space into suitable

sized (a ×b ×r) cubes and the association of

each of these cubes with a cell of a 3D accumulator

array A of (N

× N

) size.

Figure 3: 3D voting space of the standard Hough transform

for circle detection.

In the standard Hough transform, each edge pixel

) votes for all the possible circles that pass

through it. This voting process generates a 3D cone

as depicted in ﬁg. 3. This approach needs to be en-

hanced to deal with the edges in our colour-labelled

images, where the colour of a pixel represents the ori-

entation of its normal line an determines where the

centre of the circle must be located. Therefore, the

voting space of a pixel (x

) is reduced to the line

depicted in ﬁg. 4. Thus, the use of the orientational

information highly reduces the computational com-

plexity of the process.

Due to the multiplicity of the edges in the pseudo-

colour images and the inaccuracies in the edge loca-

tion and orientation, we have implemented a fuzzy

Hough transform where each pixel votes, not only for

the orientation deﬁned by its colour, but also for the

adjacent orientations.

3.1 Fuzzy Hough Transform for

Circle Detection

The process begins with the quantisation of the Hough

space into (N

× N

) cells, where N

= I

, N

= min(I

) and (I

) are the

dimensions of the input image. As previously men-

tioned, each cell is assigned to a position in a 3D ac-

cumulator array A. In this quantisation, a = b =

Figure 4: The line on the cone’s surface is the voting space

of the pseudo-colour Hough transform.

r =1in order to achieve the maximum precision

possible.

Then, the contribution of each pixel P =(x

)

to the accumulator array is computed. First, the angle

of the pixel is determined from its colour. Then,

the voting space of the pixel is constructed. In the

fuzzy Hough transform, each pixel votes for the set of

centres and the corresponding radios contained in the

grey area depicted in ﬁg. 5. This area is delimited by

the two lines that pass through P with slopes θ

and θ

−

and by the maximum radius stipulated.

Figure 5: Voting space of pixel P in the pseudo-colour

fuzzy Hough transform for circle detection.

The contribution of the pixel P to the accumula-

tor array is not homogeneous for all the (a − b − r)

in ﬁg. 5. It is maximum over the line that passes

through P with slope θ

and decrease with the ori-

entation difference. Speciﬁcally, the contribution is

deﬁned through the following Gaussian function:

A(a

)=e

−β·d(θ

,θ

)

(2)

where the parameter that deﬁnes the decay of the

Gaussian function β is set to 10, as the contribution to

the accumulator array must rapidly decrease with the

orientation difference, falling to the minimum when

d(θ

,θ

VISAPP 2006 - IMAGE ANALYSIS

436

Once the voting process has ﬁnished, the following

step is the detection of maxima. Each maximum de-

tected in the accumulator array corresponds to a cir-

cle in the image that can contain one or more arcs.

For each maximum over a predeﬁned threshold, an in-

verse Hough transform takes place removing the con-

tributions to the accumulator array of the pixels be-

longing, not only to the circle detected, but also to

the concentric neighbouring ones. The detection of

arcs takes place simultaneously to the inverse Hough

transform. When a pixel is removed from the accu-

mulator array, its orthogonal projection to the circle it

belongs to is determined. Once all the pixels involved

have been analysed, the circle is sequentially searched

determining which pixels have been coloured and thus

belong to an arc.

Fig. 6 right shows the circle detection results over

the images depicted in ﬁg. 6 left.

Figure 6: Left: input images. Right: results of the arc de-

tection process with the fuzzy Hough transform.

The implementation just described accurately de-

tects the centres and radius of the circles but has two

important drawbacks, the computational complexity

and the memory elapsed. Next section describes

a probabilistic implementation of the fuzzy Hough

transform that reduces the computational complexity

at the expense of reducing the quality of the results.

3.2 Probabilistic Fuzzy Hough

Transform for Circle Detection

The probabilistic Hough transform (Goulermas and

Liatsis, 1999) is based on the possibility of detecting

the circles in an image through the analysis of a lim-

ited subset of the edge points. It is also based in the

following property depicted in ﬁg. 7: if A and B are

two points belonging to a circle, the normal lines that

connect them with the centre of the circle and the per-

pendicular bisector of the segment that joins them in-

tercept in the centre of the circle.

Figure 7: Property that relates two points that belong to a

circle.

Due to the innacuracies in the orientation estima-

tion and the effect of the discretization necessary in

the digital images, each point votes not only for the

radius and centre determined by the intersection of the

normals and the perpendicular bisector, but for those

in the voting space depicted in ﬁg. 8. This voting

space consists of a line segment that belongs to the

perpendicular bisector and is delimited by the maxi-

mum radios allowed and/or the voting spaces of the

fuzzy Hough transform for circle detection in points

A and B, respectively.

Figure 8: Probabilistic fuzzy Hough transform. The voting

space is the dotted line segment enlarged on the right of the

ﬁgure.

The operation of the algorithm is divided into two

phases, the voting and the search for maxima in the

accumulator array. The voting begins with the ran-

dom selection and storage in a list L of a small per-

centage n (≈ 5% of N ) of the N edge points. Then,

for each of the K =

n·(n−1)

combinations of point

pairs, the voting space is computed and the correspon-

ding cells in the accumulator array are incremented.

PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH

TRANSFORM FOR ARC DETECTION

437

As in the fuzzy Hough transform, the contribution to

the accumulator array is not homogeneous and de-

pends on the orientation distance (see eq. 2).

Once the voting process has ﬁnished, the search

for maxima in the accumulator array begins. Each

maximum detected represents a candidate circle in the

image but, as only a small subset of points has voted,

in order to check the existence of the circle, the in-

verse Hough transform must calculate the percentage

of edge points that belong to the circle detected. Only

if this percentage is over a predeﬁned threshold, the

candidate is considered a circle.

If the candidate is considered a circle, all the points

that belong to it are deleted from the edge image and

the accumulator array, the list L is updated up to its

original size n with points chosen at random and the

next maximum is analysed. If the circle is not valid,

a predeﬁned number of points t (t ≈ 20% of n) are

erased and the same number of new points are in-

serted into L. The points erased are those that less

contributed to the accumulator array. The algorithm

stops when three non-valid circles are consecutively

detected.

Fig. 9 left shows the results obtained from the three

input images depicted ﬁg. 9 right.

Figure 9: Left: input images. Right: results of the arc de-

tection process with the probabilistic Hough transform.

The probabilistic fuzzy Hough transform has

an important advantage with respect to the non-

probabilistic fuzzy Hough transform, the high com-

putational complexity reduction. But it also has some

important drawbacks. The ﬁrst one is due to the use

of a small subset of points, which leads to inaccura-

cies in the results specially when the image contains

circles with very different sizes. Also, as the points

are randomly chosen, the results can vary among the

executions. Finally, the probabilistic Hough trans-

form works with combinations of pairs of points, if

the sample of points analysed has to be renewed many

times during the execution, the computational time

can exponentially grow.

In order to improve the results of the probabilis-

tic fuzzy Hough transform and to reduce the com-

putational complexity of the fuzzy Hough transform,

some basic principles from both implementations

have been combined in a new probabilistic fuzzy

Hough transform.

This implementation of the Hough transform is

very similar to the fuzzy Hough transform introduced

in sec. 3.1 but only a determined percentage N of

the input edge points is analysed. The sample points

are not randomly chosen, but homogeneously selected

from the input image. Empirically, we have checked

that a percentage of N ≥ 33% of the edge points pro-

duces good results.

The voting process of the sample points is analo-

gous to the one described in sec. 3.1 for the fuzzy

Hough transform. The voting process is followed by

the search for maxima in the accumulator array. As

in the probabilistic fuzzy Hough transform previously

described, each maximum detected represents a pos-

sible circle in the image but, as only a small subset

of points has voted, in order to check the existence of

a circle, the inverse Hough transform must compute

the percentage of edge points that belong to the circle

detected. Only if this percentage is over a predeﬁned

threshold, the candidate is considered a circle.

Fig. 10 right shows the arc detection results from

the three input images depicted in ﬁg. 10 left. These

results are very similar to those obtained by the fuzzy

Hough transform (ﬁg. 6 right) while the computa-

tional complexity of this implementation is consider-

ably lower.

4 DISCUSSION AND

CONCLUSION

This paper describes a computational framework for

the detection of circular arcs in 2D digital images.

The framework is divided into three stages: the direc-

tional primitive extraction through Gabor wavelets,

the organisation of these primitives through auto-

organised structures and the circle detection through

a probabilistic fuzzy Hough transform.

The pseudo-colour fuzzy Hough transform intro-

duced in sec. 3.1 produces very good results, but it

has an important drawback, the high computational

complexity. The probabilistic Hough transform in-

troduced in sec. 3.2 overcomes this drawback but

VISAPP 2006 - IMAGE ANALYSIS

438

Figure 10: First column: input images. Second column: re-

sults of the arc detection process with the new probabilistic

Hough transform.

its results are not too accurate. Finally, the proba-

bilistic Hough transform introduced at the end of sec.

3.2 produces good results while keeping the compu-

tational complexity low, through the introduction of a

new way of selecting the candidate edges.

Fig. 11 shows the computational time (in minutes)

of the three versions of the Hough transform descri-

bed in this paper. The data depicted in ﬁg. 11 have

been collected from the analysis of 10 input images

containing a different number of edge points rang-

ing from 4026 to 19227, and shows that the compu-

tational complexity depends both on the number and

the distribution of the edge points.

0 4026 5912 7613 7730 8435 10695 14450 14510 14922 19227

2,5

7,5

12,5

17,5

22,5

27,5

32,5

Fuzzy Hough

transform

Subsampled

probabilistic fuzzy

Hough transform

Probabilistic fuzzy

Hough transform

Number of edge points

Computational time (min)

Figure 11: Computational times of the alternative versions

of the fuzzy Hough transform.

The three implementations could be improved

through the use of directional information. The

pseudo-colour images that the fuzzy Hough transform

receives as input contain information about the orien-

tation of the edges, but not about their direction. The

directional information could be introduced through

the application of a Sobel ﬁlter to the pseudo-colour

edge images, where the noise presence is almost null.

The use of directional information could reduce the

computational complexity of the three implementa-

tions and increment the accuracy of the probabilistic

ones.

ACKNOWLEDGEMENTS

This paper has been partly supported by the Xunta de

Galicia through grant PGiDT03TIC10503PR.

REFERENCES

Deemter, J. V. and Buf, J. D. (2000). Simultaneous detec-

tion of lines and edges using compound Gabor ﬁlters.

Journal of Pattern Recognition and Artiﬁcial Intelli-

gence, 14(4):757–777.

Duda, R. and Hart, P. (1972). Use of the hough transform

to detect lines and curves in pictures. Comm. ACM,

15:11–15.

Fritzke, B. (1994). Growing cell structures - a self-

organizing network for unsupervised and supervised

learning. Neural Networks, 7(9):1441–1460.

Gabor, B. (1946). Theory of communication. Journal of the

Institute of Electronic Engineers, 36(93):429–457.

Goulermas, J. and Liatsis, P. (1999). Incorporating gradi-

ent estimations in a circle-ﬁnding probabilistic hough

transform. Pattern Analysis and Applications, 2:239–

250.

M. Penas, M. J. C. and Penedo, M. G. (2001). Auto-

organised structures for extraction of perceptual prim-

itives. Lect. Notes Comp. Science, 2085:628–636.

M. Penas, M. J. C. and Penedo, M. G. (2003a). Ga-

bor wavelets and auto-organised structures for direc-

tional primitive extraction. Lect. Notes Comp. Sci-

ence, 2652:722–732.

M. Penas, M. J. C. and Penedo, M. G. (2003b). Perceptual

organization of directional primitives using a pseudo-

color hough transform. Lect. Notes Comp. Science,

2749:893–898.

M. Penas, M. J. Carreira, M. P. and Mari

no, C. (2005). Seg-

ment extraction using burns principles in a pseudo-

color fuzzy hough transform. Lecture Notes Comp.

Science, 3523:175–182.

Wyszecki, G. and Stiles, W. S. (1982). Color science,

concept and methods, quantitative data and formulae.

John Wiley & sons.

PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH

TRANSFORM FOR ARC DETECTION

439