HUMAN BODY TRACKING FOR PHYSIOTHERAPY VIRTUAL

TRAINING

Sara Shafaei, Mohammad Rahmati

Computer Engineering Dep.,Amirkabir University of Technology (Tehran Polytechnic),

Hafez Ave, No 424, P.O.BOX 15875-4413 Tehran, Iran

Keywords: Human motion tracking, virtual training, physiotherapy, machine vision

Abstract: In this paper, we introduced a system in which it can be used for patients who are prescribed to undergo a

physiotherapy treatment. In this personal virtual training system we employ several markers, attached to the

various points of the human body. The system provides a physiotherapy session to the user, once the session

is repeated by the user, the video image sequence captured by the system is analyzed and results are

displayed to the user for further instructions. Our design consists of 3 general stages: detection, tracking,

and verification stages. In the detection stage, our aim is to process the first frame of the image sequence for

detecting the locations of the markers. In order to reduce the computational complexity of the first stage, the

detection was performed in the lower scale of a Gaussian pyramid space representation. The second stage of

our system performs tracking of detected markers of the first stage. A prediction algorithm is applied in this

stage in order to limit the search along the predicted directions during the search for the markers in

subsequent frames. For verification stage, the trajectory of the markers will be compared with the

information in the model. Trajectory matching is performed by computing the difference between their

smoothed zero-crossing potentials of the captured trajectory and the model.

1 INTRODUCTION

Human motion analysis by computer has become an

important research issue in different areas of

medicine and human science. In clinical gait

analysis, for example, the temporal information

about the position and orientation of the patient’s

joints may be useful in determining abnormalities

(Yeasin ,2000). In orthopedics, the range of motion

information helps in the evaluation of the prosthetic

join replacement and physical therapy of joint

disease (Richards,1999). Postural analysis during

human motion can be studied from the

representation of the column through the position of

the markers fixed to the spinal process

(Crosbie,1997). Athletic performance can also be

improved by breaking down the movement into

elementary components and by identifying suitable

reference models arising from the observation of the

outstanding athletes (Pedotti,1983).

For these reasons, there is a great interest in

developing measurement techniques that allow a

more accurate and automatic analysis of the human

movement. In particular, systems based on markers

and cameras, have been extensively used to record

kinematics of the human motion (Richards,1999).

Markers can be defined as special objects that are

attached or fixed to the human body, helping to track

the movement of important points.

In this paper, we present the design and

implementation of a virtual personal physiotherapy

trainer prototype using markers to improve the

results. This system establishes a personalized

physiotherapy session for the user and displays the

resulting instruction on a monitor. The user

periodically receives visual feedback from the

virtual instructor on how he/she is currently doing.

To accomplish this, we use a video camera in the

room and incorporate various real-time computer

vision techniques. Following presentation of a

movement by an instructor, the patient repeats the

movement accordingly. By capturing the video

sequence of the trainee the task of the system is to

recognize the physiotherapy movement of the user

using the output of the vision system. In order to

improve the performance of our system user needs

to wear 12 markers. A cartoonish-like characters

maybe used as the virtual instructors, but in this

449

Shafaei S. and Rahmati M. (2006).

HUMAN BODY TRACKING FOR PHYSIOTHERAPY VIRTUAL TRAINING.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 449-454

DOI: 10.5220/0001364704490454

 SciTePress

system we chose to use stored movie clips for

simplicity. While we use only one instructor it

might be more instructors involved. We currently

have twelve physiotherapy moves used in our

system.

Currently, a set of movie clips, showing a full

view of the instructor, is used. In each clip the

instructor performs a single cycle of the move then

visual feedback of the instructor is displayed. In our

proposed system if the algorithm recognizes that the

user is performing the physiotherapy move correctly,

it notifies the user that he performs complete

movement correctly and if the user movement is

wrong, system notifies the user that his movement is

wrong and along with the information that which

part of the body had wrong movement.

Our design is divided into the following three

procedures: 1. Detection of the markers in the first

frame. 2. Tracking markers in the rest of the frames

and finding the trajectories 3. Matching motion

trajectories with stored model.

The paper is organized as follows. In section 2

we introduce, without going into the details, the

pervious systems related to human movement

analysis. In Section 3 we described the method that

was used for detection of markers in the first frame,

and in Section 4 we explain how to track markers in

a video sequence and this is divided into two

procedures: matching and prediction. The matching

is used to find correspondence between the extracted

objects of two consecutive frames. The prediction

stage is an important stage in order to limit the

search region, thus reducing the execution time. In

Section 5 the verification of the trajectories,

recorded from markers movements, will be

discussed and they are compared with the

information for the models. Comparison between a

trajectory and the model is performed by computing

the difference between their smoothed zero-crossing

potentials. Our experimental results are in Section 6

and conclusion is in Section 7.

2 PREVIOUS SYSTEM

A system called W4 ( Haritaoglu,1998) is a real time

visual surveillance system for detecting and tracking

people and monitoring their activities in an outdoor

environment. It operates on monocular grayscale

video imagery, or on video imagery from an infrared

camera.

Other system called Pfinder (Wren ,1997) is a

real-time system for tracking a person which it uses

a multi-class statistical model of color and shape to

segment a person from a background scene. It finds

and tracks people’s head and hands under a wide

range of viewing condition.

System introduced by Kidrooms (Bobick,1996)

is a tracking system based on “closed-world

regions”. These are regions of space and time in

which the specific context of what is in the regions

is assumed to be known. These regions are tracked

in real-time domains where object motions are not

smooth or rigid, and where multiple objects are

interacting.

3 DETECTION

As mentioned earlier, there are 12 markers; as

shown in Figure 2; these are used to locate important

human body points. Detection of markers in the first

frame is an important step in our proposed system.

We used a Gaussian Pyramid representation in order

to decrease computational processing time. Each

level of a Gaussian pyramid is a lower resolution

with respect to the previous one. In each level we

simply performed two operations: 1) low-pass filter

of the image, and 2) discarding the odd numbered

rows and columns from the filtered image. These

operations performed for both of input image and

template image. Low-pass filtering of input image is

accomplished by taking a weighted average of a 5x5

region surrounding at each image pixel. To increase

computation efficiency, a separable equivalent

weighting function was used to perform the 5x5

weighted averages. At first, convolving an image

with a 1x5 weighting function, the 'horizontal'

weighted average of the image is obtained. Next,

convolving the horizontally averaged result with the

transpose of the 1x5 vector (i.e. a '5x1') weighting

function results the 'vertical' weighted averaging. A

Gaussian-like weighting function with values of [.05

.25 .5 .25 .05] was used as the impulse response of

our filter. Due to our input image frame size, we

used the two-level pyramid in our system. As an

example, a frame of video sequence in the original

size and its lower resolution is shown in the Figure

Once the resolution of an image and the template is

decreased, using Gaussian pyramid at one level, then

a template representing a marker must be searched

in the lower level. When located, then we find the

probable locations of the markers within the 2x2

region surrounding the places found in the

corresponding locations of the original image. The

cross-correlation function is used for detection,

given by the following relationship.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

450

)),(()),(),((

)),())(,(),((

∑∑∑∑

∑∑

−=−=−=−=

−=−=

−−++

hnmhjifnjmif

(1)

where

is the cross correlation value at (i,j)th

location between function f(,), the color image for

original image and gray image for lower level image

in the searched region, and h(,), the model of the

marker with (2M+1)× (2N+1) pixels. The values

and

are the mean of f and h, respectively. In

Figure 3, detection of markers in one of our

experiments at low and high resolutions is shown.

(a) (b)

Figure 2: (a) lower resolution (b) Original image.

(a) (b)

Figure 3: (a) marker found in lower resolution (b)

Location of marker found at original image shown with

squares.

4 TRACKING

Tracking the motion of human's parts, in a sequence

of images, is an important step in automatic analysis

of the human movement. This is a challenging

problem due to non-rigidity of the human body, the

influence of the environment, and other constraints.

The automatic tracking can be used in a variety of

applications, such as clinical gait analysis

improvement of the human performance in sports,

ergonomics, and so on. This involve in two parts,

matching and prediction.

4.1 Matching

Matching is referred to as steps necessary to find the

correspondence of markers between 2 consecutive

frames. The matching between a marker model and

its corresponding within an image is based on the

gray-scale values of the pixels and it is evaluated by

the Mean Absolute Difference (MAD) function

between the marker model and a portion of the

image within the search region. The template

matching is accomplished by locating the points

where MAD between the image and the model is

minimized. In this way, the computation complexity

is highly reduced. The MAD at (i, j)th location is

defined as

|)),(),((| nmhnjmifD

∑∑

−=−=

−++=

,(2)

Where f is input image within the search area and

h is the pixel value of the model representing the

marker of size (2M+1)× (2N+1) pixels. The

location with minimum value is location of marker.

4.2 Prediction

The matching function is applied to the significant

regions extracted from the segmentation algorithm

in the prediction step. This local aspect reduces the

processing time of the matching step. Of course,

regions with high correlations are selected

corresponding to the expected position of the

markers.

In order to reduce the search region, it is

necessary to define a mechanism to predict the

possible positions of the markers at the successive

frames. For this purpose, we can use a simple

extrapolation function. This can be done by a rough

prediction, according to the following extrapolation

function:

)57(

21 −−

+−=

kkkc

xxxx

)57(

21 −−

+−=

kkkc

yyyy

, (3)

HUMAN BODY TRACKING FOR PHYSIOTHERAPY VIRTUAL TRAINING

451

where

x and

y are the spatial location of the

current markers point for the kth frame, and

x ,

represent the center of the searching region for the

(k+1)th frame, after finding

x ,

y We searched

region around

x ,

y with radius 7 pixel for finding

marker. In fact region size for markers searching is

15*15 pixels. We determined this region size from

several experiments.

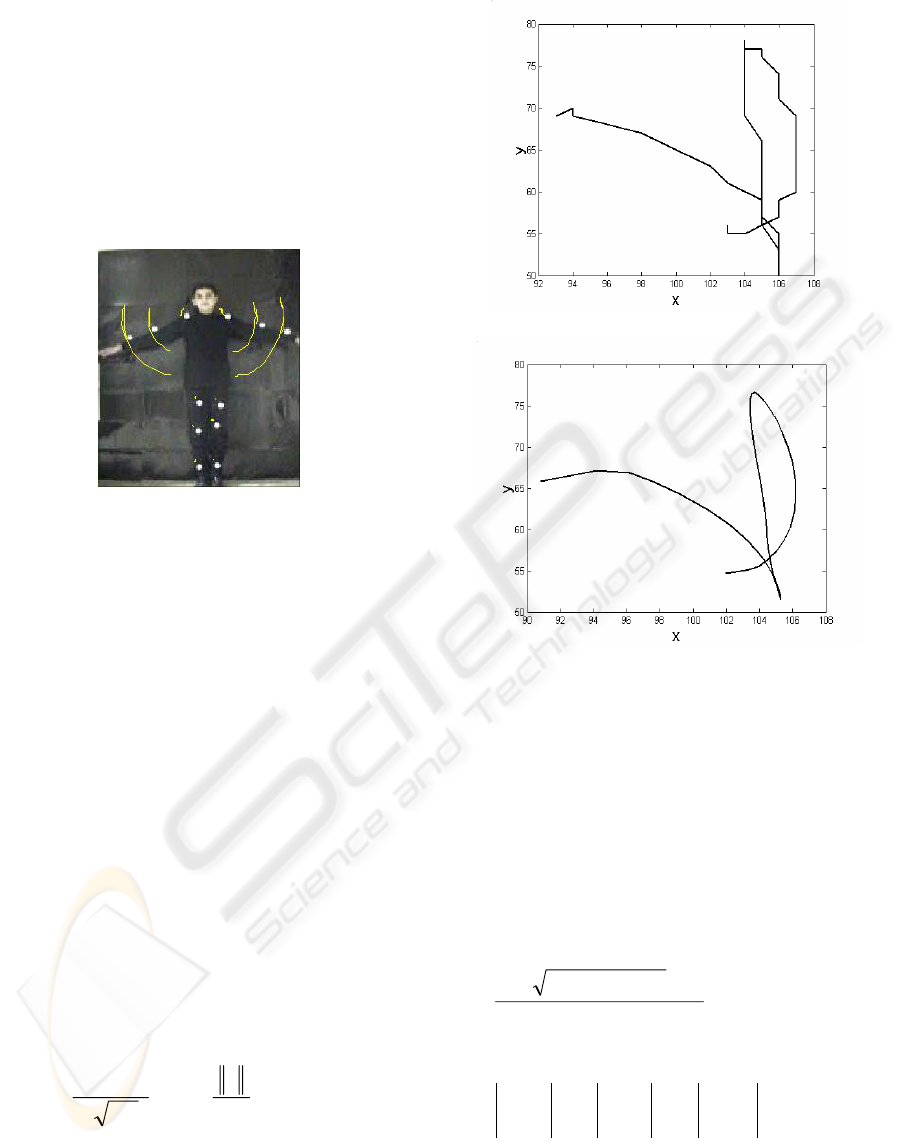
Figure 4 : Trajectory of motion after tracking.

5 VERIFICATION OF MOTION

5.1 Smoothing Trajectory

A trajectory is a spatio-temporal curve defined as:

(x[1],y[1], 1), (x[2], y[2], 2),…, (x[n], y[n], n) where

x[n],y[n] are coordinate value of a marker in frame

n. There are essentially two 1-D functions involved:

x[n] and y[n] in the above definition of a trajectory.

A trajectory for a specific action performed in one of

our demonstration is shown in the Figure 4 and its

temporal function is shown in Figure 5b. This

trajectory contains some noise due to errors during

tracking. In order to deal with this noise, we use a

Gaussian kernel as defined below, and apply it to the

noisy signal to smooth x[n] and y[n] coordinates of

the trajectory. We convolve trajectory with

Gaussian kernel described by equation given below.

For our experiments s =2 was selected. Result of

smoothing is shown in the Figure 5a.

)

exp(

)2(

)(

−=

(4)

(a)

(b)

Figure 5 : (a) noisy trajectory of marker (b) Smoothed

trajectory of marker.

5.2 Spatio-temporal Curvature

Parameterization

We use spatio-temporal curvature (Cedras, 1995) to

represent an action. In this case, a 1D version of a

quadratic surface fitting procedure is used. The

spatio-temporal curvature, represented by k, is

computed as follows:

2/3222

222

))()()(( zyx

CBA

′

, (5)

Where

′′′′

′′

′′′′

′

′′′′

′

= ,,

where the notation |·| represents the determinant

of a matrix. The first and second derivative of a

function x(t) is denoted by

)1()()(

−

−=

′

txtxtx

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

452

)1()()( −

′

−

′

′′

txtxtx

, respectively. Since the time

interval is constant, so

′

, and t" = 0.

The spatio-temporal curvature has the advantage

over other trajectory parameterizations since it

captures both the speed and direction changes in one

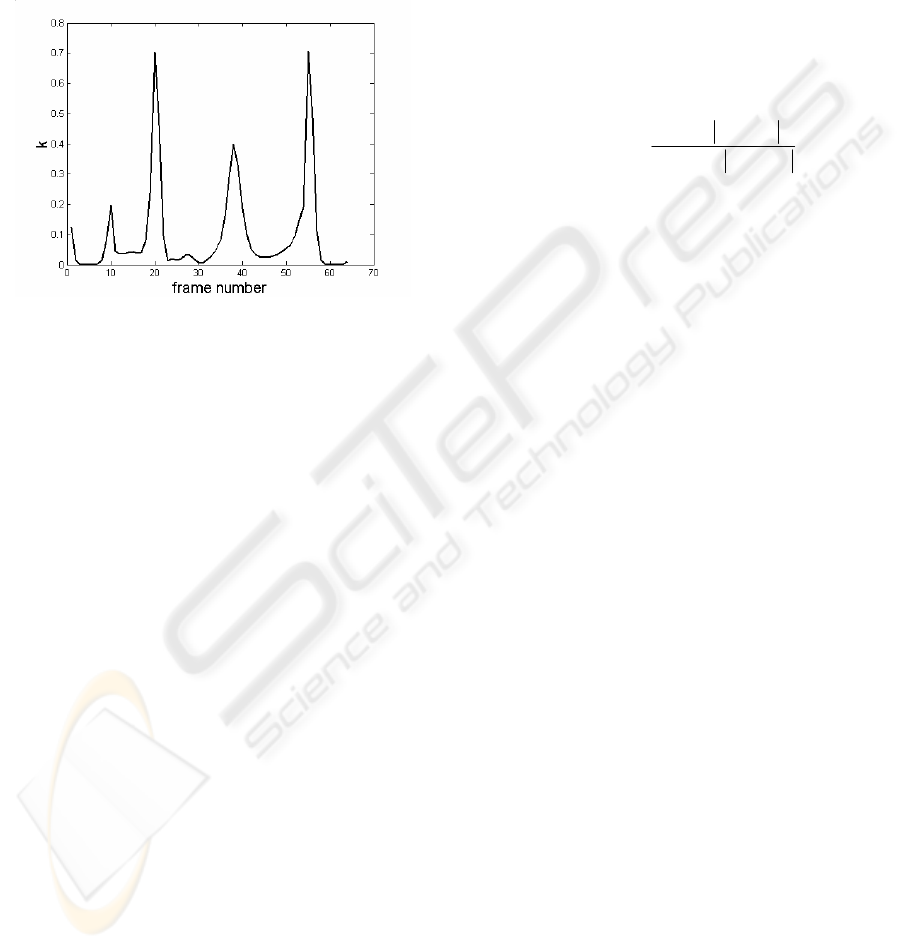
quantity. Figure 6 depicts the spatio-temporal

curvature for a trajectory as captured from Figure 5.

Figure 6: Spatio-temporal curvature for trajectory Figure

5.3 Matching Trajectory

There are twelve trajectories related to the twelve

markers which will be compared with the stored

information of the model. A match score for each

marker is produced which indicates how closely the

two trajectories matched.

Matching between two trajectories is evaluated

by computing the difference between their smoothed

zero-crossing potentials, and employing the idea of (

Rangarajan,1993) for matching the scale-space

representation. The first step in this algorithm is to

decompose the trajectory into 1D signal, the spatio-

temporal curvature that was explained in the

pervious section. The scale-space is computed by

repeatedly convolving the input spatio-temporal

curvature signal with second derivative of Gaussian

mask with various σ values. The output is then

checked for zero-crossings, the indicative of

discontinuities. The location and potential (the

absolute difference between the values where the

zero-crossing occurs) of each zero-crossing is stored

in a set of arrays, one for each σ value. The set of

arrays is organized into a two dimensional table,

with the location (frame number) as the x axis and σ

as the y axis. It is well known that the zero-

crossings of a distorted signal are dislocalized and as

a result, the zero-crossing potentials from a distorted

signal are not the same as those from an undistorted

signal. However, a smoothed zero-crossing

potential is less sensitive to noise, so the zero-

crossing from that table are diffused by convolving

with a two dimensional Gaussian of standard

deviation equal to 1 (see figure 7). In the next step,

this array is multiplied by a scaling factor and the

results are stored as an array. The matching itself is

done by element by element subtraction operations

between the diffused input and the model in the

scale-spaces representation. The absolute values

from the subtraction are stored. In the final step, the

match score is computed using the following

equation:

∑

−=

),(*2

),(

σα

σε

scorematch

(6)

where

is the array containing the element by

element subtraction of input and model, for spatio-

temporal curvature and

represent spatio-

temporal curvature of the model. If this score is

lower than the preset threshold, we used a value of

0.7 for the threshold, then the user’s motion is

wrong, otherwise it is right. The user is notified due

to the wrong joint movements.

6 EXPERIMENTS

Images of our video sequences are 144x176 pixels in

size. We have considered twelve different

physiotherapy actions performed by a user, and we

have recorded a large number of video sequences. In

Figure 8 we have shown a few frames from only 2

different moves. We have considered cases where

the markers may come very close to each other; even

in some cases we had overlaps between the markers.

We also tested the system under different speed of

body movements. Results of detection and tracking

in all actions were performed correctly and there

were no errors in the verification of all twelve

movements. Figure 8 shows sequences of two

actions. Our overall evaluation will be completed

once the system is tested with complex movements.

7 CONCLUSIONS

In this work, we introduced a system for a virtual

personal physiotherapy trainer. One of the main

advantages of this system is its comfort and

possibility of using it in personal environment for

training physiotherapy movement where the

HUMAN BODY TRACKING FOR PHYSIOTHERAPY VIRTUAL TRAINING

453

therapists is not available or patient may be at

remote area in which the expert is not readily

accessible. The important feature of the system is its

precision, and furthermore, if the user’s movement is

wrong, the system would notify the user of the error

and advise the patient, that which part of the

movement was wrong.

(a)

(b)

(c)

Figure 7: (a) Scale-space of spatio-temporal of trajectory a

sample and reference motion (b) Zero-crossing potential

of the spatio-temporal curvature scale-space of trajectory a

sample and reference motion (c) The diffused zero-

crossing potential of the spatio-temporal curvature scale-

space of trajectory a sample and reference motion.

(a) (b) (c) (d)

Figure 8 : video sequences of four actions .There are 60

frames in each sequence . (a) frame 1 (b) frame 10 (c)

frame 40 (d) trajectory of markers.

REFERENCES

Bobick A. and Davis J. and Intille S. and Baird F. and

Cambell L. and Irinov Y. and Pinhanez C.and Wilson

A.,1996. KidsRoom: Action recognition in an

intractive story environment. M.I.T. TR , No.398.

Cedras C. and Shah M. , 1995. Motion-based

recognition: a survey, Image Vision Comput,

Vol.13, No.2 , pp.129–155.

Crosbie J. and Vachalathiti R.and Smith R., 1997. Pattern

of spinal motion during walking. Gait and Posture ,

Vol. 5, pp 6-12.

Haritaoglu I. and Harwood D. and Davis L. S.,1998. W 4 :

Who? When? Where? What? - A real time system for

detecting and tracking people. International

Conference on Automatic Face and Gesture

Recognition,Nara, Japan, pp 877-892 .

Pedotti A. and Farigo C. and Rodano R., 1983.

Optimization of motor coordination in sport an

analytical approach. Biomechanics and Performance

in Sports, Baumann,Schnordorf ,pp 145-/160.

Rangarajan K. and Allen W. and Shah M. , 1993.

Matching motion trajectories using scale-space.

Pattern Recognition, Vol. 26, No. 4, pp 595-610.

Richards J.G., 1999. The measurement of human motion:

a comparison of commercially available systems,

Human Movement Science, New York ,USA, pp 589-

/602.

Wren C.R. and Azarbayejani A. and Darrell T. and

Pentland A.P., 1997. Pfinder:real-time tracking of the

human body, IEEE Transactions on Pattern Analysis

and Machine Intelligence,Vol. 19, No. 7, pp 780-785.

Yeasin M. and Chaudhuri S., 2000. Development of an

automated images processing system for kinematic

analysis of human gait,Real-Time Imaging , Vol. 6, pp

55-67.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

454