A DETECTION METHOD OF INTERSECTIONS FOR

DETERMINING OVERLAPPING USING ACTIVE VISION

Pablo Gil, Fernando Torres

Department of Physics Engineering Systems and Signal Theory, University of Alicante, Alicante, Spain

Oscar Reinoso

Department of Industrial Systems Engineering, Miguel Hernandez University, Elche, Spain

Keywords: Discontinuities, Overlapping, Occlusion, Occluded partially objects, Structured light.

Abstract: Sometimes, the presence of objects difficult the observation of other neighboring objects. This is because

part of the surface of an object occludes partially the surface of another, increasing the complexitiy in the

recognition process. Therefore, the information which is acquired from scene to describe the objects is often

incomplete and depends a great deal on the view point of the observation. Thus, when any real scene is

observed, the regions and the boundaries which delimit and dissociate objects from others are not perceived

easily. In this paper, a method to discern objects from others, delimiting where the surface of each object

begins and finishes is presented. Really, here, we look for detecting the overlapping and occlusion zones of

two or more objects which interact among each other in a same scene. This is very useful, on the one hand,

to distinguish some objects from others when the features like texture colour and geometric form are not

sufficient to separate them with a segmentation process. On the other hand, it is also important to identify

occluded zones without a previous knowledge of the type of objects which are wished to recognize. The

proposed approach is based on the detection of occluded zones by means of structured light patterns

projected on the object surfaces in a scene. These light patterns determine certain discontinuities of the

beam projections when they hit against the surfaces becoming deformed themselves. So that, such

discontinuities are taken like zones of boundary of occlusion candidate regions.

1 INTRODUCTION

Recognition of objects in image space is not a trivial

problem. Commonly, in robotic environments,

images are taken from scene where several objects

interact together. In addition, the illumination

conditions, view points, positions and orientations of

the objects that are desired to identify can change at

every moment of time.

In this context, the objects in image space suffer

the presence of occlusions and shadows which make

difficult or prevent the recognition due to the

ambiguity of boundary between different object

surfaces, especially when free-form surfaces are

involved in the scene.

To avoid some concrete types of occlusions,

active vision can be adopted. Structured light or

pattern projection systems have been used for this

purpose.

Our method is based on the assumption that the

occlusions are not caused by lack of visibility due to

shadows or by opacity of an object which hides part

of itself due to its geometrical form. Here, we have

assumed that the occlusion is caused by overlapping,

with or without contact. On the one hand, we

consider overlapping with contact when the surface

of an object A is in contact with the surface of

another object B, and the surface of A is partially

hidden by the surface of B. And, on the other hand,

overlapping without contact is considered when the

spatial pose of each object at different depth levels

(different distance from camera used like view

point) cause that the pose of an object A prevents to

perceive another possible B correctly, because B is

in the background of the scene. In these practical

applications, it is the camera and its relative pose

which need to be online adjusted.

The objective of this paper is to find the

intersection zone among surfaces of objects. Such

501

Gil P., Torres F. and Reinoso O. (2006).

A DETECTION METHOD OF INTERSECTIONS FOR DETERMINING OVERLAPPING USING ACTIVE VISION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 501-507

DOI: 10.5220/0001364905010507

 SciTePress

intersection is caused by surfaces discontinuity

among different objects. Determining this

discontinuity, it is possible know which is the

intersection zone that delimit a possible occlusion

zone of an object hidden by another one.

This paper is organized as follows: The concept

and the types of occlusion are described in section 2,

also in this section we briefly expose the recognition

systems for occluded object presents in the literature

and which is the main problem of each system.

Section 3, show a method based on structured light

to detect occluded zones by overlapping between

objects in the image space. Our approach consists of

two steps. First, we fit the contours of beam

projection in the image with polygonal approach.

Second, it is commented a clustering process to

separate beam projection over different surfaces or

surfaces with different depth level, previously fit as

polygonal contours. The presented clustering

process combines moments and distances. To this

end, our clusters are fit afterwards by means of

straight lines. These one delimits the overlapping

zone. Section 4 gives the experimental results in the

implementation and 5 the conclusions.

2 CONCEPT AND ANALYSIS OF

OCLUSSIONS

The recognition and classification systems of objects

are based generally on the recognition from the

extraction of characteristics and properties of the

visible part of the objects (Bhanu, 2003)(Ulrich,

2001)(Ying, 2002). Therefore, the recognition

systems employed for computer vision do not often

work correctly when there are partially occluded

objects in a scene. This is because different types of

objects can be very similar if its visible part is only

observed (Figure 1).

There are different ways to classify the type of

occlusion. Depending on the cause that produces it,

the following categories can be distinguished:

• Occlusions in which an object covers a portion

of the area of other object which is wished to be

recognized and it is not absolutely visible. It is

well-known like overlapping (Boshra,

2000)(Ying, 2002).

• Occlusions by opacity. An object hides part of

itself due to its own geometry (Bhanu, 2003).

• Occlusions due to shadows. The kind of

illumination causes shadows in the image

around the object to be recognized or around the

rest of present objects in the scene. Thus, an

object can be occluded partially by its own

shadow or the shadow of other object according

to the kind of light employed (Bhanu,

2003)(Ulrich, 2001).

Almost all the recognition systems of occluded

partially objects which obtain good results of

success in the identification, are based on statistical

or stochastics methods and need a great percentage

of probability information (Park, 2003)(Ying, 2002).

Some of the techniques used in these systems

aim at the recognition of flat objects, 2D-objects or

three-dimensional ones (Chan, 2002) (Park,

2003)(Ulrich, 2001)(Ying, 2002) but whose registry

in image space and the processing employed does

not permit to work with the third dimension. In

much of these works, is not important what type of

occlusion appears, why it is caused or how it can be

avoided or corrected or where is located that

occlusion in the image. Only, the bi-dimensional

information of the visible part of the object is

analyzed and studied.

Here, a possible solution to improve the

recognition of objects with occlusions is proposed.

This one consists in determining where the occlusion

is located in image space. Thus, if the occlusion

zone is known, the camera can be repositioned with

respect to a non-planar object given to avoid or

reduce it. Furthermore, additional information about

the boundary and occlusion zones of the objects can

be important for a successful recognition process.

3 DETECTION OF

OVERLAPPING ZONES

In this paper, we have proposed an approach for the

detection of intersection in surfaces. When a light

plane hit different surfaces, that is to say surfaces of

a same object with different orientations or depth

values, or hit surfaces of different objects, a

discontinuity effect is caused in the projection

planes. The discontinuity is caused by the breakage

Figure 1: A same perception for different occluded

objects.

VISAPP 2006 - IMAGE ANALYSIS

502

of light beam projection; thus several projection

planes displaced in the space can be observed.

Our active vision system consist of a light

pattern projector LASIRIS SNF, with a wavelength

of 660nm, a power of 20mW, a fan angle about 15º

and 7 concentric circles with an interbeam angle of

0.77º, and a CCD camera. The intrinsic and extrinsic

parameters of the camera are not necessary to know

them to the overlapping detection, because

reconstruction task are not made. Only, when the

camera is wanted to reposition, both the intrinsic and

extrinsic parameters of the camera are assumed from

the pre-calibration offline.

3.1 Approach of Contours

In our work, the first stage consists of extracting the

contours of circle pattern. To do it, firstly, a

Gaussian smoothed process with a 3x3 size mask is

done to reduce the produced noise when the beam

hit too reflecting surfaces. Later, the image is

binarized by means of a suitable threshold,

according to the wavelength of the laser.

Experimentally, a luminance threshold about 70 has

been considered for 660nm. With this threshold it is

possible to extract only the information of contours

from the projected laser pattern.. Next, the projected

circles in the image are detected by means of a

convolution process. In this process, 8-connectivity

masks are used (Teh, 1989). Thus, the pixels which

determine each contour are found. This set of pixels

corresponds to the 2D-points which compose each

projected circle are fit by a polygonal approach.

The advantages of a polygonal approach are, on

the one hand obtaining a simple representation for

each contour which permits a fast and efficient

comparison process between contours. On the other

hand, we have the advantage of the reduction of the

number of interest points detected during the contour

extraction process. Thus, the beam projection is

only represented by a minimum set of interest points

without loss of stability in the contour extraction

process (Figure 2).

Our approach method is based on the Douglas-

Peucker’s algorithm (Douglas, 1973)(Hersberger,

1993). Where, each contour is approximated by a

poly-line, P

. If a contour is defined as a sequence of

n points so that

{}

pppC ,...,,

= , a poly-line P

can be defined as the union of 1-degree segments,

where l denotes each segment.

{}{ }

10/)1(

≤≤−+==

−

tpttpllP

{}

2...

≥= nppP

The adjustment is based on the representation of

set of points by means of edge segments where the

proximity of each point to the edge segment must be

inferior to a tolerance factor

which is taken like

reference threshold. The proximity is measured like

a normal distance vector to each candidate edge

segment.

The algorithm begins approximating all the

points of a same contour,

{}

pppC ,...,,

= , with

a poly-line which joins the fist and the last point of

the edge contour,

{}

pplP

. The distance of

each intermediate point to the poly-line is measured,

and the farthest point with a tolerance greater than

the

value, is added to the simplification process

and takes part to build a new poly-line

{

}

nis

pppP

. Later, this one is divided into two

segments

{

}

ppl

and

{}

ppl =

and the union

of both will compose as

{}{ }

nis

pppllP

121

, == .

Thus, these steps are repeated iteratively for each

edge contour until all the points which belong to the

poly-line do not violate the value rank marked by the

tolerance factor. If the distance of an intermediate

point to a poly-line is inferior to the tolerance factor,

this one is not taken into account for the

simplification process of the poly-line. The

polygonal adjustment process has permit to

approximate the laser beam contours in a more

stable way than a set of contour points. Now, each

edge contour is composed by an inferior number of

points. Each contour is a set of points greater than

two which it is the minimum number of points

necessary to define a segment.

Nevertheless, in spite of the previous smoothing

pre-processing, during the contour detection process,

some contours have been approximated by poly-

lines of small length, this polylines are formed by a

Original

contours

Approach

contours

Figure 2: Approach of a beam.

A DETECTION METHOD OF INTERSECTIONS FOR DETERMINING OVERLAPPING USING ACTIVE VISION

503

small number of points. This fact can be due to

noise, contour points which contribute with little

information because it represents very small and

despicable discontinuities. Therefore, the

approximated contours should be filtered in order to

work only with those having some length and are

determined by a number of points greater than three

{}

3...

≥= npppP

. Once filtrated, it is

necessary number the candidate contours again with

a new numberation, despising those which are not

useful because they do not contribute with important

discontinuity information or because they can cause

confusion.

3.2 Clustering and approach of

discontinuity

Once, the polygonal approaches have been filtered,

the end points are only chosen. These points are the

tactically important points which will determine the

directions of discontinuity

{}

≥= nppP

. These

directions of discontinuity are not but the zones of

breakage of the light beam projections, when the

beam hit over two surfaces with different depth or

orientation. Later, a method of adjustment of the

tactically important points is applied by means of

straight lines. These straight lines determine the

candidate zones and the suitable direction for the

search of possible discontinuities which are present

in the changes of surface (Figure 3).

A clustering process of tactically important

points is carried out to be able to determine

whichever straight lines are necessary to fit them,

and to discrimante what tactically important points

belong to one or intersection. The clustering process

permits to group the tactically important points

according to two parameters: inertial moments

(Chavez, 1999) and metric distances (Teague, 1980).

Thus, each edge contour approximated by a poly-

line

P has two tactically important points, each one

must belong to different clusters, and must have

associated the central moments of the poly-line to

which they belong. The central moments are

invariant to transfering identical beams in the image,

and they do not depend on the position that the beam

projections have in the image.

∫∫

−−= dxdyyxfyyxx

cqp

),()()(

Furthermore, it is possible to determine the

rotation of each edge contour around its gravity

centre from the central moments and with the aid of

the components of inertial tensor, as:

2,00,2

1,1

arctan

μμ

−

The parameter of inertial moments is employed

to discern between tactically important points which

belong to poly-lines, and therefore to contours with

the same orientation. This way, we have supposed

that the beam projections over the same surface of

an object A have similar inertial moments. Although,

in an object B which is overlapping and occluding

part of surface of A, the inertial moments estimated

from the beam projections over a surface of B, are

different to those estimated from A (Figure 3). When

a discontinuity is detected an orientation change of

the beam projections takes places, and consequently

a new value of the inertial moments.

Also, another parameter to emphasize is the

distance of Minkowski L

. Thus, the distance of

each tactically important point to the rest of

tactically important points is calculated, trying to

minimize it.

The distance parameter is used to avoid to group

as points of a same discontinuity, those points which

can agree at inertial moment, but due to their little

proximity they may not belong to the same

candidate zone. For this reason, only the tactically

important points, near among them and whose poly-

lines have similar inertial moments, are clusterized.

Then, we obtain n sets of points of the following

type:

{

}

nisssp

0/...

where

{}

sss ...

are the points nearer

p ordered according to

proximity. Finally, the difference of moments for

each set of points is obtained as it was mentioned

above. From the distances and the difference of

jiL

ppd

⎟

⎠

⎞

⎜

⎝

⎛

−=

∑

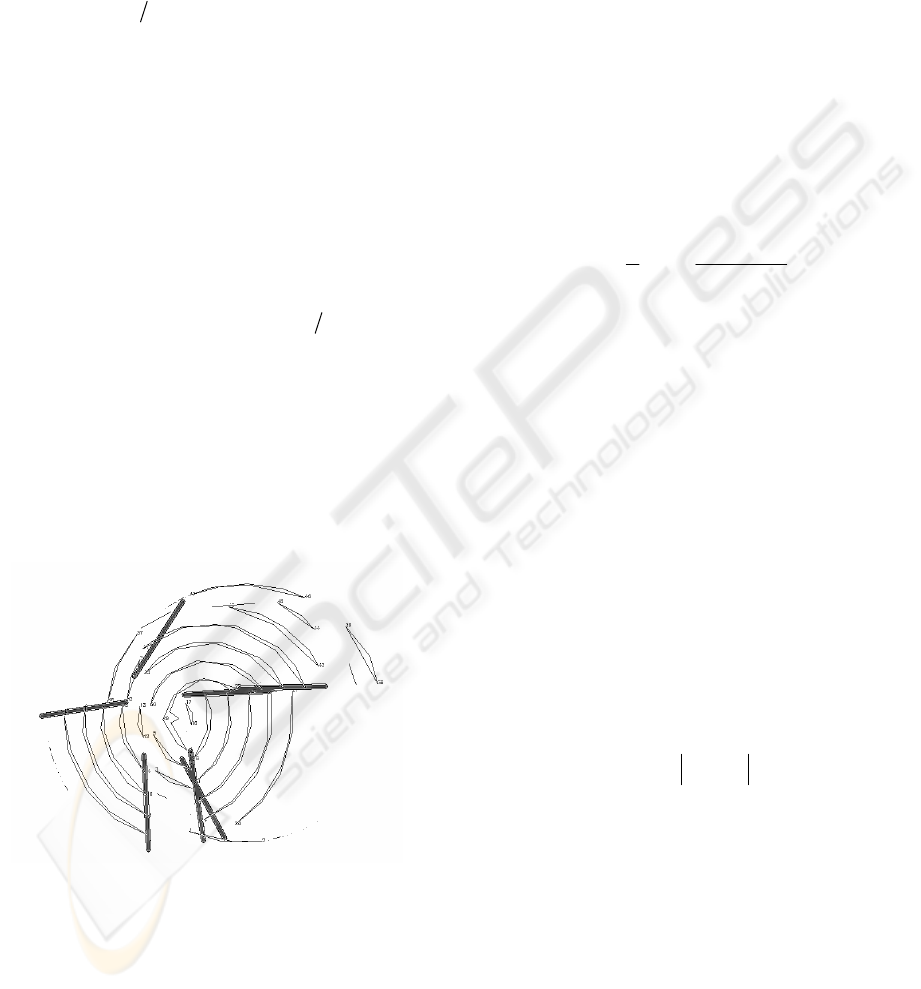
Figure 3: Intersection and discontinuity zones among

three objects.

VISAPP 2006 - IMAGE ANALYSIS

504

moments calculated for each set

{}

sssp ...

= ,

the clustering process is made. In this way, for any

two points

p and

, these will be able to be

jointly stored and included in the same cluster,

solely if they fulfill that

cij

< , with

the

angular tolerance allowed to consider it similar

orientation.

Finally, after the tactically important points have

been grouped by means of the clustering process,

(Figure 4), the candidate zones which represent

discontinuities in the image are defined as those

zones which cotain each cluster. In order to

determine the search direction of those candidate

zones and their boundary, it is necessary to make a

linear adjustment by least-squares method which

calculates the straight line segments which diminish

the Minkowski’s distance L

-L

of each set of

tactically importan points to the straight line

segment (Figure 3).

In Figure 4, the clustered sets of points are

represented by different colours.

The 2D-representation shows the relation of

distance among the points of each cluster.

Furthermore, in the distribution space of clusters

shown in Figure 5, it is observed that using jointly

parameters like distances and inertial moments,

points which could be considered very different can

be grouped. Thus, figure 5 shows the relation

between the pose of each point in image space and

its inertial moment.

The coloured points determine the intersection

zones between two objects. Thus, figures 4 and 5

represent the clusters used for the approach shown in

figure 3.

4 EXPERIMENTAL RESULTS

In our experiments, the objects used are

polyhedrons. We have not considered objects with

smooth surfaces. The size of captured image is

768x576 and all images have been acquired with a

monochrome CCD in our laboratory.

The experimental results exhibit satisfactory

coherence in the spatial detection by discontinuities

when the discontinuities are caused by overlapping

(Figures 6b and 6c). However, the proposed method

works correctly and it is valid when the

discontinuities are caused by contact between sides

of two very near objects (Figure 6a).

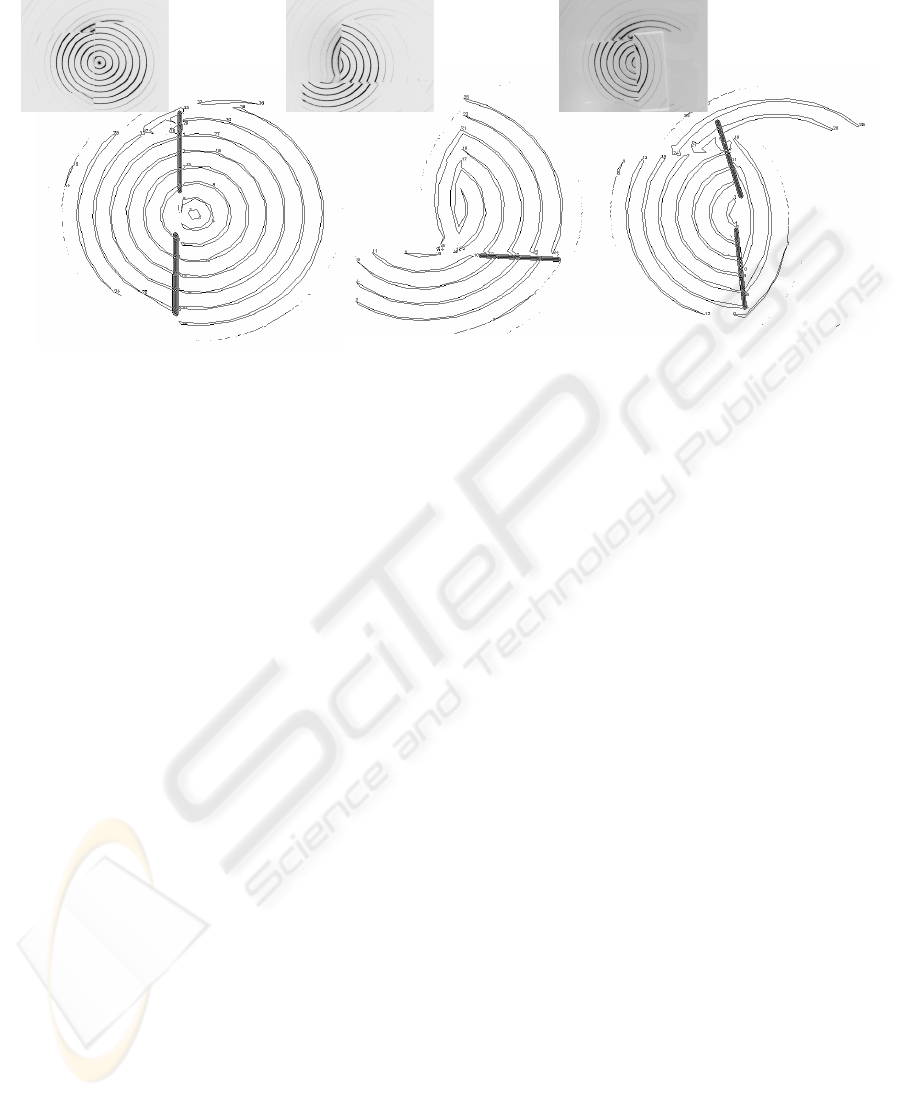
Figure 6 shows the application of the proposed

method on the detection of intersections among

objects. In our method, the intersections are well

detected while other type of discontinuities is not

detected because they are not caused by the

intersection between objects. In Figure 6a, two

objects have a side of contact and therefore a

discontinuity is caused by the contact between both.

In Figures 6b, and 6c, there is an overlapping

between both objects. This overlapping is caused

because an object called B is located upon another

one A. Moreover, there is an occlusion because B

hidden part of surface of A. In theses two cases, the

discontinuities caused by overlapping are only

detected.

sjpiij

θθθ

−=

200 300

400 500

600 700

Figure 4: 2D-Representation of the clustering process.

200

300

400

500

600

700

100

200

300

400

500

-60

-40

-20

Figure 5: 3D-Representation of the clustering process.

A DETECTION METHOD OF INTERSECTIONS FOR DETERMINING OVERLAPPING USING ACTIVE VISION

505

5 CONCLUSION

In this paper, we studied the occlusion by

overlapping using concentric pattern projections.

The developed method was implemented with

satisfactory experimental results. The system can

work well for detection of simple polyhedral

surfaces without requiring apparent features. In the

practice this system is used jointly with colour

segmentation techniques. This active vision system

is useful for occlusion detection when there are

several objects in the scene with a same colour. In

this case, the colour segmentation techniques fail. In

addition, it is also useful to provide additional

information when they work well, this is when the

objects have colour different. Perhaps, an analysis of

the proposed method could suggest that a method

based on range data analysis could be applied to

obtain discontinuities from depth information of a

more robust way. However the computation of depth

data requires a previous camera calibration, and

therefore a triangulation method to calculate the 3d-

space coordinates. The method proposed permits to

work with cameras with unknown intrinsic and

extrinsic parameters as opposed to the methods

based on range data. In many recognition

applications, in which the camera changes the

localization and focal length, the use of the proposed

method is an advantage because a recalibration of

laser-camera system is not a necessary.

REFERENCES

Bhanu B., Lin Y., 2003. Stochastic models for recognition

of occluded target. Pattern Recognition 36, pp. 2855-

2873.

Boshra M., Ismael M.A., 2000. Recognition of Occluded

Polyhedra from range images. Pattern Recognition

33, pp. 1351-1367.

Chan C.J., Chen S.Y., 2002. Recognizing Partially

Occluded Objects Using Markov Model. International

Journal of Pattern Recognition and Artificial

Intelligence 16(2), pp. 161-191.

Chavez, E., Navarro G., Baeza-Yates R., Marroquín J.,

1999. Searching in metric spaces.

Technical Report TR/DCC-99-3, Dept. of Computer

Science, Univ. of Chile.

Douglas D., Peucker T., 1973. Algorithms for the

reduction of the number points required to represent a

digitized line or its caricature. The Canadian

Cartographer 10(2), pp. 112-122.

Hershberger J., Snoeyink J., 1993. Speeding Up the

Douglas-Peucker Line-Simplification Algorithm.

Proc. 5

Symp. On Data Handling, pp. 134-143.

Teague M.R., 1980. Image Análisis via the general theory

of moments. Journal of Optical Society of America

70(8), pp. 920-930.

Teh C.H., Chin R.T., 1989. On the detection of dominant

points on digital curves. IEEE Trans. PAMI 1(8), pp.

859-872.

Park B.G., Lee K.M., Lee S.U., Lee, J.H., 2003.

Recognition of partially occluded objects using

probabilistic ARG (attributed relational graph)-based

matching. Computer Vision and Image

Undesrstanding 90, pp. 217-241.

Figure 6: Results for different pose of o

jects (real objects in part superior and image

processed in part inferior).

A B A

)

VISAPP 2006 - IMAGE ANALYSIS

506

Ulrich M., Steger C., 2001. Empirical Performance

Evaluation of Object Recognition Methods. Empirical

Evaluation Methods in Computer Vision. IEEE

Computer Society Press. Los Alamitos, C.A., pp. 62-

76.

Ying Z., Castañon D., 2002. Partially Occluded Object

Recognition Using Statistical Models. International

Journal of Computer Vision 49(1), pp. 57-58.

A DETECTION METHOD OF INTERSECTIONS FOR DETERMINING OVERLAPPING USING ACTIVE VISION

507