COMPUTER VISION BASED INTERFACES FOR INTERACTIVE

SIMULATIONS

Ben Ward, Anthony Dick

School of Computer Science, University of Adelaide, Adelaide, SA 5005, Australia

Keywords: Real-time Vision, 3D Motion and Tracking, Human-Computer Interaction.

Abstract: 3D environments are commonplace in applications for simulation, gaming and design. However, interaction

with these environments has traditionally been limited by the use of 2D interface devices. This paper

explores the use of computer vision to capture the 3D motion of a handheld object by tracking known

features. Captured motion is translated into control of an object onscreen, allowing 3D interaction with a

rendered environment. Objects are tracked in real-time in video from a single webcam. The technique is

demonstrated using two real-time interactive applications.

1 INTRODUCTION

With the growing power of personal computers, 3D

environments have become a common feature of

applications for gaming, simulation, art, and design.

However, these 3D applications often require

complex combinations of keys, mouse buttons and

mouse motion to map 2D input to 3D motion. The

interface described in this paper bypasses traditional

controls, enabling 3D motion to be captured visually

and used to directly drive interaction in 3D

environments.

This system was designed for use as a general-

purpose 3D interface in a home or office

environment. As such, it would have to meet a

number of challenging requirements:

– No use of expensive specialized hardware

– Run in real time on a current desktop PC

– Track in 3D with sufficient accuracy for

intuitive control

– Cope with fast motion

– Cope with variation in lighting conditions

– Cope with background clutter

To our knowledge, no existing system (including

this one) fulfils all of these criteria. However, we

adopt and adapt several techniques from computer

vision and graphics to address these issues in a novel

way.

Significant effort has also been invested in

developing convincing demonstrations of how these

interfaces can be applied to games and other

applications involving physical simulation, where

the interface enables direct interaction between real

and simulated objects. The interfaces are general-

purpose enough that they could be adapted to other

applications, such as the manipulation of objects for

3D design and visualisation.

An overview of the system is as follows. Colour-

based tracking is used to locate and follow the 2D

motion of a simple handheld object by identifying

one or more features, as described in section 2. That

motion is then refined and transformed into 3D

motion based on knowledge of the camera and the

object, as described in sections 3 and 4. Five degree

of freedom motion is enabled by tracking a pair of

features. The recovered 3D motion is used to interact

with a rendered environment, as described in

sections 5 and 6.

1.1 Related work

The field of computer vision has produced a range of

new and inventive user interfaces. However, few

meet the requirements of a general-purpose 3D

interface.

Vision-based interfaces typically track some

movement of the body, such as hand gestures (Yang

and Ahuja, 1999), or eye gaze direction (Kim and

Ramakrishna, 1999). Much of the work in this field

has focused on 2D interfaces (eg. Chung et al., 2002;

Sony Eyetoy). Systems for tracking motion in three

dimensions are more difficult to implement, as they

must recover the depth information lost in

translating a 3D scene into a 2D image. Robust 3D

389

Ward B. and Dick A. (2006).

COMPUTER VISION BASED INTERFACES FOR INTERACTIVE SIMULATIONS.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 389-394

DOI: 10.5220/0001366403890394

 SciTePress

vision interfaces developed so far require the use of

multiple cameras (Hartley and Zisserman, 2000) or

detailed knowledge of the tracking target. In

addition to vision-based interfaces, systems exist for

robust 3D interfaces based on other technologies

(eg. Immersion Corporation). However these require

specialized hardware and are rather expensive.

2 COLOURED OBJECT

IDENTIFICATION

Object colour provides a relatively simple and fast

means of identifying object features, and is widely

used in tracking applications, such as the 2D game

interfaces in Chung et al. (2002). It is also robust to

video artefacts such as motion blur and shape

distortion, which can appear when the target is

moving quickly.

To reduce the variation in object colour due to

lighting, data for each frame is transformed from the

RGB colour space to the HSV colour space (Smith,

1978), to separate colour hue and saturation values

from brightness. To identify pixels belonging to the

tracked object, thresholding is performed on each

frame, testing each pixel against predetermined hue

and saturation values for the tracked features. These

values are acquired during the initialization of the

interface, by holding the object to be tracked in an

area indicated by an onscreen icon.

Morphological filtering operations (Haralick et

al., 1978) are applied to improve raw thresholding

results. With the threshold set high enough for most

pixels of the tracked features to pass, a significant

number of scattered background pixels also tend to

survive. Erosion and dilation operations are applied

to remove background noise, and reduce the size of

missing areas of the tracked features.

Filtered points are grouped with a connected

components algorithm (Rosenfeld and Pfaltz, 1966)

to determine which belong to the tracked object, and

which belong to the background. Figure 1 shows an

example of threshold results and point grouping.

Figure 1: Threshold and grouping results.

2.1 Real-time colour tracking

Performing the HSV transformation on a complete

frame of original video is expensive, and

unnecessary, as high resolution information is only

required for making a precise determination of

properties of the tracked features. To increase

efficiency, while still locating the tracked object

even under rapid movement, HSV transformation is

performed at two scales.

Transformation and filtering operations are first

performed on a low-resolution version of the frame,

generated by standard graphics hardware. Areas of

the image likely to contain the tracked features are

identified using HSV thresholding. Transformation,

filtering, and grouping are then performed on those

areas of the original, high-resolution frame.

3 SINGLE FEATURE TRACKING

A single feature point with known size and shape

properties was tracked in the initial stage of the

project. By tracking the position of the feature, a

user interface can be constructed where object

motion controls a 2D position. From the size of the

feature in each frame, and the parameters of the

camera, the feature position in 3D space can be

estimated. A coloured ball was selected to provide

this initial feature, due to its sufficiently simple

shape properties. However, other shapes could be

used, provided the centre and bounding sphere could

be reliably estimated.

3.1 2D Feature Tracking

From the chosen pixel group, initial estimates for the

centre and radius of the circular feature are

determined by applying a smallest enclosing disk

algorithm (Nielsen and Nock, 2004) to points around

the edge of the group. The result of this algorithm is

the centre and radius of a circle containing the

complete set of edge points. Estimates are

reasonable, even when substantial sections of the

feature are occluded or lost in thresholding.

However, as this circle encloses all points, single

outlying points can significantly alter the centre and

radius of the disk.

These estimates can be improved by determining

the mean and standard deviation for the distance

between edge points and the initial centre, and

rejecting outliers. Estimates can be further improved

by averaging over a randomised set of centre

estimates, obtained by selecting sets of 3 edge

points, and calculating the centre from the

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

390

intersection between the normals of lines connecting

the points along the arc of the circle. Final estimates

are shown in Figure 2, including estimates in the

presence of occlusion.

Figure 2: Centre point and enclosing disk.

3.2 3D Feature Tracking

The 2D position and radius estimates for the tracked

feature are used to determine a position in 3D space.

The relationship between a scene and the image

plane of a camera can be modelled through

perspective projection, with a point in space

appearing in the frame at the intersection of the

image plane and a ray between the point and the

camera’s optical centre. As the object is far from the

image plane relative to its own size, the geometry of

the projection can be simplified with a weak

perspective assumption, where all points on the

object are assumed to be approximately the same

distance from the camera (Alter, 1992) The ray

between the camera and the centre of the object is

assumed to be perpendicular to the image plane, as

shown in Figure 3. If the focal length of the camera

and the size of the tracked feature are known,

position in space can be determined from position

and radius in the image.

Figure 3: Weak perspective projection.

The Z position of the feature is determined from

the focal length of the camera f, radius in the frame

r, and radius of the ball R by

fR r=

. Having

estimated the distance of the feature from the camera

Z, perspective projection is used to determine the 3D

position of the feature. X and Y coordinates for the

tracked feature, as shown in Figure 4, are

determined from f, Z, and the vector (x,y) from the

centre of the frame to the centre of the feature in the

frame by

(,) (,)/XY Zxy f

Figure 4: Determining X and Y position.

4 FEATURE PAIR TRACKING

Tracking the movement of a single feature point in

3D is sufficient to create simple 3D user interfaces.

However, control in such an interface is limited to

three degrees of freedom. For more complex control

and interaction, an interface should provide control

over both 3D position and orientation.

To allow for greater degrees of control, a pair of

features were tracked in the next stage of the project

to define a 3D vector, providing a 3D position, and

rotation about two axes. Two easily identified

features were provided by same-coloured markers

on a cylindrical wand. In estimation, the markers are

approximated as rectangular sections of the tracked

wand, with a major and minor axis.

4.1 2D Feature Pair Tracking

Tracking the feature pair requires correctly

determining which group of points corresponds to

which marker in each frame of video. From the

initial set of pixel groups determined by connected

components, any group with number of pixels below

a minimum is rejected. Groups are also rejected if

their distance from either feature in the previous

frame, or the ratio of their size to the size of either

feature, is too great. Thresholds are loose, to discard

only unambiguous outliers. From the remaining

pixel groups, groups corresponding to tracked

features are selected by proximity to features in the

previous frame.

An initial estimate for the centre of each feature

is determined from the smallest enclosing disk

algorithm. Estimates of feature width and length are

obtained by linear searches for edge points along the

line connecting the features in the image and its

normal. Each search begins at a point shifted some

COMPUTER VISION BASED INTERFACES FOR INTERACTIVE SIMULATIONS

391

number of pixels from the estimated centre of a

feature along the perpendicular to the current search

line. Results are averaged over multiple searches.

Figure 5: Estimated length and width along connecting

line and its normal.

From the estimated length and width, midpoints

are found for lines across the length and width of the

feature, defined by the relative position of the

features’ centres. These midpoints lie on lines

bisecting the feature, as seen in Figure 5. The

intersection of two lines, centred on the midpoints,

in the direction of the connecting line and its normal,

provides a better estimate of the centroid of the

feature, as shown in Figure 6.

Figure 6: New centroid estimate (hollow circle).

From the improved estimates of the centre of

each feature, the estimate of the connecting line can

also be improved. Iterating this process several times

provides reliable approximations of each feature’s

centre, length, and width.

4.2 3D Feature Pair Tracking

Initial attempts at estimating 3D position and

rotation used feature width to determine Z positions.

However, this proved to be problematic under some

lighting conditions. For a cylinder, shade tends to

vary across its width. Feature width may be incorrect

if one side of the cylinder is in shadow, or if bright

reflections along the length of a feature divide it into

multiple sets of points. These issues can be avoided

by ignoring width, instead using feature length and

the distance between the feature centroids in the

frame. Z position can be determined from this

distance, provided rotation of the wand around the x-

axis is known. Again assuming weak perspective,

the scene can be approximated as seen in Figure 7.

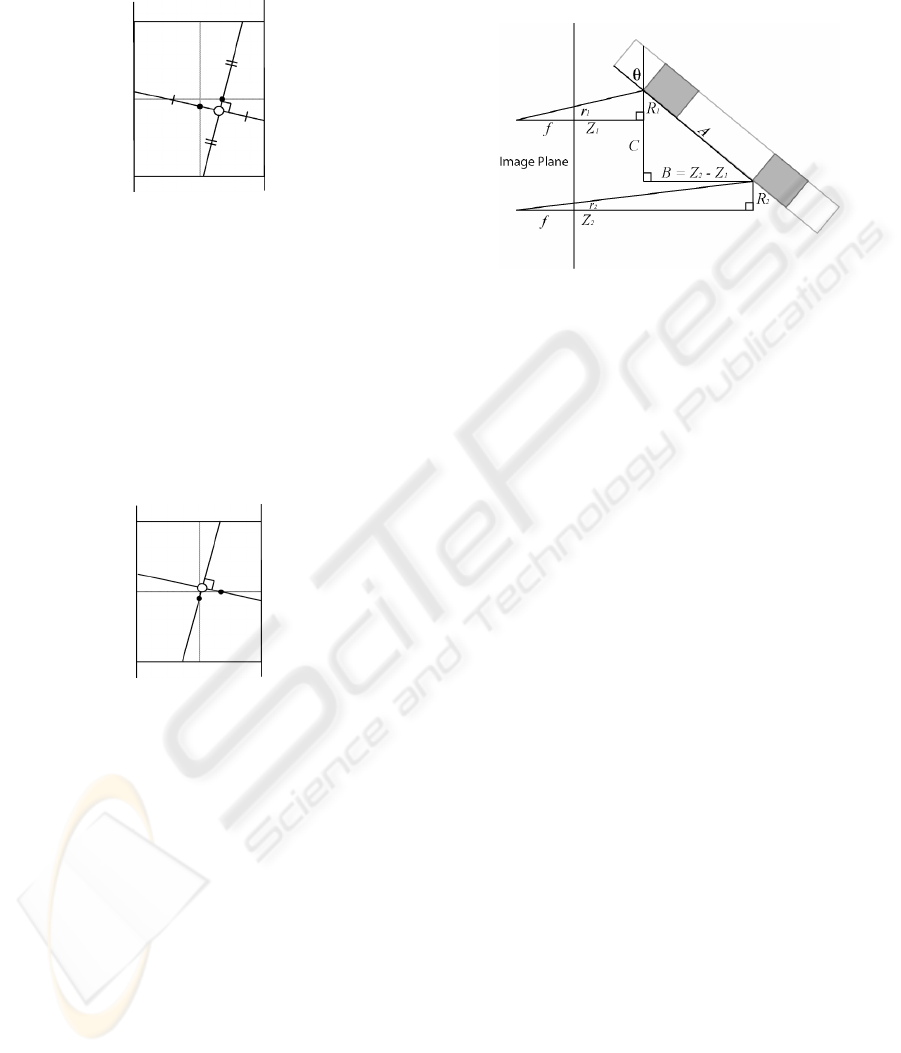
Figure 7: Weak perspective projection.

/ii i

rZ R

, and

12RR=

for features of

equal length,

11 2 2rZ rZ=

, and

21 112()(/1)ZZ Zrr

−

=−

. The distance

21BZ Z=−

from which θ can be determined, can therefore be

estimated from one Z position, and the relative

lengths of the two features in the frame,

and

are known, Z position and rotation

around the x-axis can be estimated by finding a Z

position for one feature for which the distance

between the features of the rotated wand, projected

onto the image plane, matches the distance between

the centroids of the features in the frame. The

problem of estimating position and rotation therefore

resolves to a 1D search for a single Z value.

This Z value is determined with a binary search

over the range of distances for which the features

can be reliably tracked. Z position is initialised to the

midpoint of this range. For

11 2(/ 1)BZrr=−

, x-axis

rotation θ is given by

sin( / )BA

. Distance

between the features along the y-axis C is given by

/tan( )CB

. This distance is projected onto the

image plane, assuming Z position of the midpoint

between the features, as

1/( / 2)cfCZB

. If this

distance is less than the distance between the centres

of the features in the frame, the upper limit of the

search is set to the Z

estimate. Otherwise, it

becomes the lower limit. Through multiple iterations

of this search, reliable estimates are obtained for Z

position and x-axis rotation.

From this Z position, X and Y position can be

estimated by projection through the midpoint

between the feature centroids in the frame, giving all

values for a centre point C. The remaining unknown

is z-axis rotation, initially estimated by the angle α

between a vector connecting the centroids in the

frame and the y-axis. For vector Vc from the centre

of the camera to the centre of the tracked object, and

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

392

distance between a feature and the centre of the

object A, vector V

from the camera centre to a

feature, when the object is rotated by θ around the x-

axis and by the estimate α around the z-axis, is

given by

V =

(

.sin()*,

Vx A

. cos( )* cos( )* ,

Vy A

.cos()*sin()*

Vz A

)

The endpoint of the rotated object is projected

onto the image plane, as shown in Figure 8.

Figure 8: Projection onto the image plane.

intersects the image plane at point e:

The angle β between the line connecting e and c

and the y-axis is given by

asin(( . . ) / )ex cx e c

=−−

The difference between this value and the initial

estimate is removed from that estimate to give a

final value for z-axis rotation, φ:

αβ

=−

The set of values now obtained describe a point

in 3D space and rotations around two axes.

5 INTEGRATING REAL AND

SIMULATED OBJECTS

By determining the location and orientation of an

object in 3D space, motion of the tracked object can

control the motion of a rendered object. A 3D object

(in this case a cylinder) can also be mapped to the

position of the wand in video. Other 3D objects can

be introduced into the scene, and intersect the space

occupied by the cylinder. By redrawing the original

video source over visible areas of the cylinder, the

real and rendered objects appear to occupy the same

3D space. This integration is improved by adding

shadow effects, as seen in Figure 9. Collision

detection and physics simulation enable physical

interaction between the objects.

Figure 9: Integrating in video.

6 DEMONSTRATION

APPLICATIONS

A simple table tennis game, seen in Figure 10, was

developed to demonstrate the ball-tracking interface.

The motion of the ball controls 3D movement of the

user’s paddle. Velocity determines the power of a

shot. This demonstration shows that the 3D ball

interface can provide precise control in real time.

Figure 10: Table Tennis demo.

In the mini golf demo, seen in Figure 11, a basic

golf game is played entirely through the tracked

wand. A rendered golf course is shown in front of

the player. The wand can be used to rotate and view

the course. When the player is ready to make a shot,

holding the wand close to the golf ball triggers a

perspective change to behind the ball, where the

tracked wand controls a rendered golf club.

This application demonstrates the versatility of

the wand interface. The wand is used for selection,

for 3D manipulation of the course, and for physical

interaction between the golf club and the ball.

COMPUTER VISION BASED INTERFACES FOR INTERACTIVE SIMULATIONS

393

Figure 11: Mini Golf demo.

6.1 Performance

The interface was designed to be sufficiently

accurate to provide intuitive control and create a

convincing visual integration between real and

rendered objects. The accuracy of wand motion and

rotation has been tested in favourable lighting

conditions. Measurements were made at a range of

distances from the camera, with observations

repeated multiple times and compared to ground

truth data. Results, seen in Table 1, predictably show

uncertainty of the position estimates increasing with

distance from the camera. Linear movement

estimates are reasonably accurate, compensating

well for the effect of perspective on motion parallel

and perpendicular to the camera. However, a

substantial degree of inaccuracy is seen in x-axis

rotation estimates at a significant distance from the

camera.

Far (75cm) Mid (55cm) Near

(40cm)

10cm X

Translatio

10.03±0.09 10.02±0.06 10.03±0.0

10cm Z

Translatio

9.98±0.59 8.37±0.20 9.91±0.09

45° Z

Rotation

44.96±0.32 44.94±0.23 45.68±0.2

45° X

Rotation

45.28±4.61 39.76±2.76 45.39±1.0

In less favourable conditions, the presence of

bright light sources, shadows on the tracked features,

or noise due to low light can degrade performance.

However, a sufficient degree of control can be

achieved in most realistic indoor situations in which

the system was tested. As the tracking system is

based on colour, tracking problems are most

noticeable in situations where the colour of the

tracked features is present in substantial areas of the

background or user.

7 CONCLUSION

This paper has described methods of tracking a

known object in 3D in a single camera, through

properties of recognized features. This tracking is

used to create genuine 3D user interfaces that can be

used for direct interaction with 3D environments

integrating real and simulated objects. These

interfaces are suitable for use in a home

environment, with current computing hardware.

The current system is limited in terms of the

range of objects that can be tracked, requiring

markers to provide identifiable features for tracking

that incorporates rotation. However, the scope of the

fundamental system is broad enough that it could be

substantially extended with future development, and

further demonstrate the implementation and use of

original forms of human-computer interaction.

REFERENCES

Alter, T. D., 1992. 3D Pose from 3 Corresponding points

under weak-Perspective Projection. Technical Report

1378, MIT Artificial Intelligence Laboratory.

Chung, J., Kim, N., Kim, G.J., & Park, C.M., 2002. Real

Time Motion Tracking System For Interactive

Entertainment Applications. Proceedings of the 5th

International Conference on System Simulation and

Scientific Computing.

Haralick, R.M., Sternberg, S.R., & Zhuang, X., 1987.

Image analysis using mathematical morphology. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. 9, No. 4, pp. 532-550.

Hartley, R., Zisserman, A., 2000. Multiple View

Geometry In Computer Vision, Cambridge University

Press.

Immersion Corporation, http://www.immersion.com

Kim, K., Ramakrishna, R.S., 1999. Vision-Based Eye-

Gaze Tracking for Human Computer Interface.

Proceedings of the IEEE SMC’99 Conference, No.2,

pp. 324-329.

Nielsen, F., Nock, R., 2004. Approximating smallest

enclosing disks. Proceedings of the 16th Canadian

Conference on Computational Geometry, pp. 124-127.

Rosenfeld, A., Pfaltz, J.L., October 1966. Sequential

operations in digital picture processing. Journal of the

ACM, Vol. 13, No. 4, pp. 471-494.

Smith, A.R., 1978. Color Gamut Transform Pairs.

Proceedings of SIGGRAPH 78, pp. 12-19.

Sony EyeToy, http://eyetoy.com

Yang, M-H., Ahuja, N., 1999. Recognizing hand gesture

using motion trajectories. Proceedings of the IEEE CS

Conference on Computer Vision and Pattern

Recognition, pp. 468-472.

Table 1: Mean values and standard deviation for estimates

of movement in 3D space.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

394