AN IMAGE REGISTRATION TECHNIQUE FOR DETECTION OF

CRACK AND RUST GROWTH

Norihiko Itoh

Central Research Institute of Electric Power Industry

2-11-1 Iwado Kita, Komae-shi, Tokyo, Japan

Keywords:

Computer vision, Image processing, Pattern recognition, Fourier transform.

Abstract:

To observe and record the progress of cracks and rusting, it is necessary to compare the images of the past

with those of the present. The angles of surfaces of structures such as a concrete wall taken vary according to

the camera position, that is the location in which they were taken. The images that were taken from different

points are distorted, deformed or appear as if the actual location of the cracker rust has been shifted. So

need less to say, the uses of these images are not good means of accurately detecting the progress of crack

and rusting. It is ﬁrst necessary to make rectiﬁcations. This can be done by using the images as a basis in

determining the correct camera location and the adjustments made thereof. This paper proposes the difference

of the camera angle can be detected by applying the frequency element of the whole image. Especially, this

method is effective for a surface with few features such as a concrete wall.

1 INTRODUCTION

Recently with the availability on high quality digi-

tal cameras, it is now easier to record and store the

progress of the cracks on the dam-gate or concrete

area. The observation period is lengthy due to the

slow progress of the cracks or rust and it is common

to record and compare the cracks or rust on a regular

or irregular basis.

The angles of surfaces of structures such as a con-

crete wall taken vary according to the camera posi-

tion, that is the location in which they were taken.

The images that were taken from different points are

distorted, deformed or appear as if the actual loca-

tion of the cracker rust has been shifted. Therefore,

the uses of these images are not good means of ac-

curately detecting the progress of crack and rusting.

Then, presumption and compensation of inclination

of those images are important. In order to grasp pro-

gresses of a crack or rust by the difference of images,

it is necessary to utilize a highly registration technique

sub-pixel or less.

Surfaces of structures such as dam-gate or other

huge facilities have few features. Due to the surface

simplicity it is difﬁcult to compare images using fea-

ture points. It is common to use mark point to pre-

sume the camera angle. However, in the case of huge

structures such as dam-gates, it is extremely difﬁcult

to set up indicators on the surface.

Many methods of presuming the camera angle from

images are proposed. Most of them (e.g. Ribeiro

(Ribeiro, 2000)) assume homogenous or isotopic tex-

tures.

Hwang (Hwang, 1998) proposed the method based

on wavelet transform to describe more complex tex-

tures. It focuses the energy concentration at some fre-

quency bands found by wavelet transformation. In ad-

dition, it is necessary to detect a peak of frequency

spectrum stably by this method. However, such con-

centration does not necessarily appear in textures like

the surface of concretes.

This paper proposes a high precision texture-based

image registration method. This method is based

on the spectrum and applicable to non-homogenous

and non-isotopic texture as well as Hwang’s, but this

method use phase-only-correlation, which uses only

the phase of spectrum representing the rich shape in-

formation. That is, the intensity of frequency spec-

trum is not used but carries out high registration of

accuracy only using the phase.

389

Itoh N. (2006).

AN IMAGE REGISTRATION TECHNIQUE FOR DETECTION OF CRACK AND RUST GROWTH.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 389-392

DOI: 10.5220/0001367303890392

 SciTePress

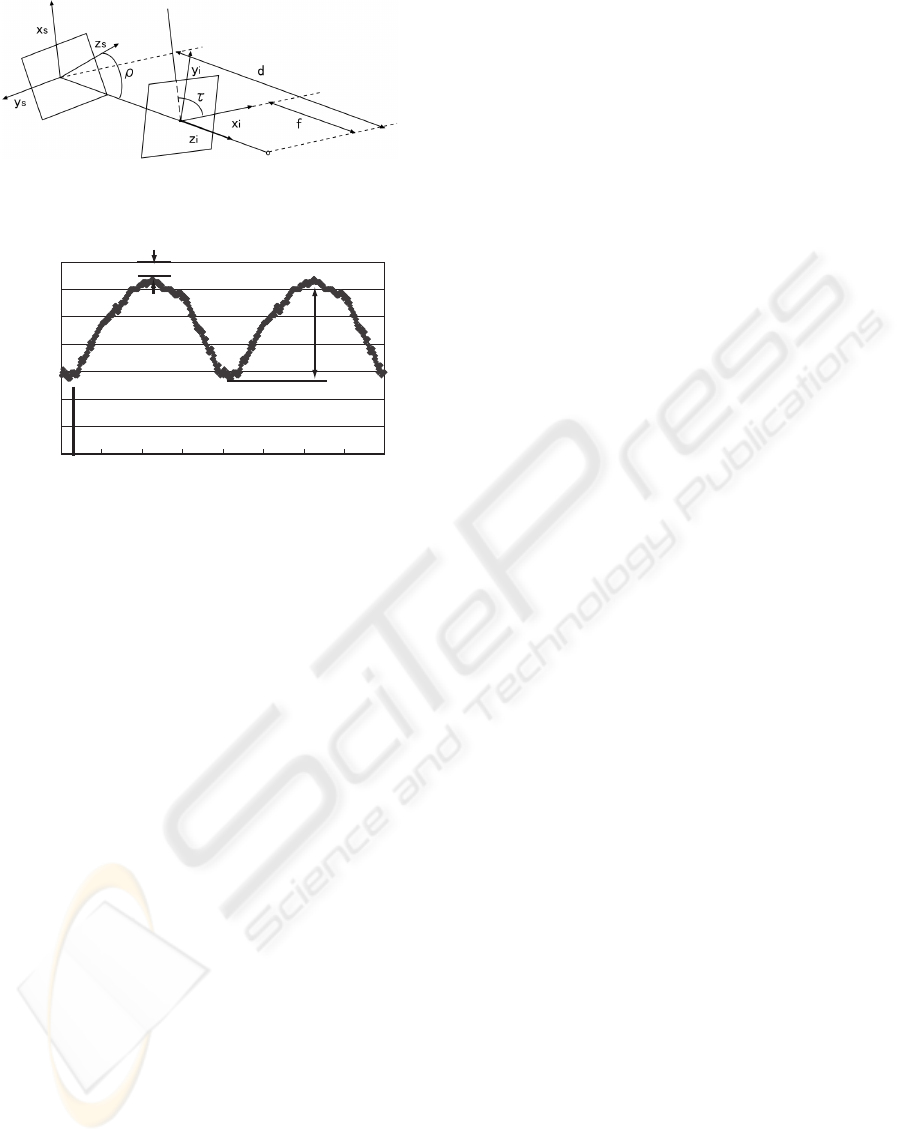
Figure 1: Location of camera and textured plane.

㪇㪅㪐㪐㪊

㪇㪅㪐㪐㪋

㪇㪅㪐㪐㪌

㪇㪅㪐㪐㪍

㪇㪅㪐㪐㪎

㪇㪅㪐㪐㪏

㪇㪅㪐㪐㪐

㪈

        

'PNCTIGOGPVTCVG

/GCUWTGOGPVFKTGEVKQP

UECNKPITCVG

EQUǹ

Figure 2: Scaling rate and slant-tilt angle.

2 PROPOSED METHOD

A camera projects the three-dimensional space onto a

two dimensional image. The projected image is de-

termined by 4 parameters, the distance d and the slant

ρ and the tilt τ and the rotation θ. Let the coordinate

systems of the object’s surface plane (x

) and

of the camera’s image plane (x

) and the focal

length f as depicted in Figure 1.

The slant angle ρ is deﬁned as an angle between

and z

, which takes nonnegative values between 0

and 90 (deg.). Furthermore, the angle between the

axis and the projection of the surface normal (z

onto the image plane (x

) is deﬁned as the tilt an-

gle τ, which takes values between −180(deg.) and

180(deg.). The slant-tilt combination represents the

orientation of a planar surface. An angle between the

axis and the projection of the x

axis is deﬁned as

a rotation angle θ.

The scaling, slanting, tilting, rotation of an image

all changes the power spectrum (amplitude of the spa-

tial frequencies) of the image but their effects are

different. For example, the rotation causes the rota-

tion of the spectrum and the scaling (zooming) causes

the isotopic scaling and the slant and the tilt cause

anisotropic scaling. Proposed method estimates all

the positional parameters including the scaling, the

slant and the tilt by comparing the spectrum of two

images.

The outline of the procedure is as follows:

1. Cancellation of the shift.

The proposed method ﬁrst calculates the power

spectrum of two images. This cancels the shift

(translation) between images because the power

spectrum of an image doesn’t change by translation

of the image.

2. Estimation of a rotation angle

Make the log-polar mappings of the two spectrums.

By this mapping, the rotation angle θ and a scale

factor λ is transformed to the translational displace-

ments between two images. After log-polar map-

ping, the proposed method calculates the rotation

angle θ of the images using phase-only correla-

tion (Takita, 2003). The rotation angle is computed

by the difference of peak coordinates in the θ-axis.

3. The calculation of an enlargement and reduc-

tion by the difference in a measurement direc-

tion.

The proposed method calculates the rate of

anisotropic scaling between the two log-polar spec-

trums. After log-polar mapping, this method de-

cides the direction of search. Two-dimensional

phase-only correlation is used for calculation of the

rate of enlargement. The rate of enlargement is

computed from the peak coordinates of the direc-

tion of λ. The rate of enlargement is calculated re-

peatedly by changing the direction to search. Con-

sequently, the enlargement for every direction is es-

timated.

4. The calculation of a rate of scaling, and the

slant-tilt angle ρ, τ .

The rate of enlargement and reduction of each mea-

surement direction changes in a shape of an ellipse.

A rate of scaling is calculated from the value of a

direction of a long axis, the inclination direction

of optic axis (τ ) is calculated from a direction of

a short axis, and the inclines angle ρ is calculated

from a ratio of a long axis and a short axis. The

relation between rate of the enlargement and the

slant-tilt angle ρ, τ is shown in Figure 2.

5. The calculation of the amount of movements of

the x, y direction.

First, an input image is rectiﬁed using inclination

direction of optic axis (τ ), and inclines angle ρ.

Next, the proposed method calculates the rotation

angle θ of the images using phase-only correlation

afresh. The input image is rectiﬁed using τ, ρ, θ.

Finally, using the reference image and the compen-

sated input image, the proposed method calculate

an amount of movements of x and y directions, and

image registration is completed.

A ﬂow of the proposed algorithm is shown in Figure

VISAPP 2006 - IMAGE ANALYSIS

390

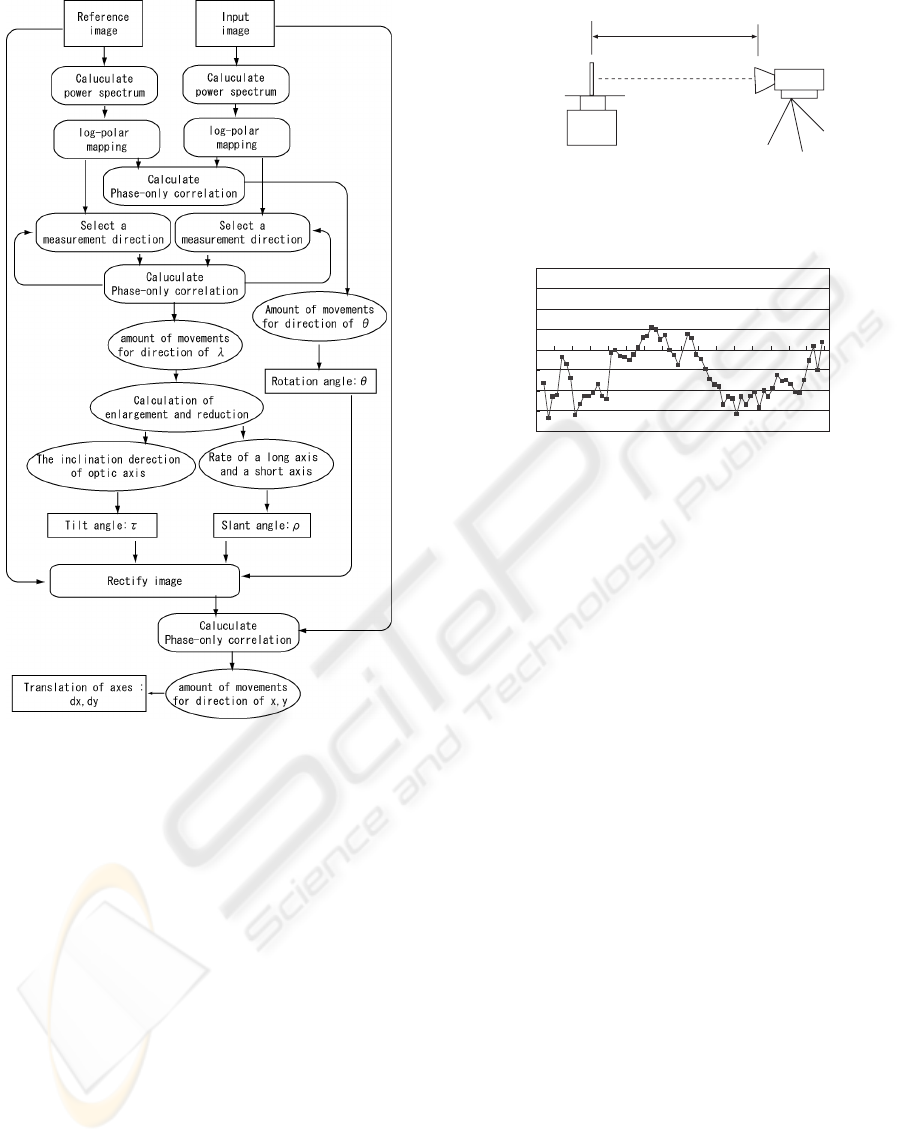
Figure 3: Outline of proposed algorithm.

3 PERFORMANCES

The images of cracks in concrete and rust in steel

taken at the time of inspections are usually non-

homogeneous and non-isotopic. So, two experi-

ments were performed. In the ﬁrst experiment, us-

ing the images of corkboard, which are typical non-

homogeneous and non-isotopic images, the camera

positions are controlled accurately. In the second ex-

periment, the camera positions are estimated, using

the images of the surface of a concrete wall taken by

a camera only ﬁxed by hands in a similar way at the

time of usual inspections.

3.1 Corkboard Surface

The proposed method is applied to the images of cork-

board taken by a digital camera (Nikon COOLPIX

950). The experimental environment is depicted in

Figure 4.

-4

3/6

9.5

Figure 4: Photography environment.

Slant angle(deg.)

Error(deg.)

-4

-3

-2

-1

-16 -12 -8 -4 0 4 8 12 16

Figure 5: An example of error vs slant.

The target corkboard is set on a rotation stand and

its distance from the camera is 1.2 meters. The center

of corkboard and the center of the camera’s lens are

at the same height. The stand is rotated from -15.5

degrees to 15.5 degrees by 0.5 degrees, which corre-

spond to the slants of surface orientation. The size of

images is 512 × 512 pixels. The image when the slant

is set to 0 is the reference image and the slant of the

rest images are estimated.

The estimation errors are shown in Figure 5. The

mean of absolute error was 1.44 degrees and the max-

imum error was 3.36 degrees. The error of 3.36 de-

gree corresponds to 0.44 pixels because 512/2 × (1 −

cos(3.36 deg.)) = 0.44.

When realizing equivalent accuracy using feature

points, it is necessary to detect all the feature points

with a less than 0.44-pixel error.

If it is an error of this level, an error is very small.

Therefore, the validity of the proposed method has

been checked.

3.2 Concrete Surface

The method is applied to the images of a concrete sur-

face of a wall taken by the digital camera next. In

usual inspections of dam-gates, tripods do not always

ﬁx the cameras. So, in this experiment, the camera

was ﬁxed by hand as well, not using a tripod. The

size of images is 256 × 256 pixels. The reference im-

age is shown in Figure 6 and the input image is in

Figure 7. The estimations by the method are that the

AN IMAGE REGISTRATION TECHNIQUE FOR DETECTION OF CRACK AND RUST GROWTH

391

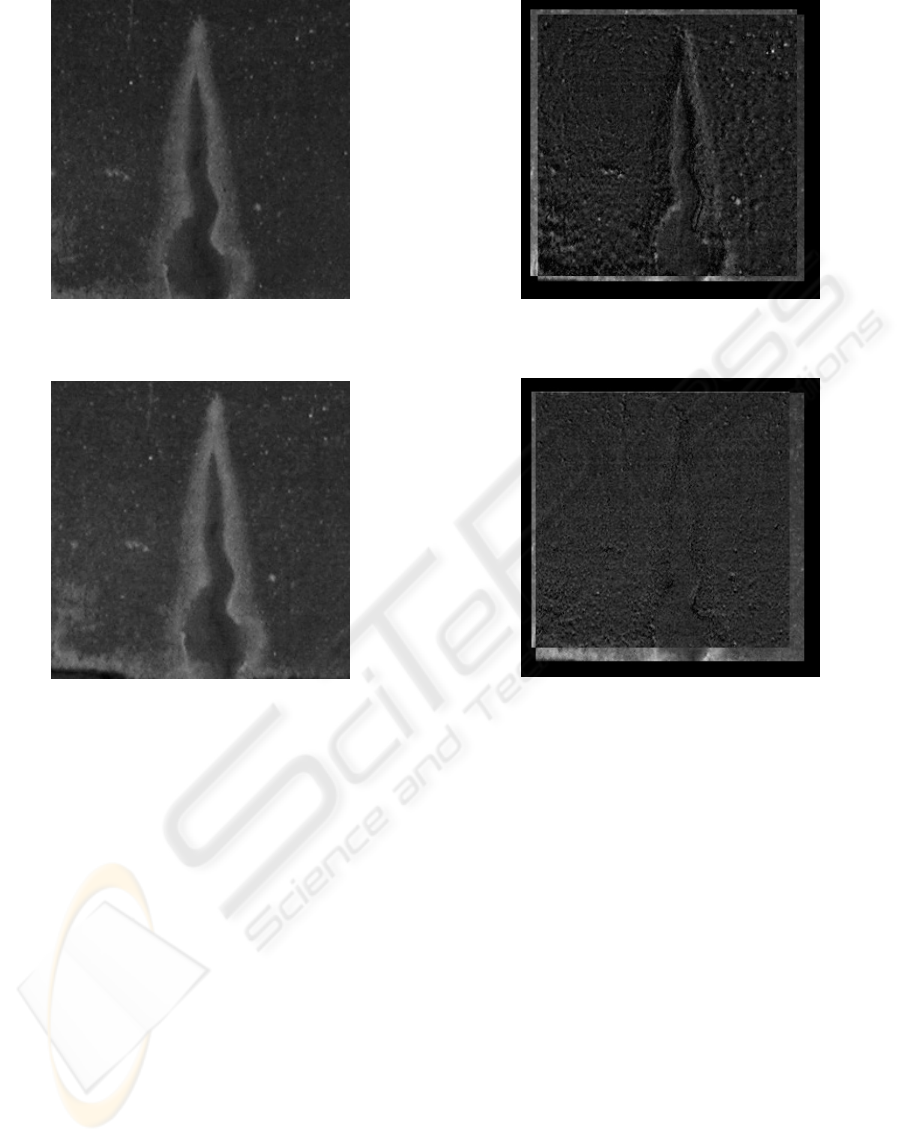
Figure 6: Reference image.

Figure 7: Input image.

relative scaling r of the input image is 0.966, the tilt

τ =9.22(deg.), the slant ρ =0(deg.), and the rota-

tion angle θ =0(deg.). Figure 8 shows the difference

of the reference image and the recovered image from

the input image using the estimated r, τ , ρ and θ. The

whiter pixels have the larger differences. Comparing

with Figure 9 showing the difference between the re-

covered and original input image, the differences are

reduced greatly by this method. The images compen-

sation by this method is clearly effective.

4 CONCLUSIONS

This paper proposes the method to detect the rela-

tive difference of camera positions (including the dis-

tance, the tilt and the slant) of two images of an

object. In the experiments, it is showed that pro-

posed methods can be applied to the images with

non]homogeneous and non-isotopic textures, such as,

the images of the concrete surface, corkboards and

Figure 8: Difference image (no compensation).

Figure 9: Difference image.

the steel surface. The Proposed method can detect the

differences of camera positions with high accuracy.

Currently we are applying this method to observe the

growth of concrete cracks in an accelerated test envi-

ronment.

REFERENCES

Wen L. Hwang, Chun-Shien Lu, and Pau-Choo Chung.

(1998). Shape from Texture: Estimation of Pla-

nar Surface Orientation Through the Ridge Surfaces

of Continuous Wavelet Transform. IEEE Trans. Im.

Proc., 7(5):773-780.

Eraldo Ribeiro, Edwin R. Hancock. (2000). Texture Plane

Orientation from Spectral Accumulation ICPR.,Vol

I:802-806.

K. Takita, T. Aoki, Y. Sasaki, T. Higuchi, K. Kobayashi.

(2003). High-Accuracy Subpixel Image Registra-

tion Based on Phase-Only Correlation. IEICE Trans.

Fundam. Electron. Commun. Comput. Sci. , E86-

A(8):1925-1934.

VISAPP 2006 - IMAGE ANALYSIS

392