REGISTRATION OF 3D - PATTERNS AND SHAPES WITH

CHARACTERISTIC POINTS

Darko Dimitrov, Christian Knauer and Klaus Kriegel

Freie Universit

at Berlin, Institute of Computer Science

Takustrasse 9, D-14195 Berlin, Germany

Keywords:

Computational Geometry, Pattern Matching, 3D Image Registration.

Abstract:

We study approximation algorithms for a matching problem that is motivated by medical applications. Given

a small set of points P ⊂ R

and a surface S, the optimal matching of P with S is represented by a rigid

transformation which maps P as ‘close as possible’ to S. Previous solutions either require polynomial runtime

of high degree or they make use of heuristic techniques which could be trapped in some local minimum.

We propose a modiﬁcation of the problem setting by introducing small subsets of so called characteristic

points P

⊆ P and S

⊆ S, and assuming that points from P

must be matched with points from S

We focus our attention on the ﬁrst nontrivial case that occurs if |P

| =2, and show that this restriction

results in new fast and reliable algorithms for the matching problem. In contrast to heuristic approaches our

algorithm provides guarantees on the approximation factor of the matching. Experimental results are provided

for surfaces reconstructed from real and synthetic data.

1 MOTIVATION AND RELATED

WORK

Today an increasing number of surgeries is supported

by medical navigation systems. The basic task of such

a system is to transform real world data (positions in

the operating ﬁeld) into a 3-dimensional model (CT

or MR) and to display the transformed position in the

model. Real world data are gaged by optical, elec-

tromagnetic or mechanical tracking systems. A com-

mon technique for computing the transformation is

based on markers which are ﬁxed on bones (land-

mark approach). The markers have to be ﬁxed al-

ready during the model acquisition. Their positions

in the model are computed using appropriate image

processing methods. Later, at the beginning of the

surgery, at least three markers must be gaged with the

tracking system. Since the total number of markers is

small, one could compute the correct matching trans-

formation even by brute force techniques. A more

advanced approach making use of geometric hashing

techniques is presented in (Hoffmann et al., 1999).

There is a strong need to develop algorithmic meth-

ods for computing a transformation without using

markers. The main reason for that is an anatomical

one: in many cases (e.g. spinal surgery) it would be

very hard or even impossible to ﬁx markers before the

surgery. One solution is to gage a few points on the

surface of a bone and to compute the corresponding

points in the model. This point registration is a hard

algorithmic problem, which cannot be solved by the

following standard approaches:

1) A combinatorial search does not work, because the

gaged points could be anywhere on the model surface.

2) Surface matching algorithms do not help, because

the number of gaged points is too small to apply a

surface reconstruction.

There are heuristic methods that could be used,

for example a combination of ICP (Iterative Closest

Point) method with randomly generated starting con-

ﬁgurations. The standard ICP approach, and several

more efﬁcient variants and generalizations of it can

be found in (Besl and McKay, 1992), (Rusinkiewicz

and Levoy, 2001), and (Mitra et al., 2004). However

such heuristic methods have the fundamental draw-

back that they could be trapped in some local mini-

mum, while failing to ﬁnd the optimal solution. In

contrast to this, we will present a registration algo-

rithm that reports all possible registration transforma-

tions satisfying a given quality criterion. This is an

essential property, especially in medical applications.

Matching problems have been studied intensively

393

Dimitrov D., Knauer C. and Kriegel K. (2006).

REGISTRATION OF 3D - PATTERNS AND SHAPES WITH CHARACTERISTIC POINTS.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 393-400

DOI: 10.5220/0001368303930400

 SciTePress

in computational geometry, see (Alt and Guibas,

1999) for an overview. Nevertheless the best known

approaches applicable to our problem require poly-

nomial runtime of high degree (Hagedoorn, 2000).

Since the registration is part of the surgery, real time

algorithms are needed. In contrast to that, it is possi-

ble to spend more time for preprocessing the model.

Here, we try to adapt some ideas of the landmark

approach to that new setting. The role of markers is

played by so-called characteristic points. Such points

can be determined automatically (see next two para-

graphs) or manually, marking some anatomically sig-

niﬁcant points, e.g. the thorn of a vertebra or the root

of the nose. If a set of characteristic points is ﬁxed in

the model and we can track at least three of them, the

old landmark registration algorithms can be applied.

Our main goal is to solve the registration problem if

only two characteristic points can be tracked. To com-

pute the transformation in that case, one must track

some more (non-characteristic) points on the surface.

Different approaches can be applied to ﬁnd char-

acteristic points on the sampled surface. A lot of ef-

fort was devoted on determining the curvature esti-

mation. A comprehensive survey of these methods is

given in (Petitjean, 2002). Popular methods include

quadric ﬁtting, where the estimated curvature is the

one of the quadric that best ﬁts the sampled point lo-

cally. Other methods typically consider some deﬁn-

ition of curvature that can be extended to the poly-

hedral setting. Estimating the curvature by a canoni-

cal mapping between the mesh describing the object

and a standard spherical mesh was done in (Delingette

et al., 1993). More examples of estimating the dis-

crete curvature can be found in (Zhang, 1999), and

(Kim et al., 1999). The deﬁnition of the curvature

tensor in (Cohen-Steiner and Morvan, 2003) is based

on the theory of normal cycles.

Sometimes technics to characterize points of the

surface are strongly related with surface matching

heuristics, e.g. the spin image approach in (Johnson

and Hebert, 1997), surface point signatures in (Ya-

many and Farag, 2002), harmonic shape images in

(Zhang and Hebert, 1999), and ﬁngerprints (Sun and

Abidi, 2001). A method described in (Wang et al.,

2000) is based on geodesic distances in combination

with additional local curvature parameters.

In this paper we present a new geometric approach

to the matching problem with characteristic points.

Some preliminary ideas were already presented in

the form of an extended abstract in (Dimitrov et al.,

2005). In the next section we introduce necessary no-

tations and give a formal deﬁnition of the problem.

In section 3 we present the basic algorithm and show

how to use this method for the approximation of the

optimal matching. Experimental results on real and

synthetic data are provided in section 4, and conclu-

sions and future work are given in section 5.

2 FORMAL PROBLEM

DESCRIPTION

We consider two point sets P and S in R

. Usually

we assume that S is the (inﬁnite) set of points on a

triangulated surface. The corresponding triangulation

will be denoted by S. However, this assumption is

not crucial. The algorithms presented in the next sec-

tions can be applied with small changes if S is a ﬁnite,

dense sample of points on a surface.

Our main goal is to register P into a model S. The

quality of the registration will be evaluated by the di-

rected Hausdorff distance. The distance between a

point a and a compact point set B in d-dimensional

space R

is deﬁned as

dist(a, B) = min

b∈B

||a − b||

where ||·||is the Euclidean norm in R

. For two com-

pact sets A, B in the one-sided Hausdorff distance

from A to B is deﬁned as

−→

H(A, B) = max

a∈A

dist(a, B) = max

a∈A

min

b∈B

||a − b||.

The size of a problem instance (P, S) depends on

two parameters: k, the number of points in P, and n,

the number of triangles in S. We remark that in our

applications k<<ncan be assumed. Moreover, we

assume that two subsets of characteristic points S

⊆

S and P

⊆ P are given. For a precise analysis of

our algorithms we introduce the additional parameters

= |P

| and n

= |S

|. Both parameters should be

seen as some reasonable constants. The special role

of characteristic points is expressed by the additional

requirement, that each p ∈ P

must be mapped onto

(or close to) a characteristic point q ∈ S

First we have to classify several types of matchings.

Deﬁnition 2.1 Given two parameters µ, η ≥ 0 a

rigid transformation T : R

→ R

is called (µ, η)-

matching if the following two conditions hold:

1. µ(T ):=

−→

H (T (P \ P

),S) ≤ µ, and

2. η(T ):=

−→

H(T (P

),S

) ≤ η.

If  is an upper bound for µ(T ) and η(T ) we de-

note T as an -matching. In line with the notations

above, we deﬁne (T ) = max(µ(T ),η(T )). The

minimal (T ) over all rigid transformations T is de-

noted by 

opt

, and a corresponding matching is an op-

timal matching. For a given λ>1, a matching T is a

λ-approximate matching,if(T ) ≤ λ

opt

Furthermore, we introduce the notion of semi-

optimal matchings. To this end we ﬁx a se-

quence

S =(¯s

, ¯s

,...,¯s

) of predeﬁned match-

ing positions for the sequence of characteristic points

,...,p

). We restrict our attention to match-

ings T with T (p

)=¯s

for i =1,...,k

. Let us

VISAPP 2006 - IMAGE ANALYSIS

394

denote this set of matchings by M

. We assume that

and S are congruent, because otherwise M

empty.

A matching T ∈M

is a (µ(T ),η

)-matching,

where η

−→

H (S,S

) is a common value for all

matchings in M

. A matching T ∈M

is called

semioptimal matching (with respect to

S)ifµ(T ) is

minimal.

A trivial case with |M

| =1occurs, if P

contains

three or more non-collinear points. Thus, we will fo-

cus our attention to matchings with two characteristic

points. In a ﬁrst step we design an algorithm to com-

pute semioptimal matchings for a given set

S. Then,

based on the semioptimal solution, we show how to

compute a λ-approximate matching for any λ>1.

3 THE 2 POINT CASE

3.1 Semioptimal Matchings

In general a rigid transformation in 3-dimensional

space has six degrees of freedom: three for ﬁxing a

translation and three more describing a rotation. The

ﬁrst step of our approach is devoted to a very special

case with one degree of freedom only. Assuming a

pair

S =(s

, s

) of predeﬁned matching positions

for the two characteristic points p

, the matchings

in T ∈M

have a ﬁxed translation (T (p

)=s

)

and two ﬁxed parameters of the rotation (mapping the

axis (p

) to the axis (s

, s

)). Thus, it remains to

consider all rotations around the axis (

, s

). First,

we present an algorithm which reports (for any µ) all

transformations T ∈M

with µ(T ) ≤ µ.

Basic Algorithm (Outline)

1. Fix a rigid transformation T

: R

→ R

such that T

)=s

. For all

∈ P \{p

} let C

= C(p

) be the circle with

the following properties (see ﬁgure 1):

• the center of C

is on the line deﬁned by p

and

• C

lies in a plane perpendicular to p

, and

• p

is on C

2. Consider the transformed circle T

) and let

the point p



(α) rotate along this circle starting

from T

), i.e., p



(0) = T

). Compute sets

of intervals I

= {α |dist(p



(α),S) ≤ µ}, for

i =3,...,k.

3. Compute I = ∩

i=3

. For each α ∈ I let R

(s, s



)

be the rotation around axis

s, s



with angle α. Then

:= R

(s, s



) ◦T

is a rigid transformation with

µ(T

) ≤ µ.

Figure 1: Corresponding points and the rotation of the point



An obvious upper bound for the run time complex-

ity of the algorithm is almost straightforward. To ﬁnd

the range of angles, for which the circle is at most µ

near to a triangle, we compute the intersection of the

circle and the Minkowski sum of the triangles and a

ball with radius µ centered at the origin of the coor-

dinate system. Computing such an intersection costs

O(1) time. In the worst case it should be repeated

for all n triangles. To compute one particular interval

we sort and merge the O(n) intervals, O(1) con-

tributed from each triangle, which cost O(n log n).

Computing the intersection I can be done in O(n)

time in a sweep line manner. This altogether gives

the following bound:

Lemma 3.1 The run time complexity of the basic al-

gorithm presented above is O(knlog n).

The basic algorithm can be used as a decision al-

gorithm answering the question whether for a given µ

there is some matching T with T (p

)=s, T (p



and µ(T ) ≤ µ for all other points of P . Thus,

using binary search one can approximate a semiopti-

mal matching. However, it is also possible to com-

pute the precise value µ of a semioptimal match-

ing by the following modiﬁcation of the basic algo-

rithm. Instead of computing the interval sets I

{α | dist(p



(α),S) ≤ µ}, we compute the functions

(α):=dist(p



(α),S). This function is the lower

envelope of the distance functions of a rotating point

to the surface triangles. Then, instead of computing

I = ∩

i=3

, we compute the upper envelope f of all

functions f

. The minimum of f is the µ-value of a

semioptimal matching.

To determine the description complexity of f it is

necessary to apply the theory of Davenport-Schinzel

sequences, see (Sharir and Agarwal, 1995). Because

the detailed analyizes is beyond the scope and space

of this paper, we only mention the main facts. Each

function f

is the lower envelope of n distance func-

tions between a point on a circle and a triangle. So,

the total number of functions contributing to f is

O(kn). The distance function between a point on a

circle and a triangle can be described piecewise by

polynomials of degree 4. The envelope f of O(kn)

REGISTRATION OF 3D - PATTERNS AND SHAPES WITH CHARACTERISTIC POINTS

395

such polynomials is related to a (kn,4)-Davenport-

Schinzel sequence, whichs maximal length is bounded

from above by O(kn h(kn)), where h(kn) is a very

slowly growing sublogarithmic function. In divide-

and-conquer manner, see (Sharir and Agarwal, 1995)

for details, we can compute the envelope f in time

O(knh(kn) log kn), which is also the upper bound

for time complexity of the semioptimal matching.

Lemma 3.2 The run time complexity of the algo-

rithm for computing a semioptimal matching is

O(knh(kn) log kn).

3.1.1 Improving the Run Time Complexity

Both run time bounds above are dominated by the

fact, that for a point rotating on a circle C

the dis-

tance to all triangles of the surface is taken into ac-

count. However, for computing the intervals I

on a

circle that are close to the surface it is sufﬁcient to

consider only the triangles that are close to the circle.

In reality these triangles form only a small subset of

the whole surface. The same applies for the compu-

tation of the distance functions f

:[0, 2π] −→ R

that can be restricted to the range of angles where the

corresponding points are close to the surface.

Thus, we aim at the construction of a data struc-

ture supporting queries for triangles close to a given

point. We adapt a well known approach subdivid-

ing the bounding box of the surface S by equidistant

planes parallel to the xy-,xz- and yz-plane. In a ﬁrst

step we compute for each subbox the list of all trian-

gles intersecting that box.

In the main procedure the distance between a point

and the surface is computed by point location in the

grid of subboxes and checking only the triangles asso-

ciated with the located subbox or with its neighboring

subboxes. Using an m × m × m grid the expected

number of triangles to be checked is reduced from

n to

27n

. It is clear that such an average argument

does not help in a worst case analysis, and indeed, one

can construct surfaces with very large triangle lists in

many subboxes. However, accepting some reasonable

assumptions on the surface representation it will be

possible to prove some useful upper bounds. Since

this analysis is technically involved (and not in the

main focus of a computer vision conference) we will

restrict ourself to sketch the main ideas needed for

that proof.

We consider a triangulated surface S given by n

triangles and denote the minimal and maximal lengths

of triangle edges by l and L. We will call S a well

represented surface with respect to global constants

(independent of n) c

≥ 1,c

> 0,c

≥ 1,c

∈

N, 0 <α≤ π/3, if the following properties hold:

1. Shape property: The three side lengths of the

bounding box B of S differ at most by the factor c

and the projection of S to at least one of the three

side planes of B covers at least a c

fraction of the

side plane area.

2. Edge ratio:

≤ c

3. Stabbing density: Any line segment of length l in

the space intersects at most c

triangles.

4. Fatness: All triangles are α-fat, i.e. all angles are

at least α.

We would like to stress that most surfaces encoun-

tered in the practice satisfy above properties.

Theorem 3.3 If S a well represented surface is sub-

divided into a

√

n ×

√

n ×

√

n grid of subboxes then

any subbox is intersected by at most a constant num-

ber of triangles. This constant depends only on the

constants in the deﬁnition above

Since any circle in space intersects at most O(

√

subboxes we obtain a sublinear runtime for both, the

basic algorithm and the algorithm for semioptimal

matching.

Lemma 3.4 If S is a well represented surface sub-

divided into a

√

n ×

√

n ×

√

n grid of subboxes

then the run times complexity of the basic and

semioptimal matching algorithms are O(k

√

n log n)

and O(k

√

nh(k

√

n) log kn), respectively. The pre-

processing time is O(n

1.5

We remark that the properties edge ratio and fat-

ness can be relaxed in such a way that they can be

violated by O(

√

n) triangles. In that case theorem 3.3

holds only for the number of nonviolating triangles,

but we obtain the same run time bound as above.

Finally, we remark that the

√

n×

√

n×

√

n grid size

was chosen particularly with regard to best possible

results in the theoretical run time analysis. In practical

experiments already 20 × 20 × 20 grids proved to be

very useful.

3.2 The Approximation Problem

There are two groups of standard approaches for

approximating an optimal solution starting from

some initial solution. The ﬁrst group consists of

heuristic approaches, including simulated annealing

(van Laarhoven and Aarts, 1987) and ICP variants

(Rusinkiewicz and Levoy, 2001), (Mitra et al., 2004).

These methods have proved to be useful in many prac-

tical situations, but, it is hard to prove something

about the quality of the approximation in the worst

case. The algorithm from the second group are based

on a method capable to compute initial solutions that

are provably close to the optimal solution, and on a

dense discretization pattern around the initial solu-

tion.

Our approach belongs to the second group. First we

compute a semioptimal matching T as a initial solu-

tion, such that (T ) ≤ C ·

opt

, where C is a constant.

VISAPP 2006 - IMAGE ANALYSIS

396



= u = u

= v = v

o o



Figure 2: The positions of the points t, s

and s

after applying the transformations R

. Points x, x

are the

nearest points on the surface S of the points t, t

correspondingly.

Then, for any given λ>1, we construct a grid-like

pattern around the initial solution such that at least

one of the grid points represents a λ-approximation

of the optimal matching. The density of the grid (and

consequently the size of the grid pattern) will depend-

ing only on λ and on (T ).

A common key problem of many approximation

problems focuses on the fact the the value of an op-

timal solution is unknown. Here we are able to de-

rive upper and lower bounds for 

opt

from the re-

sults of some semioptimal matchings. Since each

pair (s, s



) of characteristic points on S could consti-

tute the approximated destination of (p

) we ap-

ply this procedure for each such pair. More precisely,

we compute the semioptimal matching T

s,s



mapping

) onto the point pair (s

, s

), where (s

, s

)

forms the same line and has the same center as (s, s



but ||

−s

|| = ||p

−p

||. We denote the qualities of

these semioptimal matchings by δ

s,s



= (T

s,s



) and

the best value by δ = min{δ

s,s



| s, s



∈ S

}. Fur-

thermore, we introduce the radius r

and the relative

radius ρ

of the point set P with respect to the center

of the characteristic points as follows:

= max

p∈P

− p||,

||p

−p

2 r

||p

−p

(1)

Obviously, ρ

≥ 1.

Proposition 3.5 δ ≥ 

opt

≥

Proof The upper bound for 

opt

is trivial, because the

best semioptimal matching cannot be better than the

global optimum.

To prove the lower bound, let T

opt

denote the optimal

matching. According to the deﬁnition there are two

characteristic points s, s



∈ S

such that ||T

opt

) −

s|| ≤ 

opt

and ||T

opt

) − s



|| ≤ 

opt

. We consider

the semioptimal matching T

s,s



and the additional

transformation T

add

transforming T

s,s



into T

opt

. Ob-

viously one can decompose T

add

into two rotations

and one translation T

add

= T ◦R

◦ R

, where

• the ﬁrst rotation R

is around the axis spanned by

s and s



• the second rotation R

is around an axis through

the center o of the segment ss



and orthogonal to

this segment,

• and T is a unique, ﬁnal translation.

We have T

opt

= T

◦R

◦T

s,s



and δ = (T

s,s



) ≤

(R

◦T

s,s



) because T

s,s



was semioptimal and R

a rotation around (s, s



). Thus, there is a point p ∈ P

such that the distance of (R

◦T

s,s



)(p) to the surface

S is at least δ. To avoid double indices let us introduce

the following notations, see ﬁgure 2 for illustration:

u := s

, v := s

and t := T

s,s



(p). Furthermore, we

set u

:= R

(u),u

:= R

),u

:= T (u

) and

analog notations for v and t. Finally, let x

, and

be the closest points on the surface to t

, and

. From the observations above we know that

δ ≤ δ

s,s



≤t

− x

. (2)

Since x

is the closest point on S to t

,wehave

t

− x

≤t

− x

 and applying the triangle in-

equality we obtain:

t

−x

≤t

−x

≤t

−t

+t

−t

+t

−x

.

(3)

Now we estimate the three terms on the right side of

the inequality above. Since t

is the image of a point

p ∈ P under T

opt

we get

t

− x

≤

opt

. (4)

Then distance between t

and t

= R

) depends

on the distance d of t

to the rotation axis and the an-

gle of the rotation. Clearly, d is bounded from above

by the distance to the center o of the segment (s, s



)

and the angle of rotation is the same as for turning u

to u

. Thus,

t

−t



u

−u



u

−o

≤

t

−o

u

−o

≤ ρ

and

t

− t

≤ρ

u

− u

. (5)

We remark that the translation T applied to u

and v

increases the distance between u

and s, or the dis-

tance between v

and s



and thus

REGISTRATION OF 3D - PATTERNS AND SHAPES WITH CHARACTERISTIC POINTS

397

2δ

Figure 3: Two grids around the points s



and o.

u

− u

≤s − u

 = s



− v



≤ max (s − u

, s



− v

)

≤ 

opt

(6)

The same argument yields u

−u

≤

opt

and since

T is a translation

t

− t

 = u

− u

≤

opt

. (7)

It remains to merge (2) with (3) and to plug in (4), (5),

(6) and (7) into the right hand side of (3):

δ ≤t

− x



≤t

− t

 + t

− t

 + t

− x



≤ ρ

· 

opt

+ 

opt

+ 

opt

=(2+ρ

)

opt

It follows that 

opt

≥

. 

Given an approximation factor λ>1 we try to

improve the best value δ obtained so far by small

changes of the predeﬁned matching positions

, s

The bounds above can be used to design a grid based

set of perturbed matching positions which is dense

enough to include a λ-approximation of an optimal

matching. Let us decompose the transformation,

which leads from one of the semioptimal matchings

to the optimal matching, into the rotational and

translational component. A spherical squared grid

centered at the point

determines the rotational com-

ponent, and a cubic grid centered at the point o deter-

mines the translation component, see ﬁgure 3. The

total size of the spherical grid (the angle α), and the

size of the cubic grid depend on δ, namely, α =

2δ

p

−p



and the spherical grid size is 2δ. This

choice ensures that the optimal matching is within the

range of that scheme. The subdivision of the spher-

ical grid is deﬁned by an angle β =

(λ−1)δr

(ρ

+2)

and

the cells of the cubic grid have side length

√

3(λ−1)δ

3(ρ

+2)

It can be veriﬁed easily that such an approximation

scheme is ﬁne enough to provide for a semioptimal

matching that is at most (λ − 1)

opt

far from its opti-

mal matching position.

Consequently, the number of the grid combina-

tions, deﬁning possible matching positions (

, s

),is

(

√

3ρ

(ρ

+1)

λ−1

+1)

(

√

3(ρ

+1)

λ−1

+1)

. This implies

the following estimation of the total run time:

Lemma 3.6 The run time complexity of

the λ-approximation presented above is

O(n

knh(kn) log (kn)

(λ−1)

We remark that the factor n in this formula can be

improved in the same way as discussed in the analy-

sis of the semioptimal matching in the section 3.1.1.

Moreover, in the applications the ratio ρ

can be re-

garded as a small constant.

4 EXPERIMENTAL RESULTS

We have implemented a variant of the semiopti-

mal matching algorithm with the subdivided bound-

ing box data structure as described in section 3.1.

The maximal size of the subbox structure was set to

20 × 20 × 20, which compared with the theoretically

optimal one (

√

n ×

√

n ×

√

n) decreases the pre-

processing time (creating and initializing of the sub-

box data structure), but increases the matching time.

Usually, in the medical navigation applications, there

is enough time for preprocessing, so one can build a

ﬁner subbox structure to increase the matching time.

Time efﬁciency, preciseness and robustness of the al-

gorithm were veriﬁed on real and synthetic data. The

surfaces S were reconstructed by scans acquired by

MR, CT and range scanner devices, or were gener-

ated synthetically. As it is a case with most surfaces

encountered in the practice, our test surfaces are also

well deﬁned in a sense described in 3.1.1. An exam-

ple of the head test model reconstructed by MR scan

data is given in ﬁgure 4. The set P was generated

in the following manner: ﬁrst, some very small sub-

set P

of points from the surface S was randomly se-

lected, s.t. two of the points were characteristic points

and the rest some arbitrary points from the surface S.

Then, the points from P

were randomly perturbed

VISAPP 2006 - IMAGE ANALYSIS

398

Figure 4: Registration of the head model. The characteristic points are denoted with crosses, and the non-characteristic ones

with circles.

Table 1: Some relevant parameters of the tested models. The last parameter shows the size of the subcube structure build

around the models.

model # of faces |s

| avg. edge length diameter # of subboxes

head 358784 10 0.988736 330.193 5120

bunny 69451 10 0.001471 0.25025 6400

cow 5804 10 0.021878 1.27111 1820

cat 671 6 0.014992 0.27041 3520

forming point set

. Finally, point set

was trans-

formed with a random rigid transformation T

, i.e.

P = {T

(˜p

) | ˜p

∈

The algorithm was tested both on noiseless and

noisy data. The tests were performed on P3,

1.27 GHz, 512 MB RAM - PC. To estimate the qual-

ity of the registration we used the following 3 mea-

sures:

• measure1 = max

 ˜p

−T

out

)

diameter(S)

= max

 ˜p

−T

out

(˜p

))

diameter(S)

• measure2=

−→

H (T

out

(P )S)

diameter(S)

• measure3 = max

i,j,i=j

(|1 − a

|, |0 − a

|),

∈ M

out

× M

where T

out

is the output transformation given by our

algorithm, which matches the point set P with the

surface S, and M

out

and M

are the corresponding

matrices of the rigid transformations T

out

and T

re-

spectively.

The results (see tables 2, 3) show that the imple-

mentation of the semioptimal algorithm is fast, ro-

bust and gives accurate matchings. Eventual further

improvements of the accuracy can be achieved with

the λ-approximation algorithm described in the sec-

tion 3.2. Its implementation is one of the tasks for the

future. Alternatively, one can use another heuristical

approaches to improve the matching, although, as it

was previously mentioned, there is no guarantee what

kind of approximation of the optimal matching will

be achieved.

5 CONCLUSION AND FUTURE

WORK

We have given an efﬁcient algorithms for matching a

point set and a surface, both with characteristic points.

The ﬁrst nontrivial case, when the point set has two

characteristic points, was considered. We design an

algorithm which assumes that the matching positions

of both characteristic points are known. Based on

it, we show how a λ-approximation of the optimal

matching can be computed. An implementation of

this algorithm was tested on real and synthetic data,

demonstrating its efﬁciency, robustness and accuracy.

We would like to stress that with slight modiﬁcation

of the algorithms and analysis, we can extend our re-

sults and match arbitrary point sets and shapes with

characteristic points in 3 space. The analysis shows

that the presented algorithm is competitive in com-

plexity with the solutions we have for solving the

approximate matching problem when 3 characteristic

point are known.

Further work will consist in implementation of the

grid scheme needed for the λ-approximation algo-

rithm, and designing and implementing a solution of

the matching problem when the point set contains

only one characteristic point.

REGISTRATION OF 3D - PATTERNS AND SHAPES WITH CHARACTERISTIC POINTS

399

REFERENCES

Alt, H. and Guibas, L. (1999). Discrete geometric shapes:

Matching, interpolation, and approximation. In Sack,

J.-R. and Urrutia, J., editors, Handbook of Computa-

tional Geometry, pages 121 – 153. Elsevier Science

Publishers B.V. North-Holland, Amsterdam.

Besl, P. J. and McKay, N. D. (1992). A method for registra-

tion of 3-d shapes. IEEE Trans. on Pattern Recogni-

tion and Machine Intelligence, 14(2):239–256.

Cohen-Steiner, D. and Morvan, J.-M. (2003). Restricted

delaunay triangulations and normal cycle. In Proceed-

ings of the 19th Annual ACM Symposium on Compu-

tational Geometry, pages 237–246.

Delingette, H., Hebert, M., and Ikeuchi, K. (1993). A spher-

ical representation for the recognition of curved ob-

jects. International Conference on Computer Vision,

pages 103–112.

Dimitrov, D., Knauer, C., and Kriegel, K. (2005). Match-

ing surfaces with characteristic points. In Proceed-

ings of the 21th European Workshop on Computa-

tional Geometry (EWCG), Eindhoven, Netherlands.

Hagedoorn, M. (2000). Pattern matching using similarity

measures. PhD thesis, Utrecht University.

Hoffmann, F., Kriegel, K., Sch

onherr, S., and Wenk, C.

(1999). A simple and robust algorithm for landmark

registration in computer assisted neurosurgery. Tech-

nical report, Freie Universit

at Berlin.

Johnson, A. and Hebert, M. (1997). Surface registration by

matching oriented points. International Conference

on Recent Advances in 3-D Digital Imaging and Mod-

eling, pages 121–128.

Kim, S.-J., Jeong, W.-K., and Kim, C.-H. (1999). Lod gen-

eration with discrete curvature error metric. In 2nd

Korea Israel Bi-National Conference on Geometrical

Modeling and Computer Graphics in the WWW Era,

pages 97–104.

Mitra, N. J., Gelfand, N., Pottmann, H., and Guibas, L.

(2004). Registration of point cloud data from a geo-

metric optimization perspective. In Symposium on

Geometry Processing, pages 23–32.

Petitjean, S. (2002). A survey of methods for recover-

ing quadrics in triangle meshes. ACM Comput. Surv.,

34(2):211–262.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants of

the icp algorithm. In Third International Conference

on 3D Digital Imaging and Modeling, pages 145–152.

Sharir, M. and Agarwal, P. (1995). Davenport-Schinzel se-

quences and their geometric applications. Cambridge

University Press.

Sun, Y. and Abidi, M. A. (2001). Surface matching by 3d

point‘s ﬁngerprint. In IEEE Int. Conf. On Computer

Vision, vol. II, pages 263–269.

van Laarhoven, P.-J.-M. and Aarts, E.-H.-L. (1987). Simu-

lated Annealing: Theory and Applications. D.Reidel

Publishing Company, Kluwer.

Wang, Y., Peterson, B. S., and Staib, L. H. (2000). Shape-

based 3d surface correspondence using geodesics and

local geometry. Computer Vision and Pattern Recog-

nition, 2:2644–2651.

Yamany, S. M. and Farag, A. A. (2002). Surfacing signa-

tures: An orientation independent free-form surface

representation scheme for the purpose of objects reg-

istration and matching. IEEE Transactions on Pattern

Analysis and Machine Intelligence 24(8), pages 1105–

1120.

Zhang, D. (1999). Harmonic Shape Images: A 3D Free-

form Surface Representations and Its Applications in

Surface Matching. PhD thesis, Carnegie Mellon Uni-

versity.

Zhang, D. and Hebert, M. (1999). Harmonic maps and their

applications in surface matching. In Computer Vision

and Pattern Recognition, volume 2, page 2524.

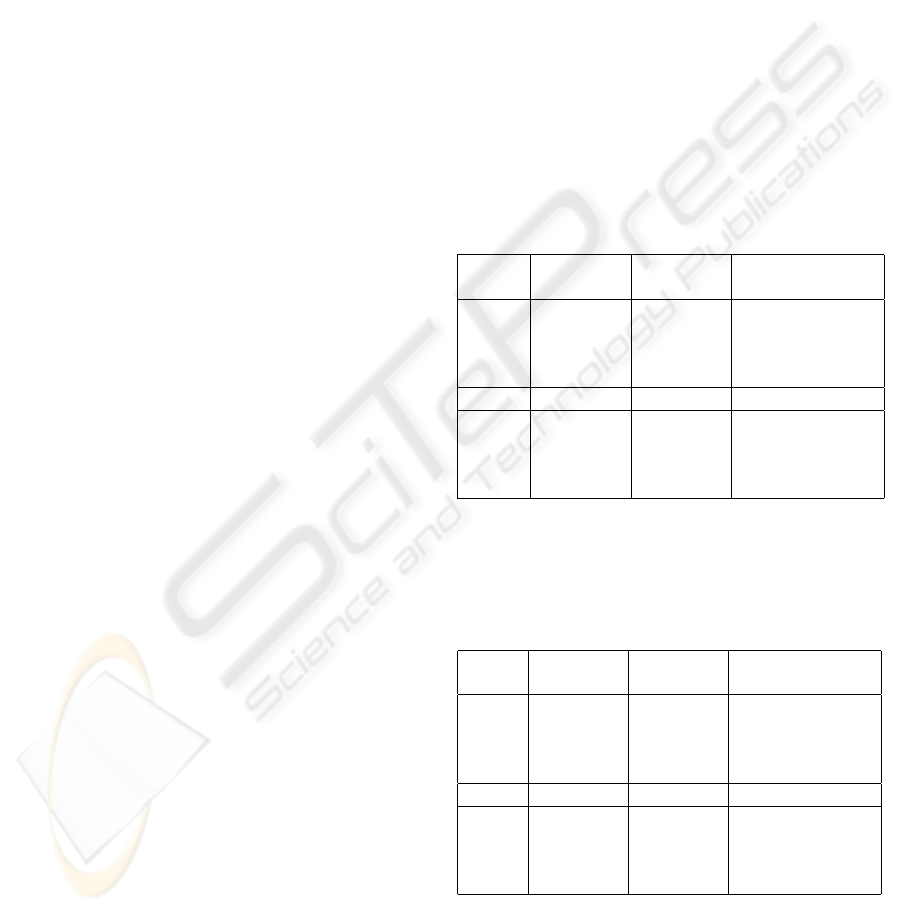
Table 2: Experimental results on noiseless data. The values

in the table are the average of the results of 100 runs of the

algorithm, each time with a newly generated point set P .

model preproc. matching # of calls of the

[s] [s] basic algorithm

head 11.433 21.556 6

bunny 2.433 4.556 7

cow 0.201 1.771 5

cat 0.04 0.951 2

measure1 measure2 measure3

head 0.000748 0.000103 0.0000037

bunny 0.004483 0.000203 0.0000663

cow 0.005954 0.001869 0.0032076

cat 0.009801 0.000899 0.0028853

Table 3: Experimental results on noisy data of the head

model. Random noise, between 0 and noise factor*average

edge length, was added to the points from P . The values

in the table are the average of the results of 100 runs of the

algorithm, each time with a newly generated point set P .

noise preproc. matching # of calls of the

factor [s] [s] basic algorithm

0 11.433 21.556 6

1 11.386 21.281 6

5 11.425 22.771 5

10 11.375 22.609 3

measure1 measure2 measure3

0 0.000748 0.000103 0.0000037

1 0.008512 0.000703 0.0000067

5 0.015954 0.001869 0.0032076

10 0.036983 0.210899 0.0048853

VISAPP 2006 - IMAGE ANALYSIS

400