
LOCAL MINIMUM DISTANCE FOR THE DENSE DISPARITY
ESTIMATION
Eric Alvernhe
EMA, Lgi2p
N
ˆ
ımes, France
* Philippe Montesinos, *Stefan Janaqi,† Min Tang
*EMA Lgi2p,+Nanjing university of science and technology
*N
ˆ
ımes France, †Nanjing China
K
eywords:
Stereo, Dense disparity map, Partial derivative equations, minimum distance.
Abstract:
This paper presents a new algorithm to solve the problem of dense disparity map estimation in stereo-vision.
Our method is an iterative process inspired by variationnal approach. A new criteria is used as the attachment
term based on the distance to local minimum of a similarity measure. Our iterative process is heuristic. Nev-
ertheless, we are able to interpret this algorithm presenting both combinatorial and continuous characteristics.
The quality and precision of the results obtained by our method both on image benchmarks and real data
clearly demonstrate the the validity of this approach.
1 INTRODUCTION
The aim of stereo-vision is to give a perception of a
scene in three dimensions using two or several im-
ages taken from different points of view. Usually,
stereo-vision is used to compute three dimensions re-
construction of rigid scenes. In order to solve this
problem, we need first to compute matches between
features of the given images. This paper focuses on
stereo-vision image matching.
Matching problem often appears in various vision
tasks such as: motion, image registration, pattern
recognition, and stereo-vision. Unfortunately, each
similarity measure that can be defined gives a percent-
age of false matching due to noise and ambiguity. In
sparse stereo matching, we often concentrate on fea-
tures or image primitives such as points of interest,
segments, regions. As an example, points of inter-
est (Gouet et al., 1998) are especially chosen for their
neighborhood specificity to reduce matching ambigu-
ity (points of interest are frequently used to recover
the epipolar geometry in uncalibrated stereo-vision).
Generally a matching scheme proceed in two steps,
a first step of computing scores of similarity and a
second step of relaxation involving geometrical infor-
mations able to deal with ambiguous and weak corre-
spondances.
In this paper, we are interested in dense correspon-
dences i.e correspondences of all non occluded pix-
els of the image. The matching of image features
have obtained a lot of attention in the literature see
(Scharstein et al., 2001). The results of all these meth-
ods can be compared on the basis of the disparity
maps that they can deliver. Roughly speaking, dis-
parity is a value related to the displacement of pixels
from one image to another, and the disparity map con-
tains the disparity value of all the matching pixels (a
precise definition of disparity will be given in the next
section).
Different characteristics allow to give the speci-
ficity of dense matching in comparison to the sparse
one:
• Disparity map is defined over the entire image do-
main. It has to be a piecewise continuous function
preserving the edge’s depth.
• Concerning the improvement of the ambiguous
matches (as in textured region for example), relax-
ation cannot be done over the entire image domain
for obvious computational reasons. It is the role of
a global regularization constraint to overcome this
problem.
Features like segments or corners points (Boufama
and Jin, 2002) have been intensively studied for
stereo-vision but they cannot lead to precise dense
disparity maps, principally due to the fact that these
features do not appear on the homogeneous areas of
the images. The use of regions for matching is dif-
ficult because of the lack of robustness of the char-
acterization of regions under projective transforma-
341
Alvernhe E., Montesinos P., Janaqi S. and Tang M. (2006).
LOCAL MINIMUM DISTANCE FOR THE DENSE DISPARITY ESTIMATION.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 341-348
DOI: 10.5220/0001369803410348
Copyright
c
SciTePress

tions. Dynamic programming often focuses on the
study of specific lines in the image (i.e the epipolar
lines presented in the next section) doing a combi-
natorial search for matches. This search has to sat-
isfy a regularity constraint on these lines and between
them (Ohta and Kanade, 1985). The satisfaction of
this constraint, while preserving edges, remains a dif-
ficult task.
With the development of the Partial Derivative
Equations (PDE) and the increase of the computa-
tional speed, a new strategy based on a variational ap-
proach has been proposed by (Alvarez et al., 2000).
Their scheme naturally introduces a global regularity
constraint and a depth edge constraint into the varia-
tional formulation. After solving the Euler-Lagrange
equation they obtain a PDE composed of two terms: a
regularization term and an attachment term. As their
PDE is a gradient descent of an energy functional,
it is very important to have an energy “as convex as
possible”. For this reason, they use a coarse-to-fine
approach based on a multi-scale gaussian smoothing,
and at each scale, they compute a disparity map. At
the end of this process they obtain the final disparity
map.
Recently (Maier et al., 2003) has proposed a non
hierarchical approach which takes into account the
edges accurately. In (N.Slesareva et al., 2005) the
authors propose to use a Total Variation regularization
(Blomgren, 1998) and an attachment term coming
from the optical flow literature. This method seems
to give promising results especially for noisy images.
We propose a new scheme allowing to compute di-
rectly the disparity map without multi-scale approach.
As the other methods our approach involves two terms
of regularity and data attachment. As regularity term,
we use the regularity constraint of (Alvarez et al.,
2000), but for the attachment term, in order to over-
come the problem of numerous local minima (one of
the characteristics of the dense matching), we use the
signed distance to the local minima given by a sim-
ilarity measure. With this modification, our scheme
is no more deduced from a variational method but,
the iterative process that we have defined has heuris-
tic justifications:
• All pixels minimizing a given similarity measure
are candidates for matching and have the same im-
portance. For the non ambiguous pixels, the match-
ing candidate is often unique and will be the first
match found by our iterative process. For ambigu-
ous ones (as in textured region) the regularity con-
straint is used to improve the matches.
• Local minima of the similarity measure which are
close to each other collapse into one in the set
of matching candidates for our attachment term.
The resulting winning position is the one with the
P
p1
C1
C2
l1
l2
p2
Figure 1: Epipolar constraint: plane (P, C
1
,C
2
) intersects
l
1
and l
2
and p
1
and p
2
are projections of P on the images.
p
1
and p
2
lie on the epipolar lines.
smallest disparity measure.
Our regularisation term is continuous, while the at-
tachement term can be considered as combinatorial
by its discrete valuations. In the following of this pa-
per our method will be referenced as Iterative Scheme
to Local Minima (ISLM). Note that the combinatorial
aspect of our method is not implemented as a kind of
relaxation, but by properties of the valuation of our
attachment term.
The paper is organized as follows: section 2
presents the epipolar constraint and the disparity map.
Section 3 presents PDE based on variational approach
(Alvarez et al., 2000). The role of Nagel-Enkelmann
operator, used in our work, as a diffusion-reaction
term preserved discontinuity will be explained here.
Section 4 presents our attachment term and its prop-
erties, we discuss the differences with the Alvararez
variational approach. Our generic attachment term
can be computed with different similarity measures,
and we present here a simple square difference on
a correlation mask. Section 5 develops the compu-
tation of our attachment term. Finally, in section
6 experimentations are presented. We use synthetic
data where the true disparity is known and also real
images. The pertinence of our approach is demon-
strated by quantitative results when the true disparity
is known, and by qualitative results otherwise.
2 EPIPOLAR GEOMETRY AND
DISPARITY ESTIMATION
We note by I
1
and I
2
the two different views of a rigid
scene. Each three-dimensional point P of the scene
form a plane with the two optical centers C
1
and C
2
.
The intersection of this plane and the retinas are
lines, respectively l
1
and l
2
called epipolar lines. The
epipolar constraint expresses the fact that pixels p
1
and p
2
, which are respectively the projections of P on
I
1
and I
2
, lie respectively on l
1
and l
2
(see Figure (1)).
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
342

Lambda
x1
y
1
x2
y
2
o
x2
p1
p2
Figure 2: λ is the signed distance from projection o of p
1
on epipolar line l
2
to p
2
.
In practice, the epipolar constraint allows the re-
duction of the search space for a corresponding pixel
of p
1
(image I
1
) to the line l
2
instead of all the im-
age domain I
2
. As a consequence, epipolar constraint
increases the matching quality and the computational
speed. This constraint is algebraically expressed by
the fundamental matrix 3 × 3 F .
We have:
F.
t
(x
1
,y
1
, 1) =
t
(a
2
,b
2
,c
2
) (1)
with
a
2
x
2
+ b
2
y
2
+ c
2
=0 (2)
where, p
1
=
t
(x
1
,y
1
, 1) and p
2
=
t
(x
2
,y
2
, 1) are
projective pixels coordinates,
t
(a
2
,b
2
,c
2
) represents
the equation of l
2
. So, the epipolar constraint can be
written as:
(x
2
,y
2
, 1) F
t
(x
1
,y
1
, 1) = 0 (3)
In the following, we will consider that the funda-
mental matrix is known, (see for fundamental matrix
computation (Torr and Murray, 1997; Zhang et al.,
1994)).
We need to estimate the disparity of all the pixels.
Disparity for a pixel p
1
is a two dimensional affine
vector h = p
1
p
2
in the image I
2
(keeping coordinates
of p
1
from the image I
1
). Thanks to the fundamental
matrix, only one coordinate of this vector needs to be
memorized. If we note o the projection of p
1
on l
2
,
we have h = p
1
o + op
2
with:
p
1
o =
p
1
Fp
1
a
2
2
+ b
2
2
(4)
Using the fundamental matrix, disparity h can be
defined only by op
2
which will be referred as λ in
the following (see figure (2)). Thus, our dense stereo
correspondence problem is reduced to the estimation
of a grey level image λ over the image domain chosen
to be I
1
.
3 A VARIATIONAL APPROACH
FOR STEREO-VISION
This section presents the variational minimization ap-
proach introduced by (Alvarez et al., 2000) in order
to solve this stereo-vision problem. We explain there
the role of the Nagel-Enkelmann operator.
The functional energy E
var
model classically con-
tains two terms:
E
var
(λ)=CE
Regular
(∇λ)+E
Attach
(λ) (5)
In order to minimize this functional we can use a
gradient descent strategy after discretization with the
corresponding PDE:
dλ(t)
dt
= −∇E
var
(λ(t)) (6)
We note here λ(t) the image obtained after t iter-
ations of the gradient descent. To obtain a good dis-
parity result with this PDE, two conditions must be
verified:
• The disparity image corresponding to the global
minimum of the energy must be close to the
true disparity one, the minimization of variational
method (eq. 5) is well designed to our stereo prob-
lem.
• The λ
tmax
solution obtained by the PDE (6) has to
be the global minimum of the variational function
(5).
To avoid local minima of their PDE, the authors
use a coarse-to-fine hierarchical approach based on
gaussian smoothing, see (Alvarez et al., 2000) for
more details. Now we are going to discuss the first
condition just stated before.
3.1 A Definition of Energy
We note Ω the entire image domain defined with vari-
able x and y and
I
λ
(x, y):=I((x, y)+h(λ))
The equation (eq. 5) is composed of two terms of
different weights C and 1.
The regularization term is defined as follows:
E
Regular
=
Ω
1
|∇(I
1
)|
2
+2ν
2
t
∇λD(∇I
1
) ∇λdxdy
(7)
with :
D(∇I
1
)=
−
∂I
1
∂y
∂I
1
∂x
−
∂I
1
∂y
∂I
1
∂x
+ ν
2
Id
(8)
The attachment term is:
E
Attach
(λ)=
Ω
(I
λ
1
(x, y)−I
2
(x, y))
2
dx dy (9)
The PDE obtained by the Euler-Lagrange condi-
tions from equation (5) is:
LOCAL MINIMUM DISTANCE FOR THE DENSE DISPARITY ESTIMATION
343

dλ
dt
=
Ω
Cdiv(D(∇I)∇λ)+
(I
λ
1
(x, y) − I
2
(x, y))
a
2
∂I
λ
1
∂y
+ b
2
∂I
λ
1
∂x
a
2
2
+ b
2
2
dx dy
with reflecting boundary conditions.
The role of these two terms of the PDE in our stereo
problem is:
• The minimization of the attachment term implies
that the matches must have close intensity values,
according to a lambertian hypothesis.
• The minimization of regularization term imposes a
continuity constraint in the disparity image. In ho-
mogeneous regions the disparity should be contin-
uous with a step at the depth edges.
More details of the Nagel-Enkelmann reaction-
diffusion operator used for the regularization process
will be presented in the next subsection. The differ-
ent attachment terms will be discussed in detail in the
section 4.
3.2 Nagel-Enkelmann Operator
Nagel-Enkelmann operator has received a lot of
attention in computer vision, especially for optical
flow analysis(Nagel, 1983). From a physical point
of view, it can represent the behavior of the heat
distribution in an isolated volume (with neglected
convexion). We give an example in the figure (3),
where we compute Nagel-Enkelmann diffusion in a
“Florence flask”.
The initial heat distribution is given at the image
heat
t
0
and the flask is associated to an image Flask.
Note that the heat diffusion is isotropic inside the
Florence flask, and is stopped by reaction at the edge.
We will briefly explain the equivalence between
this diffusion-reaction and our problem. Then we
will discuss the role of each element of the Nagel-
Enkelmann operator.
The heat(x, y), intensity value is the heat at the
point (x, y) corresponding to the disparity λ(x, y)
in our stereo problem, and I
1
plays the role of the
image Flask. When multiplying by ∇λ, the first
term of equation (8) produces the reaction in the
PDE (diffusion direction is constraint to be along
the edge). The second term acts as a diffusion (into
the PDE it corresponds to a classical heat equation
in an homogeneous medium). ν is the weight of the
diffusion term. The equation (7) is normalized by
|∇(I
1
)|
2
+2ν
2
.
1)
3)
2)
4)
Figure 3: Diffusion-Reaction with Nagel-Enkelmann Oper-
ator, first and second image represent respectively the flask
and the initial heat value (circle image) images 3 and 4 are
the diffusion-reaction after respectively 2000 and 5000 it-
erations, dt=0.3, total heat i.e sum of pixel’s intensities re-
mains constant.
In this scheme, diffusion will allow to extend the
disparity value in homogeneous regions (and so ex-
press regularity constraint), and the reaction term will
preserve depth contour. To preserve these depth con-
tour, we use the gradient of image I
1
, because a depth
edge implies an image edge. Note that an image edge
does not always correspond to a depth edge (for ex-
ample, the edges of the paving stones on the floor in
the image corridor (see fig. 7)).
Next, we give an attachment term taking into ac-
count the similarity measure, especially for the am-
biguous matches.
4 TWO DIFFERENT
ATTACHMENT TERMS
This section presents our attachment term and how it
deals with ambiguous matches by embedding the dis-
tance to the local minima of a similarity measure. We
present first the similarity measure used by Alvarez.
4.1 Attachment Term of the
Variational Approach
Under lambertian hypothesis the attachment term
used by Alvarez is expressed as the square difference
of grey levels:
|I
1
(x, y) − I
λ
2
(x, y)|
2
(10)
The main inconvenience with this formulation is
that it creates numerous local minima corresponding
to the possible disparities. As a consequence, these
local minima can easily drive the search of the dispar-
ity image toward a false solution. To overcome this
problem the authors have introduced a multi-scale
approach.
Local minima occur frequently in dense disparity
problems, and the similarity measure given by the
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
344

squared difference of intensities is not well-suited
to discriminate which local minima corresponds to
the true disparity. Moreover, even if it is natural in a
classical denoising image algorithm to use difference
of intensity pixels as attachment term, it will be
natural for the disparity map estimation to introduce
a difference of disparity as attachement term.
4.2 A New Attachment Term
Our attachment term is the following:
E
Attach
=
Ω
Disp
min
(x, y, λ)
2
dx dy (11)
where,
Disp
min
(x, y, λ) = argmin
d∈[−V,V ]
(S (I
1
(x, y),I
2
(x, y)
λ+d
))
(12)
with,
• S a similarity measure between the pixel at (x, y)
coordinates from image I
1
and the pixel (x, y)+
h(λ + d)) from image I
2
. S equals 0 if the pixels
are similar and otherwise a positive value .
• V is a ”small” integer constant. For a pixel (x, y) at
the current disparity λ, Disp
min
is the signed dis-
tance which can minimize the similarity measure in
the interval [−V, V ]
Our attachment cannot lead to a gradient strategy
from Euler-Lagrange as in variational method, be-
cause arg min is not a function. To minimize heuris-
tically this energy, we use the iterative process:
dλ
dt
= Cdiv(D(∇I))∇λ + Disp
min
(x, y, λ)
Note that it is classical to lose the variational mean-
ing in regularization PDE techniques such as MCM,
AMSS regularization for example. Anyway, these
PDE have some good interpretations, because they are
defined in the multi-scale frame (Alvarez et al., 1992;
Chambolle, 1994). They correspond to PDE defined
by properties such as isotropy, euclidean invariance,
affine invariance, etc. Due to the use of the arg min,
and because of the violation of comparison principle
(Alvarez et al., 1992), our iterative process is not de-
fined in the multi-scale approach. Nevertheless, we
can define directly some good properties for this It-
erative Scheme to Local Minimum (ISLM). Iterative
processes using arg min have been used for classi-
fication problems (MacQueen, 1967). Here we have
to give at each pixel a value in a class, and it is the
purpose of the arg min. We can define some links
between our problem and a classifying one : the dif-
ferent class for a pixel with our method are the min-
ima of their similarity measure S.
Taking the signed distance to the local minima as
the attachment term gives four principal properties:
• The number of matching candidates is decreased
because local minima of the attachment term of
PDE that are near to each other collapse into one
for ISLM. The position of this minimum corre-
sponds to the one with smallest similarity. A mini-
mum for the d
min
attachment term corresponds to a
minimal similarity S in the neighborhood [−V,V ].
By the way, all local minima m
1
,m
2
, ... for the
similarity measure S, employed by the PDE, with
d(m
i
,m
j
) <V, collapse into one in ISLM. The
position of this minimum is the pixel correspond-
ing to the one with the smallest similarity measure.
Let m
1
be the minimum found by fusion of m
1
and
m
2
. After collapsing, the attraction interval domain
of m
1
will be [m
1
− V,m
1
+ d(m
1
,m
2
)+V ] due
to the absorption of m
2
.
• Our attachment term gives the same weight to all
local remaining minima, and has no effect on ho-
mogeneous areas, so the regularization process can
move the disparity from a local minimum to an-
other one easily by a combinatorial process. This
property is complementary to the first one. For
the pixels whose similarity local minimum is not
defined, i.e we are in a homogeneous region, no
attraction is done. It is clearly the regularization
process that allows to move from an attractor to an-
other one.
• The non ambiguous matches (i.e the ones where
the global minimum score is the true disparity) are
the first disparities found by our process. These
matches restrict, by the regularization constraint,
the research of the ambiguous ones to a subset of
the potential matching candidates. The combinato-
rial nature of this stage gives a propagation process
and is a consequence of the way our attachment
term is evaluated.
• The form of the object is better preserved : we
have observed that the position of the minima on
the boundary of the objects are more stable than the
corresponding values of S along the epipolar line’s
pencil.
The two last properties will be illustrated by exper-
imental data (see 6).
5 IMPLEMENTATION
We use a simple explicit scheme for ISLM:
LOCAL MINIMUM DISTANCE FOR THE DENSE DISPARITY ESTIMATION
345

λ(t)=λ(t − 1)
+ dt ∗ (Cdiv(D(∇I) ∇λ(t − 1))
+ Disp
min
(x, y, λ(t − 1)))
By lack of place, we do not present the explicit
Nagel-Enkelmann discretization operator, see (Al-
varez et al., 2000) for an example of more sophisti-
cated and accurate implementation.
We use as a similarity measure S the square dif-
ference on a correlation mask oriented in the direc-
tion of the epipolar line between the pixel (x, y) and
(x, y)+h(λ). Formula (3) gives the way to compute
the epipolar line, and so the mask direction in image
I
2
with (x, y) coordinates. The mask direction of the
pixel in the image I
1
is found at the same way with
t
F , the transposed fundamental matrix. This classi-
cal result can be found by transposition of the two
terms of the same formula. We present in the exper-
imental section 6, some examples where the 1 × 1
mask (generally we use a 3 × 3 mask). This gives
the same similarity measure used by Alvarez. By the
way, we show the improvements obtained indepen-
dently by the use of the local minimal distance and
our correlation mask similarity measure.
To avoid some local minima produced by the noise
and to give no attraction value for the regions where
score S has small variation, our local distance at-
tachment will be set to zero if the score improve-
ment of the local minimum is less than a threshold.
We smooth the stereo images I
1
and I
2
with a small
gaussian with 0.25 as standard deviation value.
6 EXPERIMENTATIONS
The experimentations present the disparity obtained
on synthetic and real images. We stress the stabil-
ity over all the tests because our method is heuristic
and we have no proof of the convergence. Thanks to
the knowledge of the true expected disparity for our
synthetics images, we present quantitative results and
compare them with other methods. Qualitative results
with disparity obtained from the same stereo couple
from (Alvarez et al., 2000) will be presented for the
real images.
The Quantitative evaluation is computed with the
Error function E:
E(λ
t
)=
Ω−Occult
|λ
t
(x, y) − λ
True
(x, y)| dx dy
Occ is the occulted region not taken into account.
Detection of occulted region can be done by post
0
0.5
1
1.5
2
2.5
3
3.5
50 100 150 200 250 300 350 400 450 500
"EnergieByDispMoins3"
"EnergieByDispMoins6"
"EnergieByImages"
"EnergieByRandom"
Figure 4: E function with different starting from different
disparity images for the iterations between 0 and 500 iter-
ations, correlation disparity, constant disparity and random
map converge to the same disparity map with less than 0.12
pixel error.
processing stage, or embedded in PDE as in (Maier
et al., 2003). As well as (Alvarez et al., 2000;
N.Slesareva et al., 2005) we use a border layer of fif-
teen pixels size.
We use the Corridor stereo scene from:
http://www-dbv.cs.uni-bonn.de/stereo
data/
For this stereo couple of images the true disparity is
available with a very accurate sub-pixel precision.
We have tried our method on several other images
and obtained also very good results.
Our method has been tested with different initial
disparity map. Figure (4) present the evolution of
the error E criteria of ISLM with the number of
iterations. The final disparity image is quite the
same for all the initial disparities. ISLM converge
for a disparity computed by a classical correlation
algorithm, for constant map with disparity fixed at
0, −1, −2, −3,etc. (as it was already done in (Al-
varez et al., 2000)) and more surprising, for random
images with values in [−3, 3] (this experience was
done with different random seeds and several ranges).
For the random initial disparity, first iteratives steps
regularize the value to zero that is the average of the
noise. All the disparities of the squares on the floor
are wrong, the background is the first region where
the disparity is found by our algorithm. After that, the
squares on the floor are found incrementally by dif-
fusion, range by range. The evolution of our iterative
process for random disparity is presented by the first
movie at:
http://www.lgi2p.ema.fr/˜ montesin/Demos/
StereoDense/3d
dense.html
The second movie (same address) shows the itera-
tive process of the evolution of I
1
(x, y + h(λ
t
)) tack-
ing λ
t
0
as the null image. By definition of the dispar-
ity map, I
1
(x, y + h(λ
t
)) must converge to an image
close to I
2
. With a constant and null map as start-
ing point, we can identify clearly the pixel’s moves,
and by the way the dynamic of ISLM. As the random
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
346
C ν E
51.65 0.0375 0.224778
258.29 0.0375 0.119461
464.936394 0.0375 0.128883
51.659601 0.0125 0.226560
TX TY V E
1 1 3 0.133463
3 3 1 0.462112
3 3 5 1.071406
3 3 7 1.762635
5 5 3 0.133292
7 7 3 0.138698
Figure 5: Different values for the specifics parameters for
ISLM. For the first one, the present influence of the variable
issued from the variational parameters C and ν (withTX =
TY = V =3), in the second table we give the influence on
the error E of the specific variables of ISLM TX, TY and
V (with C = 464.936394,Mu=0.037500and dt =0.3).
Methods E
Sub-pixel Correlation method 0.4978
Alvarez (Alvarez et al., 2000) 0.2639
Slesareva (N.Slesareva et al., 2005) 0.1731
ISLM 0.1194
Figure 6: Comparisons with other techniques.
initial value, the pixels in the background are moved
first to the positions of I
2
. These pixels reach at the
beginning their good position because the disparity is
the smallest on this region, the objects in front with
larger disparity move to their I
2
positions at the end.
In the figure (5), the influence of both ISLM para-
meters on the error is presented. Our heuristic con-
verge for a good disparity in most of the cases. TX
and TY are the size of the correlation mask. On this
benchmark, only the parameter of local research V is
important for a good convergence, with V<4 we al-
ways obtain a disparity with sub pixel precision.
Note that with TX = TY =1, the similarity measure
is the one used by Alvarez, and we clearly demon-
strate how our local distance improved the error E in-
dependently of our correlation mask. Table (6) com-
pare the best result obtained with different methods.
The best quantitative result is obtained by our method,
and we present in (7) qualitatives ones. On this im-
ages we can see that the shapes of the cone and the
sphere are better preserved by ISLM.
Experiments for detection of the noise influence
(with noisy images available on the same internet ad-
dress) give results that we compare with those from
(N.Slesareva et al., 2005) on figure (8). Here again
our quantitative results are better, and the higher the
error value is, the more significant the improvement
is (see Column Ratio).
We use now the real images from the INRIA avail-
able at
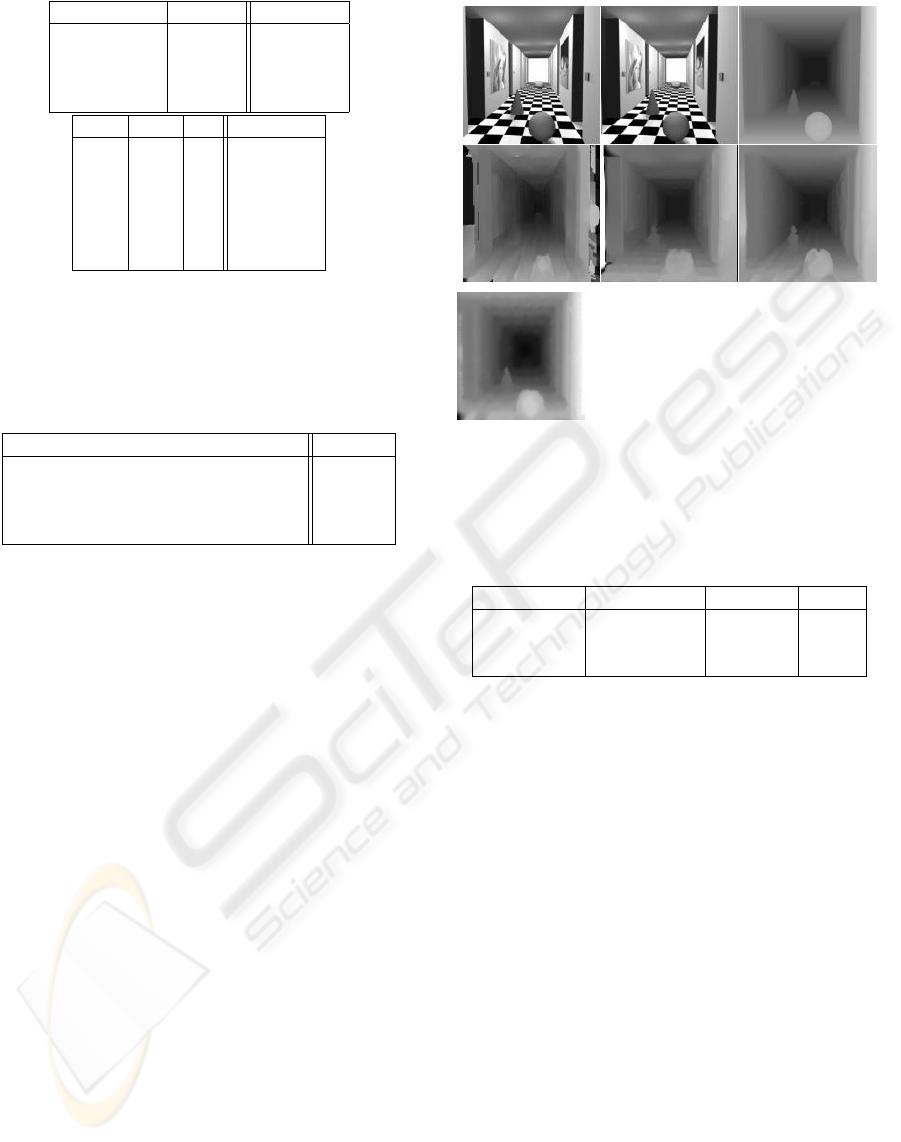
Figure 7: From the left to the right and from the top to
the bottom, the stereo couple, the true disparity, the dispar-
ity from correlation algorithm, PDE from Alvarez (Alvarez
et al., 2000), method from Slesareva (N.Slesareva et al.,
2005), and finally our method. Note that the form of the
cone and the sphere are better preserved.
Noise level E Slesareva E ISLM Ratio
001 0.1952 0.1745 1.118
010 0.2529 0.2172 1.160
100 0.3297 0.26720 1.233
Figure 8: Comparison with methods from (N.Slesareva
et al., 2005) on noisy images, C =21.9215, ν =0.375,
TX = TY = V =3dt =0.3. Ratio gives E from
Slesareva divided by E from ISLM.
http://www-sop.inria.fr/robotvis/demo.
We present the three dimensions reconstruction.
ISLM convergence is more time consuming than
the other algorithms, with initial disparity found by
classical correlation algorithm it takes 6 minutes and
14 seconds to avoid 0.17 pixels precision, and 26
minutes 47 seconds to converge to 0.12 with a Pen-
tium 4). Due to our attachment term, we can not deal
with less time consuming implementation as an im-
plicit scheme. So our method seems not to be de-
signed for real time process as software but by hard-
ware and parallel implementation.
7 CONCLUSION
In this paper we have presented an iterative algorithm
for the stereo dense disparity estimation principally
based on a new attachment term. In order to give more
consistent value to the similarity measure of our itera-
LOCAL MINIMUM DISTANCE FOR THE DENSE DISPARITY ESTIMATION
347

Figure 9: Two views on Herve face, and a view on the 3D
reconstruction, ν =0.0625, C =21.75 TX = TY =7
V =3.
tive process, we use a correlation mask oriented along
the epipolar line. Then instead of taking a similarity
value as attachment term we use the distance to local
minimum obtained by the similarity. Consequently
our iterative scheme is no more linked to an energy
minimization but presents some characteristics of a
relaxation process embedding in the same framework
continuous and combinatorial aspects. The experi-
mentations show that our method convergences and
produces the best known quantitative results on im-
age benchmarks presenting continuous aspects in di-
parity values. Now we are trying our method on mid-
dlebury benchmarks. These benchmarks are different
from corridor scene because first the disparity image
contains a lot of disparity steps, and second that the
disparities available in the middlebury benchs have
discrete values. As our algorithm gives a continuous
range of values, the error is difficult to clearly inter-
pret. Links to other studies can be done, leading us to
expect again new improvements simply by the use of
other similarity measures. For example, the similar-
ity measure from (N.Slesareva et al., 2005), or (Takeo
and Okutomi, 1994) can be used in our attachment
term.
REFERENCES
Alvarez, L., Deriche, R., Sanchez, J., and Weickert, J.
(2000). Dense disparity map estimation respecting
image discontinuities: a pde and scalespace based ap-
proach.
Alvarez, L., F., G., P.L., L., and J.M., M. (1992). Ax-
ioms and fundamental equation of image process-
ing. Technical Report 9231, CEREMADE, Universit
´
e
Paris Dauphine, France, Mars 1992. Paru dans Arch.
for Rat. Mechanics 123(3), pp 199-257, 1993.
Blomgren, P. (1998). Total Variation Methods for Restora-
tion of Vector Valued Images. PhD thesis, University
of California, Los Angeles.
Boufama and Jin (2002). Towards a fast and reliable dense
matching algorithm.
Chambolle, A. (1994). Partial differential equation and
image processing. IEE Int. Conf. Image Processing,
Austin, I:16–20.
Gouet, V., Montesinos, P., and Pel
´
e, D. (1998). Stereo
matching of color images using differential invari-
ants. In International Conference on Image Process-
ing, Chicago, USA.
MacQueen, J. (1967). Some methods of classification and
analysis of multivaluate observation.
Maier, D., Role, A., Hesser, J., and Manner, R. (2003).
Dense disparity maps respecting occlusions and ob-
ject separation.
Nagel, H. (1983). Constraints for the estimation of deplace-
ment vector fields from image sequences. IJCAI.
N.Slesareva, A.Bruhn, and J.Weickert (2005). Optic flow
goes stereo: A variational method for estimating
discontinuity-preserving dense disparity maps.
Ohta, Y. and Kanade, T. (1985). Stereo by intra- and inter-
scanline search using dynamic programming.
Scharstein, D., Szeliski, R., and Zabih, R. (2001). A taxon-
omy and evaluation of dense two-frame stereo corre-
spondence algorithms.
Takeo, K. and Okutomi, M. (1994). A stereo matching al-
gorithm with an adaptative window : theory and ex-
periment.
Torr, P. and Murray, D. (1997). ”the development and com-
parison of robust methods for estimating the funda-
mental matrix”. International Journal of Computer
Vision, 24(3):271–300.
Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q. (1994).
”a robust technique for matching two uncalibrated
images through the recovery of the unknown epipo-
lar geometry”. Technical Report RR-2273, INRIA
Sophia-Antipolis, France.
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
348
