A NEW TECHNIQUE FOR COLOR IMAGE QUANTIZATION

Wafae Sabbar, Abdelkrim Bekkhoucha

University Hassan II Mohammedia, FST Mohammedia, Computer sciences department

BP 146 Mohammedia 20650 Morocco

Keywords: Colour image quantization; Multi-thresholding; Highpass filtering, Lowpass filtering.

Abstract: In this paper, we introduce a new technique of color image quantization. It is carried out in two processing.

In the first, we decrease the number of color using a multi-thresholding, by intervals, of the three marginal

histograms of the image. In the second processing, the colors determined in the first processing are reduced

by colors fusion based on the mean square error minimization. The algorithm is simple to implement and

produces a high quality results.

1 INTRODUCTION

Color image quantization is an important problem in

computer graphics and image processing, it is a very

useful tool for segmentation, compression,

presentation and transmission of images. It’s defined

as an irreversible image compression technique. The

main objective is to map the full color in the original

image to a much smaller palette of colors in the

quantized image by introducing a minimal distortion

between the two images (Xiang, 1994). It is very

difficult to formulate a definite solution to the image

quantization problem in terms perceived image

quality.

Mathematically, color image quantization can be

formulated as an optimization problem:

Let C={c

, i=1,2...N} be the set of all colors in the

image I, c

is a vector in one of the color spaces

(Lu*v*, HSV, RGB, ect.). A quantized image I

represented by a set of K colors C

={c

, i=1,2..K},

K<<N. The quantization process is therefore a

mapping:

q: C

(1)

The closet neighbor principle states that each color c

of the original image I is going to be mapped into

the closet color c’ from the colour palette C

')( ccq =

-min

...2,1

= (2)

The quantization mapping defines a set of cluster

k/k=1,2..K

in the image color space C

{}

ccqCcS =∈= )(: (3)

Color image quantization has been widely

studied for the last fifteen year, the existing

techniques of quantization can be divided into three

categories (Sangwine, 1998):

Pre-clustering algorithm: Most of the proposed

algorithms are based on statistical analysis of the

color distribution of image pixels within the color

space. The Popularity et Median Cut (Heckbert,

1982), Variance Minimization (Wan, 1990), Octree

(Gervautz, 1990) and Principal Analysis Algorithm

(Wu, 1992) are examples of this scheme.

Post-clustering algorithm: It involves an initial

selection of a palette followed by iterative

refinement of this palette using the K-Means

algorithm (Linde, 1980) to minimize the Mean

Square Error. Fuzzy C-mean (Lim, 1990) is an

extension of the K-means algorithm. The Hierarchy

Competitive Learning (HCL) (Scheunders, 1997)

and Neuuant (Dekker, 1994), exploiting the

Kohonen Self-Organizing-Maps (Kohonen, 1989]

are examples of this scheme.

Mixed algorithm: there exists a different algorithm,

which combines between the two approaches

precedent, for example the algorithm Split-Merge

described by Brun (Brun, 2000).

In this work, we propose a new method of color

image quantization witch use a multi-thresholding

followed by a merge step. The next sections are

organized as follows: In section 2 we describe the

multi-thresholding method of a marginal histogram.

In section 3 we describe our method. Experimental

results are presented in section 4. Conclusions

appear in section 5.

147

Sabbar W. and Bekkhoucha A. (2006).

A NEW TECHNIQUE FOR COLOR IMAGE QUANTIZATION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 147-150

DOI: 10.5220/0001370101470150

 SciTePress

2 MULTI-THRESHOLDING

METHOD OF A HISTOGRAM

The objective of multi-thresholding is to devise the

histogram into a desired number of classes, every

class is represented by a peak (maximum) and

constituted by all values between two valleys

(minimum). We first evaluate the number of peaks

in the histogram, if the number of peak is more than

the desired one, we must attenuate the high-

frequency components and decrease the number of

peak by Gaussian filtering (lowpass filtering).

Otherwise, we attenuate the low-frequency

components and increase the number of peaks by

highpass filtering when the number of peaks in the

histogram is less than the desired one (Chang, 1997).

2.1 Lowpass filtering

Given a marginal histogram h(x) of an image, the

lowpass filtered L(x,

) of h(x) can be obtained using

the convolution of h(x) with a Gaussian function

g(x,

∫

−

⎥

⎦

⎤

⎢

⎣

⎡

hxL

πσ

μσ

)-(

exp

)(),(

(4)

Where

denotes de spread parameter of g and

is a

dummy variable. Local maxima (peaks) and minima

(valley) of h(x) can be found from the first partial

derivate L

(x,

) of L(x,

). The peaks of L(x,

) are

zero crossings in L

(x,

) whose signs change from

plus to minus. However, valleys of L(x,

) are zero

crossing in L

(x,

) whose signs change from minus

to plus.

Let P(

) denote the number of peaks in the

filtered histogram, P(

) is function of the spread

parameter

and decrease monotonically while

increase, we must find a good

to obtain the desired

number N

class

of class (peak). In order to resolving

the problem, we apply a Dichotomy method, when

the search stops, we obtained an interval of

approached value. Let

σ∗

be the upper bound of the

interval, we have two case: If P(

σ∗

)=N

class

we stop

research. If P(

σ∗

)>N

class

, we must merge P(x,

σ∗

class

peak that gives a weak variance

2.2 Highpass filtering

When the histogram has a smaller number of peaks

than the desired number of classes, we apply a

highpass filtering. The highpass used here is

)

.2-

exp(),(

sxh =

(5)

Where the parameter s determines the bandwidth of

the stop band in the highpass filter. The highpass

filtered histogram H(x,s) of h(x) can be easily

computed in the frequency domain. We first use a

discrete Fourier Transform (DFT) to transform the

histogram h(x) to frequency domain and then apply

the highpass filter to attenuate its low frequency

components. Finally, the inverse Discrete Fourier

Transform (IDFT) is used to obtain the highpass

filtered histogram

3 QUANTIZATION METHOD

WITH THE MULTI-

THRESHOLDING BY

INTERVAL

Our method first uses a multi-thresholding, by

intervals, of the three marginal histograms h

red

, h

green

and h

blue

of the image. In the second processing, the

colors determined in the first step are reduced by

colors fusion based on the mean square error

minimization.

3.1 Multi-thresholding by interval

Each marginal histogram h

red

, h

green

and h

blue

image can be cut out in several intervals presented

by modes. The number of thresholds to be

determined in each interval must be proportional to

the quantity of information of this one.

We evaluates the number of peaks in each interval,

if the number of peak is more than the desired one,

we decrease the number of peak by lowpass

filtering. Otherwise, we increase the number of

peaks by highpass filtering when the number of

peaks in the interval is less than the desired one

3.2 Fusion of colour

Let C={c

, c

,..c

} the N produced colour by the first

processing, so we have N cluster P={C

,....C

}. If K

is the required number to quantify our image, we

must merging N-K cluster in N-K iteration. The

merge of two cluster C

and C

create a new partition

P’ with a square error E(P’) (Brun,2000).:

CμCμ

PEPE

)(-)(

+)(=)'(

(6)

VISAPP 2006 - IMAGE FORMATION AND PROCESSING

148

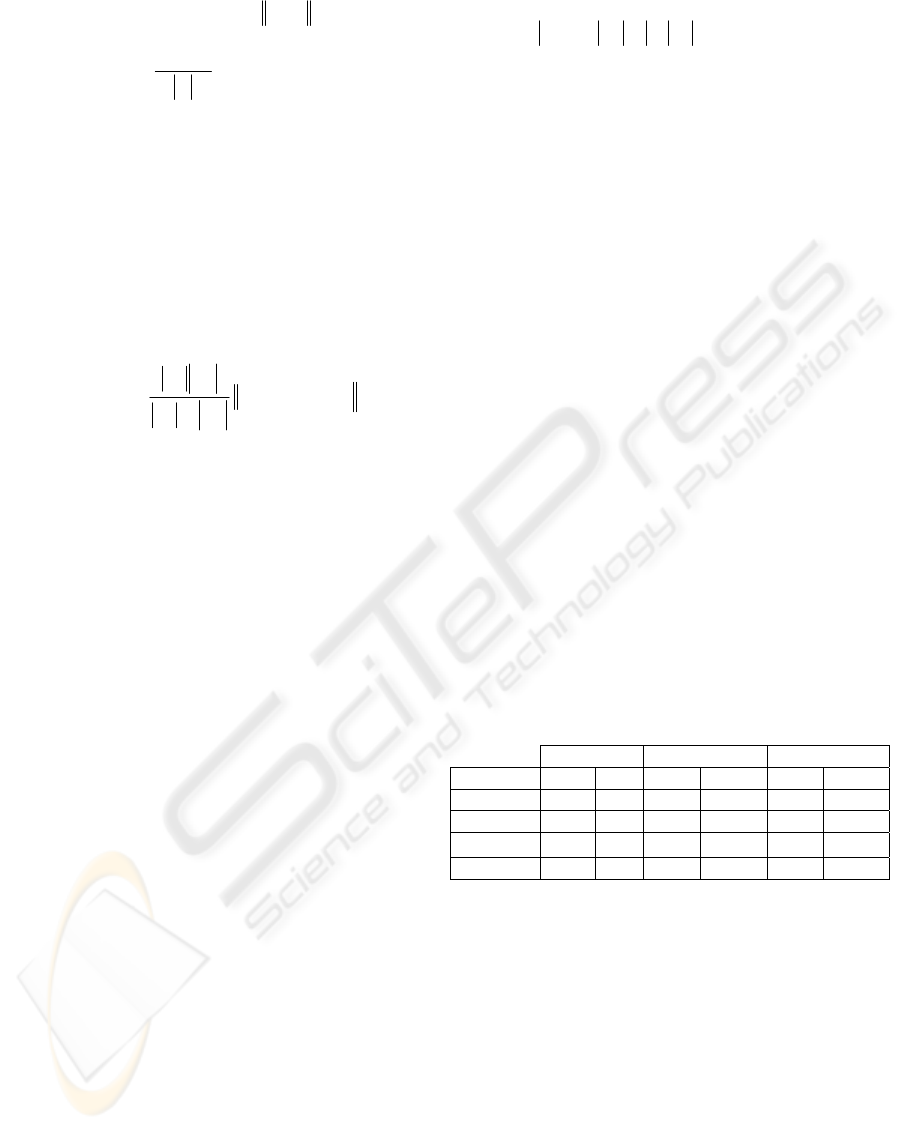
where

∑∑

=∈

i imagec

cccfPE

-)()( (7)

and

)(

∑

∈

ccfCM ).()(

(8)

f(c) is the number of pixels with color c in the image

and

μ(

)

is the means color for the cluster C.

Our merger create a graph called the Cluster

Adjacency Graph “CAG” (Brun,2000). The “CAG”

is mesh-like and has few edges that cross over each

other. Furthermore, the variance in the length of the

edges between adjacent nodes is small.

The nodes of our graph are the cluster to be

merged and each edge shared by two nodes n

and n

respectively associated to the cluster C

and C

valuated by

Δ(

i,j

)

)(-)(),(

μμ

=Δ

(9)

If we encode the “CAG” by an half-matrix G, the

two nodes n

and n

which have be merged are

defined by:

{}{ }

]][[),(

1,...,1,...,1),(21

jiGArgMinnn

iNji ×∈

= (10)

),(]][[ jijiG

= (11)

In order to improve the search of the nodes which

have to be merged, we use an array Min defined by:

{}

]][[][,......,1

1,...,1

jiGArgMiniMinNi

ij −∈

∈∀

The two merged nodes (n

) are then defined by:

{}

⎩

⎨

⎧

∈

][

]][][[

,....11

nMinn

iMiniGArgMinn

(13)

Using the array Min, the computation of nodes n

and n

is performed with O(N) tests.

If we invalidate nodes n

, the update of this half

matrix requires to invalidate line and column n

and

to update line and column n

. The invalidation of

lines and column n

being performed in constant

time, this last point requires O(N) operations.

Moreover, we also have to update the value Min[i] if

Min[j] is equal to n

or if the update of line and

column n

has changed the minimum value have of

one line. In the best case where no update occurs, we

have to perform O(N-n

-1) tests. In the worst case,

all values Min[i] for i greater than n

have to be

updated. In this last case, the update of the array Min

require O(

∑

−

1 ) operations.

The merger needs at each node the centroid and the

cardinal of the corresponding clusters. By using

equation (8), the mean can deduced from the first

cumulative moment M

and the cardinal. Moreover,

as all cluster are disjoints, the first moment and the

cardinal are linear operators:

⎩

⎨

⎧

+=∪

2121

2111211

)()()(

CCCC

CMCMCCM

(14)

As the mean can be deduced from the first moment

and the cardinal, we only store these two data in

each cluster.

4 EXPERIMENTS

In order to illustrate the results of our proposed

quantization method, we choose different images

tests very widely used in the domain of the image

processing: “Lena”(Figure 1), ”Mandrill” (Figure 2)

and “Monarch” (Figure 3), its coded in 24 bit. We

compare the new method with popular quantization

algorithm found in public domain image processing

software: Median cut, Octree and SM (Split and

Merge).These implementation worked in RGB

colors space for a fair comparison, we also use the

RGB space. The table 1 shows the distortions

produced by the quantization methods with 16 and

256 output colors. We remark that our method give

the lowest distortion for different images, the

difference is great for a quantization with 16 output

colors. Small values of distortion guarantee that a

quantization process accurately represents colors of

the original image. We notice also that the image

loses its quality from a quantization in 16 colours or

inferior.

Table1:.The distortions produced by our algorithm, SM,

Median cut and Octree.

Lena Mandrill Monarch

Nb of color

16 256 16 256 16 256

S.M

27.58 8.21 31.53 9.69 25.88 9.50

Median cut

24.65 8.23 29.54 10.55 24.67 8.66

Octree

28.08 9.46 33.02 11.50 25.58 10.58

Our meth

19.06 6.99 25.10 9.06 23.02 8.16

5 CONCLUSION

In this work we have developed a new method for

color image quantization in two processing: we use a

multi-thresholding, by intervals, of the three

marginal histograms of image in the space of color

RGB to reduce and recover the interesting color. In

order to find the required number of colors to

quantize the image, we merge the colors given a

minimal means square error using a “CAG”. The

method is simple, efficient and gives good results on

various test images.

A NEW TECHNIQUE FOR COLOR IMAGE QUANTIZATION

149

REFERENCES

Heckbert, P., 1982. Color image quantization for

frame buffer displays. Computer Graphics,

Vol.16, No. 3, 297–307.

Xiang, Z., Joy G., 1994. Color image quantization

by agglomerative clustering. IEEE Computer

Graphics and Applications, 14(3): 44-48.

Xiofan, Wu., 1992. Color quantization by dynamic

programming and principal analysis. ACM

Transactions on graphics, 11(4) : 348-

372,Octobre.

Sangwine, S. and R. Horne, 1998,The Colour Image

Processing Handbook, Chapman & Hall.

Wan, S. J., Prusinkiewicz, P., and Wong, S.K.M.;

1990. Variance-based color image quantization

for frame buffer display. Color Research and

Application, Vol. 15, No. 1, 52-58.

Gervautz, M., Purgathofer, W., 1992. A simple

method for color quantization: Octree

quantization. Graphic Gems, Academic Press,

New York (1990) 287–293.

Wu, X., 1992. Color Quantization by Dynamic

Programming and Principal Analysis. ACM

Transactions on Graphics, Vol. 11, No. 4, 348-

372.

Linde, Y., Buzo, A., Gray, R., 1980. An algorithm

for vector quantizer design. IEEE Transactions

on Communications, Vol. 28, No. 1, 84–95.

Lim,Y.W., Lee, S.U., 1990. On the color image

segmentation algorithm based on the

thresholding and the fuzzy c-means techniques.

Pattern Recognition, Vol. 23, 935-952.

Scheunders, P., 1997. A comparison of clustering

algorithms applied to color image quantization.

Pattern Recognition Letters, Vol. 18, 1379-1384.

Kohonen, T., 1989. Self-Organization and

Associative Memory, Springer-Verlag, Berlin.

Dekker, A., Kohonen, 1994. neural networks for

optimal colour quantization, Network.

Computation in Neural Systems, Vol. 5,351–367.

Brun, L., Mokhtari, M., 2000. Two high color

quantization algorithm. CGIP’2000, Saint

Etienne.

Chang, C. C., Wang, L.L., 1997. A fast multi-

thresholding method based on lowpass and

highpass filtering. Pattern recognition Letters,

181469-1478.

Figure 1: (the left in right) Image lenna original, image

uantized in 256

128

16 colours.

Figure 2: (the left in right) Image Mandrill original,

ima

antized in 256

128

16 colours.

Figure 3: (the left in right) Image Monarch original,

ima

uantized in 256

128

16 colors.

VISAPP 2006 - IMAGE FORMATION AND PROCESSING

150