SIMPLIFIED REPRESENTATION OF LARGE RANGE DATASET

Hongchuan Yu and Mohammed Bennamoun

School of Ccomputer Science & Software Engineering

University of Western Australia,WA 6009,Australia

Keywords: Range Dataset, Simplification, SVDecomposition, Radial Basis Functions.

Abstract: In this paper, we consider two approaches of simplifying medium- and large-sized range datasets to a

compact data point set, based on the Radial Basis Functions (RBF) approximation. The first algorithm uses

a Pseudo-Inverse Approach for the case of given basis functions, and the second one uses an SVD-Based

Approach for the case of unknown basis functions. The novelty of this paper consists in a novel partition-

based SVD algorithm for a symmetric square matrix, which can effectively reduce the dimension of a

matrix in a given partition case. Furthermore, this algorithm is combined with a standard clustering

algorithm to form our SVD-Based Approach, which can then seek an appropriate partition automatically for

dataset simplification. Experimental results indicate that the presented Pseudo-Inverse Approach requires a

uniform sampled control point set, and can obtain an optimal least square solution in the given control point

set case. While in the unknown control point case, the presented SVD-Based Approach can seek an

appropriate control point set automatically, and the resulting surface preserves more of the essential details

and is prone to less distortions.

1 INTRODUCTION

A range dataset is a picture in which each pixel

value encodes not the intensity of a usual 2D image

but rather the depth (or range) information. This type

of imagery therefore provides direct, explicit

geometric information which is useful in many

applications. However, this range dataset is usually

large-sized, non-uniformly sampled (i.e. the surface

is typically irregularly sampled, and exhibits varying

sampling densities), and contains noise or unwanted

details. The challenging problems include the

interpolation of the scattered surface dataset, the

removal of the inherent noise from the range dataset

and the simplification of this dataset for the large-

sized case. At present, the Radial Basis Functions

(RBF) are popular for interpolating scattered data

since they can effectively interpolate across large,

irregular holes in incomplete surface data without

constraining the topology of an object or any priori

knowledge of the shape (Carr et al. 2003, 2001,

1997, Morse et al. 2001). (Carr et al. 2003), further

employed RBF technique to smooth the scattered

range data. As an alternative approach, (Fleishman

et al. 2005), recently employed the Moving Least-

Squares (MLS) technique to handle noisy range

datasets. However, since these range dataset usually

contains a large data point set, this will bring about a

higher computational complexity. For example,

computing a RBF interpolation is performed by

solving an associated linear system of basis

functions of size up to (N+K)×(N+K), where N is the

number of control points and K is the number of a

low polynomial coefficients. As this system

becomes larger, the amount of computation required

to solve it grows as

)(

NO . In order to decrease the

computational complexity, (Beatson et al. 1999,

2001, 2000) and (Suter 1994) proposed their

individual fast evaluation approaches that have a

complexity of O(NlogN).

However, the range dataset usually contains

redundant information to represent a surface.

Considering all the points as control points to fit the

surface must lead to a higher complexity, and this is

indeed unnecessary. But how to simplify the range

dataset is still an open problem. This paper deals

with the problem of range dataset simplification, and

aims at the simplification of the RBF approximation.

To the best of our knowledge, this problem has only

been addressed by (Carr, et al. 2001), who proposed

a greedy algorithm for reducing the data point set.

Their basis idea is to use the fitting accuracy as the

criterion to choose the control points. In our works,

we prefer to pay attention to the space distribution of

the point set, since its inherent geometric properties

indicate which points are critical to represent a

172

Yu H. and Bennamoun M. (2006).

SIMPLIFIED REPRESENTATION OF LARGE RANGE DATASET.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 172-179

DOI: 10.5220/0001374201720179

 SciTePress

surface. The main contribution of this paper is to

present a novel partition-based SVD approach,

which can be employed to reduce the dimension of a

large-sized symmetric square matrix. Furthermore,

we employed this novel tool to the range dataset

simplification, and the resulting surface preserves

more essential structures and less distortion.

The remainder of this paper is organized as

follows. In Section 2, the RBF approach is first

introduced briefly. Then, we introduce two approach

of simplifying the RBF approximation in Section 3,

one is the Pseudo-Inverse Approach and other is the

SVD-Based Approach. Experiments and analysis are

shown in Section 4. Finally, Section 5 gives our

conclusions and future works.

2 RADIAL BASIS FUNCTIONS

An implicit surface is defined by an implicit

function, which is a continuous scalar-valued

function over the domain, i.e.

RRf

→: . Therein,

the function values of points at the implicit surface

take on zero, while the function value takes on

positive value interior to the implicit surface and is

negative outside the surface (or conversely). The

magnitude is defined as the distance from a point to

the implicit surface. This implicit function is also

called a signed distance function. Our goal is to

recover the implicit function f from a set of dataset

(or control point set). Indeed, this is an ill-posed

problem, since it has an infinite number of solutions.

The standard procedure is to obtain a solution of this

ill-posed problem from a variational principle, that

is, to minimize the following functional,

()

∑

′

−

fff

][)(min

αφ

x , (1)

where,

R∈x is control point coordinate vector,

′

is the function value of

x ,

[f] is a smoothness

functional (in general, the thin-plate energy

functional (Carr et al. 2001) is adopted), and α is the

regularization parameter.

An effective expression of the solution of Eq.(1) is

in terms of radial basis functions centered at the

control points. Radial basis functions are radially

symmetric about the control points, which is written

as follows,

∑∑

+−=

dGcf

)()()( xxxx

, (2)

where,

)(

xxG − is a basis function

RRRG

→×: ,

}{

is a basis in the K-

dimensional null space. In order to determine the

coefficients

c and

d , one can solve the following

linear system.

⎟

⎠

⎞

⎜

⎝

⎛

′

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

, (3)

where,

ff ),...,(

′′

′

, )(

jiij

GG xx

−

= ,

cc ),...,(

=c ,

dd ),...,(

=d . The basis function

is of the form

)||(||)(

⋅

GG , which includes

biharmonic spline, triharmonic spline and

multiquadric (refer to (Carr et al. 2001) for details).

The

∑

d )(x

in Eq.(2) is usually a degree one

polynomial since the thin-plate energy consist of

second order derivatives.

In the scattered data interpolation case, it is

straightforward to employ all the data points to

construct the coefficient matrix of Eq.(3) and

directly solve the coefficient vectors c and d. Herein,

all the data points are regarded as control points. For

the small-sized range datasets, this direct approach is

very useful for the direct solution of the

interpolation problem. But in the moderate- and

large-sized cases, the coefficient matrix of Eq.(3)

would exceed the computational capability of the

usual machine. Thus, the control point set has to be a

subset of the whole range dataset. Indeed, the range

dataset is usually redundant with respect to the

representation of a surface. It is unnecessary to

regard all the data points as control points.

3 SIMPLIFICATION OF RANGE

DATA

Consider the medium- and large-sized range datasets

case. In this section, we devise two approaches in

order for the solution of the implicit function f to

account for the control point set and non-control

point set.

3.1 Pseudo-Inverse Approach

In this case, the control point set is known in

advance. This means that the basis functions have

been determined and the basis of the functional

space of the implicit function f are fixed. Herein, we

only need to select an appropriate set of coefficients

c and

d for Eq.(2). This can be achieved through

minimizing the following functional,

SIMPLIFIED REPRESENTATION OF LARGE RANGE DATASET

173

⎟

⎠

⎞

⎜

⎝

⎛

′

−+

′

−

∑∑

ffff

),,(

),,(),,(min dcxdcx

dcx

, (4)

where, N is number of control points, M is number

of non-control points.

Considering Eq.(2), Eq.(3) and Eq.(4) together, one

can convert the above minimization problem as

follows,

⎟

⎠

⎞

⎜

⎝

⎛

′

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

(5)

where,

′

and

′

are respectively the vectors of

function values of control points

x and non-control

points

x ,

G and

are constructed by the

control points, which are described in the same

manner as in Eq.(3),

G and

are constructed by

the non-control points, which can simply be

determined using Eq.(2) with the same control

points that are used for

G .

G is a symmetric

matrix of size N×N while

G is a asymmetric

matrix of size M×M. Through the pseudo-inverse of

the coefficient matrix in Eq.(5), we can obtain a

solution of

c and d in a least square sense.

The advantages of this approach are several. First,

the algorithm is easily implemented since only the

linear system of Eq.(5) needs to be solved. Second,

the error converges since we can get a least square

solution from Eq.(5). However, its deficiencies are

also obvious. From a theoretical viewpoint, the

control point set is redundant. As we knew, the basis

functions

)(

G xx − were non-compactly supported.

This means that the control point set is redundant

with respect to the representation of a surface.

Furthermore, because the control points are fixed,

the resulting implicit function of Eq.(2) is bounded

in the functional space spanned by the basis function

)(

G xx − . It is impossible to deform the implicit

function f to go beyond this original functional

space. This means that the control points should be

uniform samples over the whole domain but not the

local samples. Therefore, it is necessary to

investigate the choice of the control points. From the

perspective of an application, in large-sized range

data case, due to a large number of data points, the

coefficient matrix of Eq.(5) would quickly exceed

the computational capability of the usual machine.

In the following section, we will try to devise a

novel approach to overcome these two problems.

3.2 SVD-Based Approach

In this case, the control point set is unknown. Our

basic idea is to apply the Singular Value

Decomposition (SVD) to the coordinate set of range

data points to simplify the data points so as to obtain

some principal control points. Obviously, the first

problem we encountered will be the conflict between

the large-sized point coordinate set and the usual

limited computational capability. It is

straightforward to partition the large-sized set into a

series of subsets, and then deal with them

individually. In the following, we first explain our

novel partition-based SVD approach, then apply it to

the large-sized data point set for point simplification.

In the RBF approximation, the coefficient matrix of

Eq.(3) is real symmetric and positive semi-definite.

Our goal is to exploit these properties in order to

reduce the dimension of this square matrix. Without

loss of generality, we first give the following two

basic propositions (see (Yu et al. 2005) for a formal

proof).

Proposition 1

Let a real symmetric matrix

∈A be SVD

decomposed as

VUA Λ= , where

0...),,...,(

≥≥≥

diag

. If r≤rank(A)

and let

VUA

′

′′

′

, where

rrrn

××

∈Λ

′

∈

′′

,,VU

, then,

′

−

AA .

Proposition 2

Partitioning columns of A into r block submatrices

),...,(

1 r

AAA

, where riR

,...,1, =∈

A ,

∑

, we have, )()(

rankrank AAA = .

Proposition 1 implies that

′

is an optimal

approximation of A among all rank r matrices in a 2-

norm sense. Furthermore, if rank(A)=r and r<n, this

implies that A can be partitioned into r block

submatrices and each block submatrix is expected to

be of rank 1.

Due to the real symmetry property of A, each block

partitioned along column (or row) must correspond

to a block partitioned along row (or column). For

convenience, each strip block can be compressed to

a real symmetric matrix. Proposition 2 implies that

this compressed symmetric matrix

AA has the

same rank as

A . Therefore, we are able to expect

VISAPP 2006 - IMAGE UNDERSTANDING

174

the square matrix

AA to be of rank 1. This

procedure is illustrated in Fig.1.

⎟

⎠

⎞

⎜

⎝

⎛

=→

⎟

⎠

⎞

⎜

⎝

⎛

AAA

*...*...*

***

*...*...*

111





Figure 1:Real symmetric matrix A is converted to a quasi-

diagonal form B.

It can be noted that the compressed matrices

construct a block diagonal matrix B. In other words,

the partition of A is transformed to a block diagonal

matrix B. This transform effectively simplifies the

computation burden, since the future numerical

analysis of A can be fulfilled through the individual

analysis of each symmetric block

AAB = .

Applying SVD decomposition to

B , one can get

iiii

VVAAB

Λ== , where the SVD of

A is

iiii

VUA Λ=

. When we let

1)()( ==

rankrank AAB , the approximation of

B can therefore be written as,

iii

)(

vvB

′

where

)(

is the maximum singular value of

Λ ,

)(

is the column singular vector of

corresponding to

)(

. Consequently, B can be

reconstructed by the approximations

′

,...,

follows,

(

)

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

′

diag

)(

)1(

)(

)1(

)(

)1(

,...,





λλ

(6)

For each block

B , we know that

B is indeed the

Gram matrix of

A , which is symmetric and

positive definite. The diagonal difference between

B and its approximation

′

indicates which

column (or row) vectors of

A are principal basis

vectors of

A . This is due to the fact that each

diagonal entry of

B is the inner product of each

column (or row) vector of

A . If the ith column (or

row) vector is a principal vector of

A , its inner

product can be approximated by the ith diagonal

entry of the approximation

′

. One can

conveniently preserve a column (or row) of

A by

evaluating

jji

pjbbbb ,...,1,,,

)(

′

∈

′

∈

′

− BB so that

these selected columns (or rows) construct an r-

dimensional matrix

rr×

, which is a dimension

reduced version of A.

Up to now, we established a partition-based SVD

approach for the large-sized real symmetric matrix

case. It can be summarized as follows.

Partition-Based SVD Approach:

Convert the partitioned

()

AAA ,...,

= to

a block diagonal matrix B;

Compute the approximation

′

of each

symmetric subblock

B in B through SVD,

in which

(

)

′

rank B ;

Compute the diagonal difference between

B and

′

;

Select the principal vector of

A by

evaluating

jji

bbbb BB

′

∈

′

∈

′

−

)(

,, to

construct the reduced matrix

of size r×r.

However, it can be noted that the approximation

error of B can be evaluated through 2-norm of

′

−

. Moreover, the upper bound of error can be

estimated as

)(

max

≤

′

− BB (for details, refer

to [10]). Indeed, a good partition approach can be

deduced by minimizing the error of

)(

max

. It can

also be noted that

)(

max

is a variable for various

partition approaches. It can be further proven that for

the singular values of each column of A,

,...,

and

0...

≥≥≥

, there exists a partition (i.e. the

dimension of A is reduced to r) such that,

2)...(max

)(

2 nrr

σσσλ

+++≤

(for details, refer

to (Yu et al. 2005)). This implies that

),...,,(

1 nrr

correspond to the non-principal

columns (or rows) of A respectively, and in order to

further reduce the error of

)(

max

, we have to

seek a column (or row) combination of A (i.e. all the

non-principal columns or rows are left in

A ) so as

to obtain the minimum of

()

...

nrr

σσσ

+++

. Of

course, if the non-principal columns or rows are

distributed in each partition

A , this minimization

problem will be described as follows,

SIMPLIFIED REPRESENTATION OF LARGE RANGE DATASET

175

(

)

)(

...max min

σσ

++ .

However, seeking the optimal partition of A is

indeed an NP-complete problem. We will present

below our partition scheme in the case of range data

simplification.

Consider a coordinate set of range data points. One

can note that the distribution of the point cloud

formed by data points is not uniform. The geometric

distribution of data points is redundant with respect

to the topological structure of a point cloud. In order

to obtain a compact data point set, we can directly

apply the SVD technique to the basis functions of

Eq.(3). Indeed, the sub-matrix G in Eq.(3) consists

of the basis functions

)(

G xx − , which is a real

symmetric and positive semi-definite matrix. If there

existed a partition for G, applying the above

presented partition-based SVD approach to G, one

could easily simplify G to get a dimension reduced

version of G. But, how to partition G is still an open

problem that is covered in this section.

Considering G, one can note that the basis function

)(

G xx − is a function of the Euclidean distance

xx − , and )()(

ijji

GG xxxx −

− . The ith row

(or column) of G is a vector of

()

)(),...,(

1 iNi

GG xxxx −− about the ith point

x .

Herein, the geometric meaning of the singular values

of the columns (or rows) of G is that the singular

value

of column (or row) i of G is a

measurement of the divergence of the data point set

to the ith data point

x , i.e. the bigger the singular

value

is, the farther the data point set departs

from the ith data point

x . In terms of proposition 2,

the r columns (or rows) of G with the first r

maximum singular values of columns should be put

into r different partitions of G. It is clear that the

resulting partition of G through the selection of

points with the larger divergence as the centers of

the different partitions can minimize the residual

error between G and its approximation

′

However in our case, G is not approximated by the

same dimension of

′

but its dimension is reduced

(i.e. the number of control points needs to be

reduced). Obviously, the reduction of the control

points will lead to the loss of some details. If only

the points with the largest divergence are

considered, many details will have to be abandoned.

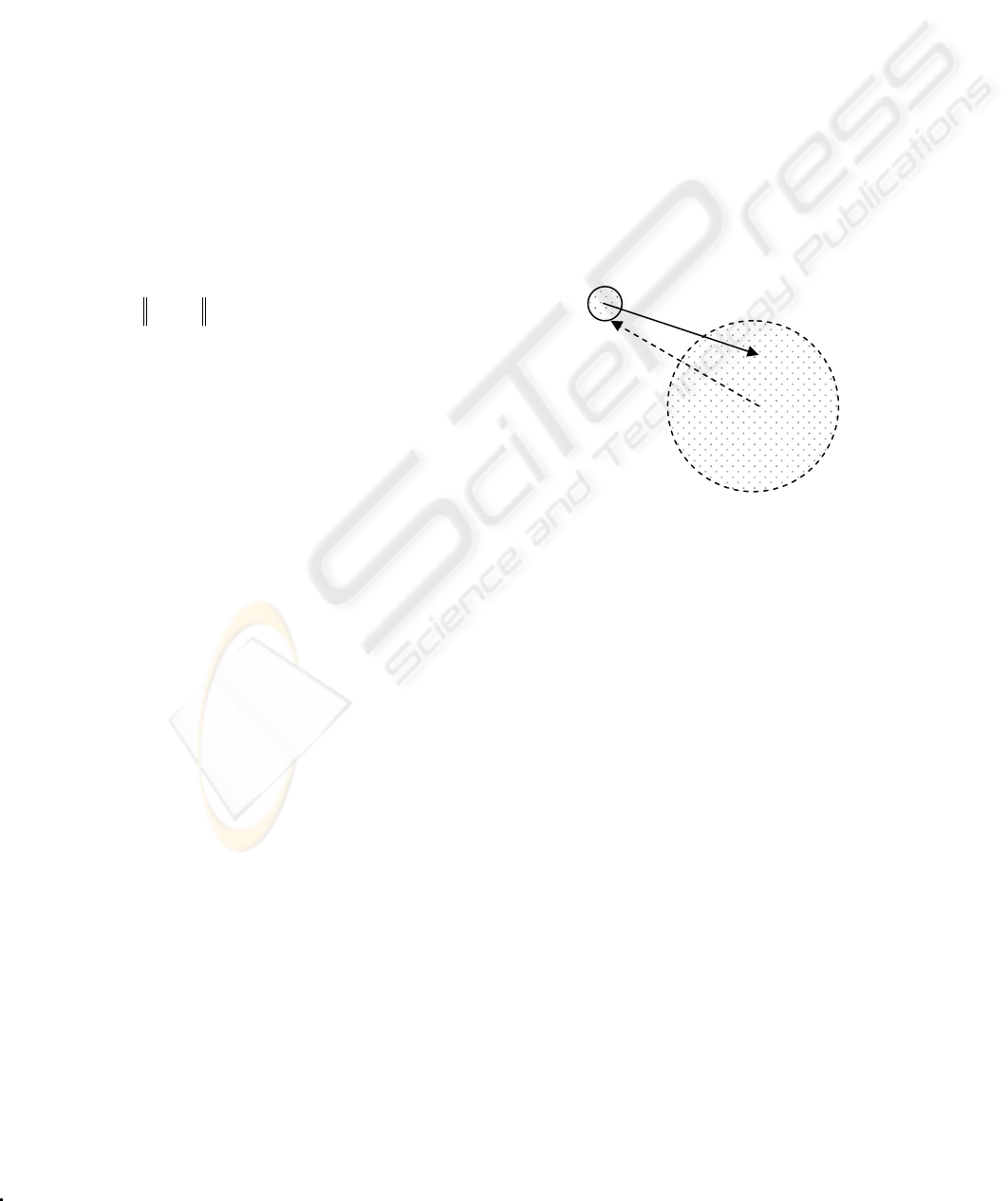
This can be demonstrated in Fig.2. If a point of set

has a larger divergence than the points of set

B as

illustrated in Fig.2, then, each point of its

neighbourhood in

A have similar divergence that are

more than divergences of the points of

B. Thus, the

control points will be selected from set

A rather than

set

B. It is clear that in this manner, the distribution

of the selected control points will not be uniform

over the original data point set. Therefore, it is

necessary to further require that each control point

should hold a large divergence with respect to all the

control points

BA∪ , so that the control points can

be distributed over the original data point set as

uniformly as possible. The divergence of each point

x is computed as follows,

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

−−=

⎟

⎠

⎞

⎜

⎝

⎛

−−=

∑

∈

))((2

))((1

iii

trdiv

xyxy

xxxx

, (7)

where,

S is the data point set while

S is the control

point set. The control point

x is selected using

(

)

divdiv 21maxarg

, where arg(·) extracts

the point

x which yields the maximum of

(

)

divdiv 21

Figure 2: The divergence of different point sets. The

points in A have a similar divergence that is larger than the

divergence of the points in B.

However, the implementation of Eq.(7) is time-

consuming. In practice, we prefer to use a standard

clustering algorithm (Duda et al. 2001) instead. For

clarity, some concepts need to be first defined as

follows.

z Centre of a partition

P is regarded as clustering

centre, which is defined as,

()()

)()()(

,,maxarg SPtr

∈∈

⎟

⎠

⎞

⎜

⎝

⎛

−−=

∑

∈

yxxxxxy

;

z Measure between two points,

(

)

Strd

jijiij

∈−−= xxxxxx ,,))(( ;

Based on the above definitions, our Partition

Algorithm can be stated as follows:

{Clustering}

{Initializing}: Input data point set S, centre

set

S and an initial partition SP

∪ ;

VISAPP 2006 - IMAGE UNDERSTANDING

176

{Merging, Splitting and Deleting}: These

standard clustering operations are carried out based

on the above definitions of the measure

d and the

selected centre

∈y ;

Iteration until there is no change in each

P ;

{Partitioning G}

Loop: from i=1 to r

Partition G in terms of

P ;

EndLoop;

The proposed partition algorithm is a divergence-

based iterative approach. The initial centre set

S is

usually the point set with the first r maximum

singular values of columns of G. The measure

between two points is indeed another representation

of the Euclidean distance. It can make the centers of

partitions as divergent as possible. But the clustering

algorithm is only an approximation of Eq.(7). Thus,

our partition algorithm can only approximate the

global optimal partition.

In short, the presented partition-based SVD

approach and partition algorithm constitute our

SVD-based approach for dataset simplification. It is

clear that data redundancy and computational

complexity of the large-sized range dataset can be

effectively amended in this SVD-based approach.

The highlight property of this approach is that the

control points are not fixed in advance. This means

that the basis functions can be modified adaptively

in terms of the change of range dataset. The

resulting solution of Eq.(2) would be a global least

square solution.

4 EXPERIMENTS AND

ANALYSIS

An intuitional way to evaluate the data point

simplification is to visualize the resulting implicit

surface. Our experiments of simplifying dataset are

first carried out on a range dataset of human faces

for a detailed analysis. The original range dataset

includes about 35,000 points, which is meshed and

illustrated in Fig.3a.

In the first experiment, we apply the pseudo-inverse

approach to this dataset. About 2,100 control points

are chosen uniformly over the whole dataset. The

resulting surface is shown in Fig.3b. Due to the

reduction of the control points, many details of the

face are lost. However, it can be noted that the

essential structures are preserved. Clearly, the

control points determine the essential structures of

the face in the resulting implicit surface. When the

control points are chosen uniformly over the whole

original dataset, the essential features can be

unbiasedly chosen as the control points. Indeed, the

influence of the non-control points in Eq.(5) is very

limited. We also show the resulting surface only

based on the control points in Fig.3c (i.e. non-

control points are not used). Obviously, the variance

between Fig.3b and Fig.3c is very small.

Furthermore, reducing the number of control points

to about 1,100, we fit the surface on the basis of a

selected control point set. The resulting surface is

shown in Fig.3d. It can be noted that there are no

distinct details lost in Fig.3d compared with Fig.3c.

This indicates that uniform sampling can preserve

the essential structures of the face. But it can also be

noted that distortions are also visible around the

nose in Fig.3d.

In the second experiment, we apply the SVD-based

approach to the same range dataset as in Fig.3a. In

this approach, the partition of G dominates the

quality of the resulting surface. Thus, the two

criteria of Eq.(7) become highlighted. In our

experiment, we first consider the first criterion of

Eq.(7), i.e.

⎟

⎠

⎞

⎜

⎝

⎛

−−=

∑

∈Sx

iii

trdiv ))((1 xxxx , as the

criterion of partition. Herein, the Partition Algorithm

described in section 3.2 is simply replaced by sorting

{

}

div1 . The control points are reduced to 30,000,

10,000 and 6,000 points respectively. The resulting

surfaces are shown in Fig.4. It can be noted that due

to the non-uniformity of the control points, many

structures are lost. Clearly, some regions contain few

or no control points (such as the nose area) while

others contain an excess of control points (such as

the cheek area). However, the essential facial

outlines are still retained. Moreover, when we

consider the two criteria of Eq.(7), i.e. use the

partition algorithm to obtain an appropriated

partition of G, it can be noted that some details of

the face can also be preserved even if the control

points are further reduced. The resulting surfaces

with the different numbers of control points are

shown in Fig.5.

Furthermore, comparing our SVD-Based Approach

with the uniformed down-sampling approach, we

can compare Fig.5c and Fig.5d with Fig.3c and

Fig.3d. This is because in Fig.3c and Fig.3d, we

uniformly down-sampled the control points over the

original range dataset, and the other non-control

points were discarded. In addition, the number of

control points in Fig.3c and Fig.3d are similar to the

number of control points in Fig.5c and Fig.5d

respectively. It can be noted that Fig.5c and Fig.5d

appear more distinct and preserve more details than

SIMPLIFIED REPRESENTATION OF LARGE RANGE DATASET

177

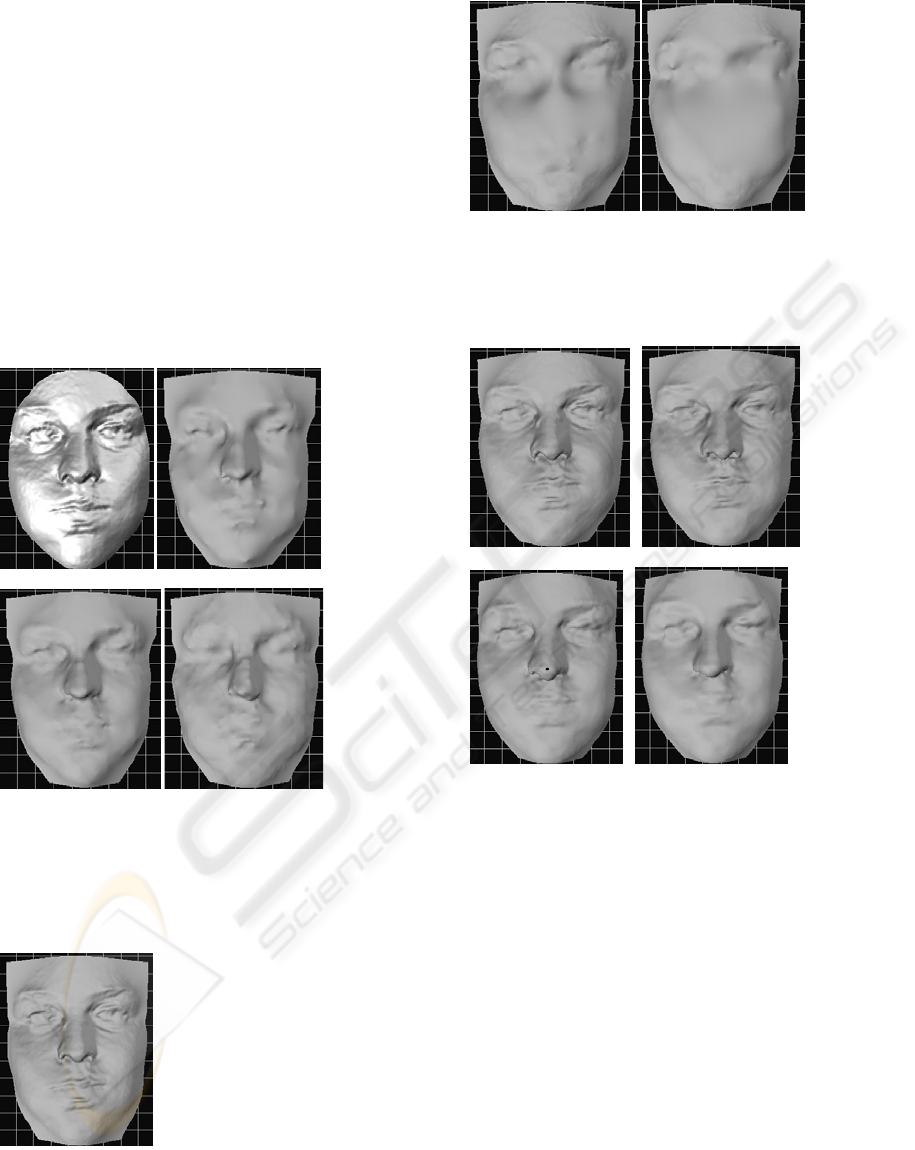
Fig.3c and Fig.3d, and there are comparatively less

distortions in Fig.5c and Fig.5d.

In order to further verify the efficiency of the SVD-

Based Approach, we subsequently apply the SVD-

Based Approach to 5 range datasets with different

facial expressions. The original numbers of data

points are in the range of 32,000-35,000, and are

reduced to 1,100 through our SVD-Based Approach.

For comparison, we also apply the uniform sampling

approach to these 5 range datasets, and their point

numbers are also reduced to about 1,100. All the

resulting surfaces are shown in Fig.6. It can be noted

that the resulting surfaces obtained by the SVD-

Based Approach preserve more details, and have

less distortions compared to the ones obtained by the

uniform sampling approach.

a. b.

c. d.

Figure 3: The resulting surfaces through the Pseudo-

Inverse Approach. a) original model, b) result using

pseudo-inverse approach, c) result using uniform sampling

approach, d) result using uniform down-sampling

approach, in which the number of points is reduced to

about 1,100.

a. 30,000 points

b. 10,000 points c. 6,000 points

Figure 4: The facial model is simplified by the SVD-based

approach with the first criterion of Eq.(7). Non-uniform

sampling leads to the quality of the resulting surfaces

decreasing quickly.

a. 10,000 points b. 6,000 points

c. 2,000 points d. 1,100 points

Figure 5: The facial model is simplified by the SVD-based

approach with the two criterion of Eq.(7). Considering the

uniform sampling preserves many details effectively.

5 CONCLUSIONS

In this paper, we presented two approaches of

computational simplification for medium- or large-

sized range dataset, one is the Pseudo-Inverse

Approach, and the other is the SVD-Based

Approach. The novelty in this paper is that we

devised a novel partition-based SVD algorithm,

which can effectively reduce the dimension of a

symmetric square matrix in a given partition case.

We combined the partition-based SVD algorithm

with a standard clustering algorithm to form our

SVD-Based Approach. Experimental results indicate

that in a given control point set case, the Pseudo-

Inverse Approach can give an optimal solution in a

least square sense. While in the case of an unknown

VISAPP 2006 - IMAGE UNDERSTANDING

178

control point, the SVD-Based Approach can seek an

appropriate control point set automatically, and the

resulting surface can preserve more details and

generate less distortions.

REFERENCES

Carr, J.C. and Beatson, R.K. et al., 2003. Smooth surface

reconstruction from noisy range data, ACM

GRAPHITE 2003, Melbourne, Australia, pp.119-126.

Carr, J.C. and Beatson, R.K. et al., 2001. Reconstruction

and Representation of 3D Objects with Radial Basis

Functions, ACM SIGGRAPH 2001, Los Angeles, CA,

pp.67-76.

Carr, J.C., Fright, W.R. and Beatson, R.K., 1997. Surface

Interpolation with Radial Basis Functions for Medical

Imaging, IEEE Transactions on Medical Imaging, Vol.

16, No. 1, pp.96-107.

Morse, B.S. and Yoo, T.S. et al., 2001. Interpolating

Implicit Surfaces from Scattered Surface Data Using

Compactly Supported Radial Basis Functions, in Proc.

of the Intel Conf on Shape Modeling & Applications,

pp.89-98.

Fleishman, S., Cohen-Or, D. and Silva, C.T., 2005. Robust

moving least-squares fitting with sharp features, ACM

Transactions on Graphics, Vol.24, Issue 3.

Beatson, R.K., Cherrie, J.B. and Mouat, C.T., 1999. Fast

fitting of radial basis functions: Methods based on

preconditioned GMRES iteration, Advances in

Computational Mathematics, Vol.11, pp.253–270.

Beatson, R.K., Cherrie, J.B. and Ragozin, D.L., 2001. Fast

evaluation of radial basis functions: Methods for four-

dimensional polyharmonic splines, SIAM J. Math.

Anal., Vol.32, No.6, pp.1272–1310.

Beatson, R.K., Light, W.A. and Billings, S., 2000. Fast

solution of the radial basis function interpolation

equations: Domain decomposition methods, SIAM J.

Sci. Comput., Vol.22, No.5, pp.1717–1740.

Suter, D., 1994. Fast evaluation of splines using poisson

formula. Intl. J. of Scientific Computing and

Modeling, Vol.1, No.1, pp.70–87.

Yu, H.C. and Bennamoun, M., 2005. Simplified

Representation of Large Range Dataset, Technical

Report, School of CSSE, Univ. of Western Australia.

Duda, R.O., Hart, P.E. and Stork, D.G., 2001. Pattern

Classification (2nd ed.), Wiley Interscience

SIMPLIFIED REPRESENTATION OF LARGE RANGE DATASET

179