SURFACE REGISTRATION USING LOCAL SURFACE EXTENDED

POLAR MAP

Elsayed E. Hemayed

Cairo University

Computer Engineering Department, Faculty of Engineering, Giza, Egypt

Keywords:

Surface Registration, Surface Signature, Surface Matching, 3D Object Representation.

Abstract:

In this paper, we are presenting a new surface signature-based representation that is orientation-independent

and can be used to match and align surfaces under rigid transformation. The proposed scheme represents

the surface patches in terms of their signatures. The surface signatures are formed as extended polar maps

using the neighbours of each surface patch. Correlation of the maps is used to establish point correspondences

between two views; from these correspondences a rigid transformation that aligns the views is calculated. The

effectiveness of the proposed scheme is demonstrated through several registration experiments.

1 INTRODUCTION

Many applications require the construction of precise

3D object models of physical objects, preserving as

much information as possible (Bernardini et al., 2002;

Ikeuchi and Sato, 2001). It is usually necessary to

scan the scene from different viewpoints in order to

build a complete 3-D model of a complex scene. The

registration of the acquired data sets into a common

coordinate system has been a subject of much re-

search during the last 15 years.

Several of the proposed methods (Rusinliewicz and

Levoy, 2001; Zhang et al., 2004; Blais and Levine,

1995; Zhang, 1994; Eggert et al., 1997; Okatani and

Sugimoto, 2004; Sharp et al., 2002) can be seen as

extensions or improvements of the Iterative Closest

Point (ICP) algorithm (Besl and McKay, 1992). ICP

is an iterative procedure minimizing the mean squared

error (or the sum of the squared distances) between

points in one view and the respective closest points in

the other view. At each ICP iteration, the geometric

transformation that best aligns the two images with

respect to this criterion is calculated.

Another approach (Fan et al., 2002; Robertson and

Fisher, 2002; Silva et al., 2005) to registering two im-

ages is to ﬁnd the geometric transformation through

a pose-space search, rather than the correspondence-

based search of ICP. The search space of geometric

transformations contains solutions that can be used to

align two views. In this case, the objective is to ﬁnd,

in a huge search space, a solution acceptably close to

the global optimum, in a reasonable time.

Recently, researchers have developed and dis-

cussed different surface representations that are ef-

fective in ﬁnding point corresponding between the

two sets to be registered. In this case, the reg-

istration problem is addressed in two steps, where

the ﬁrst step is to establish the point correspond-

ing between the surface sets then to use these points

to compute the transformation that aligns the two

surfaces. These surface representations are known

as surface signature-based representation. They in-

clude the splash representation (Stein and Medioni,

1992), the point signatures (Chua and Jarvis, 1997),

the spin image representation (Johnson and Hebert,

1999), the spherical spin image representation (Cor-

rea and Shapiro, 2001), the surface point signatures

(Yamany and Farag, 2002), the harmonic shape im-

ages (Zhang and Herbert, 1999), the local surface de-

scriptors (Chen and Bhanu, 2004) and the point ﬁn-

gerprints (Sun et al., 2003). In this paper, we are

proposing an extension for these representations to

solve the registration problem.

The proposed representation technique, Local Sur-

face Extended Polar Map (L-SEPMap), transforms

the surface from the Cartesian coordinate system

where surface descriptions vary with transformation

to an extended polar coordinate system where sur-

face descriptions are invariant to rigid transformation.

In this artiﬁcial domain, every surface patch, its cen-

143

E. Hemayed E. (2006).

SURFACE REGISTRATION USING LOCAL SURFACE EXTENDED POLAR MAP.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 143-148

DOI: 10.5220/0001375601430148

 SciTePress

ter of gravity, is represented by one L-SEPMap. As

a surface signature-based representation, L-SEPMap

places few restrictions on object shape and topology

and can be used to match surfaces in the presence of

clutter and occlusion.

Our approach to solve the surface registration prob-

lem is based on establishing point correspondences

using the L-SEPMap scheme. Next, sets of geo-

metrically consistent point correspondences are used

to compute the transformation that aligns the views

(Williams and Bennamoun, 2001).

This paper is organized as follows: The L-SEPMap

scheme is described in Section 2. The alignment pro-

cess using L-SEPMap scheme is described in Section

3. Experimental results are presented and discussed

in Section 4. Finally, conclusion and future work are

presented in Section 5.

2 L-SEPMap SCHEME

In this paper, surfaces are deﬁned by a dense col-

lection of 3D points and surface normals (Hemayed,

2003). In L-SEPMap, we are extending the surface

signature representation to calculate the signature of

neighbor points only. Our approach is to use three

parameters (θ, φ, r) to represent the positions and the

curvature of each point with respect to the basis of

other neighbor points on the surface. In this represen-

tation, (θ, φ) capture the relative curvature while ’r’

captures the relative displacement between the sur-

face points. The three parameters are transformation

(rotation and translation) invariant.

L-SEPMaps generated for two corresponding

points on different surfaces would be similar, so ori-

ented points can be matched based on a compari-

son of their L-SEPMaps. L-SEPMaps are descrip-

tive enough that correspondences between points can

be established based on a comparison of L-SEPMaps

alone. Since L-SEPMaps is based on the neighbor

locality of the surface’s points of an object, the pro-

posed algorithm will generate a representation that is

robust to clutter and occlusion, so segmentation of

scene data is not necessary for surface matching in

cluttered scenes. In addition, the locality nature of

the L-SEPMap representation speeds up the process

and save the system memory. The process of generat-

ing the L-SEPMaps are presented in this section along

with the object model representation.

2.1 Object Model Representation

The object model is deﬁned by a set of triangles. Each

triangle composed of three-vertices deﬁned by their

Cartesian coordinates in the object coordinate sys-

tems. In order to simplify the L-SEPMap generation

process, the triangle’s center-of-gravity and its normal

are used instead of the actual triangle. So the object

model can be seen as a set of oriented points (repre-

sent the triangle’s center-of-gravity) and the surface

normal at these points. Mathematically, the object

model is deﬁned by Eq. 1.

G = {g

= (p, n

)

, i = 1..N } (1)

Where p = (x, y, z) is the Cartesian coordinate of the

triangle’s center of gravity and n

= (n

, n

) is

the triangle’s surface normal. g is known as an ori-

ented point.

2.2 L-SEPMap Generation

In the L-SEPMap generation process, each surface

patch (triangle) in the model is represented by a map

that is independent of the object coordinate system.

The map is generated at each surface patch by record-

ing the relative curvature and displacement of that sur-

face patch and its neighbors surface patches in the

model. The following terms are helpful in explaining

the generation process.

Neighbor Degree: This term is used to indicate

how two oriented points are close to each other. For

example, if an oriented point p is adjacent to another

oriented point q, i.e., their triangle patches share one

side, then we say that p is a neighbor to q with degree

1. And if w is not adjacent to p but it is adjacent to

q, then w is a neighbor to p with degree 2 and so on.

Fig. 1(a-c) shows the neighbors of a triangle patch for

1-, 2-, and 3-degree.

L-Degree Neighbors P

(g): This is the set of

all points that are neighbors to point g with degree

1, 2, ..L. If a point has an L-degree neighbors then

it may have an L+1 degree neighbors. However, if a

point does not have L-degree neighbors then it will

not have neighbors of any degree higher than L. We’ll

say that a point does not have an L-degree neighbors

if any of its L-1 degree neighbors has any of its side at

the edge of the model and as such it is not shared with

any other patch in the model. Fig. 1(d) illustrates that

triangle patch 1 and 2 lie on the edge and as such the

shaded triangle patch does not have a 4-degree neigh-

bors.

Inner Points of L-Degree: This is the set of all

oriented points that have at least L-degree neighbors.

In the other side, those points who do not have an L-

degree neighbors, they will be known as outer points

of L-degree. Fig. 1(d) shows that the shaded trian-

gle patch (oriented point) can be considered an inner

patch (oriented point) of 3-degree but an outer point

in case of 4 or higher neighbor degree.

For an object model G deﬁned by Eq. 1, the L-

SEPMap M of an oriented point g ∈ G, g = (p, n

)

is deﬁned by Eq. 2 (where N

is the number of L-

VISAPP 2006 - IMAGE UNDERSTANDING

144

(a) (b)

Figure 1: The neighbors of the shaded triangle patch of (a-

c) 1-, 2-, and 3-degree, respectively. (d) Patches 1 and 2 are

edge patches.

Degree neighbors P

(g)), and is generated as fol-

lows:

= {m

= (θ, φ, r)

, j = 1..N

} (2)

For each oriented point g

∈ P

(g), g

= (q, n

)

1. Deﬁne v = the vector

−→

pq,

2. Calculate (θ, φ, r) as follows, see Fig. 2.

(a) θ = the angle between n

and v

(b) φ = the angle between n

and v

3. Record m

= (θ, φ, r) in M

The L-SEPMap generation process is repeated for

all inner points of L-degree g

∈ G, each will pro-

duce an L-SEPMap, M

, i = 1..N . The set of L-

SEPMaps are used to represent the object model G.

So the model L-SEPMap representation G

is deﬁned

= {M

, i = 1..N },

= {m

= (θ, φ, r)

, j = 1..N

}

(3)

where N is the number of inner points of L-degree

in the model G and N

is the number of L-Degree

neighbors of the point g

3 REGISTRATION PROCESS

USING L-SEPMaps

The problem of registering two different surfaces de-

ﬁned by their L-SEPMaps is solved in a two-step

Figure 2: The calculation of an L-SEPMap tuple

m = (θ, φ, r) of two oriented points (p, n

) and (q, n

process, L-SEPMap matching and the transformation

matrix estimation. In the ﬁrst step, the L-SEPMaps

of the two surfaces’s points are matched establish-

ing points corresponding between the two surfaces.

The matched points are then fed into the second step

where a modiﬁed ICP algorithm is used to estimate

the rotation and translation matrices to align the two

surfaces. The L-SEPMap matching and the transfor-

mation estimation are presented in this section.

3.1 L-SEPMap Matching

The idea of the L-SEPMap matching is to establish

point corresponding between the two surfaces that

maximize the similarity between them. In our case,

the two objects are represented by their L-SEPMaps.

Mathematically, the L-SEPMap matching problem is

deﬁned as follows:

Given the L-SEPMap representation of two objects

G = {M

, i = 1...N

H = {M

, i = 1...N

}

(4)

where N

and N

are the number of oriented points in

G and H, respectively. Find the point correspondence

between the two objects that maximizes the similarity

between them.

Let’s deﬁne the term Candidate Match Pair. This

term is used to indicate that two map points m

(θ, φ, r)

and m

= (θ, φ, r)

form a possible match

pair. m

and m

are possible match pair if they have

similar relative curvature and displacement, that is

≈ θ

, φ

≈ φ

and r

≈ r

In order to measure the similarity between two ob-

jects G and H, we ﬁrst measure the similarity, P , be-

tween their pair-wise L-SEPMaps deﬁned in Eq. 4.

The similarity, P , between two L-SEPMaps, M

and

, deﬁned in Eq. 5, is measured by the percentage

of matching records between the two L-SEPMaps.

Given two L-SEPMaps

= {m

= (θ, φ, r)

, i = 1..N

= {m

= (θ, φ, r)

, j = 1..N

}

(5)

SURFACE REGISTRATION USING LOCAL SURFACE EXTENDED POLAR MAP

145

The matching process can be summarized in the

following steps:

1. ∀M

∈ G and M

∈ H, calculate the similarity

measure, P

as follows:

(a) Count the number of candidate match pair be-

tween all m

∈ M

and m

∈ M

(b) The similarity measure between M

and M

, is the maximum count recorded in the pre-

vious step.

> ∆ then M

and M

are said to be a

matched pair. ∆ is used to account for sampling

noise.

2. The overall similarity measure, P , between G and

H, is determined by a simple counting approach.

First, we form matching pairs between each M

∈

G and M

∈ H such that each will appear only

once in all the matching pairs. Since M

can have

several match with M

, we keep only the match

that have higher similarity measure P

. The num-

ber of matching pairs formed is considered to be

the overall similarity measure P .

The matching pairs formed during the matching

process is the corresponding list that is fed into the

second step where a modiﬁed ICP algorithm is used to

estimate the rotation and translation matrices to align

the two surfaces.

3.2 Transformation Matrix

Estimation

The aim of the registration process is to compute the

transformations, which, when applied to the points

in that view, it brings the two surfaces into align-

ment. The desired transformations are expressed by

the 3x3 rotation matrix R and 3x1 translation vectors

t. The registration procedure can be posed as the min-

imization of a cost function which measures the sum

of squared distances between the transformed corre-

sponding points.

E =

i=1

j=1

− (Rp

+ t)

, (6)

1 if (p

, p

) forms pairwise correspondence

0 otherwise

where N

and N

are the numbers of points in the

two surfaces. The Iterative Closest Point (ICP) algo-

rithm proposed by Besl and McKay (Besl and McKay,

1992) is a commonly used framework for solving this

surface registration problem. In our work, we used

an enhanced ICP algorithm, developed by Williams

and Bennamoun (Williams and Bennamoun, 2001) to

solve the registration problem.

4 EXPERIMENTAL RESULTS

The registration process using SEPMap scheme has

been applied to several object models. In this paper,

we present the results of experimenting with four ob-

ject models (from 3D CAFE website); a chess king,

rook, queen, and bishop as shown in Fig. 3.

In the ﬁrst experiment, we applied rigid transfor-

mation (rotation, translation) to the four whole-sized

models to form our full-size object set. Fig. 4 shows

the model and the transformed object. Table 1 shows

the transformation parameters of the experimental ob-

jects. The transformation parameters shown are the

rotation axis, rotation angle and the translation vec-

tor.

In the second experiment, we simulate a form of

occlusion where the object does not have a complete

3D-model. In this experiment, we cut a piece of the

models and applied to it rigid transformation to form

our partial-size object set. Fig. 5 shows the model and

the transformed partial-sized object. The transforma-

tion paramters are shown in Table 2.

the registration process using L-SEPMap scheme

has been applied to the full-size object sets and their

corresponding model. Fig. 6 shows the object and

the model after registration. Models are shown in

light grey-level (gold color) while objects are shown

in dark grey-level (purple color).

Similarly, the registration process using L-SEPMap

scheme has been applied to the partial-size object sets

and their corresponding model. Fig. 7 shows the ob-

ject and the model after registration.

To verify the accuracy of the registration process,

we calculate the sum of the squared distance error, de-

ﬁned in Eq. 6. Table 3 shows the registration errors of

the registration experiments. The results demonstrate

the effectiveness of the proposed technique visually

and analytically. and the ability of the technique in

handling the general registration problem of full and

partial objects.

All experiments were conducted in a laptop com-

puter with Pentium-M processor 1.8 GHz and 512

MB RAM and assuming 5-degree of neighbors. The

average L-SEPMap generation total time (user + I/O +

CPU) is less than 2 seconds in a model of 1000 orig-

inal triangles. The matching total time (registration

time is negligible) between a model and object with

1000 triangle patches is less than 10 seconds. The

computational and memory requirements are propor-

tional to the number of original triangle patches and

the neighbors degree selected in the generation pro-

cess and can be reduced by applying the L-SEPMap

scheme to selected surface patches instead of the com-

prehensive search applied in this paper.

VISAPP 2006 - IMAGE UNDERSTANDING

146

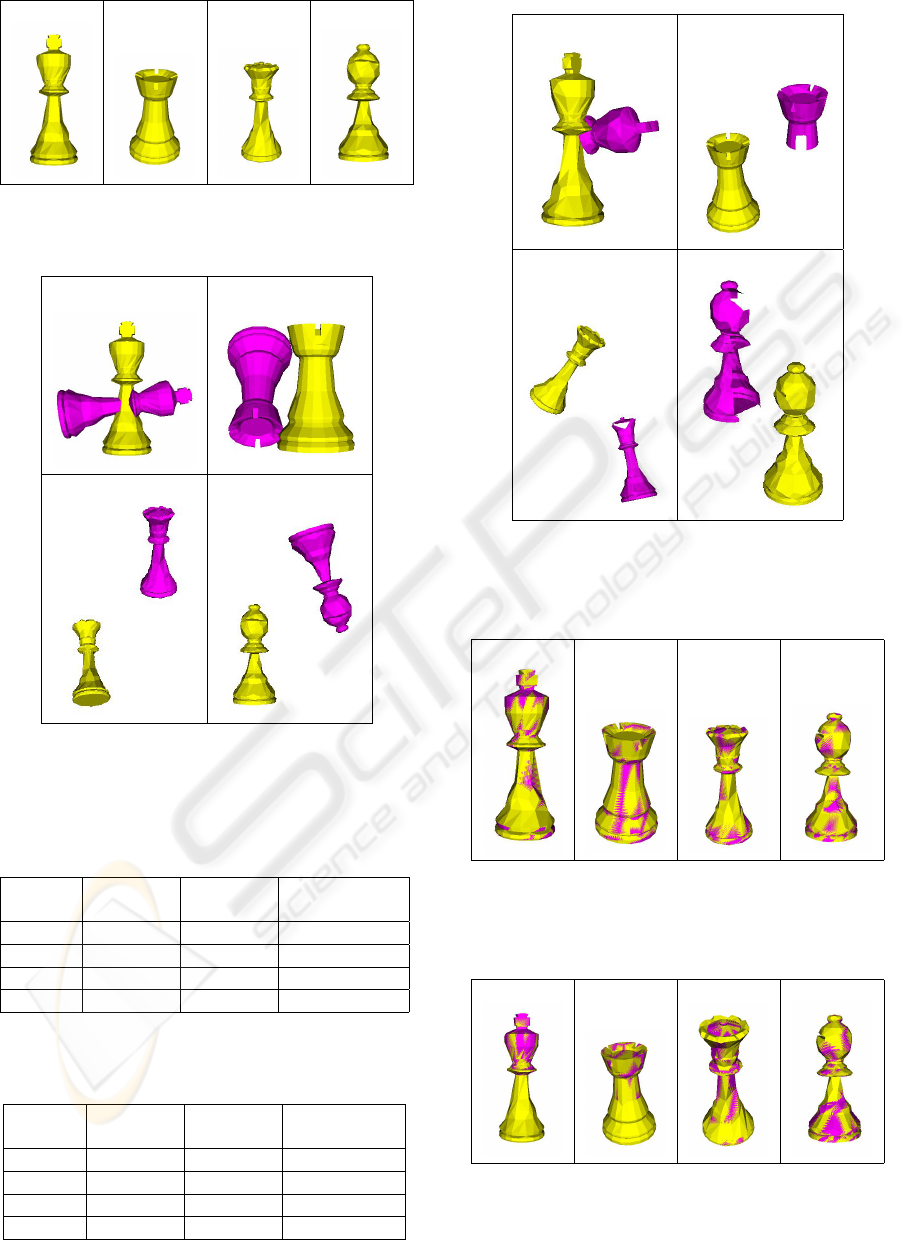
Figure 3: The models library, four chess pieces models,

from left to right, king, rook, queen, and bishop.

Figure 4: The models (yellow or light) and their trans-

formed objects (pink or dark).

Table 1: Transformation parameters for the full-size ob-

jects.

Rotation Rotation Translation

Axis Angle Vector

King z-axis 30 [00, -05, 00]

Rook y-axis 15 [-20, 00, -20]

Queen x-axis 45 [30, 30, 33]

Bishop z-axis 60 [30, 30, 20]

Table 2: Transformation parameters for the partial-size ob-

jects.

Rotation Rotation Translation

Axis Angle Vector

King x-axis -30 [04, 00, 00]

Rook y-axis -45 [30, 30, 20]

Queen x-axis -45 [30, -20, 30]

Bishop y-axis 60 [-15, 20, 20]

Figure 5: The models (yellow or light) and the transformed

partial objects (pink or dark).

Figure 6: The models (yellow or light) and the transformed

objects (pink or dark) after registration.

Figure 7: The models (yellow or light) and the transformed

partial objects (pink or dark) after registration.

SURFACE REGISTRATION USING LOCAL SURFACE EXTENDED POLAR MAP

147

Table 3: The registration errors.

Object Full Object Partial Object

King 0.2174 0.0001

Rook 0.0001 0.0844

Queen 0.0001 0.0001

Bishop 0.1011 0.0460

5 CONCLUSION AND FUTURE

WORK

L-SEPMap is a surface signature-based representa-

tion scheme that is orientation-independent and can

be used to align surfaces under rigid transformation.

The experimental results demonstrate the effective-

ness of the proposed technique and the ability to han-

dle general registration problem of full and partial ob-

jects. Several items will be considered in future work.

Among those items are , studying the impact of noise

on the discrimination effectiveness of the L-SEPMap,

experimenting with clutter scenes and different trian-

gulation sampling, applying the L-SEPMap scheme

to the 3D segmentation problem, and extending the

matching algorithm to handle uniform scaling.

REFERENCES

Bernardini, F., Martin, I., Mittleman, J., Rushmeier, H.,

and Taubin, G. (2002). Building a digital model

of michelangelo’s ﬂorentine pieta. IEEE Computer

Graphics & Applications, 22(1):59–67.

Besl, P. and McKay, N. (1992). A method for registration

of 3-d shapes. IEEE Trans. on PAMI, 14(2):239–256.

Blais, G. and Levine, M. D. (1995). Registering multiview

range data to create 3d computer objects. IEEE Trans.

on PAMI, 17(8):820–824.

Chen, H. and Bhanu, B. (August 2004). 3d free-form ob-

ject recognition in range images using local surface

patches. In Proc. of the 17th Int. Conf. on Pattern

Recognition, pages 524–530, Cambridge, UK.

Chua, C. S. and Jarvis, R. (1997). Point signatures: A

new representation for 3-d object recognition. Inter-

national Journal of Computer Vision, 25(1):63–85.

Correa, S. and Shapiro, L. (2001). A new signature-based

method for efﬁcient 3-d object recognition. In Proc.

IEEE CVPR, volume 1, pages 769–776.

Eggert, D. W., Lorusso, A., and Fisher, R. B. (1997). Es-

timating 3d rigid body transformations: a comparison

of four major algorithms. Machine Vision and Appli-

cations, 9:272–290.

Fan, Y., Jiang, T., and Evans, D. (2002). Medical image

registration using parallel genetic algorithms. LNCS

(Applications of Evolutionary Computing), 2279:304–

314.

Hemayed, E. (July 2003). A scalable approach for 3d

mesh generation. In Proc. of the 7th World Multi-

Conference on Systemics, Cybernetics and Informat-

ics, Oralndo, FL.

Ikeuchi, K. and Sato, Y., editors (2001). Modeling From

Reality. Kluwer Academic Publishers.

Johnson, J. and Hebert, M. (1999). Using spin images

for efﬁcient object recognition in cluttered 3d scenes.

IEEE Trans. on PAMI, 21(5):433–449.

Okatani, I. and Sugimoto, A. (2004). Registration of

range images that preserves local surface structures

and color. In Proc. of the 2nd International Sym-

posium on 3D Data Processing, Visualization, and

Transmission (3DPVT’04), pages 789–796.

Robertson, C. and Fisher, R. (2002). Parallel evolutionary

registration of range data. Computer Vision and Image

Understanding, 87(1):39–50.

Rusinliewicz, S. and Levoy, M. (2001). Efﬁcient variants

of the icp algorithm. In Proc. of the 3th Int. Conf. on

3-D Digital Imaging and Modeling, volume 1, pages

145–152.

Sharp, G. C., Lee, S. W., and Wehe, D. K. (2002). ICP

registration using invariant features. IEEE Trans. on

PAMI, 24(1):90–102.

Silva, L., Bellon, O. R. P., and Boyer, K. L. (2005). Pre-

cision range image registration using a robust surface

interpenetration measure and enhanced genetic algo-

rithms. IEEE Trans. on PAMI, 27(5):762–776.

Stein, F. and Medioni, G. (1992). Structural indexing: ef-

ﬁcient 3-d object recognition. IEEE Trans. on PAMI,

14(2):125–145.

Sun, Y., Paik, J., Koschan, A., Page, D. L., and Abidi, M. A.

(2003). Point ﬁngerprint: A new 3-d object represen-

tation scheme. IEEE Trans. On Systems, Man and Cy-

bernetics - Part B: Cybernetics, 33(4):712–717.

Williams, J. and Bennamoun, M. (2001). Simultaneous reg-

istration of multiple corresponding point sets. Com-

puter Vision and Image Understanding, 81(1):117–

142.

Yamany, S. M. and Farag, A. A. (2002). Surface sig-

natures: An orientation independent free-form sur-

face representation scheme for the purpose of objects

registration and matching. IEEE Trans. on PAMI,

24(8):1105–1120.

Zhang, D. and Herbert, M. (1999). Harmonic maps and

their applications in surface matching. In Proc. IEEE

Conf. CVPR, volume 2, pages 524–530.

Zhang, H., Hall-Holt, O., and Kaufman, A. (June 2004).

Range image registration via probability ﬁeld. In

Proc. of the Computer Graphics International, pages

546–552, Crete, Greece.

Zhang, Z. (1994). Iterative point matching for registra-

tion of freeform curves and surfaces. IEEE Trans. on

PAMI, 13(2):119–152.

VISAPP 2006 - IMAGE UNDERSTANDING

148