A NEW APPROACH FOR THE TRUST CALCULATION IN
SOCIAL NETWORKS
Mehrdad Nojoumian, Timothy C. Lethbridge
School of Information Technology and Engineering, University of Ottawa, Ottawa, ON, K1N 6N5
Keywords: Trust, Reputation, Social Networks.
Abstract: This paper aims at the trust calculation in social networks by addressing some major issues: Firstly, the
paper evaluates a specific trust function and its behaviors, and then it focuses on the modification of that
trust function by considering diverse scenarios. After that, the paper proposes a new approach with a
specific functionality. The main goals are to support good agents strongly, block bad ones and create
opportunities for newcomers or agents who want to show their merit in our society although we can not
judge them. Finally, a mathematical discussion by a new trust function is provided with ultimate results.
1 INTRODUCTION
One of the major challenges for electronic
commerce is how to establish a relationship of trust
between different parties and how to form a
reputation scheme as a global vision. In many cases,
the parties involved may not ever have interacted
before. It is important for participants such as
buyers, sellers and partners to estimate each other’s
trustworthiness before initiating any commercial
transactions.
According to (
Mui, 2002), “Trust” is a personal
expectation an agent has about another’s future
behavior, it is an individual quantity calculated
based on the two agents concerned in a present or
future dyadic encounter while “Reputation” is
perception that an agent has of another’s intentions,
it is a social quantity calculated based on actions by
a given agent and observations made by others in a
social network. From the cognitive point of view
(
Castelfranchi and Falcone, 1998), trust is made up of
underlying beliefs and it is a function of the value of
these beliefs. Therefore, reputation is more a social
notion of trust. In our lives, we each maintain a set
of reputations for people we know. When we have
to work with a new person, we can ask people with
whom we already have relationships for information
about that person. Based on the information we
gather, we form an opinion about the reputation of
the new person.
To form a pattern for agents, we should consider
a “social network” which is a social structure made
of nodes and ties. Nodes are individual actors within
the networks, and ties are relationships between the
actors. In E-commerce, social network refers to an
electronic community which consists of interacting
parties such as people or businesses.
Another concept is “reputation systems” which
collect, distribute and aggregate feedback about
participants’ past behavior. They seek to address the
development of trust by recording the reputations of
different parties. The model of reputation will be
constructed from a buying agent’s positive and
negative past experiences with the aim of predicting
how satisfied the buying agent will be with the
results of future interactions with a selling agent.
OnSale exchange and eBay are practical examples
of reputation management. OnSale allows users to
rate and submit textual comments about sellers. The
overall reputation of a seller is the average of the
ratings obtained from his customers. In eBay, sellers
receive feedback (-1, 0, +1) for their reliability in
each auction and their reputation calculated as the
sum of those ratings over the last six months. The
major goal of reputation systems is to help people
decide whom to trust and deter the contribution of
dishonest parties. Most existing online reputation
systems are centralized and have been designed to
foster trust among strangers in e-commerce (
Resnick
et al,
2000).
257
Nojoumian M. and C. Lethbridge T. (2006).
A NEW APPROACH FOR THE TRUST CALCULATION IN SOCIAL NETWORKS.
In Proceedings of the International Conference on e-Business, pages 257-264
DOI: 10.5220/0001429202570264
Copyright
c
 SciTePress

To extend reputation systems, a “social
reputation system” can be applied in which a buying
agent can choose to query other buying agents for
information about sellers for which the original
buying agent has no information. This system allows
for a decentralized approach whose strengths and
weaknesses lie between the personal and public
reputation system.
For creating a “reputation model”, researchers
apply various approaches. For example in (
Yu and
Singh, 2002), an agent maintains a model of each
acquaintance. This model includes the agent’s
abilities to act in a trustworthy manner and to refer
to other trustworthy agents. The first ability is
“expertise: ability to produce correct answers” and
the second one is “sociability: ability to produce
accurate referrals”. The quality of the network is
maximized when both abilities are considered.
The other essential factor is “social behavior”.
This refers to the way that agents communicate and
cooperate with each others. Usually, in reputation
systems good players are rewarded whereas bad
players are penalized by the society. For instance, if
A
1
encounters a bad partner (A
2
) during some
exchange, A
1
will penalize A
2
by decreasing its
rating and informing its neighbors. In a sample
proposed approach (
Yu and Singh, 2000), A
1
assigns a
rating to A
2
based on:
1. Its direct observations of A
2
2. The rating of A
2
as given by his neighbors
3. A
1
’s rating of those neighbors (witnesses)
Figure 1: A sample rating assignment.
As you can see, this approach seeks to create trust
based on local or social evidence; “local trust” is
built through direct observations while “social
trust” is built through information from others.
The purpose of this paper and our major
motivations are to evaluate the behavior of a specific
trust function and propose a new approach for the
modification of the trust calculation. The rest of this
paper is organized as follows. Section 2 reviews the
existing literature on the trust and reputation
systems. Section 3, illustrates the behavior of a
specific trust function and its modification by
proposing a new approach. Section 4, presents a
new trust function and shows the final results.
Finally in section 5, some concluding remarks are
provided.
2 LITERATURE REVIEW
In this section, we review many interesting
approaches in various research projects in order to
form a clear vision of trust and reputation systems.
Trust is one of the most important parameters in
electronic commerce technology. According to
(
Brainov and Sandholm, 1999), if you want to
maximize the amount of trade and of agents’ utility
functions, the seller’s trust should be equal to the
buyer’s trustworthiness; this shows the impact of
trust in E-commerce. Mui et al. (2002) summarize
existing works on rating and reputation across
diverse disciplines, i.e., distributed artificial
intelligence, economics, and evolutionary biology.
They discuss the relative strength of the different
notions of reputation using a simple simulation
based on “Evolutionary Game Theory”. They focus
on the strategies of each agent and do not consider
gathering reputation information from other parties.
A “Social Mechanism” of reputation
management was implemented in Kasbah (
Chavez
and Maes, 1996). This mechanism requires that users
give a rating for themselves and either have a central
agency (direct ratings) or other trusted users
(collaborative ratings).Yu and Singh (2003) present
an approach which understands referrals as arising
in and influencing “Dynamic Social Networks”
where the agents act autonomously based on local
knowledge. They model both expertise and
sociability in their system and consider a weighted
referral graph. Sabater and Sierra (2002) show how
social network analysis can be used as part of the
“Regret Reputation System” which considers the
social dimension of reputation. Pujol et al. (2002)
propose an approach to establish reputation based on
the position of each member within the
corresponding social networks. They seek to
reconstruct the social networks using available
information in the community.
Yolum and Singh (2004) develop a “Graph
Based Representation” which takes a strong stance
for both local and social aspects. In their approach,
the agents track each other's trustworthiness locally
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
258

and can give and receive referrals to others. This
approach naturally accommodates the above
conceptualizations of trust: social because the agents
give and receive referrals to other agents, and local
because the agents maintain rich representations of
each other and can reason about them to determine
their trustworthiness. Further, the agents evaluate
each other's ability to give referrals. Lastly, although
this approach does not require centralized
authorities, it can help agents evaluate the
trustworthiness of such authorities too.
To facilitate trust in commercial transactions
“Trusted Third Parties” (
Rea and Skevington, 1998)
are often employed. Typical TTP services for
electronic commerce include certification, time
stamping, and notarization. TTPs act as a bridge
between buyers and sellers in electronic
marketplaces. However, they are most appropriate
for closed marketplaces. Another method is from
“Social Interaction Framework (SIF)” (
Schillo et al.,
2000
). In SIF, an agent evaluates the reputation of
another agent based on direct observations as well
through other witnesses.
Breban and Vassileva (2001) present a
“Coalition Formation Mechanism” based on trust
relationships. Their approach extends existing
transaction-oriented coalitions, and might be an
interesting direction for distributed reputation
management for electronic commerce. Tan and
Thoen (2000) discuss the trust that is needed to
engage in a transaction. In their model, a party
engages in a transaction only if its level of trust
exceeds its personal threshold. The threshold
depends on the type of the transaction and the other
parties involved in the transaction.
In (
Yu et al., 2004) an agent maintains a model of
each acquaintance. This model includes the
acquaintance’s reliability to provide high-quality
services and credibility to provide trustworthy
ratings to other agents. Marti and Garcia-Molina
(2004) discuss the effect of reputation information
sharing on the efficiency and load distribution of a
P2P system, in which peers only have limited or no
information sharing. In their approach, each node
records ratings of any other nodes in a reputation
vector. Their approach does not distinguish the
ratings for service (reliability) and ratings for voting
(credibility) and does not consider how to adjust the
weight for voting.
Aberer and Despotovic (2001) use a model to
manage trust in a P2P network where no central
database is available. Their model is based on
“Binary Trust”. For instance, an agent is either
trustworthy or not. In case a dishonest transaction is
detected, the agents can forward their complaints to
other agents. Recently, a new P2P reputation system
is presented in (
Song et al., 2005) based on “Fuzzy
Logic Inferences” which can better handle
uncertainty, fuzziness, and incomplete information
in peer trust reports. They demonstrate the efficacy
and robustness of two P2P reputation systems
(FuzzyTrust and EigenTrust) at establishing trust
among the peers.
In the next section, we evaluate the behavior of
the proposed trust function in (
Yu and Singh, 2000)
and offer a new approach for the trust calculation.
3 TRUST FUNCTION
In this section, we evaluate a specific trust function
by Yu and Singh (2000) and assess its behavior. In
the proposed scheme, after an interaction the
updated trust rating T
t+1
is given by the following
formulas (Table 1) and depends on the previous
trust rating where:
α
>= 0,
β
<=0
Table 1: Trust function from (Yu and Singh, 2000).
T
t
Cooperation
> 0
T
t
+
α
(1-T
t
)
< 0
(T
t
+
α
)/(1-min{|T
t
|,|
α
|})
= 0
α
T
t
Defection
> 0
(T
t
+
β
)/(1-min{|T
t
|,|
β
|})
< 0
T
t
+
β
(1+T
t
)
= 0
β
The following diagram (Figure 2) shows the
behavior of the Yu trust function, it is convergent at
points (+1, +1) and (-1, -1). The above curve is for
the cooperation and the other one is for the
defection. This function also crosses axis Y at the
following points:
α
=0.1 and
β
=-0.2 where T
t
is
equal to zero.
A NEW APPROACH FOR THE TRUST CALCULATION IN SOCIAL NETWORKS
259

Figure 2: Yu trust function diagram (
α
=0.1 &
β
=-0.2).
3.1 Evaluation of the Yu Trust
Function
To see the exact properties of the Yu trust function,
refer to the Table 2, which shows T
t
and its
corresponding value (T
t+1
) in the interval [-1, +1].
Table 2: Trust function’s behavior,
α
=0.1 &
β
=-0.2.
T
t
Plus T
t+1
T
t
Minu
s
T
t+1
1 0 1 1 0 1
0.9 0.01 0.91 0.9 -0.03 0.87
0.8 0.02 0.82 0.8 -0.05 0.75
0.7 0.03 0.73 0.7 -0.08 0.62
0.6 0.04 0.64 0.6 -0.1 0.5
0.5 0.05 0.55 0.5 -0.13 0.37
0.4 0.06 0.46 0.4 -0.15 0.25
0.3 0.07 0.37 0.3 -0.18 0.12
0.2 0.08 0.28 0.2 -0.2 0
0.1 0.09 0.19
0.16 -0.21 -0.06
0 0.1 0.1 0.12 -0.21 -0.09
0.08 -0.21 -0.13
-0.02 0.1 0.08 0.04 -0.21 -0.17
-0.05 0.1 0.05
-0.08 0.1 0.02 0 -0.2 -0.2
-0.1 0.1 0 -0.1 -0.18 -0.28
-0.2 0.09 -0.11 -0.2 -0.16 -0.36
-0.3 0.08 -0.22 -0.3 -0.14 -0.44
-0.4 0.07 -0.33 -0.4 -0.12 -0.52
-0.5 0.06 -0.44 -0.5 -0.1 -0.6
-0.6 0.04 -0.56 -0.6 -0.08 -0.68
-0.7 0.03 -0.67 -0.7 -0.06 -0.76
-0.8 0.02 -0.78 -0.8 -0.04 -0.84
-0.9 0.01 -0.89 -0.9 -0.02 -0.92
-1 0 -1 -1 0 -1
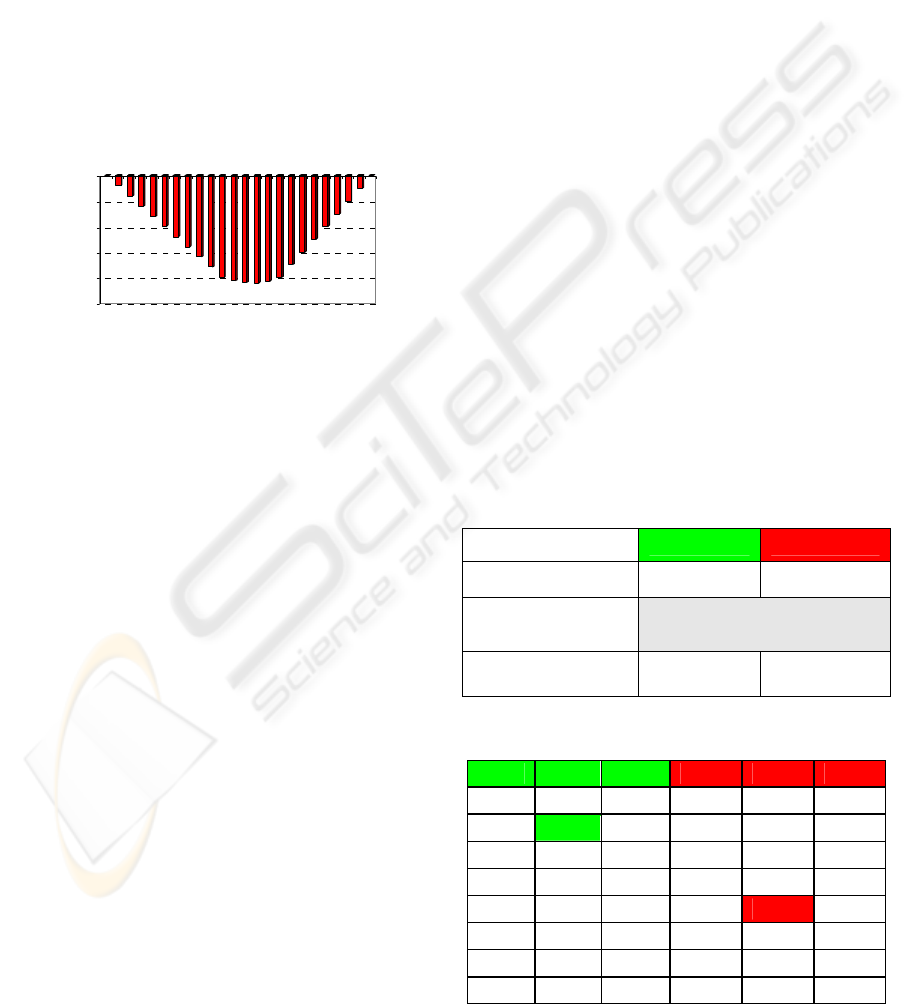
Figure 3 illustrates the behavior of the proposed
trust function in cooperation situations. It shows the
reward values in the interval [-1, +1]. The main
critique here is for cooperation in the interval (0, +1]
but the behavior of the function in the interval [-1,
0) is fine. Consider the two following scenarios for
cooperation:
a) If the participant is a trustworthy agent (e.g.
T=0.8) and shows more cooperation, the function
increases the trust value a little bit (0.02), but if it is
not very trustworthy (e.g. T=0.2) and shows
cooperation, the function enhances the trust value a
lot (0.08). These are not good properties.
b) If the participant is a corrupt agent (e.g. T=-
0.8) and shows cooperation, the function increases
the trust value a little bit (0.02) and if agent’s trust
value is e.g. T=-0.2 and shows cooperation, the
function enhances the trust value more (0.09) in
comparison to the previous situation. These are good
properties.
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
Plus
-1 -0.8 -0.6 -0.4 -0.2 -0.1 -0 0.1 0.3 0.5 0.7 0.9
Trust Value
Cooperation
Figure 3: Yu trust function’s behavior in cooperation.
Figure 4 demonstrates the behavior of the
proposed trust function in defection situations. It
shows the penalty values in the interval [-1, +1]. The
main critique here is for defection in the interval [-1,
0) but the behavior of the function in the interval (0,
+1] is fine. Consider the two following scenarios for
defection:
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
260

c) If the participant is a trustworthy agent (e.g.
T=0.8) and shows defection, the function decreases
the trust value a little bit (-0.05), but if it is not very
trustworthy (e.g. T= 0.2) and shows defection, the
function decreases the trust value a lot (-0.2) which
are good properties to some extend.
d) If the participant is a corrupt agent (e.g. T=-
0.8) and shows more defection, the function
decreases the trust value a little bit (-0.04) and if
agent’s trust value is e.g. T=-0.2 and shows
defection, the function decreases the trust value
more (-0.16) in compare to the previous state. These
are not good properties.
-0.25
-0.2
-0.15
-0.1
-0.05
0
Minus
-1 -0.7 -0.4 -0.1 0.08 0. 2 0.5 0.8
Trust Value
Defection
Figure 4: Yu trust function’s behavior in defection.
Therefore, this paper’s major critique is for
cooperation in scenario “a” and defection in
scenario “d”. They show bad behaviors of the trust
function. In the next section, a sample improved
function is provided to modify the trust calculation
for the social networks.
3.2 Modification of the Trust
Function
To modify the trust function in (Yu and Singh, 2000),
we consider six possible situations (Table 3). If trust
value is less than
β
then the agent is a bad
participant, if it is greater than
α
then the agent is a
good member of the society, otherwise ([
β
,
α
])
we can not judge the agent. We just suppose it is a
member who is looking for some opportunities. By
considering both cooperation and defection factors,
we have the following rules:
(1) If a bad agent cooperates, then we encourage
it a little bit, e.g. by the factor X
E
∈(0.01, 0.05)
(2) If we encounter with an agent who is looking
for a chance by cooperating, then we give it some
opportunities by the factor X
Give
= 0.05
(3) If a good agent cooperates, then we reward it
more than the encouragement factor:
X
R
∈
(0.05, 0.09) > X
E
∈
(0.01, 0.05)
(4) If a good agent defects, then we discourage it
a little bit, e.g. by the factor X
D
∈(-0.05, -0.01)
(5) If we encounter with an agent that we can not
judge it while it is defecting, then we deduct its
credit value by the factor X
Take
= -0.05
(6) If a bad agent defects, then we penalize it
more than the discouragement factor:
|X
P
|
∈
| (-0.09, -0.05)| > |X
D
|
∈
| (-0.05, -0.01)|
If the agent has an excellent trust value (e.g.
0.99) and shows more cooperation, we increase the
trust value in a way that it would be convergent to 1.
On the other side, if the agent has a poor trust value
(e.g. -0.99) and shows more defection, we decrease
the trust value in a way that it would be convergent
to -1. Therefore, the new trust function is also in
interval [-1, +1]. This function covers all the above
proposed rules, more detailed behaviors are
provided in Table 4.
Table 3: Six possible situations for interaction.
Trust Value Cooperation Defection
T
Bad Agent
∈
[-1,
β
)
Encourage Penalize
No Judgment:
[
β
,
α
]
Give/Take Opportunities
T
Good Agent
∈
(
α
,
+1]
Reward Discourage
Table 4: Modified trust function,
α
=0.1 &
β
=-0.1.
T
t
Plus T
t+1
T
t
Minus T
t+1
-1 0.005 -0.995
-1 0 -1
-0.9 0.01 -0.89
-0.975 -0.024 -0.999
-0.8 0.015 -0.785
-0.95 -0.047 -0.997
-0.7 0.02 -0.68
-0.925 -0.07 -0.995
-0.6 0.025 -0.575 -0.9 -0.09 -0.99
-0.5 0.03 -0.47 -0.8 -0.085 -0.885
-0.4 0.035 -0.365 -0.7 -0.08 -0.78
-0.3 0.04 -0.26 -0.6 -0.075 -0.675
A NEW APPROACH FOR THE TRUST CALCULATION IN SOCIAL NETWORKS
261

-0.2 0.045 -0.155 -0.5 -0.07 -0.57
-0.1 0.05 -0.05 -0.4 -0.065 -0.465
-0.05 0.05 0 -0.3 -0.06 -0.36
0 0.05 0.05 -0.2 -0.055 -0.255
0.05 0.05 0.1 -0.1 -0.05 -0.15
0.1 0.05 0.15 -0.05 -0.05 -0.1
0.2 0.055 0.255 0 -0.05 -0.05
0.3 0.06 0.36 0.05 -0.05 0
0.4 0.065 0.465 0.1 -0.05 0.05
0.5 0.07 0.57 0.2 -0.045 0.155
0.6 0.075 0.675 0.3 -0.04 0.26
0.7 0.08 0.78 0.4 -0.035 0.365
0.8 0.085 0.885 0.5 -0.03 0.47
0.9 0.09 0.99 0.6 -0.025 0.575
0.925 0.07 0.995
0.7 -0.02 0.68
0.95 0.047 0.997
0.8 -0.015 0.785
0.975 0.024 0.999
0.9
-0.01 0.89
1 0 1
1 -0.005 0.995
In the next section, the result of the new trust
function in different intervals with various scenarios
is illustrated; moreover, a quadratic regression is
provided in order to find a simpler approximating
formula for the new trust function.
4 RESULTS
In this part, a detailed evaluation of the new trust
function with its regression is presented. First of all
look at the Figure 5. It illustrates the behavior of the
new function in cooperation situations. This diagram
shows the value that trust function adds to the trust
value each time according to the following scheme:
[-1,
β
) Æ Encourage
[
β
,
α
] Æ Give Opportunities
(
α
, +1] Æ Reward
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
Plus
-1 -0.7 -0.4 -0.1 0.05 0.3 0.6 0.9 0.98
Trust Value
Cooperation
Figure 5: New function’s behavior in cooperation.
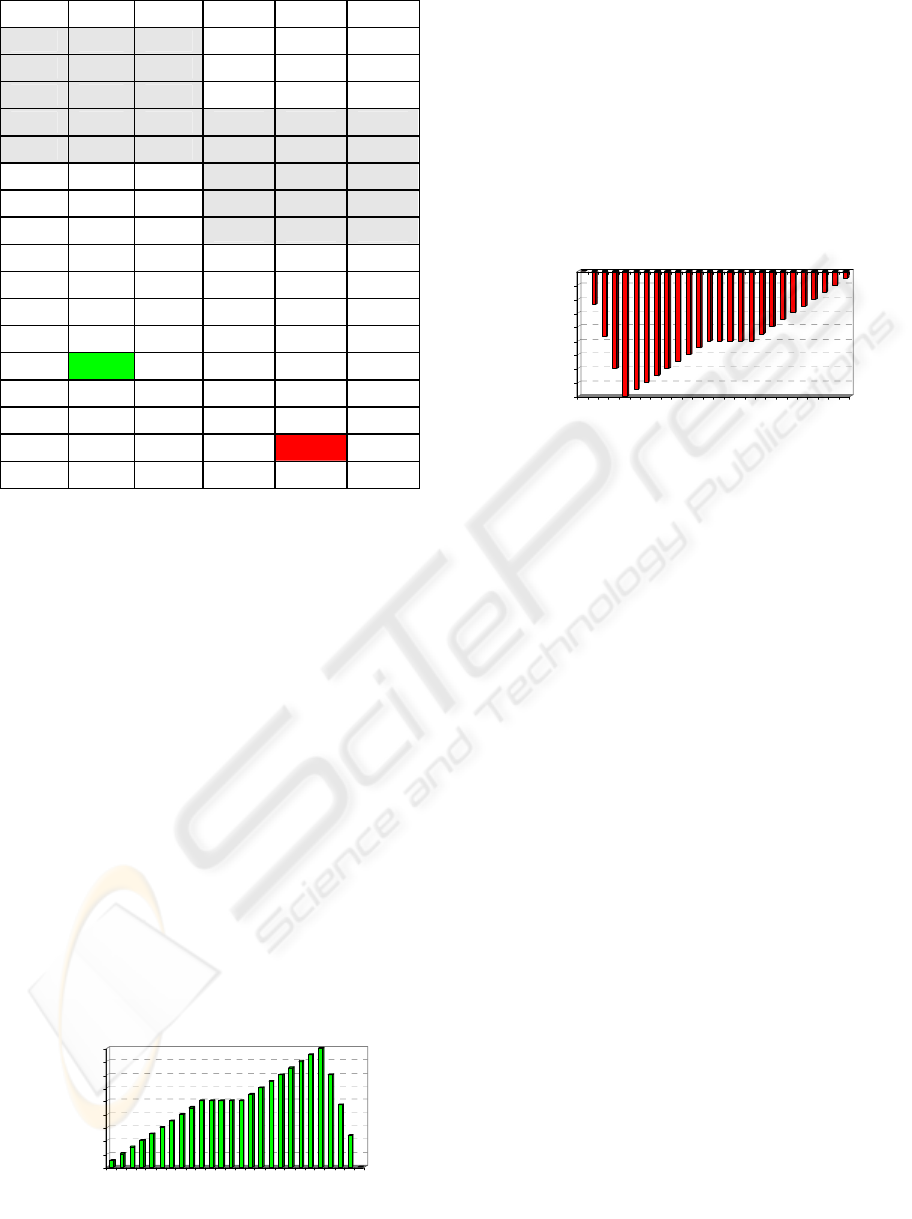
Figure 6 also illustrates the behavior of the new
function in defection situations. This diagram shows
the value that trust function deducts from the trust
value each time according to the following scheme:
[-1,
β
) Æ Penalize
[
β
,
α
] Æ Take Opportunities
(
α
, +1] Æ Discourage
-0.09
-0.08
-0.07
-0.06
-0.05
-0.04
-0.03
-0.02
-0.01
0
Minus
-1 -0.9 -0.7 -0.4 -0. 1 0.0 0. 3 0.6 0. 9
Trust Value
Defection
Figure 6: New function’s behavior in defection.
The last two diagrams show important
properties. They complete behaviors of each other.
In interval [
β
,
α
] they neutralize each other (if
β
=
α
) to provide opportunity for new agents that
their past behaviors are not available (newcomers)
and also agents who want to pass the border
between bad players and good ones. They must
prove their merit in this area; otherwise they will be
stuck in this region, because we add or deduct the
trust value with the same rate, for instance |0.05| (we
can play with
α
and
β
to change the interval, e.g.
[-0.2, +0.1]).
In interval [-1,
β
), we penalize bad agents more
than the rate that we encourage them. This means
that we try to avoid and block bad participants in
our business, at the same time we provide a chance
by interval [
β
,
α
] for the agents who want to show
their merit, if they reach this area then we behave
more benevolently.
In interval (
α
, +1], we reward good agents
more than the rate that we discourage them. This
means that we try to support good players in our
business and keep them in our trustee list as much as
we can and as long as they cooperate, although they
will be guided to the interval [
β
,
α
] if they show
bad behaviors continuously.
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
262

The other important scenario is related to the
value of the transactions, suppose a good agent
cooperates for a long time in cheap transactions (e.g.
$100) to gain a good trust value and after that he
tries to defect for some expensive transactions (e.g.
$1000). The solution is that we can consider a
coefficient (
λ
) for the value of a transaction and
then increase or decrease the trust value according to
the
λ
. For example, if the transaction value is $100
then:
λ
=1 and if it is $1000 then:
λ
=10; therefore,
if an agent cooperates for 5 times on the cheap
transactions (
λ
=1) then we add his trust value 5
times. If he defects after that on an expensive
transaction (
λ
=10) then we deduct his trust value
10 times continuously. So, by this approach we have
a more reliable trust function which depends on the
transaction value.
In Figure 7, you can see a quadratic regression
that approximates the new trust function (Table 4)
with 99.9% accuracy.
Figure 7: Quadratic regression for the new function.
The quadratic approximation to the trust function is
as follows and you can see its diagram in Figure 8:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−===
==−=
+∗+∗=
+
055.0,028.1,031.0:
055.0,028.1,031.0:
2
1
σθω
σθω
σθω
Defection
nCooperatio
TTT
ttt
Where:
T
t
∈
[-1,+1]
α
=0.1 &
β
=-0.1
X
E
∈
(0.01, 0.05)
X
Give
= 0.05
X
R
∈
(0.05, 0.09) > X
E
∈(0.01, 0.05)
X
D
∈
(-0.05, -0.01)
X
Take
= -0.05
|X
P
|
∈
|(-0.09, -0.05)| > |X
D
|∈|(-0.05, -0.01)|
Figure 8: New proposed trust function.
Above function is simpler and has better
behavior in comparison to the trust function in (
Yu
and Singh, 2000), which is more complex with some
irrational behaviors. On the other hand, this function
satisfies the proposed approach in this paper,
although we can use the cubic regression with more
sample points to achieve better accuracy. In the next
section, some discussion and concluding remarks
are provided.
5 CONCLUSION
In this paper, we evaluated a specific trust function
for social networks. The paper showed the behavior
of that function and proposed a new mathematical
approach to modify a previously published trust
A NEW APPROACH FOR THE TRUST CALCULATION IN SOCIAL NETWORKS
263

formula (Yu and Singh, 2000). A mathematical
discussion with various scenarios was provided to
demonstrate the behavior of the new trust function.
The paper used a bottom-up approach to create a
new trust function; and it provided sample points
according to the function's behavior for certain
values of 8 constants used to parameterize our
approach. We also provided a quadratic
approximation to simplify calculation of the
function, with only minor cost in accuracy.
Alternative approximations would be needed if any
of the eight constants were changed.
Another important factor is to consider both
expertise (ability to produce correct answers) and
sociability (ability to produce accurate referrals) in
social networks. Usually, the goal of a trust
function is to calculate expertise, but we should also
consider another function for the calculation of
sociability. If we do so, then we can evaluate our
social networks by those two functions. As a future
work, we would like to work on the computation of
sociability. Our purpose is to evaluate social
behaviors of agents by considering both functions at
the same time and apply a two dimensional function
for this assessment.
ACKNOWLEDGEMENTS
We appreciate the anonymous reviewers for their
comments.
REFERENCES
Yu, B. and Singh, M. P., 2000. A social mechanism of
reputation management in electronic communities. In
Proceedings of Fourth International Workshop on
Cooperative Information Agents. pages 154–165.
Marti, S. and Carcia-Molina, H., 2004. Limited reputation
sharing in P2P systems. In Proceedings of the ACM
Conference on Electronic Commerce. pages: 91-101.
Yu, B. and Singh, M. P., 2002. Distributed reputation
management for electronic commerce. Computational
Intelligence, 18 (4): 535–549.
Mui, L., 2002. Computational models of trust and
reputation”. PhD thesis in Electrical Engineering and
Computer Science, MIT.
Yu, B., Singh, M. P. and Sycara, K., 2004. Developing
trust in large-scale peer-to-peer systems. In First IEEE
Symposium on Multi-Agent Security and Survivability.
Yolum, P. and Singh, M. P., 2004. Service graphs for
building trust. In Proceedings of the International
Conference on Cooperative Information Systems, (1):
509-525.
Yu, B. and Singh, M. P., 2003. Searching social networks.
In Proceedings of the 2nd International Joint
Conference on Autonomous Agents and Multi-Agent
Systems (AAMAS), ACM Press.
Song, S., Hwang, K., Zhou, R. and kwok, Y., 2005.
Trusted P2P transactions with fuzzy reputation
aggregation. IEEE Internet Computing, 9 (6): 24-34.
Sabater, J. and Sierra, C., 2002. Reputation and social
network analysis in multi-agent systems. In
Proceedings of First International Joint Conference
on Autonomous Agents and Multi-agent Systems,
pages 475–482.
Pujol, J. M., Sanguesa, R. and Delgado, J., 2002.
Extracting reputation in multi-agent systems by means
of social network topology. In Proceedings of First
International Joint Conference on Autonomous Agents
and Multi-agent Systems, pages 467–474.
Mui, L., Mohtashemi, M. and Halberstadt, A., 2002.
Notions of reputation in multi-agents systems: a
review. In Proceedings of First International Joint
Conference on Autonomous Agents and Multi-agent
Systems, pages 280-287.
Aberer, K. and Despotovic, Z., 2001. Managing trust in a
peer-2-peer information system. In Proceedings of the
Tenth International Conference on Information and
Knowledge Management (CIKM’ 01), pages 310-317.
Breban, S. and Vassileva, J., 2001. Long-term coalitions
for the electronic marketplace. In Proceedings of
Canadian AI Workshop on Novel E-Commerce
Applications of Agents, pages 6–12.
Tan, Y. and Thoen, W., 2000. An outline of a trust model
for electronic commerce. Applied Artificial
Intelligence, 14: 849–862.
Schillo, M., Funk, P. and Rovatsos, M., 2000. Using trust
for detecting deceitful agents in artificial societies.
Applied Artificial Intelligence, 14: 825–848.
Resnick, P., Zeckhauser, R., Friedman, E., and Kuwabara,
K., 2000. Reputation systems: facilitating trust in
internet interactions. Communications of the ACM, 43
(12): 45–48.
Brainov, S. and Sandholm, T., 1999. Contracting with
uncertain level of trust. In Proceedings of the First
International Conference on Electronic Commerce
(EC’99), pages 15–21.
Rea, T. and Skevington, P., 1998. Engendering trust in
electronic commerce. British Telecommunications
Engineering, 17 (3): 150–157.
Castelfranchi, C. and Falcone, R., 1998. Principle of trust
for MAS: cognitive anatomy, social importance, and
quantification. In Proceedings of Third International
Conference on Multi Agent Systems, pages 72–79.
Chavez, A. and Maes, P., 1996. Kasbah: An agent
marketplace for buying and selling goods. In
Proceedings of the 1st International Conference on
the Practical Application of Intelligent Agents and
Multi-agent Technology (PAAM), pages 75–90.
ICE-B 2006 - INTERNATIONAL CONFERENCE ON E-BUSINESS
264