OPTIMIZED GAUSS AND CHOLESKY ALGORITHMS FOR

USING THE LMMSE DECODER IN MIMO/BLAST SYSTEMS

WITH FREQUENCY-SELECTIVE CHANNELS

Reduced-complexity Equalization

João Carlos Silva, Nuno Souto, Francisco Cercas, António Rodrigues

Instituto Superior Técnico/IT, Torre Norte 11-11, Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal

Rui Dinis, Sérgio Jesus

CAPS, Av. Rovisco Pais 1,1049-001 Lisboa, Portugal

Keywords: MMSE Equalizer, Gauss, Cholesky, MIMO, W-CDMA.

Abstract: The LMMSE (Linear Minimum Mean Square Error) algorithm is one of the best linear receivers for DS-

CDMA (Direct Sequence-Code Division Multiple Access). However, for the case of MIMO/BLAST

(Multiple Input, Multiple Output / Bell Laboratories Layered Space Time), the perceived complexity of the

LMMSE receiver is taken as too big, and thus other types of receivers are employed, yielding worse results.

In this paper, we investigate the complexity of the solution to the LMMSE and the Zero-Forcing (LMMSE

without noise estimation) receiver’s equations. It will be shown that the equation can be solved with

optimized Gauss or Cholesky algorithms. Some of those solutions are very computationally efficient and

thus, allow for the usage of the LMMSE in fully-loaded MIMO systems.

1 INTRODUCTION

Digital communication using MIMO, sometimes

called a “volume-to volume” wireless link, has

recently emerged as one of the most significant

technical breakthroughs in modern communications.

Just a few years after its invention the technology is

already part of the standards for wireless local area

networks (WLAN), third-generation (3G) networks

and beyond.

MIMO schemes are used in order to push the

capacity and throughput limits as high as possible

without an increase in spectrum bandwidth, although

there is an obvious increase in complexity. For N

transmit and M receive antennas, we have the

capacity equation (Foschini, 1998), (Telatar, 1999)

log det I '

EP M

CHH

⎛⎞

⎜⎟

⎝⎠

b/s/Hz (1)

where H is the channel matrix, H’ is the

transpose-conjugate of H and ρ is the SNR at any

receive antenna. (Foschini, 1998) and (Telatar, 1999)

both demonstrated that the capacity grows linearly

with m=min(M,N), for uncorrelated channels.

Therefore, it is possible to augment the

capacity/throughput by any factor, depending on the

number of transmit and receive antennas. The

downside to this is the receiver complexity,

sensitivity to interference and correlation between

antennas, which is more significant as the antennas

are closer together. For a 3G system, for instance, it

is inadequate to consider more than 2 or 4 antennas at

the UE (User Equipment)/ mobile receiver.

Note that, unlike in CDMA where user’s

signatures are quasi-orthogonal by design, the

separability of the MIMO channel relies on the

presence of rich multipath which is needed to make

the channel spatially selective. Therefore, MIMO can

be said to effectively exploit multipath.

The receiver for such a scheme is obviously

complex; due to the number of antennas, users and

multipath components, the performance of a simple

RAKE/ MF (Matched Filter) receiver (or enhanced

schemes based on the MF) always introduces a

200

Carlos Silva J., Souto N., Cercas F., Rodrigues A., Dinis R. and Jesus S. (2006).

OPTIMIZED GAUSS AND CHOLESKY ALGORITHMS FOR USING THE LMMSE DECODER IN MIMO/BLAST SYSTEMS WITH FREQUENCY-

SELECTIVE CHANNELS - Reduced-complexity Equalization.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 200-208

 SciTePress

significant amount of noise, that doesn’t allow for the

system to perform at full capacity. Thus being, the

LMMSE receiver was considered for such cases,

acting as an equalizer.

The structure of the paper is as follows. In

Section II, the LMMSE receiver for MIMO with

multipath is introduced. Section III presents the

proposed optimizations to the standard methods of

Gauss and Cholesky. In section IV an approximate

method based in the Cholesky way is discussed, and

conclusions are drawn in Section V.

2 LMMSE RECEIVER

A standard model for a DS-CDMA system with K

users (assuming 1 user per physical channel) and L

propagation paths is considered. The modulated

symbols are spread by a Walsh-Hadamard code with

length equal to the Spreading Factor (SF). The signal

on a MIMO-BLAST system with N

transmit and

receive antennas, at one of the receiver’s

antennas, can be expressed as:

A standard model for a DS-CDMA system with K

users (assuming 1 user per physical channel) and L

propagation paths is considered. The symbols

(QPSK/16QAM) are spread by a Walsh-Hadamard

code with length equal to the Spreading Factor (SF).

The received signal on a MIMO system with N

transmit and N

receive antennas on one of the

receiver’s antennas can be expressed as:

()

1,, ,,

111

() ( )* () ()

v RX ktx ktx k ktxrx

ntxk

rt A b s t nT c t nt

===

=−+

∑∑∑

(2)

where N is the number of received symbols,

,ktx k

, E

is the energy per symbol,

()

ktx

is the

n-th transmitted data symbol of user k and transmit

antenna tx, s

(t) is the k-th user’s signature signal

(equal for all antennas), T denotes the symbol

interval, n(t) is a complex zero-mean AWGN with

variance

()

,, ,, , ,

() ( )

ktxrx ktxrxl kl

ct c t

=−

∑

is the

impulse response of the k

th user’s radio channel,

k,tx,rx,l

is the complex attenuation factor of the k-ths

user’s l-th path of the link between the tx-th and rx-

th antenna,

,kl

is the propagation delay (assumed

equal for all antennas) and (*) denotes convolution.

The received signal on can also be expressed as:

()

1 ,,,, ,

1111

() () ( ) ()

NKL

vRX ktxktxktxrx k kl

ntxk l

rt A b c tst nT nt

====

=−−+

∑∑∑∑

(3)

Using matrix algebra,

rSCAbn=+

, where S, C and

A are the spreading, channel and amplitude matrices

respectively. The spreading matrix S has dimensions

(

)

(

)

X MAX RX RX

SF N N N K L N N

⋅⋅ + ⋅ × ⋅⋅⋅

(τ

max

the maximum delay of the channel’s impulse

response, normalized to number of chips), and is

composed of sub-matrices S

in its diagonal for

each receive antenna

RX=1 RX=N

S=diag(S , ,S )…

. Each

of these sub-matrices has dimensions

(

)

(

)

MAX

SF N K L N

⋅

+×⋅⋅

, and are further

composed by smaller matrices S

, one for each bit

position, with size

(

)

(

)

MAX

SF K L

×⋅

. The S

matrix structure is made of

( )() ( )()

RX,n n

SF ( 1) K L SF (N-n) K L

RX RX,1 RX,N

S=0 ,S,0

S=S , ,S

n⋅− × ⋅ ⋅ × ⋅

⎡

⎤

⎣

⎦

⎡⎤

⎣⎦

…

The S

matrices are made of

L⋅

columns;

n col(k=1,l=1),n col(k=1,l=L),n col(k=K,l=L),n

S=S , ,S , ,S

⎡

⎤

⎣

⎦

……

. Each

of these columns is composed of

()

col(KL),n 1

1 delay(L)

1()

S=0 , (),0

MAX

nSF

delay L

spread K

×−

⎡

⎤

⎣

⎦

where spread

(K) is the combined spreading &

scrambling for the bit n of user K.

These S

matrices are either all alike if no long

scrambling code is used, or different if the

scrambling sequence is longer than the SF. The S

matrices represent the combined spreading and

scrambling sequences, conjugated with the channel

delays. The shifted spreading vectors for the

multipath components are all equal to the original

sequence of the specific user.

1,1,1, ,1,1,

1,1, , ,1, ,

1, ,1, , ,1,

1, , , , , ,

nKn

Ln K Ln

SF n K SF n

SF L n K SF L n

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦



  

 



Note that, in order to correctly model the multipath

interference between symbols, there is an overlap

between the S

matrices, of τ

MAX

The channel matrix

C is a

(

)

(

)

RX TX

LNN KN N

⋅

⋅⋅ × ⋅ ⋅

matrix, and is

composed of RX sub-matrices, each one for a RX

antenna

1RX=N

C= C , , C

RX =

⎡

⎤

⎣

⎦

…

. The diagonals of

each C

matrix are composed of N C

matrices.

1,1

⎡

⎤

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎢

⎥

⎢

⎥

⎢

⎥

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎣

⎦







Each C

matrix is

(

)

(

)

KL KN⋅× ⋅

, and

represents the fading coefficients for each path, user

and TX antenna, for the current symbol and RX

OPTIMIZED GAUSS AND CHOLESKY ALGORITHMS FOR USING THE LMMSE DECODER IN MIMO/BLAST

SYSTEMS WITH FREQUENCY-SELECTIVE CHANNELS - Reduced-complexity Equalization

201

antenna. The matrix structure is made up of further

smaller matrices along the diagonal

(

)

KT T T

K=1 K=K

C=diagC , ,C…

, with C

of dimensions

N×

, representing the fading coefficients for the

user’s multipath and tx-th antenna component.

1,1,1 ,1,1

1, ,1 , ,1

1,1, ,1,

1, , , ,

LNL

KNK

LK N LK

⎡⎤

⎢⎥

⎣⎦















The A matrix is a diagonal matrix of

dimension

(

)

NN⋅⋅

, and represents the

amplitude of each user per transmission antenna and

symbol,

(

)

TX TX TX

1,1,1 N ,1,1 N ,K,1 N ,K,N

A=diag A , , A , , A , , A…… …

Vector

b represents the information symbols. It has

length

(

)

KN N⋅⋅

, and has the following

structure

TX TX TX

1,1,1 N ,1,1 1,K,1 N ,K,1 N ,K,N

b= b , ,b , ,b , ,b , ,b

⎡⎤

⎣⎦

……… …

Note that the bits of each TX antenna are grouped

together in the first level, and the bits of other

interferers in the second level. This is to guarantee

that the resulting matrix to be inverted has all its

non-zeros values as close to the diagonal as possible.

Also note that there is usually a higher correlation

between bits from different antennas using the same

spreading code, than between bits with different

spreading codes.

Finally, the

n vector is a

(

)

XRXMAX

NSFN N

⋅⋅ + ⋅

vector with noise components to be added to the

received vector r

, which is partitioned by N

antennas,

RX RX

v 1,1,1 1,SF,1 N,1,1 N,SF+ ,1 N,1,N N,SF+ ,N

r = R , ,R , ,R , ,R , ,R , ,R

MAX MAX

ττ

⎡⎤

⎣⎦

……… … …

The MMSE algorithm yields the symbol estimates,

MMSE

, which should be compared to vector b,

(

)

ySCArv

=⋅

(

)

MMSE MF

yEMy

MACRCA I

−

(4)

where

is the noise variance of n, y

is the

matched filter output and EM is the Equalization

Matrix (cross-correlation matrix of the users’

signature sequences after matched filtering, at the

receiver).

The expected main problem associated with such

scheme is the size of the matrices, which assume

huge proportions. Due to the multipath causing

Inter-Symbolic Interference (ISI), the whole

information block has to be simulated at once,

requiring the use of a significant amount of memory

and some computing power for the algebraic

operations, with emphasis on the inversion of the

EM in the MMSE algorithm.

Matrix Reordering

Matrix reordering is used in order to simplify the

solving of the MMSE equation. While in the original

version the

SCA matrix is devised in such a way as

to make the received vector is divided per receive

antenna in order to make the system matrices more

perceivable, the reordering of the structure of the

SCA matrix is done solely to simplify processing.

Replacing:

()

reord=TSCA

;

=NI

;

MSE

=dy

and ()

reord

er in the MMSE

equation we obtain a simpler version:



()

HH−

TT N Te

where

(

)

reord x

represents a line-reordering of

vector or matrix

x where the lines of each antenna

were intercalated with the propose of making a more

compact and almost block-circulant matrix.

()

(1, :)

(,:)

TX N

reord

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦



(6)

Figure 1(a) shows the reordering result for a two

antennas matrix. For high SNRs equation (5)

becomes the Zero-Forcing detector equation:



()

HH−

=dTTTe (7)

Since usually

MAX

≤

, the

TT product

results in a square matrix with the structure

presented in Figure 1(b) with:

aKN= and

nKNN

. It can be shown that

TTis a

positive definite Hermitian matrix. Earlier works

(Vollmer, 2001), (Machauer, 2001), dealt only with

the Zero-Forcing detector equation for constant

channel situations. Here the validity of those

algorithms for unsteady channels situations will be

evaluated. New algorithms for unsteady channel

situations will be proposed and some optimizations

will be also introduced and presented in pseudo-code

form. Finally, all the algorithms will be adapted to

the LMMSE detector.

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

202

Figure 1: Line reordering sample for N

= 2.

Figure 2: Typical correlation matrix.

Figure 3: Generalized equalization matrix.

Figure 4: Optimized Gauss algorithm.

3 GAUSS AND CHOLESKI

ALGORITHMS

Equation (7) can be written as an Ax=b system with

A being a positive definite Hermitian matrix, where

TT,



d and

b = Te. It can be solved

for

x using the Gauss elimination or the Cholesky

algorithm.

We are interested in solving the

Ax=b system for a

particular

b vector only, so there is no need to invert

the

A matrix. The Gauss elimination can be used to

transform the

Ax=b system in a Ux=b’ where U is an

upper triangular matrix and then

x can be obtained

by direct substitution. The Cholesky method is a

little bit more complex: first

A is factorized in

A=U

U by the Cholesky algorithm, then U

Ux=b

can be decomposed in

c=b and Ux=c; these two

systems can be solved by direct substitution. The

Cholesky algorithm can save almost half of the

floating point operations needed in the Gauss

elimination because it takes advantage of the

symmetry of the

A matrix, but the Gauss elimination

is less complex and requires no square roots to be

calculated. Previous works (Noguet, 2004) have

successfully designed and implemented a real-time

hardware structure of the regular Cholesky

algorithm for the ZF joint-detection algorithm in the

UMTS/TDD context based on a SIMD structure

(Flynn, 1972) (systolic array). With the algorithms

presented in this paper a significant complexity

reduction can be expected, thereby reducing by a

great amount the size of the hardware structure,

alongside the cost and processing time. Table 1(a)

shows the number of floating point operations

required by both methods. The additions are

separated into real and complex (R+ and C+,

respectively). The extra operations wasted by the

Gauss algorithm are partially recovered in the

substitution phase, where the Cholesky method

requires the solution of two triangular systems and

hence twice the operations of the Gauss algorithm.

The number of operations required in this phase is

also included in Table 1(a).

The Order column presents the highest power of the

total number of operations considering each

multiplication-addition pair as a single operation.

Table 1: Number of floating operations needed to solve

the Ax=b system with standard Gauss algorithm.

OPTIMIZED GAUSS AND CHOLESKY ALGORITHMS FOR USING THE LMMSE DECODER IN MIMO/BLAST

SYSTEMS WITH FREQUENCY-SELECTIVE CHANNELS - Reduced-complexity Equalization

203

Table 2: Number of floating operations needed to solve

the Ax=b system with optimized Gauss algorithm.

Table 3: Number of floating operations needed to solve

the Ax=b system with optimized Cholesky algorithm.

Table 4: Number of floating operations needed to solve

the Ax=b system with optimized Cholesky algorithm;

special case when

/2ba=

Optimizations

A generic positive definite Hermitian matrix that is

nonzero only in equally overlapped squares centred

along the diagonal is represented in Figure 1(c). The

number of overlapped squares is

−

. The

Gauss algorithm can be optimized for this type of

matrix by eliminating the operations involving zero

elements. The idea is presented in Figure 1(d). First,

the standard Gauss algorithm is applied to the r1

square sub-matrix. There is no need to change the r4

rectangle. Next step is the elimination of the r2

block using the last a-b pivots of r1 (the pivots are

the diagonal elements after the elimination phase).

During this phase r3 is updated. Finally the

standard algorithm is applied to r3. This process is

repeated until all blocks are updated. During this

process, as each line is updated, the correspondent

element of vector

b is simultaneously updated. Note

that the matrix diagonal is fully contained in the

diagonal squares.

Table 1(b) presents the number of floating point

operations required in each of the tree phases

described. The total number of operations can be

calculated from:

(

)

123

(1)

Gauss Opt Gauss r Gauss r Gauss r

NNdNN=+− +

(8)

Leading to:

1()

22 2

Gauss Opt

baab

Nna

−

⎛⎞

=−−−

⎜⎟

⎝⎠

(9)

()

32 2

32 3

91816 1

928916

48 48

Gauss Opt Gauss Opt

aabb

aab b

×+

−+ −

−++

=−

(10)

A similar adaptation can be developed for the

Cholesky factorization algorithm. We will optimize

the column-Cholesky algorithm (presented in Figure

5) although similar results could be achieved for the

line version of that algorithm. Figure 6(a) sketches

such approach. In this case only the upper triangle

has to be accessed. First, the standard column-

Cholesky algorithm is applied to the r1 triangle. In a

second step the rectangle r2 is calculated accessing

only the elements of r2 and r1. In the next step, the

triangle r3 is computed using only elements of r2

and r3. Last two steps are repeated for all remaining

blocks, using always only elements of the last and

current block. As in the optimized Gauss algorithm,

the rectangular blocks do not contain the diagonal.

Table 1(c) presents the number of floating point

operations of the tree phases described. The total

number of operations can be calculated from:

(

)

123

(1)

Chol Opt Chol r Chol r Chol r

NNdNN=+− +

(11)

Leading to:

1()

22 2

Chol Opt

baab

Nna

−

⎛⎞

=−−−

⎜⎟

⎝⎠

(12)

()

22 2

2(2)1

22 6 6 32 6

Chol Opt

aa b aa b

Nn b ba bb

⎛⎞⎛

⎞

⎛⎞

=−+++−−−+++

⎜⎟⎜

⎟

⎜⎟

⎝⎠

⎝⎠⎝

⎠

(13)

()

22 2

2(1)

22 623 32 62

Chol Opt

aa bb aa b

Nn b a bb

⎛⎞⎛

⎞

⎛⎞

= − + + ++ − − ++ +

⎜⎟⎜

⎟

⎜⎟

⎝⎠

⎝⎠⎝

⎠

(14)

()

22 2

Chol Opt

na b a

⎛⎞

−+ + −

⎜⎟

⎝⎠

(15)

Chol Opt

(16)

Figure 5: Column oriented Cholesky factorization.

Both Gauss and Cholesky methods need final

substitution phases. These substitutions can also be

optimized since the resulting matrices have a

structure similar to the original

A matrix but with

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

204

nonzero elements only above (or below) the

diagonal, like shown in Figure 6(b).

The solution of a system

Ax=b with A having a

structure similar to the structure presented in Figure

6(b) requires one division for each line of the matrix

and one pair multiplication-addition for each

nonzero element. Since there are

()

dad ab

⎛⎞

−

⎛⎞

⎜⎟

−−− −−

⎜⎟

⎝⎠

(17)

nonzero elements, the number of floating point

operations needed can be written:

Subs Opt

(18)

()

Subs Opt Subs Opt

aa b

NNna

×+

−

⎛⎞

==−−−

⎜⎟

⎝⎠

(19)

We are interested in a special type of block-diagonal

positive definite Hermitian matrices, with

/2ba

like represented in Figure 6(b). Re-writing the above

equations for this special case and keeping only the

n-dependent terms (

na>>

), results in Table 1(d) As

can be seen, the optimized Cholesky algorithm can

save almost 30% of the number of operations

required for the optimized Gauss algorithm, despite

it increased complexity and need of square root

operations.

Figure 6: (a) Optimized Cholesky algorithm, (b) Gauss

elimination / Cholesky factorization resulting matrix

structure.

Partitioning

Partitioning the block-diagonal system Ax=b would

be very useful to reduce the number of floating point

operations needed to solve the system (if no overlap

is used; i.e., in good channel conditions) and also

could permit the introduction of parallelism is

algorithms that are intrinsically sequential, like the

algorithms presented in previous sections. In this

section we will discuss different partitioning

approaches.

Since A is block-diagonal and has generally

decreasing values as we get farther from its

diagonal, it is expected that it can be divided in

smaller matrices that produce smaller systems whose

combined solutions would approximate the solution

of the original system. Figure 7(a) presents a sample

solution of a system simply divided in 2 sub-systems

as sketched in Figure 8(a). Note that there are two

m × m blocks completely ignored at the middle of

the A matrix. Surprisingly the obtained maximum

error is only 12% of the exact solution. Figure 7(b)

shows the same data when the

A matrix is divided in

four slices. The maximum error level is

approximately the same as in the previous case, but

now we have three high error regions.

Although the error obtained with the last partitioning

method is not extremely high and appear only

around the division lines, much better results can be

attained if overlapping partitions are considered.

This proceeding is sketched in Figure 8(b). Each

slice overlaps the last in 2 × lap blocks (a lap being

the number of blocks that are discarded from each

overlapping side of each computed slice). Note that

the last slice can be smaller.

From each slice are obtained

(2)Dlapm−

values for

the solution vector x, except in the case of the first

and last slices, where

()Dlapm−

and

(( 1) )

LDlapm

−

−+

values are obtained

respectively.

As seen in Figure 7(a) and (c), the error level rises at

the beginning and end of each slice, so the

overlapping method should discard that values. In

each iteration are discarded lap × m values from the

beginning and lap × m values from the end, except

in the first end last slice, where are only discarded

the last lap × m and first lap × m values respectively.

Figure 7: Relative error obtained solving a no-overlap

partitioned system. (a) - M=192; m=12; D=8; v=10Km/h,

(b) - M=192; m=12; D=4; v=10Km/h.

OPTIMIZED GAUSS AND CHOLESKY ALGORITHMS FOR USING THE LMMSE DECODER IN MIMO/BLAST

SYSTEMS WITH FREQUENCY-SELECTIVE CHANNELS - Reduced-complexity Equalization

205

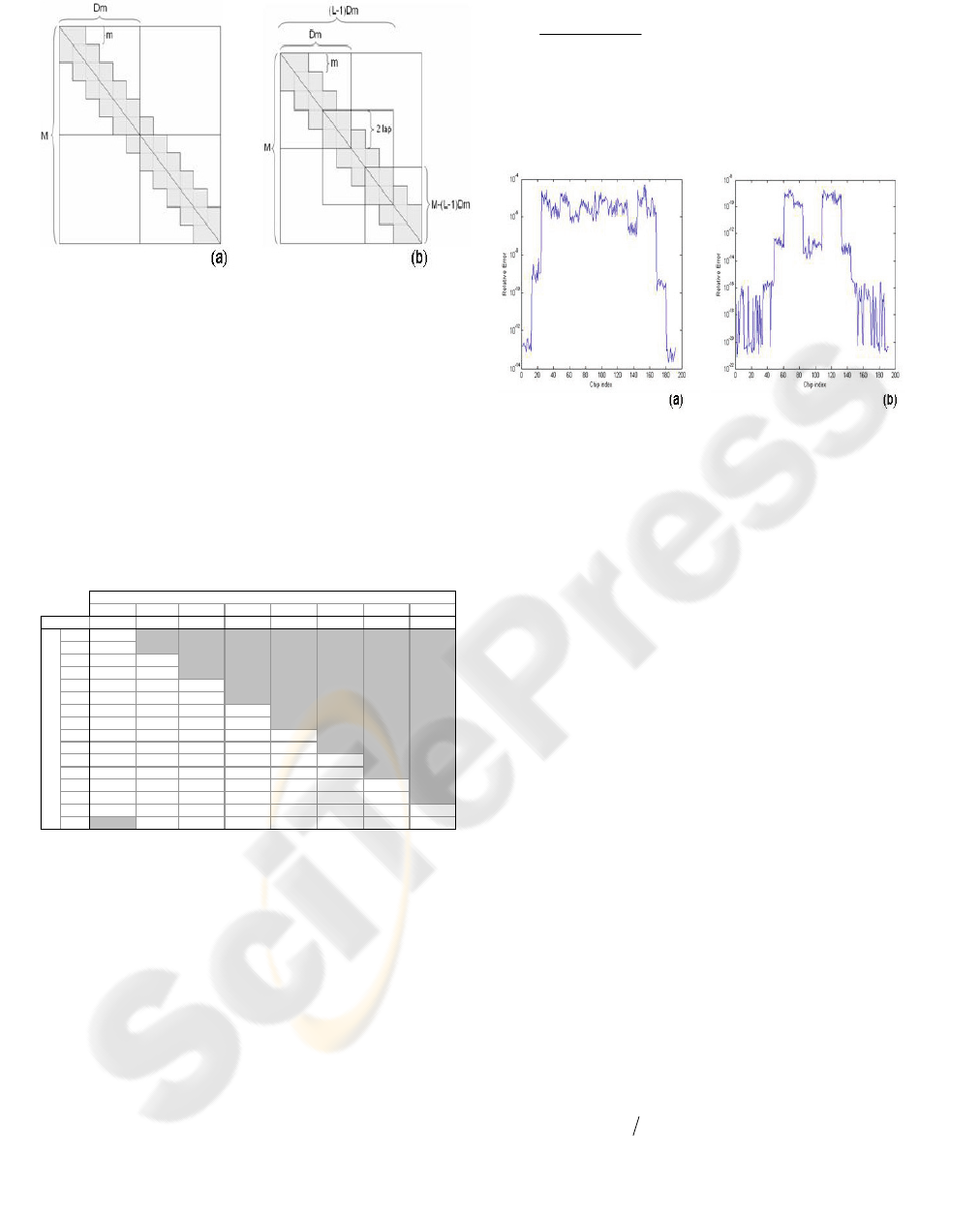
Figure 8: Partitioning (a) - without overlapping, (b) – with

overlapping.

An alternative to have a final slice with size smaller

than the early ones is to extend the b vector with

zeros until

mlap−

becomes multiple

2Dlap−

. Several simulations were run for

different channel changing speeds. Similar results

were obtained for all matrices tested. Sample results

are presented in Table 2, for a 10Km/h condition.

Table 5: Maximum relative error for the partitioning

algorithm; v=10Km/h.

01234567

1.E+00 1.E-04 1.E-07 1.E-11 1.E-15 1.E-15 1.E-15 1.E-15

1 0.506

2 0.459

3 0.152 0.911

4 0.221 0.494

5 0.127 0.494 0.090

6 0.082 0.494 0.123

7 0.459 0.105 0.123 0.247

8 0.221 0.494 0.021 0.063

9 0.083 0.640 0.042 0.038 0.898

10 0.099 0.194 0.123 0.063 0.637

11 0.079 0.190 0.037 0.222 0.817 0.505

12 0.033 0.082 0.020 0.038 0.646 0.623

13 0.159 0.059 0.015 0.036 0.642 0.552 0.416

14 0.459 0.494 0.018 0.047 0.572 0.432 0.504

15 0.127 0.845 0.090 0.033 0.420 0.284 0.252 0.378

16 0.009 0.005 0.006 0.479 0.232 0.432 0.504

Factor:

lap

All the values presented should be multiplied by the

corresponding column factor to obtain the maximum

error of the partition algorithm relative to the exact

solution of the original Ax=b system. The column

for lap=0 corresponds to the lap less situation.

shows that the maximum error level depends almost

exclusively from the overlapping level, so the proper

overlapping can be easily selected just by knowing

the maximum error allowed in the real system. The

number of blocks D processed by each thread can be

selected from the total number of threads L that can

be executed simultaneously by the hardware, using

the relation:

mlap

Dlap

⎡

⎤

−

⎢

⎥

−

⎢

⎥

, (20)

where

⎡

⎤

⎢

⎥

represents the smallest integer greater

than or equal to x. Some results of the relative error

obtained in an overlap system are portrayed in

Figure 9.

Figure 9: Relative error obtained solving an overlap

partitioned system (a) - D=4; lap=1; v=10Km/h, (b) - D=8;

lap=2; v=10Km/h.

4 PARTIAL CHOLESKI

APPROXIMATION

The Cholesky decomposition of block-Toeplitz

matrices is an upper (or lower) matrix approximately

block-Toeplitz with the same block size as the

original matrix. This means that the U matrix can be

approximated calculating only the first L block-rows

and assuming that the remaining block-rows are

identical to the last calculated block-row. Figure 7

shows this approach. Only the dark shaded part is

computed. The last computed block (marked as L) is

then repeated until the full matrix is completed. This

approximation is very effective when the channel is

constant.

Figure 8 shows the maximum relative error of the

system solution for each approximation level (L) i.e.

the number of calculated blocks, for different speeds

in a pedestrian A condition with 1 antenna.

As can be seen for a constant channel, calculating

only the first one or two blocks allows

approximations in the system solution with relative

error below 10

-4

or 10

-9

. This can be used to greatly

reduce the number of operations necessary to solve

the system. If only 2 blocks are calculated the

number of operations can be reduced approximately

by a factor of

. However, when the channel

changes, this approach can not be used regarding to

the high error level obtained (unless the channel

change is very slow).

WINSYS 2006 - INTERNATIONAL CONFERENCE ON WIRELESS INFORMATION NETWORKS AND SYSTEMS

206

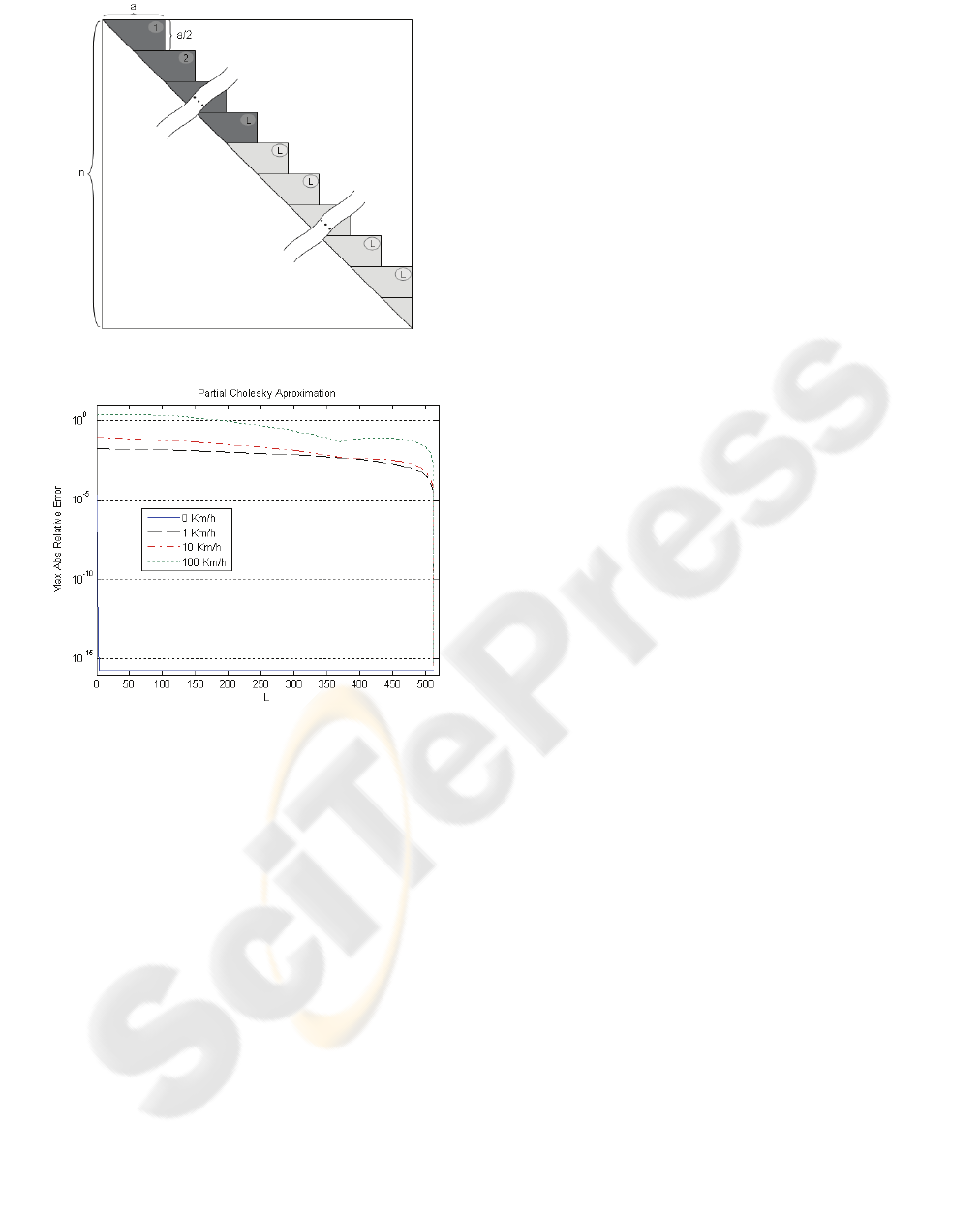
Figure 10: Partial Cholesky approximation.

Figure 11: Partial Cholesky approximation; (pedestrianA –

minimum load).

5 CONCLUSIONS

In this work where presented optimized versions of

the Gauss and Cholesky algorithms that can be used

in the solution of the equation of a zero-forcing or

LMMSE detector in MIMO/BLAST systems. Those

optimizations were based simply in the removal of

the unnecessary operations regarding the structure of

the involved matrices. It has the advantage of being

a velocity independent solution, unlike other

methods such as the Block-Fourier (Vollmer, 2001),

(Machauer, 2001). The benefit of parallel processing

can also be exploited for these methods, with the

introduction of partitioning.

ACKNOWLEDGEMENTS

This work has been partially funded by the C-

MOBILE (Advanced MBMS for the Future Mobile

World) project, and by a grant of the Portuguese

Science and Technology Foundation (FCT).

REFERENCES

G. J. Foschini and M. J. Gans, “On limits of wireless

communications in a fading environment when using

multiple antennas,” Wireless Pers. Commun., vol. 6,

pp. 311–335, Mar. 1998.

I. E. Telatar, “Capacity of multiantenna Gaussian

channels,” Eur. Trans. Commun., vol. 10, no. 6, pp.

585–595, 1999.

M. Vollmer, M. Haardt, J. Gotze, “Comparative Study of

Joint-Detection Techniques for TD-CDMA Based

Mobile Radio Systems”, IEEE Sel. Areas Comm.,

vol.19, no.8, August 2001.

R. Machauer, M. Iurascu, F. Jondral, “FFT Speed

Multiuser Detection for High Rate Data Mode in

UTRA-FDD”, IEEE VTS 54th, vol.1, 2001.

D. Noguet, “A reconfigurable systolic architecture for

UMTS/TDD joint detection real time computation”,

ISSSTA 2004, Sydney, Australia, 30 August-2

September 2004.

M. Flynn, “Some computer organizations and their

effectiveness”, IEEE Transactions on Computers, vol

c-21, 1972.

OPTIMIZED GAUSS AND CHOLESKY ALGORITHMS FOR USING THE LMMSE DECODER IN MIMO/BLAST

SYSTEMS WITH FREQUENCY-SELECTIVE CHANNELS - Reduced-complexity Equalization

207