EVALUATION OF AN ORTHOGONAL SFBC CHANNEL

ESTIMATION SCHEME FOR MIMO OFDM WIRELESS SYSTEMS

A. D. Marousis, P. Constantinou

Mobile Radio Communications Laboratory

School of Electrical and Computer Engineering,

National Technical University of Athens, Greece

Keywords:

MIMO transceivers, channel estimation and tracking, OFDM, space-frequency block coding, link level evalu-

ation.

Abstract:

This paper presents the design and evaluation of a channel estimation scheme that is efﬁcient by means of both

the mean square error (MSE) of channel estimation/tracking and its incorporation in a real MIMO system. The

evaluation has been performed over the spatial channel model developed for MIMO simulations according to

802.16e case of 3GPP.25.996, taking also into account all IF and RF stages in the communication chain.

Orthogonality has been applied in space-frequency dimension for both preamble and pilot symbols, as well

as for the data symbols, with the application of Alamouti’s scheme. In 4G multicarrier systems that use

space-time-frequency coding, orthogonal design turns into a key factor for the performance of the system

since the channel has to remain about constant during the transmission of one orthogonal block, something

which becomes quite challenging in highly time-variant propagation channels. Furthermore, space-frequency

block coding (SFBC) becomes more efﬁcient as the number of subcarriers increases (802.16e, 802.20, etc).

The modiﬁed channel estimation scheme applied to MIMO transceiver is also efﬁcient in minimization of

the processing requirements at the receiver side by estimating only those channel properties that have been

changed assuming that the general channel conditions (low/high mobility) are known. The results presented

refer to the normalized MSE of the channel estimator and the overall performance evaluation (BER) of the

system in various propagations channels, data rates and forward error correction modes.

1 INTRODUCTION

Wireless broadband systems have to support services

that demand information transmission with very high

data rates over the wireless propagation medium. It

has been proven (Adjoudani et al., 2003) that the use

of multiple antenna elements at both ends of a wire-

less link offers both capacity gain and improvement

of robustness and reliability. Therefore, multiple in-

put multiple output (MIMO) architecture has been

incorporated in the development of various wireless

systems operating in challenging propagation envi-

ronments. In addition, the various sources of diver-

sity should be properly exploited by means of cod-

ing and transmission scheme (Tarokh et al., 1998).

Temporal diversity is realized through FEC schemes

(scrambling, Reed-Solomon, convolution, interleav-

ing). Frequency diversity is exploited by orthogo-

nal frequency division multiple (OFDM) access sys-

tems and spatial diversity is obtained by multiple an-

tennas. Furthermore, the above diversity options are

combined in space-time, space-frequency, or space-

time-frequency codes where the orthogonal property

and the ability to be preserved through the propaga-

tion channel is a key factor in the total system perfor-

mance.

Optimum space-frequency coding schemes that max-

imize the diversity gain have been proposed in

(Bolcskei and Paulraj, 2001), but the processing re-

quirements at the receiver are quite high. Space-time

block codes proposed by Alamouti and extended in

(Tarokh et al., 1999), provide a simple transmit di-

versity scheme with maximum diversity in ﬂat fad-

ing MIMO channels, which are assumed about con-

stant during the transmission of one orthogonal block.

OFDM provides ﬂat fading channel for each sub-

carrier, making space-time block codes well suited

for OFDM systems assuming that the channel coef-

ﬁcients remain constant during two or more consecu-

tive OFDM symbols.

In propagation environments with high Doppler shift

loss of orthogonality, that is assembled in space-time

domain, becomes possible, whilst in space-frequency

structure the orthogonal design is not distorted. Fur-

thermore, as the number of subcarriers increases, for

a given total bandwidth of transmission, the prob-

D. Marousis A. and Constantinou P. (2006).

EVALUATION OF AN ORTHOGONAL SFBC CHANNEL ESTIMATION SCHEME FOR MIMO OFDM WIRELESS SYSTEMS.

In Proceedings of the Inter national Conference on Wireless Information Networks and Systems, pages 13-18

 SciTePress

ability of non constant affected neighbor subcarri-

ers in severe frequency selective channels becomes

quite small. Also, the greater number of subcarriers

(WiMAX vs WiFi), the larger range is achieved, since

larger delay spreads are tolerated (up to 10 times for

WiMAX with respect to WiFi).

Channel estimation is a crucial design parameter in

the performance of a real system since it has to

estimate, track and compensate all channel distor-

tions as well as the distortions caused in RF stages

in transmitter and receiver units. Especially, in a

MIMO-OFDM system the channel distortion is de-

scribed by a complex factor per subcarrier requir-

ing from the estimator (N

sy m

· N

· M

) es-

timations/compensations per frame (N

sy m

=number

of OFDM symbols, N

=number of subcarriers per

OFDM symbol, M

=number of transmit antennas,

=number of receive antennas). Such an operation

can be particularly demanding in terms of computa-

tional effort (Li et al., 1999). Following the design of

space-frequency orthogonality also for the preamble

and pilot transmission the proposed approach causes a

pilot overhead of 3.12% per OFDM symbol in which

only phase estimation is used for the pilots that have

been carefully placed in predeﬁned positions.

In this paper, initially (section 2) the system model

is depicted giving a detailed insight of transceiver ar-

chitecture, as well as the channel models used for

the evaluation. In section 3, the channel estimation

is described giving rise to all advantages and trade

offs caused by the low computational complexity at

the receiver side. Finally (section 4), evaluation re-

sults of the channel estimation (MSE) and the over-

all system performance (BER) are given for 2x1 and

2x2 cases evaluated in various propagation models

according to 802.16e (Mobile Broadband Wireless

Access, MBWA) case of 3GPP.25.996 (3GPP, 2003-

2009) using various FEC codes and mapping formats

following the 802.16-2004 standard.

2 SYSTEM ARCHITECTURE

2.1 Transmission Scheme

The MIMO-OFDM transmitter with two branches

employing space-frequency block coding (SFBC) is

shown in ﬁg.1. A binary data block D[k] of k

bits is scrambled, encoded by a concatenated Reed-

Solomon and Convolutional encoder, followed by a

puncturer and an interleaver. The resultant bit stream

is mapped using a set of predeﬁned constellation di-

agrams (BPSK-1/2, QPSK-1/2, QPSK-3/4, 16QAM-

1/2, 16QAM-3/4, 64QAM-2/3, and 64QAM-3/4) giv-

ing a symbol stream S[m] of m symbols. The same

procedure is followed as well as for the frame control

header (FCH) (IEEE, 2004) with ﬁxed QPSK map-

ping. These symbol streams are then frequency mul-

tiplexed with 8 pilot symbols and the output is SFB

coded based on Alamouti’s scheme. The output sym-

bols are packetized in blocks of 200 symbols, zero

padded and inserted in a 256-IFFT OFDM modula-

tor. Subsequently, the outputs are time multiplexed

with the OFDM output of the SFB coded preamble

symbols P . The produced digital signals at the two

chains are converted to analog ones and up-converted

to the carrier frequency through RF stages with com-

mon oscillator. Hence, time synchronization and fre-

quency offset compensation at the receiver are exactly

the same as in the case of a SISO system.

Figure 1: Transmitter Block Diagram.

2.2 Reception Scheme

At the receiver an equivalent procedure is followed.

Alamouti’s encoding scheme (Alamouti, 1998) (ap-

plied on a basis of 2 neighbor subcarriers) offers a

simple combining scheme assuming that the channel

estimates are available. Hence, extra attention has

been paid in the channel estimation stage as shown in

ﬁg.2 (in which only one part of the 2 × 2 system has

been depicted). The received signal at the frequency

domain, either for data symbol stream, or for pream-

ble symbol stream at the receiver chain is expressed

as follows:

)

j=1

· S

(j)

+ N

(1)

where i corresponds to the subcarrier index at the

-th receive antenna, j corresponds to the trans-

mitter antenna index out of M

transmit antennas

= 2), N

corresponds to additive complex

Gaussian noise per subcarrier i with zero mean and

variance σ

. Also, H

corresponds to the chan-

nel coefﬁcient between the j-th transmit antenna and

the m

-th receive antenna for the i-th subcarrier (Stu-

ber et al., 2004). The combiner outputs are fed to

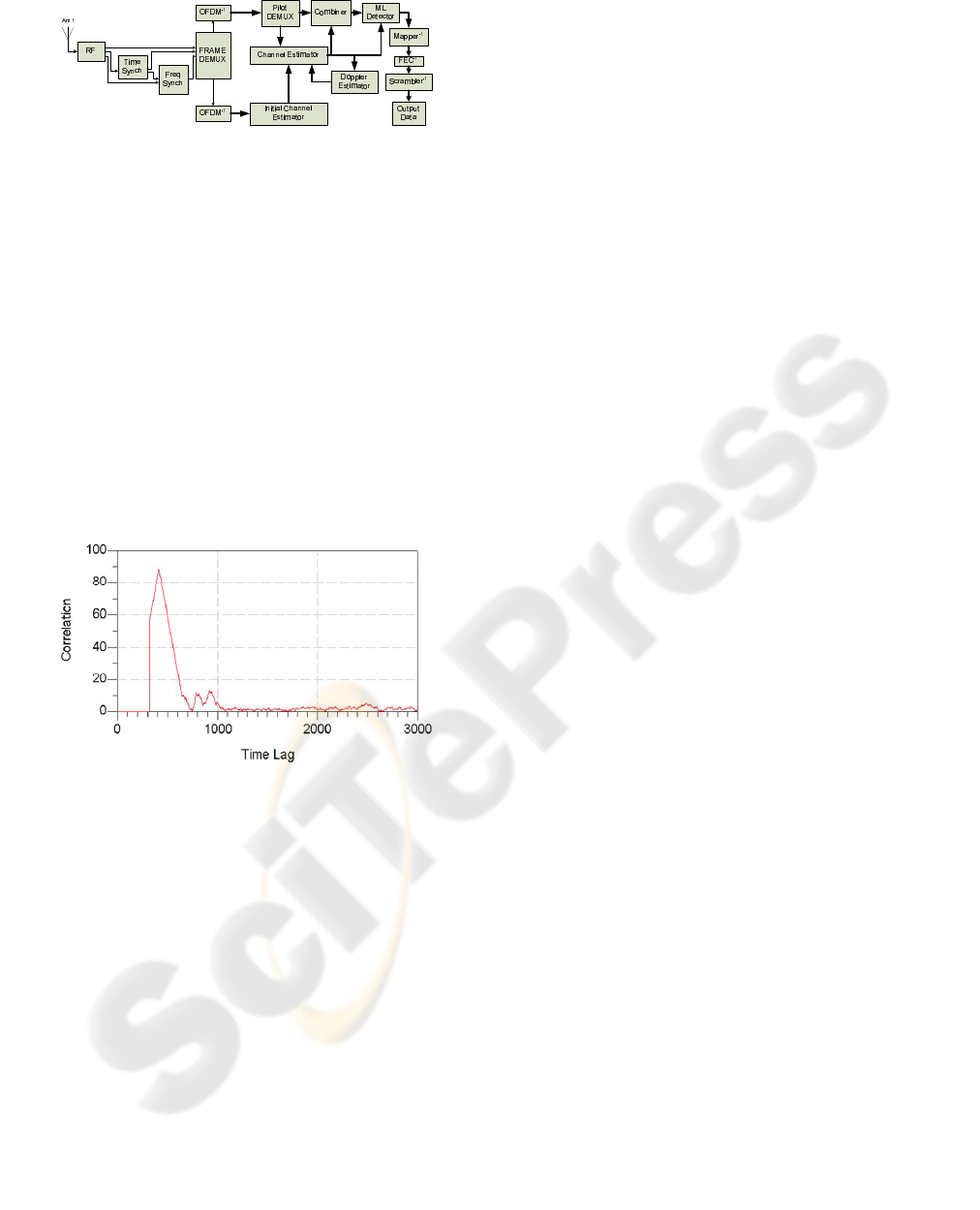
Figure 2: Receiver Block Diagram.

the maximum likelihood (ML) detector which esti-

mates the most probable symbol stream according to

the equation:

J = arg min

εC

−1

k=1



−

H · S



(2)

where C = [S

, S

, , S

N−1

]. Time and frequency

synchronization are performed based on the time-

correlation properties of the relative preamble (ﬁg.3).

The correction factor is fed back to the oscillator caus-

ing a delay. During this session, the analog automatic

gain control (AGC) is adapted and remains constant

during the subsequent frame period.

Figure 3: Correlation of time synchronization preamble at

the receiver.

2.3 Channel Models

The evaluation of SFBC MIMO-OFDM scheme has

been performed over realistic conditions taking into

account not only the channel propagation character-

istics, like time variability (Doppler shift) and multi-

path propagation (frequency selectivity), but also the

correlations between the antennas at the transmitter

and the receiver (described by Tx and Rx correla-

tion matrices). The physical parameters used for link

level modelling have been based on pedestrian level

of mobility with line of sight (Rice factor K=6dB) ac-

cording to the relative standard. Also, the proposed

correlation values have been taken into account for

an inter-element spacing of λ/2, where λ denotes the

wavelength.

3 CHANNEL ESTIMATION

Channel state information (CSI) is acquired by the re-

ceiver on a two-step procedure (ﬁg.2) whereas no CSI

is fed back to the transmitter, establishing an open-

loop system with equal transmission power on the an-

tennas. The ﬁrst step in the channel estimation pro-

cedure employs the OFDM preamble symbols which

are orthogonal on a SFBC subcarrier basis. The es-

timation has been implemented using a MMSE ap-

proach. In the second step, the pilot symbols are

used only for the phase estimation compensating the

Doppler distortion. Then, using interpolation the cor-

rection factor for each subcarrier is taken into account

in the preamble based estimation. The ﬁnal channel

estimates are used for both channel compensation and

soft decision stages. Furthermore, Doppler estimation

gives a ﬁgure of merit of the channel’s time variation

which can be potentially used to increase the num-

ber of pilot data in time dimension or for adapting a

higher order interpolation ﬁlter.

The MIMO channel estimation problem can be de-

composed into several MISO channel estimations in

parallel (Stuber et al., 2004). The initial channel es-

timation is based on the preamble OFDM symbols

that have been transmitted from the 2 antennas in an

orthogonal space-frequency format. Taking into ac-

count only the adjacent subcarriers i and i + 1 that

convey pilot information in an orthogonal format it

will be:

(1)

= H

(11)

· S

(1)

+ H

(12)

· S

(2)

(1)

i+1

= H

(11)

i+1

· S

(1)

i+1

+ H

(12)

i+1

· S

(2)

i+1

(2)

= H

(21)

· S

(1)

+ H

(22)

· S

(2)

i+1

= H

(21)

i+1

· S

(1)

i+1

+ H

(22)

i+1

· S

(2)

i+1

(3)

where R

)

is the received signal at m

-th receive

antenna in i-th subcarrier, H

)

is the channel

coefﬁcient from the m

-th transmit antenna to m

th receive antenna in i-th subcarrier, and S

)

is the

transmitted symbol from m

-th antenna in i-th sub-

carrier. Since, the Alamouti scheme has been adapted

in space-frequency dimension the transmitted sym-

bols in i-th and (i + 1)-th subcarriers will be: P

(1)

, P

∗

= S

i+1

(1)

, P

= S

(2)

, −P

∗

= S

i+1

(2)

where (·)

∗

denotes the complex conjugate operation.

In addition, the channel is assumed constant for the

subcarriers i and i + 1 giving:

(11)

= H

(11)

i+1

= H

(11)

, H

(21)

= H

(21)

i+1

= H

(21)

(12)

= H

(12)

i+1

= H

(12)

, H

(22)

= H

(22)

i+1

= H

(2)

(4)

Hence, eq.3 becomes:

(1)

= H

(11)

· P

+ H

(12)

· P

(1)

i+1

= H

(11)

· P

∗

− H

(12)

· P

∗

(2)

= H

(21)

· P

+ H

(22)

· P

(2)

i+1

= H

(21)

· P

∗

− H

(22)

· P

∗











⇒

(1)

= H

(11)

· P

+ H

(12)

· P

(1)

∗

i+1

= H

(11)

∗

· P

− H

(12)

∗

· P

(2)

= H

(21)

· P

+ H

(22)

· P

(2)

∗

i+1

= H

(21)

∗

· P

− H

(22)

∗

· P

(5)

Expressing the above formula in matrix notation, it

will be:







(1)

∗

i+1

(2)

∗

i+1













(11)

(12)

(11)

∗

−H

(12)

∗

(21)

(22)

(21)

∗

−H

(22)

∗











⇔ R

= H

· S

(6)

where the index p denotes the processed nature of the

relative receive vector and the channel matrix. The

matrix H

has unitary properties, i.e.

· H





(11)



(12)



(21)



(22)





· I

= µ · I

(7)

where I

is the identity matrix of dimension 2, and

(·)

denotes the conjugate transpose matrix opera-

tion. For the case of perfect channel knowledge at

the receiver, the output of the combiner representing

the decision statistics (soft decisions) are given as fol-

lows:

S =

· R

· (H

· S + N) ⇔

S = S + N

(8)

which indicates that except the noise term the symbols

have been recovered at the combiner’s output. In a

real system the MIMO channel has been estimated at

the receiver non perfectly giving the following soft

decision metric:

S =

· R

· (H

· S + N) ⇔

S = H

res

· S + N

(9)

where the subscript res indicates the residual chan-

nel effect that have to be compensated by the ML de-

coder. In case of signiﬁcant temporal channel varia-

tion during the transmission of an orthogonal scheme,

the orthogonality is lost causing intersymbol interfer-

ence. Hence, in order to preserve the orthogonality,

the sampling theorem has to be applied determining

the relative distances in time and frequency dimen-

sion that the pilots have to be placed. In space-time

block codes the distance is proportional to the coher-

ence time, while in space-frequency block coding is

proportional to the coherence bandwidth. The chan-

nel tracking is performed through the phase estima-

tion at the pilot positions based on the ML criterion

according to the equation:

= arg min

∠

i=1

(pre)∗

(10)

where

and

(pre)

are the current channel esti-

mates at pilot positions and the estimates at the same

subcarrier i during the preamble OFDM symbol re-

spectively. The estimated phase difference updates

the preamble based estimation. The ﬁnal channel es-

timates at the pilot positions are interpolated (linearly

in our case) in order to obtain the estimates in all sub-

carriers. A sample of the channel compensated sym-

bols, just before the detector, is given in ﬁg.4, where

the blue dots are the transmitted ones before the SFBC

encoder. The speciﬁc snapshot corresponds to a 2 × 2

MIMO-OFDM system with 16QAM and total cod-

ing (RS-CC) 3/4 in a channel type A (802.16e, 3GPP

standard) operating in E

= 15dB. In addition,

QPSK modulation is observed due to the FCH sym-

bols. Quantitatively, the maximum achievable diver-

sity order is a product of the number of transmit anten-

nas, the number of receive antennas, and the number

of resolvable paths (Bolcskei and Paulraj, 2001).

Figure 4: Constellation map of the channel compensated

symbols (red) with respect to the transmitted ones (blue).

4 EVALUATION RESULTS

To study the impact of realistic channel estimation ar-

chitecture on MIMO-OFDM performance, a 2×1 and

2 × 2 MIMO-OFDM system with orthogonal space

frequency design has been designed, modelled and

simulated, taking into account all stages in RF, IF and

baseband level, as well as their relative requirements.

The simulated system achieves information data rates

of 6.9Mbps at BPSK-1/2, of 13.8Mbps at QPSK-1/2,

of 20.7Mbps at QPSK-3/4, of 27.7Mbps at 16QAM-

1/2, of 41.5Mbps at 16QAM-3/4, of 55.3Mbps at

64QAM-2/3, and of 62.2Mbps at 64QAM-3/4 in a

frequency bandwidth of 20MHz at a center frequency

of 5.2GHz. The relative frequency spectrum at a

transmit antenna and a receive antenna is given in

ﬁg.5 for the 16QAM-3/4 case in a propagation chan-

nel of type A (802.16e) and for E

= 10dB. The

frequency selectivity is obvious, as well as the noise

distortion is becoming quite severe.

The channel adaptation is based on 8 pilot symbols

per OFDM symbol placed in blocks of 2 adjacent

subcarriers. OFDM stages are based on a 256-point

FFT/IFFT with cyclic preﬁx of 1/4. Each frame car-

ries 2400 information bits and the evaluation is per-

formed on the basis of achieving BER estimation rel-

ative variance of 0.0001 with an upper limit of 1000

frames. The performance of the channel estimator

Figure 5: Frequency spectrum at the Tx antenna (red) and

the corresponding Rx one (blue) for 2 × 2 OFDM system.

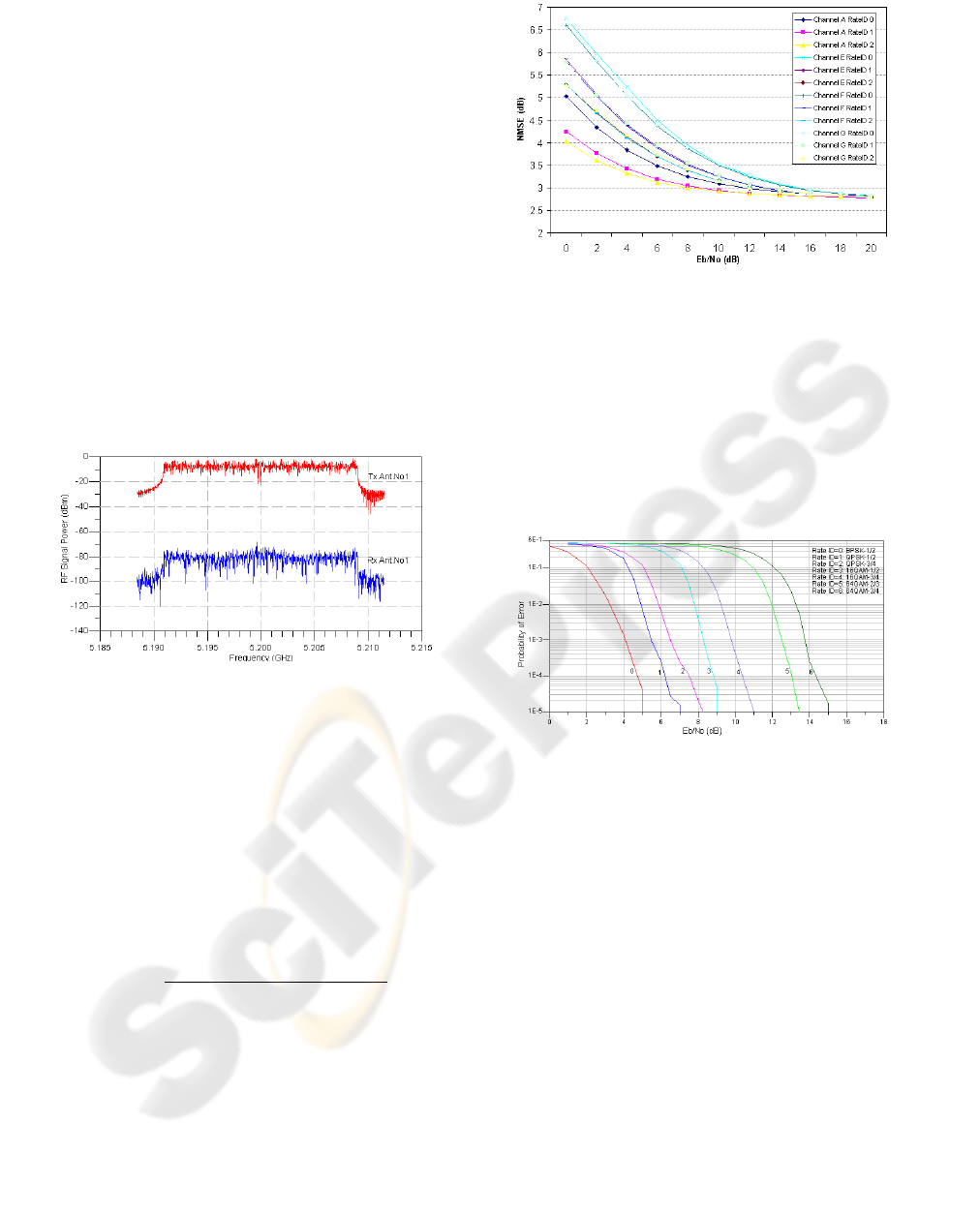
with respect to the actual channel propagation con-

ditions is based on normalized mean square error

(NMSE), according to the formula (11) and the re-

sults are given in ﬁg.6 for the 2 × 2 MIMO-OFDM

case and for various propagation channels and data

rates. Based on these results the channel estimator

is characterized by an irreducible error ﬂoor at 3dB,

achieving the limit at E

= 13dB for all schemes

and channel conditions tested.

NMSE =



)

−

)



)



(11)

The total system performance of 2 × 1 and 2 × 2

MIMO-OFDM system has been evaluated based on

the information bit error rate giving an insight at the

sensitivity of the channel estimation errors in the efﬁ-

ciency of the system. For the probability of error P

measurement to be statistically signiﬁcant, the rela-

tive variance R

v ar

of P

is taken into account for N

transmitted bits indicating the conﬁdence interval of

. In ﬁg.7 the probability of error has been produced

Figure 6: Normalized MSE of the overall channel estima-

tion in various propagation channels and data rates for 2 × 2

MIMO-OFDM case.

for 2× 1 case, in channel type A of 802.16e for all the

modulation formats and coding modes. It is worth

noticing that for the information data rate of 6.9Mbps

a value of E

= 4.5dB is enough to achieve

P e = 10

−4

, while the same value for 62.2Mbps re-

quires almost 10dB increase in E

. In ﬁg.8 the

Figure 7: Probability of error for a 2 × 1 OFDM system in

propagation channel type A.

performance of a 2 × 1 OFDM system has been eval-

uated for various channel types of 802.16e standards.

The system performs better for channel type A, but

for more demanding channels (E,F,G), with higher

mobility or frequency selectivity, the system fails to

support increased data rates in relatively small val-

ues E

. In ﬁg.9 the performance of 2 × 2 MIMO

OFDM system has been depicted for various propa-

gation channels and data rates indicating that the pro-

posed scheme is quite efﬁcient in propagation chan-

nels that follow the channel models of type A, E, or

G. Furthermore, the proposed scheme is characterized

by bit error rate achievable ﬂoors as E

increases

in channel models with increased frequency selectiv-

ity.

Finally, for comparison reasons, the system has

been also implemented with space-time block coding

(STBC) and for the 2 × 1 OFDM case the results are

given in ﬁg.10. The performance gain for the SFBC

Figure 8: Perfromance of a 2 × 1 OFDM system in various

propagation channels and data rates.

Figure 9: Performance evaluation of a 2 ×2 OFDM system.

scheme at a probability of error P

= 10

−3

is about

2dB for a data rate of 20.7Mbps in a channel of type

A, whilst for 13.8Mbps the gain is about 1.5dB in

channels of types G and F.

5 CONCLUSIONS

In this paper a MIMO multicarrier system has been

designed and evaluated giving rise to space-frequency

orthogonality. In addition, all the RF stages at the

transmitter and the receiver were taken into account

approaching a real architecture as close as possible.

An efﬁcient channel estimation scheme was incorpo-

rated in the system achieving not only a good efﬁ-

ciency, but also low computational requirements since

the processing is performed in one OFDM symbol

and the channel estimation during the frame is limited

only in the varying propagation characteristics. The

overall system performance of SFBC MISO/MIMO

OFDM was evaluated for various propagation chan-

nels resulting in very good performances for propa-

gation conditions that are characterized by low fre-

quency selectivity, since the pilot overhead is only

3.12%.

Figure 10: Comparison between SFBC (solid) and STBC

(dash) schemes for 2 × 1 case.

REFERENCES

A. Adjoudani et al. “Prototype Experience for MIMO

BLAST Over Third-Generation Wireless System”,

IEEE Journal on Selected Areas in Communications,

Vol. 21, No. 3, pp. 440 - 451, April 2003.

V. Tarokh, N. Seshadri, A. Calderbank, “Space-Time Codes

for High Data Rate Wireless Communication: Perfor-

mance Criterion and Code Construction”, IEEE Trans

of Information Theory, vol.44, pp744-765, March

1998.

H. Bolcskei, A. Paulraj, “Space-Frequency Codes for

Broadband Fading Channels”, IEEE International

Symposium on Information Theory, pp. 219, June

2001.

V. Tarokh, H. Jafarkhani, A. Calderbank, “Space-Time

Block Codes for orthogonal designs”, IEEE Trans of

Information Theory, vol.45, pp1456-1467, June 1999.

Y. Li, N. Seshadri, S.Ariyavisitakul, “Channel Estima-

tion for OFDM Systems with Transmitter Diversity

in Mobile Wireless Channels”, IEEE Journal of Se-

lected Areas in Communications, vol.17,No3,p.461-

471, March 1999.

3GPP TR 25.996 v6.1.0, (2003-2009), “Spatial Channel

Model for Multiple-Input Multiple Output Simula-

tions”,

IEEE Std 802.16.2-2004, “Recommended Practice for Lo-

cal and metropolitan area networks”, 17 March 2004.

S. Alamouti, “A Simple Transmit Diversity Technique for

Wireless Communications”, Journal of Selected Areas

in Communications, vol.16, No8, October 1998.

G. Stuber J. Barry, S. Mclaughlin, Y. Li, M. Ingram, T.

Pratt, “Broadband MIMO-OFDM Wireless Commu-

nications”, Proceedings of the IEEE, vol.92, No2,

February 2004.

Agilent, “MIMO Wireless LAN PHY Layer [RF] Opera-

tion & Measurement, Application Note 1509”, 1509,

16/9/2005.