USING ATTACK GRAPHS IN AD HOC NETWORKS

For Intrusion Prediction Correlation and Detection

Marianne Azer

National Telecommunication Institute, Cairo, Egypt

Sherif El-Kassas

Department of computer science, American University in Cairo, Cairo, Egypt

Magdy El-Soudani

Department of Electronics and Communications,Faculty of Engineerin, Cairo University, Cairo, Egypt

Keywords: Anomaly detection, attack graphs, intrusion detection, security in ad hoc networks.

Abstract: Ad hoc networks have lots of applications; however, a vital problem concerning their security aspects must be

solved in order to realize these applications. Hence, there is a strong need for intrusion detection as a frontline

security research area for ad hoc networks security. Among intrusion detection techniques, anomaly detection

is advantageous since it does not need to store and regularly update profiles of known attacks. In addition the

intrusion detection is not limited to the stored attack profiles, which allows the detection of new attacks.

Therefore, anomaly detection is more suitable for the dynamic and limited resources nature of ad hoc

networks. For appropriately constructed network models, attack graphs have shown their utility in organizing

combinations of network attacks. In this paper, we suggest the use of attack graphs in ad hoc networks. As an

example, we give an attack graph that we have created for the wormhole attack. For anomaly prediction,

correlation, and detection in ad hoc networks, we suggest the use of two methods that rely basically on attack

graphs. The first method is based on the attack graph adjacency matrix and helps in the prediction of a single

or multiple step attack and in the categorization of intrusion alarms’ relevance. The second method uses the

attack graph distances for correlating intrusion events and building attack scenarios. Our approach is more

appropriate to ad hoc networks’ collaborative and dynamic nature, especially at the application level.

1 INTRODUCTION

Mobile ad hoc networks security has recently been

the topic of extensive research. Intrusion detection is

considered as a frontline security research area under

the umbrella of ad hoc networks security. Intrusion

detection techniques can be classified into misuse

detection and anomaly detection. In this paper we

focus on the anomaly detection. Among the anomaly

detection techniques are the ones suggested in

(Zhang,

Lee, and Huang, 2003

) and (Yi et al., 2005).

Attack graphs have shown their utility in organizing

combinations of network attacks. We suggest the use

of attack graphs in ad hoc networks and give as an

example an attack graph that we created for the

wormhole attack. For intrusion correlation,

prediction and detection in ad hoc networks, we

present two methods that rely basically on attack

graphs. The first is based on the attack graph

adjacency matrix and helps in the prediction of a

single or multiple step attack and in the

categorization of intrusion alarms' relevance. The

second method uses the attack graph distances for

correlating intrusion events and building attack

scenarios.

The remainder of this paper is organized as

follows. In section 2, we give a brief introduction to

the concept of attack graphs and adjacency matrices;

the attack graph of the wormhole attack is given as an

example. Section 3 discusses the possible use of

attack graph adjacency matrices and attack graph

distances for intrusions prediction and correlation.

Finally, in section 4 we conclude this paper and

discuss some future work.

Azer M., El-Kassas S. and El-Soudani M. (2006).

USING ATTACK GRAPHS IN AD HOC NETWORKS - For Intrusion Prediction Correlation and Detection.

In Proceedings of the International Conference on Security and Cryptography, pages 63-68

DOI: 10.5220/0002097700630068

 SciTePress

2 ATTACK MODELS

In this section we give some background about the

attack graphs, adjacency matrices, and risk

management. Section 2.1 introduces the concept of

attack graphs and adjacency matrices; section 2.2

explains the risk management for ad hoc networks

using the vulnerability attack graph.

2.1 Attack Graphs and Adjacency

Matrices

Network attack graphs represent a collection of

possible penetration scenarios in a computer network.

The graph can focus on the extent to which an

adversary can penetrate a network to achieve a

particular goal, given an initial set of capabilities.

They represent not only specific attacks but

categories of attacks. They can detect previously

unseen attacks which have common features with

attacks in graphs.

Graphs can also be represented in the form of

adjacency matrices or adjacency lists. We will focus

on adjacency matrices. The relationship between a

graph and its adjacency matrix is studied in spectral

graph theory.

If A is the adjacency matrix of the directed or

undirected graph G, then the matrix A

, i.e. the matrix

product of n copies of A, has an interesting

interpretation: the entry in row i and column j gives

the number of directed or undirected paths of length n

from vertex i to vertex j. In general, to generate the

matrix of path of length n, take the matrix of path of

length n-1, and multiply it with the matrix of path of

length 1 (Cormen et al., 2001).

2.2 Risk Management

A five step procedure was given in (Dantu,, Loper

and Kolan, 2004) to calculate vulnerabilities and

risks of a critical network resource. The same

procedure could be customized and applied for ad

hoc networks. The risk management method for ad

hoc networks, using attack graphs is illustrated in

Figure 1 and has the following steps:

Step 1->Creation of an attacker Profile: The

profile gives the expendable resources associated

with the attacker. Creating an attack profile would

help in identifying the probable attacks and the

probable network resources that can be compromised

by the attacker. An attacker may be classified

depending on: his effects to active and passive, his

source to external and internal, depending on his

capabilities to mote and laptop-class and finally

based on the target operation of the attack to routing

and packet forwarding attacker.

Step 2->Creation of Attack Graph: Attack graphs

depict ways in which an adversary exploits system

vulnerabilities to achieve a desired state. System

administrators use attack graphs to determine how

vulnerable their systems are and to determine what

security measures need to be deployed in order to

defend their systems. Using this graph, we can learn

how intruders culminate sequence of state transitions

for achieving an attack. To build an attack graph, the

ad hoc network should be modeled as a finite state

machine, where state transitions correspond to atomic

attacks launched by the intruder. Also a desired

security property could be specified and the

intruder’s goal generally corresponds to violating this

property more details for building and analyzing

attack graphs could be found in (Sheyner, and Wing,

2003), (Sheyner et al., 2003), and (Swiler, Phillips

and Gaylor, 1998). Attack graphs construction

depends on the knowledge of different types of

attacks to which the network is vulnerable. In ad hoc

networks, there are two main types of passive attacks;

the eavesdropping and the traffic analysis attack.

Active attacks can be subdivided into the following

categories: impersonation, masquerade, replay,

modification of messages, and denial of service.

Step 3-> Labeling Attack Paths with Behavior

Attributes: Based on the type of the attacker, the

attack paths are considerably different depending on

the type of quantifying variable in consideration. This

helps us in deducing all the vulnerable resources in a

network for a given attack profile.

Step 4->Risk Computation: In this step, a risk

level for all the critical resources is calculated based

on the set of paths, attributes and attacker type.

Bayesian networks-based estimation is used for

calculating the aggregated risk value of the resource.

Next, a resource is marked as attack prone if this

value is more than a threshold. Bayesian networks

encode the probability relationships between various

random variables or nodes in a causal graph and

therefore we can model the attack trees by reducing

them to causal graphs and associating the nodes or

random variables with probabilities. Therefore, we

document all the attack paths for a given resource and

calculate the Bayesian probabilities of the root nodes

of each attack path when the evidence regarding the

leaf is available.

Step 5->Optimizing the risk level: In a typical

network, patching vulnerability may impact other

network elements. Steps 1-4 need to be performed

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

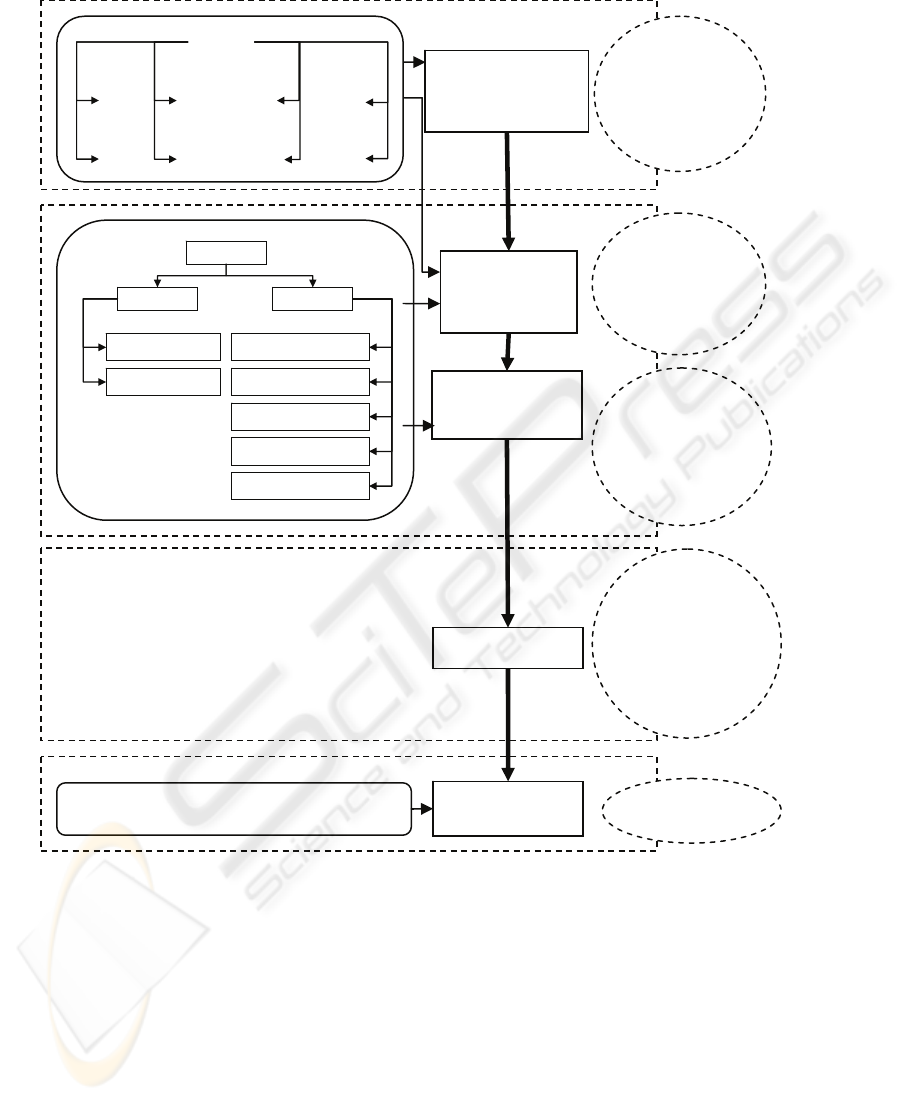
Figure 1: Risk management for ad hoc networks using behavior based attack graphs.

repeatedly for an optimum risk value.

3 ATTACK MODELS

There are lots of anomaly detection approaches for ad

hoc networks, such as using classifiers, finite state

machines and game approach. Those techniques are

more suitable for well understood protocols such as

routing protocols. However, since self contained

protocols are very limited in ad hoc networks, these

approaches might not be appropriate in some cases.

For example, it is very difficult to model attacks on

ad hoc networks collaborative applications as one

state machine or to use a classifier or the game

approach. In addition, the use of attack graphs in

intrusion detection will not add an additional burden

since it must be constructed, anyway, for risk

assessment.

A particularly severe security attack, called the

wormhole attack has recently been introduced in the

context of ad hoc networks (Karlof and Wagner,

2003), (Hu, Perrig, and Johnson, 2003), (Hu, and

Evans, 2004). During the attack (Khalil, Bagchi, and

Shroff, 2005), a malicious node captures packets

from one location in the network, and “tunnels” them

Create attack

graph

Input

Risk management step

Attackers

Active

Passive

External

Internal

Mote

Laptop

Packet

Routing

Create an attacker

profile and see attacker

resources

Attacks

Active Passive

Eavesdropping

Traffic Analysis

Impersonation

Masquerade

Replay

Modification

Denial of service

Label attack paths

with behavior

attributes

Risk Computation

Patching vulnerabilities and repeating previous steps

Optimizing risk level

Identify probable

attacks and

network

resources that

can be

com

romised

Learn sequence

of state

transitions for

achieving an

attac

Deduce all

vulnerable

resources in the

network for a

given attack

rofile

Risk level for

critical resources is

computed.

If risk level

>threshold,

resource is attack

prone

Optimum risk

value

Benefit form risk

management

USING ATTACK GRAPHS IN AD HOC NETWORKS - For Intrusion Prediction Correlation and Detection

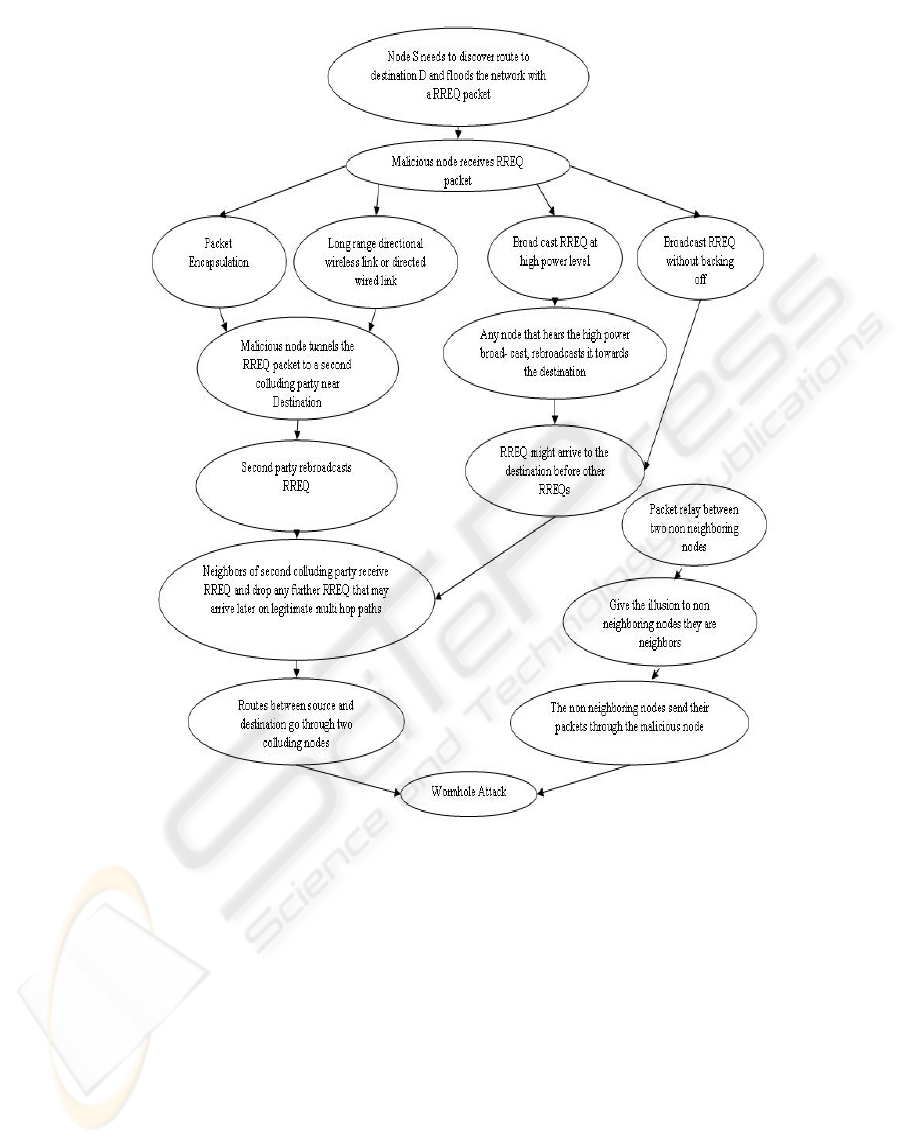
Figure 2: The Wormhole attack graph.

to another malicious node at a distant point, which

replays them locally. Figure 2 depicts the attack

graph that we have created for the wormhole attack

using the attack modes described in (Khalil, Bagchi,

and Shroff, 2005).

In section 3.1 the use of the attack graph adjacency

matrix for intrusion prediction and intrusion alarms

categorization is suggested, whereas section 3.2 is

concerned with the correlation of intrusion events and

building attack scenarios through attack graph

distances.

3.1 Use of the Adjacency Matrix

For n vertices in the attack graph, the adjacency

matrix A is an n ×n matrix where element a

of A

indicates the presence of an edge from vertex i to

vertex j. A particular matrix clustering algorithm

(Chakrabarti et al., 2004) is designed to form

homogeneous rectangular blocks of matrix elements

such that the clusters form regions of high and low

densities. As it was suggested in (Noel and Jajodia,

2005), the adjacency matrix, if taken directly, shows

every possible single-step attack. Also if A

calculated, using the transitive closure of A, it tells

whether there is at least one p- step attack from one

vertex to another. A multi-step reachability matrix

can be computed form the adjacency matrix and it

helps to identify the minimum number of steps

required to reach each pair of attack vertices. A

method for attack prediction and alarm categorization

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

using the adjacency matrix A, the computed transitive

closure, and the multi-step reachability matrix after

having applied the clustering algorithm is explained

in (Noel and Jajodia, 2005). When an intrusion alarm

is generated, it can be associated with the adjacency

matrix for single step reachability, with the multi-step

reachability matrix for multi-step reachability, or

with the transitive closure of A for all step

reachability. From this, the intrusion alerts can be

categorized based on the number of associated attack

steps. If an attack occurs within a zero-valued region

of the transitive closure, it might be concluded as a

false alarm, or if an alarm occurs within a single step

region of the reachability matrix, it is indeed one of

the single-step attacks in the attack graph.

Somewhere in between, if an alarm occurs in a p-step

region, the attack graph predicts it takes a minimum

of p-steps to achieve such an attack. By associating

intrusion alarms with a reachability graph, the origin

and impact of the attack can also be predicted. This

general approach, in (Noel and Jajodia, 2005) for

different network security situations can be applied to

our wormhole attack graph and generalized to ad hoc

networks after creating network attack graphs for the

different attacks, knowing the special vulnerabilities

of this type of networks.

3.2 Use of Attack Graph’s Distances

In (Noel, Robertson, and Jajodia, 2004) an idea for

correlating intrusion events and building attack

scenarios through attack graph distances was

suggested. This idea could be applied as well in our

case for the wormhole attack detection and in general

for any ad hoc network’s attack graph. To determine

the degree of correlation, the graph distance between

corresponding exploits is measured. Two events that

fall on a connected path in an attack graph are

considered correlated, at least to some extent. The

graph distance between a pair of exploits is the

minimum length of paths connecting them, as the

shortest path is the best assumption for event

correlation and the most efficient to compute. The

graph distances are unweighted, i.e. no weights are

applied to graph edges between exploits. Once the

exploit distances are computed for an attack graph,

they are applied continuously for real time stream of

intrusion events. The inverse of the events distance is

computed and applied to an exponentially weighted

moving average filter, used to provide resiliency

against detection errors, to obtain the filtered version

of the original sequence of event distances. These

filtered inverse events distances constitute the basic

measure of event correlation in that model; a proper

threshold is applied to the filtered distances to

separate event paths into highly correlated attack

scenarios. An overall relevancy score is also

computed for each attack scenario as a function of the

number of events in the scenario. This relevance

score is the proportion of the attack paths actually

occupied by an attacker scenario’s intrusion events.

This same idea could be applied for ad hoc networks

intrusion correlation after having assessed all the

vulnerabilities and created the network attack graph.

In our approach, we will assume that there are

central distributed authorities responsible of building

the attack graphs, calculating their corresponding

adjacency matrix, and computing the attack graph

distances. They should also be responsible of

distributing this data to the nodes and informing the

nodes of the current status whenever there is an attack

so that nodes could locate the most recent event on

their attack graphs. This is not our ultimate goal, but

we shall start our work based on this assumption and

then enhance our approach. Figure 3 summarizes the

suggested anomaly detection technique for ad hoc

networks using attack graphs.

4 CONCLUSIONS AND FUTURE

WORK

In this paper we focused on the anomaly detection

approach for intrusion detection in ad hoc networks.

Some anomaly detection methods such as classifiers,

state machines, and game approach are suitable for

well understood protocols such as routing protocols.

However, since self contained protocols are limited

in ad hoc networks, these approaches might not be

appropriate in some cases. Also, since the risk

assessment methodology described in this paper uses

attack graphs anyway, we suggested the use of attack

graphs for ad hoc networks. As an example for attack

graphs, we created an attack graph for the wormhole

attack. Based on this attack graph we discussed two

methods for anomaly detection that rely basically on

the constructed attack graph for intrusion detection.

The first was based on the attack graph adjacency

matrix and helped in the prediction of a single or

multiple step attack and in the categorization of

intrusion alarms’ relevance. The second method used

the attack graph distances for correlating intrusion

events and building attack scenarios. Therefore, our

approach is more appropriate to ad hoc networks’

collaborative and dynamic nature, especially at the

application level. In the future we intend to build a

full ad hoc network environment and use the

suggested anomaly detection approach to evaluate it

USING ATTACK GRAPHS IN AD HOC NETWORKS - For Intrusion Prediction Correlation and Detection

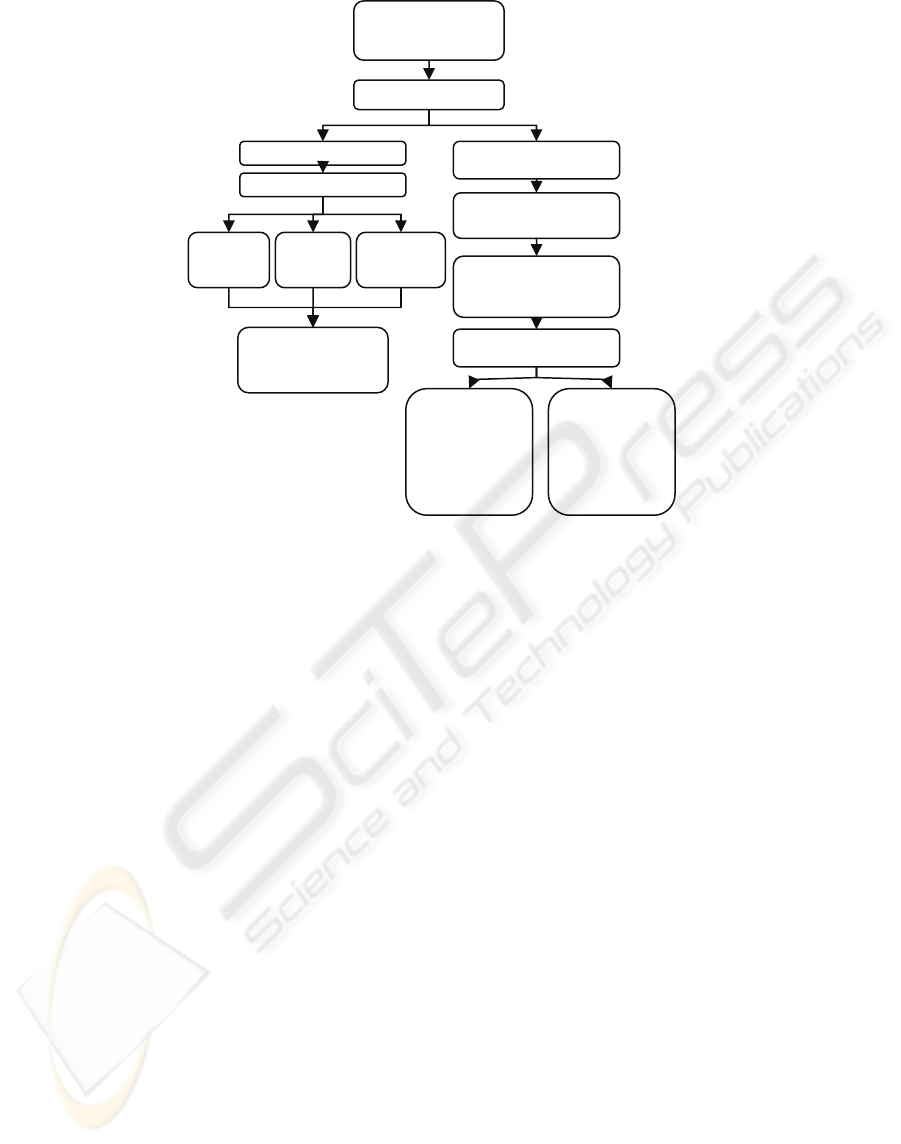
Figure 3: Suggested anomaly detection.

and compare it with other anomaly detection

techniques.

REFERENCES

Zhang, Y., Lee, W., and Huang, Y. 2003. Intrusion

Detection Techniques for Mobile Wireless Networks,

ACM WINET.

Yi, P., et al.2005. Distributed Intrusion Detection for

Mobile Ad hoc Networks, Proceedings of the 2005

Symposium on Applications and the Internet

Workshops (SAINT-W’05), 94-97.

Cormen, T., et al. 2001. Introduction to Algorithms,

Second Edition. MIT Press and McGraw-Hill, Section

22.1: Representations of graphs, 527–531.

Dantu, R., Loper, K., Kolan, P., 2004. Risk Management

using Behavior based Attack Graphs, International

Conference on Information Technology: Coding and

Computing (ITCC'04) Volume 1.

Sheyner, O., and Wing, J.,2003. Tools for Generating and

Analyzing Attack Graphs, FMCO 2003, 344-372.

Sheyner, O., Haines, J., Jha, S., Lippmann, R., and Wing, J.,

2002, Automated Generation and Analysis of Attack

Graphs, IEEE Symposium on Security and Privacy

2002, 273-284.

Swiler, L., Phillips, C., and Gaylor, T., 1998. A

Graph-Based Network-Vulnerability Analysis System,

tech. report, Sandia National Labs.

. Karlof, C., and Wagner, D., 2003. Secure Routing in

Sensor Networks: Attacks and Countermeasures, at the

1st IEEE International Workshop on Sensor Network

Protocols and Applications.

Hu, Y., Perrig, A., and Johnson, D., 2003. Packet leashes: a

defense against wormhole attacks in wireless networks,

in Proceedings of the 22nd Annual Joint Conference of

the IEEE Computer and Communications Societies

(INFOCOM), 1976-1986.

Hu, L., and Evans, D., 2004. Using Directional Antennas to

Prevent Wormhole attacks, in Network and Distributed

Systems Security Symposium.

Khalil, I., Bagchi, S., and Shroff, N., 2005. LITEWORP: A

Lightweight Countermeasure for the Wormhole Attack

in Multihop Wireless Networks, DSN 2005, 612-621.

Chakrabarti, et al., 2004. Fully Automatic

Cross-Associations, in Proceedings of the 10th ACM

International Conference on Knowledge Discovery &

Data Mining, Seattle, Washington, August 2004.

Noel, S., Jajodia, S., 2005. Understanding Complex

Network Attack Graphs through Clustered Adjacency

Matrices, acsac, 21st Annual Computer Security

Applications Conference (ACSAC'05), 160-169.

Noel, S., Robertson, E., and Jajodia, S., 2004. Correlating

Intrusion Events and Building Attack Scenarios

through Attack Graph Distances," acsac, 20th Annual

Computer Security Applications Conference

(ACSAC'04), 350-359.

Assess ad hoc network

vulnerabilities and

possible attacks

Construct attack graph

Com

ute ad

acenc

matrix

matrix clusterin

Single step

reachability

matrix

Transitive

Closure

p-step

reachability

matrix

Intrusion alarm

categorization and

intrusion prediction

Calculate unweighted graph

distances

Calculate the inverse of

events distances

Apply the sequence to an

exponentially weighted

moving average filter

Obtain filtered inverse

eve

ces

Apply filtered

distances to a

threshold to

separate event

paths to highly

correlated attack

scenarios

Calculate

relevancy score for

each attack

scenario

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY