FLEXIBLE COMPLETION OF WORKFLOW ACTIVITIES

Georg Peters

Munich University of Applied Sciences, Department of Computer Science

Lothstrasse 34, 80335 Munich, Germany

Roger Tagg

University of South Australia, School of Computer and Information Science

Mawson Lakes, SA 5095 Australia

Keywords: Workflow management, Flexible workflow, Partial completion, Limitations of workflow systems.

Abstract: Over the last twenty years business process management has become a central approach to maintaining the

competitiveness of companies. However the automation of the business processes utilizing workflow

systems have often led to over-structured solutions that lack of the flexibility inherent in the underlying

business model. Therefore there is a need to develop flexible workflow management systems that easily and

quickly adapt to dynamically changing business models and processes. Lin and Orlowska (2005) introduced

partly complete-able activities as one way to make workflow systems more flexible. In our paper, we extend

the concept of partly complete-able activities by recognizing separate probability and fuzzy dimensions and

by introducing process memory.

1 INTRODUCTION

Since its appearance twenty years ago, business

process modelling has become one of the core

methods to organizationally develop companies with

the objective of improving their performance (van

der Aalst and van Hee 2002). In the implementation

and support of processes using information

technology, workflow systems are of special

importance.

However, after a period of high expectations in

workflow system technology in the middle of

nineties, a period of disappointment followed around

the millennium. Currently it is experiencing a

revival, as a core element of the new generation of

ERP systems based on middleware technology.

One of the areas of disillusionment around the

millennium was where workflow systems replaced

human-oriented processes that are characterized by

high flexibility: a simple transfer of the rigid

concepts of manufacturing to service processes

delivers suboptimal outcomes or results in failure.

Interactive or semi-automated workflows need to

adapt to their human participants, and therefore need

to support high degrees of flexibility.

However, examples of workflow systems that

cater well for flexibility still mostly occur in

research laboratories rather than in commercial

products. Examples are Adept (Reichert 1998) or

Chameleon (DSTC Praxis Project 2004, Sadiq

2000). A range of dimensions of flexibility was also

discussed by Tagg (2003).

One example for flexibility is the ease with

which an individual workflow instance (or business

case) can be allowed to diverge from the general

pattern. This is typically required because processes

fall behind schedule and need to be got back on

track by such means as increasing resources or

taking agreed short cuts. One specific type of short

cut is to allow progression of the workflow before

some activities have been fully completed. But in

virtually all commercial workflow systems, an

activity is only considered as completed when all its

post-conditions have been fulfilled. Lin and

Orlowska (2005) suggested the concept of partly

complete-able activities to relax this constraint

(please note, we use activity in the sense of Carter et

al. (2004): we do not differentiate between task and

activity).

The objective of our paper is to extend the

concept of partly complete-able activities by

173

Peters G. and Tagg R. (2006).

FLEXIBLE COMPLETION OF WORKFLOW ACTIVITIES.

In Proceedings of the Eighth International Conference on Enterpr ise Information Systems - ISAS, pages 173-180

DOI: 10.5220/0002444901730180

 SciTePress

distinguishing fuzzy and probability dimensions.

Besides that we introduce a memory component to

such processes, in order to further increase

flexibility. Last but not least we briefly analyze the

potential of partly complete-able activities for

current workflow systems.

The paper is organized as follows. In section 2

we describe the concept of partial completion of

activities (Lin, Orlowska 2005). In the following

section we introduce the probability and fuzzy

dimensions to partly complete-able activities;

furthermore we investigate some implications of

memory to a process with partly complete-able

activities. The paper concludes with a summary.

2 PARTIAL COMPLETION OF

ACTIVITIES

2.1 Partly Complete-able Activities

Without loss of generality let us assume a sequential

workflow. A central prerequisite to start activity A

is that its predecessor, the activity A

n-1

, has been

completed. As long as the post-conditions of A

n-1

are

not fully completed the workflow system cannot

continue to the next activity. This behaviour can be

characterized as all-or-nothing strategy. It leads to a

somewhat inflexible behaviour of the workflow

system (Lin, Orlowska 2005).

To achieve more flexibility in the completion of

activities Lin and Orlowska introduced the concept

of partly complete-able activities. The possible

states of a classic activity not-completed or

completed are augmented by a third state, partly

completed. Allowing partial completion of activities

can lead to a higher flexibility of the process and a

better alignment to real life situations. According to

Lin and Orlowska, the main advantages obtained by

this concept are a reduced processing time and an

earlier release of resources for other activities.

Partly complete-able activities are characterized

by the following property. The objective of an

activity is decomposable: the activity can be

completed on different levels denoted as L

,…,

,…,L

, where L

defines the minimum

requirements and L

indicates full completion.

This property implies that the absolute

completion of the activity is not critical for the

process. As long as all activities are partly

completed at least on the level L

, the process

outcome still meets at least its minimum objectives.

The decision whether an activity is completed or

not goes as follows. For levels of completion lower

than L

and for full completion (L

) the decision

process is the same as in classic workflow systems.

If the level of completion is lower than L

the

workflow systems treats the activity as not

completed and therefore does not proceed to the

consecutive activity. If the full completion level L

is reached the workflow system automatically

continues with the next activity.

However, if the activity is completed at least to

the level L

but less than L

the workflow system

presents the activity to an external decision maker,

in most cases probably the process owner, who

decides whether or not the activity can be considered

as completed. If yes, the workflow system closes the

activity and continues with the next process step.

open

not_active

commence

closed

active

aborted

scheduled

suspended

commenced

suspend

resume

completed

partly_ completed:

N-1

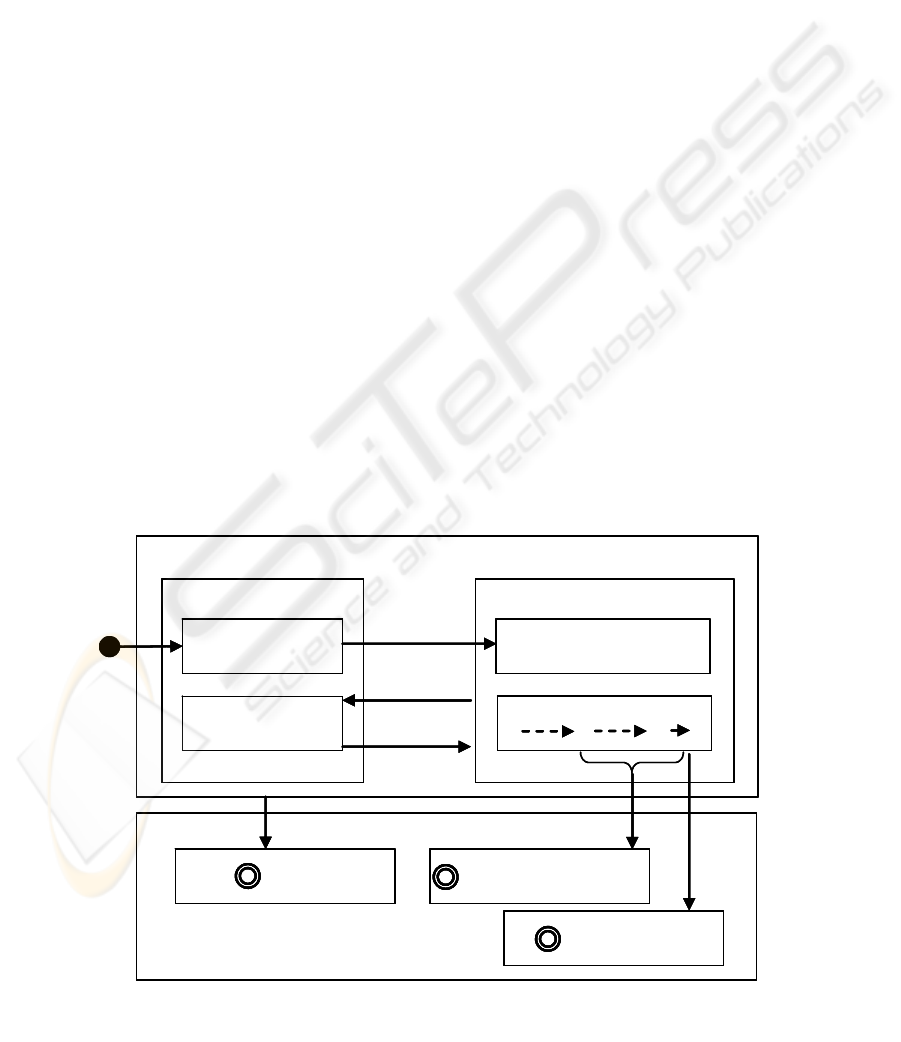
Figure 1: Enhanced Activity Finite State Machine

(according to Lin and Orlowska [2005])

open

not_active

commence

closed

active

aborted

scheduledscheduled

suspendedsuspended

commenced

suspend

resume

completedcompletedcompleted

partly_ completed:

N-1

Figure 1: Enhanced Activity Finite State Machine

(according to Lin and Orlowska [2005])

Figure 1: Enhanced Activity State Machine (according to (Lin and Orlowska, 2005)).

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

174

2.2 Finite State Machine

To formally model the concept of partial

completion, Lin and Orlowska developed an

enhanced activity finite state machine (Fig. 1) as a

generalization of the state model of the WFMC

(1995):

An activity can have the states open and closed.

In the open state it is scheduled and therefore not

active: open.not_active.scheduled. When the

performer picks the activity out of a work-item list it

changes its state to open.active.commenced. If a sub-

objective of the activity is completed the state

changes to open.active.partly_completed.

As already defined above the level of completion

is indicated by L

, L

, …, L

with L

the

level of full achievement of the objective of the

activity and L

the minimum requirements. If the

activity reaches the levels L

, … L

N-1

the process

owner can decide that the activity is sufficiently

completed. In that case the activity changes to its

final state closed.completed. This state will also be

reached when the level L

is achieved since the

workflow engine automatically closes the activity.

Anytime during the activity is open.active.com-

menced it can be set on “Wait”: not_active.

suspended and resumed accordingly. The activity

also can be aborted (closed.aborted ) at any time.

3 AN ENHANCED MODEL OF

PARTIAL COMPLETION

3.1 Probabilistic and Fuzzy

Enhanced Finite State Models

3.1.1 Fuzzy and Probability Concepts

Lin and Orlowska introduced a model of partly

complete-able activities without specifying the

phenomena that can lead to the different levels of

completion. We will distinguish between the fuzzy

sets and probability as two possible reasons for the

partial completion.

The relationship of fuzzy sets (Zimmermann

2001) and probability has been intensively and

controversially discussed (e.g. Klir 1989, Zadeh

1983, 1995) since Zadeh introduced fuzzy sets in

1965. Recently, it has become accepted that they can

be considered as independent and complementary to

each other. Fuzzy sets are indicators for similarities

or neighbourhood relations while probability is

related to probabilistic uncertainty.

Note, that fuzziness is often also regarded as one

form of uncertainty (Klir 1989, Zimmermann 2001).

However this uncertainty is related to e.g. linguistic

variables. What does the term “rich” mean:

$1million, $10million or $100million? Therefore

linguistic variables are described as membership

functions. To avoid confusing this with fuzzy

uncertainty we explicitly refer to probabilistic

uncertainty when we are in the field of probability

theory.

Fuzzy Concept

For example, a bank wants to classify its customers

into two groups: rich and poor customers. Obviously

there is no crisp separation between rich and poor -

e.g. in a way that customers that own less than $ 1

million are poor while people with a fortune of $ 1

million and more are rich. It is more intuitive that a

person with a wealth of – let’s say – $ 1.1 million is

considered as reasonably rich but still a little bit

poor.

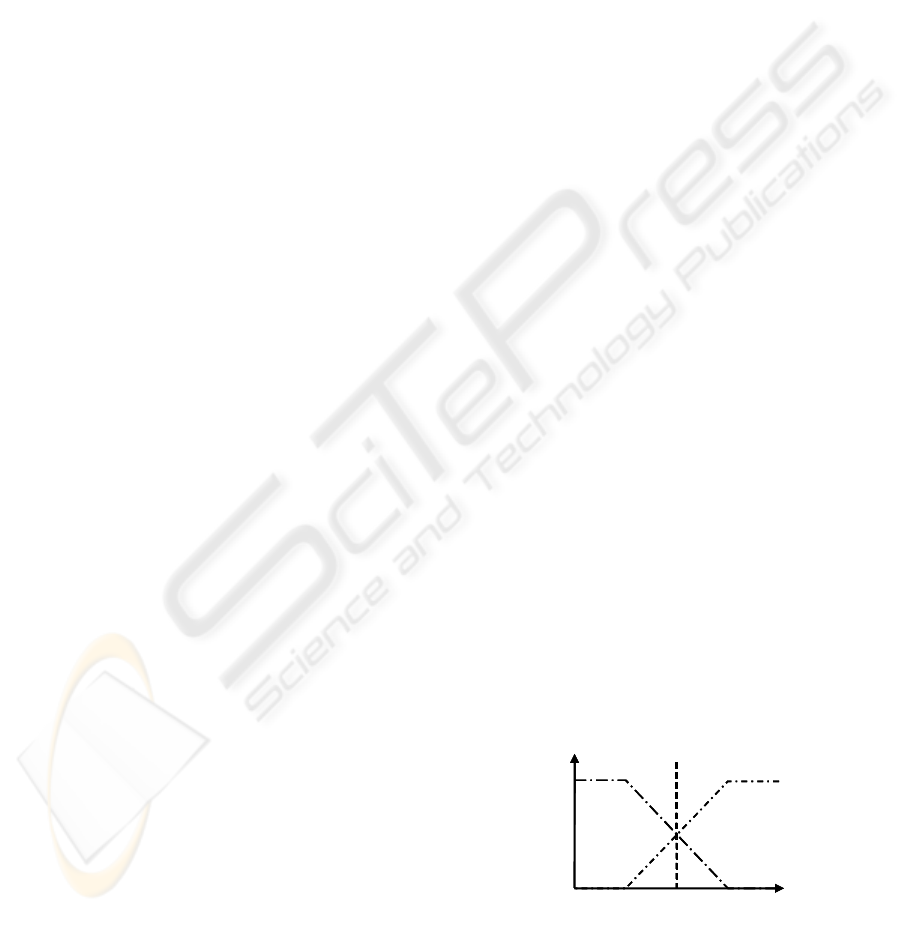
The indicator for similarity in fuzzy sets is called

membership degree µ=[0,…,1]. A membership

degree µ=1 indicates that an object fully belongs to a

set while a membership degree µ=0 shows a total

dissimilarity between an object and a set.

In our example, the customer with $ 1.1 million

may have membership degrees of e.g.

RICH

($1.1M)=0.6 to the set rich and

POOR

($1.1M)=0.4 to the set poor (Fig. 2). This

indicates that the customer is rich but not extremely

wealthy. However a person possessing $ 50 billions

would surely have memberships of µ

RICH

($1B)=1.0

and µ

POOR

($1B)=0.0.

Note that there is probabilistic uncertainty

neither about the fortune of the customer (he has $

1.1 million) nor about the rules for how to classify

him into one or other of the two sets (determined by

the functions given in Fig. 2). Therefore the

membership degrees do not indicate any probability

of belonging to the sets, but similarities of values to

those sets.

Membership Degree

1 Fortune [million $]0

Fuzzy Class:

Poor

Fuzzy Class:

Rich

Crisp

Separator

Figure 2: Fuzzy Concept

Membership Degree

1 Fortune [million $]0

Fuzzy Class:

Poor

Fuzzy Class:

Rich

Crisp

Separator

Figure 2: Fuzzy Concept

Figure 2: Fuzzy Concept.

FLEXIBLE COMPLETION OF WORKFLOW ACTIVITIES

175

Probability Concept

The same bank may face probabilistic uncertainty

about the wealth of a customer. For example, a new

customer driving up with an old bicycle might be

considered of having a fortune of , say, $ 10 while it

might be assumed that a customer chauffeured to the

bank in a big limousine could have a million dollars.

However, these are only the guesses of the bank

employees. The vehicles of the customers are

indicators for the wealth but no proof. Therefore the

bank clerks have to act under probabilistic

uncertainty. The biker could be a crazy billionaire

while the chauffeured customer might be a debt-

ridden conman.

The biker (BI) might have a fortune of $ 10 with

a probability of P

($10)=0.9 and a fortune of one

million dollars with a probability of P

($1M)=0.1

while the limousine customer (LI) has the following

probabilities: P

($10)=0.2 and P

($1M)=0.8.

Note, that in the example only probabilistic

uncertainty is taken into account. In contrast to the

fuzzy concept as shown in the previous section the

amounts of money ($ 10 and $ 1 million) are not

examined with respect to their similarity to the sets

poor and rich.

Joint Fuzzy and Probability Concept

Since the fuzzy and probability concepts are

independent they can be combined. For simplicity

let us consider here only the bike rider.

First the bank clerks estimate the fortune of the

new customers: the biker might have a fortune of $

10 with a probability of P

($10)=0.9 and a fortune

of one million dollars with a probability of

($1M)=0.1. Second the given amounts of money

are examined with respect to their similarity to the

sets rich and poor. Ten dollars may be classified

with the following membership degrees:

POOR

($10)=0.95 and µ

RICH

($10)=0.05. For one

million dollars we may get: µ

POOR

($1M)=0.02 and

RICH

($1M)=0.98.

Combining probably and fuzziness we finally

get: The biker belongs with a probability of P

=0.9

and to a membership degree of µ

POOR

=0.95 to the set

poor as well as to the set rich with µ

RICH

=0.05. With

a probability of P

=0.1 he belongs to the set rich

with a membership degree of µ

RICH

=0.98. as well as

to the set poor with µ

POOR

=0.02.

3.1.2 The Enhanced Finite State Models

The application of the fuzzy and probability

concepts leads to enhanced finite state models.

Fuzzy Enhanced Finite State Model

In a fuzzy enhanced finite state model (Fig. 3) the

similarity between the actual output of an activity

and a given post-condition is determined. A

membership degree µ=1 indicates that the output

fully satisfies the required post-condition while µ=0

shows a total dissimilarity between output and post-

conditions. Membership degrees between these

extreme values indicate partial compliance between

the actual output and the post-conditions.

The membership degrees can be utilized to

closed

aborted

sufficiently_completed (F

)

fully_completed

open

not_active

commence

active

scheduled

suspended

commenced

suspend

resume

partly_ completed:

N-1

Figure 3: Fuzzy Enhanced Activity Finite State Machine

closed

abortedaborted

sufficiently_completed (F

)sufficiently_completed (F

)

fully_completedfully_completed

open

not_active

commence

active

scheduled

suspendedsuspended

commenced

suspend

resume

partly_ completed:

N-1

Figure 3: Fuzzy Enhanced Activity Finite State Machine

Figure 3: Fuzzy Enhanced Activity Finite State Machine.

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

176

describe the states of completion in a more detailed

way than in the basic model as introduced in Section

2.2. The states can be added by a label F

≤ F

≤

1) which indicates the level of completion of the

activity: closed.completed (F

). Obviously the label

equals the membership degree of the actual output to

the post-condition as defined above. An activity with

the state closed.completed (0.8) shows that it

belongs to the set completed with a membership

degree of µ=0.8.

Furthermore we suggest explicitly distinguishing

between fully and only partly completed activities.

So we finally get the following states:

• state: closed.completed (F

) with F

≤ F

<1.0:

sufficiently_completed (F

)

• state: closed.completed (F

) with F

=1.0:

fully_completed

This leads to the fuzzy enhanced activity finite

state machine as shown in Fig. 3. The fuzzy

enhanced model now clearly separates the levels of

completion and therefore has a finer granularity in

comparison to the model of Lin and Orlowska.

Furthermore fuzzy set operators now easily allow

us to aggregate multi-dimensional post-conditions.

Let us extend our example of Section 3.1.1. Besides

the vehicles the bank clerks also take into account

the number of credit cards the new customer

presents to the bank. Zero credit cards would result

in a membership degree of µ

RICH

(CC=0)=0 to the set

while ten credit cards lead to µ

RICH

(CC=10)=1.

A customer possessing one million dollars and

seven credit cards then has the following

membership degrees: µ

RICH

($1M)=0.98 and µ

RICH

(CC=7)=0.7. To obtain the membership degree of

the combined decision the single memberships can

be summed up by a fuzzy aggregation operator, for

example the basic min-operator: µ

aggregated

=min{0.98,

0.7}=0.7.

Note, that the basic min-operator has no

compensatory power. E.g. Hamacher (1978)

introduced a class of intersection operators with

compensatory power:

))x()x()x()x()(1(

)x()x(

μμ−μ+μγ−+γ

μμ

=μ

∩

More compensatory operators can be found in

e.g. Dubois, Prade (1982), Werners (1988), Yager

(1980) or Zimmermann, Zysno (1980).

The introduction of the fuzzy sets leads to a

finite state model quite similar to that suggested by

Lin and Orlowska (also note the relationship to

fuzzy Petri Net approaches e.g. Rapso et al. (2001))

The main advantage is that one can use this well

established theory with its tools to formulate the

partial completeness of the activities.

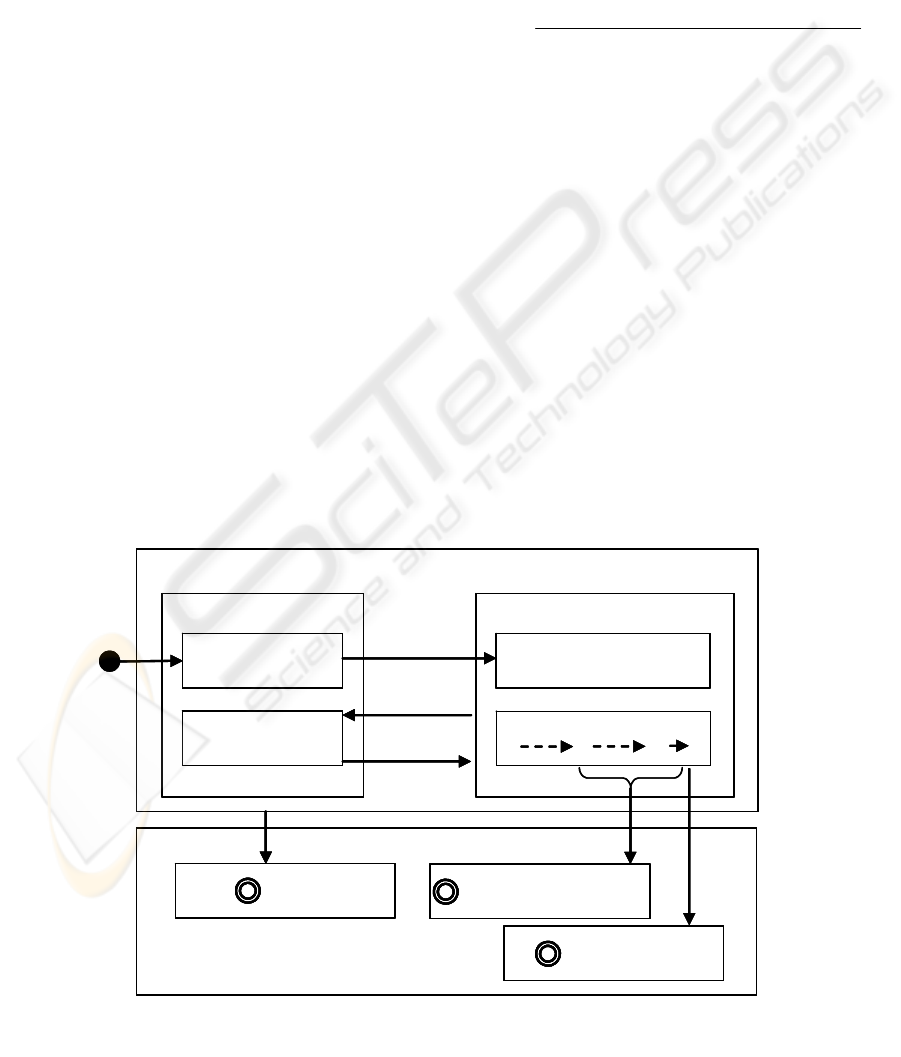
Probabilistically Enhanced Finite State Model

The probabilistically enhanced finite state engine

(Fig. 4) deals with the probabilistic uncertainty over

whether or not the outcome actually matches the

intended post-conditions of the activity.

In our example the bank clerks have to decide

under probabilistic uncertainty whether the

approaching customer is rich or poor. Generally they

have two different policies when their decision turns

out to be wrong (e.g. the limousine customer has no

closed

aborted

probably_completed (P

)

surely_completed

open

not_active

commence

active

scheduled

suspended

commenced

suspend

resume

partly_ completed:

N-1

Figure 4: Probabilistically Enhanced Activity Finite State Machine

closed

abortedaborted

probably_completed (P

)probably_completed (P

)

surely_completedsurely_completed

open

not_active

commence

active

scheduled

suspendedsuspended

commenced

suspend

resume

partly_ completed:

N-1

Figure 4: Probabilistically Enhanced Activity Finite State Machine

Figure 4: Probabilistically Enhanced Activity Finite State Machine.

FLEXIBLE COMPLETION OF WORKFLOW ACTIVITIES

177

money at all):

• Policy 1. The bank clerks do not revise their

decision and continue to service the customer as

if he were rich: e.g. an approval for a home loan

will not be withdrawn. The process continues

memory-free, that means that once a decision is

taken it will never be corrected. The workflow

system does not require any roll-back strategies.

• Policy 2. The drive up with the limousine is

accepted only as first proof for wealth. The

customer gets an approval for a home loan

under the reserve that he proves to be rich

within a given time period. Here the workflow

system needs roll-back strategies in case that the

customer turns out to be poor. This policy needs

an advanced transaction management (e.g.

Leymann, Roller 2000).

To distinguish between a surely completed

activity and an activity that is only completed with a

certain probability the following states are

introduced:

• state: closed.completed (P

) with P

≤ P

<1.0:

probably_completed (P

)

• state: closed.completed (P

) with P

=1.0:

surely_completed

The nomenclature parallels the one we have

already presented for the fuzzy dimension. The

corresponding probability enhanced activity finite

state machine is show in (Fig. 4).

Along the lines of the discussion on fuzzy trade-

offs we introduce a compensation between outcomes

on different levels of certainty or probabilistic

uncertainty. Now, in our example the vehicles as

well as the credit cards are taken into account.

The biker (index BI)has a probability of

($10)=0.9 that he owns $ 10 (see above).

However he possesses ten credit cards (index CC)

which leads to a following probability of

($10)=0.2 that he owns $ 10 and P

(1M)=0.8

that he has one million dollars. For simplicity’s sake

let us assume that the probabilities related a) to the

vehicle and b) to the number of credit cards are

statistically independent. Then the overall

probability that he has $10 is: P

($10)*

($10)=0.18.

Fuzzy and Probabilistically Enhanced Finite

State Model

As discussed above the fuzzy and probability

dimensions are independent from each other.

Therefore they can be combined. The resulting

probabilistic-fuzzy completion states can be derived

straightforwardly from the models introduced in the

previous Sections. They are defined as follows:

• state: closed.completed (F

, P

) with (F

≤F

and

≤P

) and (F

<1.0 and/or P

<1.0):

sufficiently_completed (F

, P

)

• state: closed.completed (F

, P

) with F

=1.0 and

=1.0: fully_completed

3.2 Processes with Memory

Up to now we have considered a memory-free

process: the level of completion of an earlier activity

(process step) is not recorded and therefore has no

influence on any later process step. In particular no

compensation between process steps is possible.

However, we have already introduced the

possibility of fuzzy and probabilistic compensations

within one process step (in our example between the

kind of vehicle and the number of credit cards). We

can easily generalize this construct to compensations

between different process steps (activities) by

introducing a process memory. In such a generalized

model the degree of completion has an impact on

future decision spaces within the process.

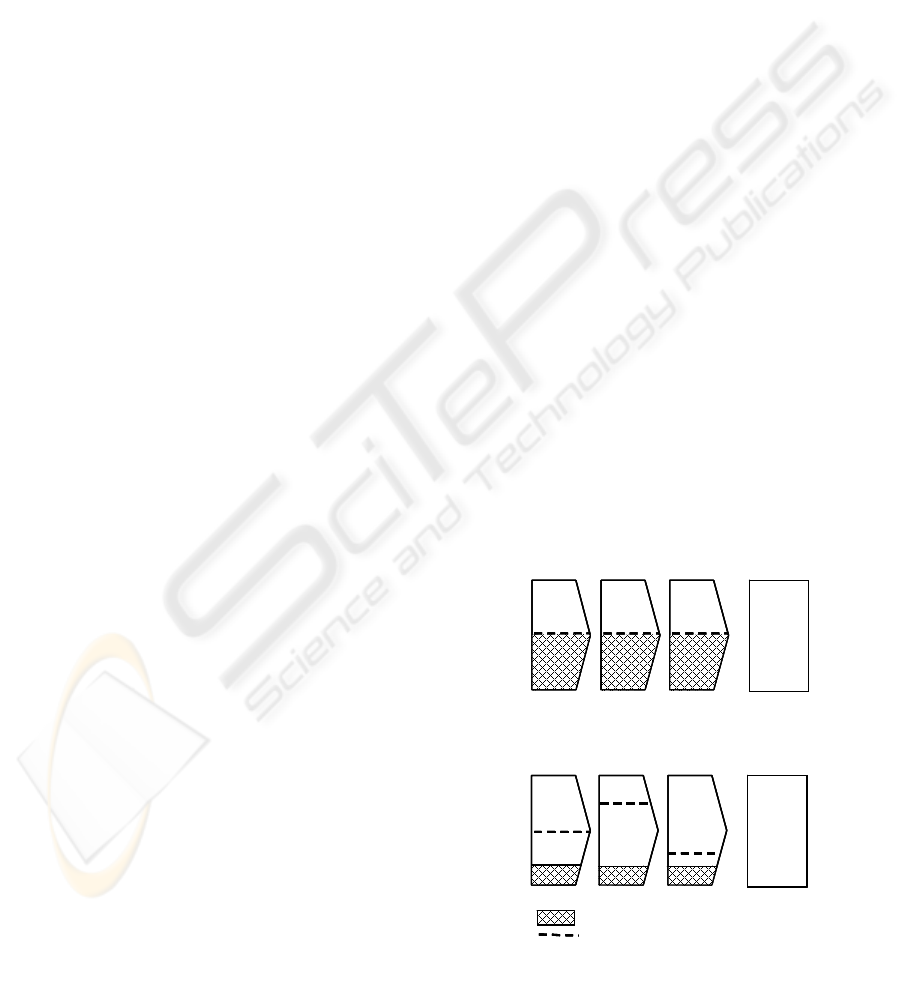
A. Memory-free Process:

Minimum Requirement for each Activity:

5 out of 10

B. Process with Memory:

Minimum Requirement for each Activity:

2 out of 10

Minimum Requirement

Actual Level of Competition

Level of

Completion: 15

Level of

Completion: 15

555

Figure 5: Process Memory

A. Memory-free Process:

Minimum Requirement for each Activity:

5 out of 10

B. Process with Memory:

Minimum Requirement for each Activity:

2 out of 10

Minimum Requirement

Actual Level of Competition

Level of

Completion: 15

Level of

Completion: 15

555

A. Memory-free Process:

Minimum Requirement for each Activity:

5 out of 10

B. Process with Memory:

Minimum Requirement for each Activity:

2 out of 10

Minimum Requirement

Actual Level of Competition

Level of

Completion: 15

Level of

Completion: 15

555

Figure 5: Process Memory

Figure 5: Process Memory.

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

178

In a memory-free process every step of the

process must meet minimum requirements

independently from the other process steps (Fig.

5A). Once the minimum requirements of an activity

are met the process owner is free to define it as

completed and continue with the next activity. The

overall objective of the process can only be taken

into account indirectly since no trade-off between

the levels of completion of the single activities is

possible. In the case of a memory-free process one

always has to assume the worst case scenario - this

is when all activities just reach their minimum

requirements. However these minimum

requirements must meet higher standards in

comparison to a process with memory where

compensations between high and low performing

activities are possible (Fig. 5B).

When only one activity is completed on a higher

level then the process objective is also accomplished

at a higher degree than needed. Generally this leads

to a waste of resources and a reduced flexibility in a

memory-free process. In the process shown in Fig.

5B for example, the good performances of the

process in the first two steps allow the last activity to

completed on a low level without endangering the

overall process output.

The increased flexibility of a process with

memory in comparison to a memory free process is

counterbalanced by the following drawbacks:

• Processes with memory can only applied when

trade-offs between the objectives of the

activities are present. In particular, designing

such a process is more complex than designing

a memory-free process since the trade-offs must

be specified. In the running phase the workflow

system must additionally monitor and record the

degrees of completion of each activity.

• The possible trade-off between low and high

accomplishment of activities might encourage

performers of early activities to meet only the

minimum requirements. This could result in

stricter requirements and less flexibility in later

process steps (even stricter than in a process

without memory). However it could be more

likely that the later process steps require greater

flexibility than the earlier ones.

Therefore the use of such processes needs to be

carefully deliberated to ensure that the performance

meets the expectations of the process owner.

4 CONCLUSION

In this paper we extended the concept of partly

complete-able activities by distinguishing two

independent dimensions (fuzziness and probability)

and introducing a process memory. The two

dimensions allow us to describe the reasons for the

partial completion of activities in more detail. The

process memory allows us to formulate trade-offs on

the level of completion between earlier and later

activities, and make it easier to meet the overall

process goal in comparison to a memory-free

approach.

Both our extensions lead to an increase in

process flexibility in comparison to the approach of

Lin and Orlowska and classic workflow systems.

However partly complete-able workflow systems

(both fuzzy and probabilistic) with memory require

very detailed information in the design phase to

customize the levels of completion and the trade-offs

between the activities. This information would be

very difficult to determine in real life. Therefore it

will be difficult to implement - and economically

operate - such a workflow system in the near future.

However in the longer term, further progress in

artificial intelligence and automated learning might

provide methods to overcome these obstacles.

Our opinion is that these compensation structures

and process memory are very common when

humans conduct any kinds of processes that are not

supported by information technology. Therefore we

think that it is important to recognize and describe

these phenomena, since they might provide reasons

why an IT-supported workflow may not perform in

the expected way. Knowing the reasons might

provide strategies for workarounds until more

sophisticated, human like, technologies are

developed to further bridge the gap between

technology and human thinking.

REFERENCES

Carter, B.M.; Lin, J.Y.C; Orlowska, M.E., 2004:

Customizing Internal Activity Behaviour for Flexible

Process Enforcement. Proceed. 15th Australasian

Database Conference, Dunedin, New Zealand

DSTC Praxis Project 2004: Chameleon Website,

www.dstc.edu.au/Research/Projects/praxis/

chameleon/index.html

Dubois, D.; Prade, H., 1982: A class of fuzzy measures

based on triangular norms. International Journal of

General Systems, 8, 43-61

FLEXIBLE COMPLETION OF WORKFLOW ACTIVITIES

179

Hamacher, H., 1978: Ueber logische Aggregationen nicht-

binaer expliziter Entscheidungskriterien. Rita G.

Fischer Verlag, Frankfurt, Main, Germany

Klir, G., 1989: Is there more Uncertainty than some

Probability Theorist might have us believe?

International Journal of General Systems, 15, 347-378

Leymann, F.; Roller, D., 2000: Production Workflow:

Concepts and Techniques. Prentice-Hall, Upper

Saddle River, NJ, USA

Lin, J.Y.C.; Orlowska, M.E., 2005: Partial completion of

activity in business process specification. Proceed.

IRMA 2005, San Diego, CA, USA, 186-189

Raposo, A.B.; Coelho, A.L.V.; Magalhães, L.P.; Ricarte,

I.L.M., 2001: Using Fuzzy Petri Nets to Coordinate

Collaborative Activities. Proceed. 9th IFSA World

Congress & 20th NAFIPS Intern. Conf., Vancouver,

Canada, 1494-1499

Reichert, M.; Dadam, P., 1998: ADEPTflex - supporting

dynamic changes of workflows without losing control.

Journal of Intelligent Information Systems, 10, 93-129

Sadiq, S. 2000: Handling Dynamic Schema Change in

Process Models. www.dstc.edu.au/

Research/Projects/praxis/publications/ssadiq_adc_200

0.pdf (accessed 08.07.2005)

Tagg, R.M. 2003: Dimensions of Flexibility in Workflow

Management, EURO/INFORMS Conference, Istanbul,

2003

van der Aalst, W.; van Hee, K. 2002: Workflow

Management - Models, Methods, and Systems. MIT

Press, Cambridge, MA, USA

Werners, B. 1988: Aggregation models in mathematical

programming. In Mitra, G.: Mathematical Models for

Decision Support. Springer Verlag, Berlin, 295-319

Workflow Management Coalition 1995: Workflow

Management Coalition - The Workflow Reference

Model. Doc. # WFMC-TC1003

Yager, R.R. 1980: On a general class of fuzzy

connectives. Fuzzy Sets and Systems, 4, 235-242

Zadeh, L. 1965: Fuzzy Sets. Information and Control, 8,

338-353

Zadeh, L. 1983: Is Possibility different from Probability?

Human Systems Management, 3, 253-254

Zadeh, L. 1995: Probability Theory and Fuzzy Logic are

Complementary Rather Than Competitive.

Technometrics, 37, 271-276

Zimmermann, H.J. 2001: Fuzzy sets and its applications

edition). Kluwer Academic Publishers, Boston,

MA, USA

Zimmermann, H.J.; Zysno, P. 1980: Latent connectives in

human decision making. Fuzzy Sets and Systems, 4,

37-51

ICEIS 2006 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

180