KNOWLEDGE-BASED MODELING AND NATURAL COMPUTING

FOR COORDINATION IN PERVASIVE ENVIRONMENTS

Michael Cebulla

Technische Universit

at Berlin, Institut f

ur Softwaretechnik und Theoretische Informatik,

Franklinstraße 28/29, D-10587 Berlin,

Keywords:

Knowledge Engineering, Coordination in Multi-Agent Systems, Systems Engineering Methodologies.

Abstract:

In this paper we start with the assumption that coordination in complex systems can be understood in terms of

presence and location of information. We propose a modeling framework which supports an integrated view

of these two aspects of coordination (which we call knowledge diffusion). For this sake we employ methods

from ontological modeling, modal logics, fuzzy logic and membrane computing. We demonstrate how these

techniques can be combined in order to support the reasoning about knowledge and very abstract behavioral

descriptions. As an example we discuss the notion of distributed action and show how it can be treated in

our framework. Finally we exploit the special features of our architecture in order to integrate bio-inspired

coordination mechanisms which rely on the exchange of molecules (i.e. uninterpreted messages).

1 INTRODUCTION

Enabled by the recent advances on the ﬁelds of hard-

ware design, wireless communication and (last not

least) the Internet the distribution of mobile devices

in society will dramatically increase during the forth-

coming decade. In these pervasive environments es-

pecially the requirement of context-awareness is crit-

ical: mobile devices have to be aware of information

and services which are present in the current situation

and cooperate with them when desirable. On the other

hand they are also required to provide meaningful be-

havior when these services cannot be found. Conse-

quently pervasive systems have to possess novel inter-

action capabilities in order to be aware of the current

situation and to initiate adequate behaviors. These ca-

pabilities are key features for the success of emerg-

ing pervasive technologies and are discussed under

the topic autonomous computing (Kephart and Chess,

2003).

In this presentation we focus on the systems’ abil-

ity to initiate cooperations with other systems and to

represent knowledge about themselves and their sit-

uation. As we will see a special focus lies on is-

sues related to the locality of knowledge and on the

migration of information. We treat the ﬁrst aspect

of knowledge representation by relying on ontologi-

cal modeling and knowledge bases thus enabling the

high-level modeling of complex systems (as already

proposed by (Pepper et al., 2002)). Regarding the

second aspect related to the migration of knowledge

we rely on membrane computing (P

aun, 2000). This

model which was taken from biology is highly ap-

propriate to model systems which have to interact ex-

tensively with their environment. Systems which are

modeled by membranes have porous system borders

where molecules can intrude and exit. As we will see

these molecules can be used to represent information

which diffuses through the system.

For the syntactic representation of knowledge we

propose to use ontologies (i.e. description logics

(Baader et al., 2003)) as a light-weight formalism

which provides support for automated reasoning.

From our point of view such a formalism meets some

requirements which may be unfamiliar from a tradi-

tional viewpoint concerning system modeling.

Intelligibility. Since it is very close to natural lan-

guage and thus supports the direct usage of

domain-speciﬁc terminology, ontological modeling

provides an instrument for a seamless knowledge

management.

Uncertainty and Incompleteness. Systems in ad-

verse environments are subject to unexpected inﬂu-

ences (uncertainty) and are characterized by a high

complexity which makes an exact description im-

possible or inefﬁcient. As we will see the issues of

Cebulla M. (2006).

KNOWLEDGE-BASED MODELING AND NATURAL COMPUTING FOR COORDINATION IN PERVASIVE ENVIRONMENTS.

In Proceedings of the Eighth Inter national Conference on Enterprise Information Systems - AIDSS, pages 99-106

DOI: 10.5220/0002454500990106

 SciTePress

vagueness and uncertainty are treated by the intro-

duction of fuzzy logics (Klir and Yuan, 1995) and

modal logics (Wooldridge, 1992) into terminologi-

cal reasoning.

Highly Reactive Behavior. Since the semantics of

membrane computing is based on multisets it is

well-suited for the treatment of highly reactive be-

havior since e.g. inadequate assumptions concern-

ing sequentiality are avoided.

Efﬁcient Automated Reasoning. We claim that an

enhanced intelligibility and support for incomplete

speciﬁcations have to go hand in hand with well-

deﬁned semantics and efﬁcient decision proce-

dures. A standard way of reasoning is provided

procedures which are based on tableau algorithms

(Baader et al., 2003) which support a smooth inte-

gration of different aspects of knowledge. A key

issue in this context is the adequate treatment of

implicit information, e.g. with respect to structural

similarities of different entities. Such a treatment is

possible by exploiting the concept of subsumption

as deﬁned in the context of description logics.

This paper is organized as follows: ﬁrst we give

an outline of the general architecture (cf. Sec-

tion 2). In this section we discuss the signiﬁcance of

observation-based behavioral modeling (cf. Subsec-

tion 2.1) and brieﬂy introduce the basic concepts from

membrane computing (cf. Subsection 2.2). Then we

brieﬂy discuss the basic concepts of fuzzy descrip-

tion logics (cf. Subsection 2.3). Section 3–4 give an

overview about terminological reasoning concerning

exemplary system aspects (e.g. architecture and be-

havior). We then show how to treat abstract speciﬁca-

tions of distributed actions in our framework (cf. Sec-

tion 5). Sections 4 and 5 can be considered as an

exemplary discussion of tableau-based reasoning in

the medium of membrane computing. In Section 6

we ﬁnally give an example for the integration of bio-

inspired coordination supported by our framework.

Throughout the paper we use examples from disas-

ter management because we feel that the challenges

related to context-awareness are very speciﬁc in these

area.

2 GENERAL ARCHITECTURE

As we already indicated we doubt that traditional in-

teraction mechanisms (like procedure calls or mes-

sage passing) are qualiﬁed to support context-aware

behavior in pervasive environments. For this reason

we employ methods from the ﬁeld of natural com-

puting which are better suited to support the analysis

of knowledge diffusion. Since we refer to mechanisms

which were originally observed in biological or social

read/write

Environment

isponent

Sensor

In the near future I will

have to talk to a local

officer−in−charge (e.g. via GSM)

Probably the antenna−pole

will be flooded within three hours

Figure 1: Typical Coordination Problem.

environments we start with examples from so-called

socio-technical systems (e.g. coordination in disaster

management). In this section we discuss a motivating

example and develop the basic architecture.

2.1 Observation-based Modeling

We select disaster management as one of our target

domains because there in the typical case the situa-

tion is characterized by high environmental dynam-

ics, high need of information and frequent coordina-

tion problems. Obviously in this scenario (cf. Fig-

ure 1) the water-level is a highly important informa-

tion (since it is one of the main parameters of the

ﬂooding). Thus it surely makes sense to observe this

parameter and keep track of its changes. This is com-

monly done by sensors (which are represented by an

unique sensor in our simpliﬁed architecture). Sensors

collect information which then can be sent to the parts

of the system where decisions are made on the basis

of this information (e.g. the disponent). So far an ini-

tial model. But the real situation is far more complex.

In fact the behavior of the ﬂood (and thus the para-

meter water-level) cannot be considered as an isolated

phenomena which can be observed by an independent

observer. On the contrary the evolution of the situa-

tion (the ﬂooding) directly affects the internals of sys-

temic communication and decision making. Thus the

rising of a ﬂood has frequently severe consequences

for the infrastructure (e.g. telephone nets for conven-

tional or mobile communication). This dependency

may lead to complex and hidden interactions between

systemic aspects which seem to be unrelated at ﬁrst

sight. For instance the rising of the ﬂood interacts

with the disponent’s need to use mobile telecommuni-

cation in the near future when an antenna pole will not

be operable due to overﬂooding. Note that such hid-

den interactions between components are known as

complex interactions (Leveson, 1995; Perrow, 1984)

and are considered as major causes for losses and ac-

cidents.

Agents Knowledge and Behavior. We consider

our approach as an extension of the modeling of

multi-agent systems (cf. for example (Fagin et al.,

1996)). For reasoning about knowledge and behavior

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

100

Officer−

in−Charge

Disponent

water−level.=0.7

Sensor

Environment

antenna−pole.intact

Figure 2: Scenario from Disaster Management (simpliﬁed).

we presuppose that each agent supports the following

interface.

interface Agent

know: X × T → bool

next: X × T → X

Such a signature is especially suited for the model-

ing of black box-behavior. While the function know

supports observations concerning the current state of

an agent the function next supports experiments con-

cerning the behavior of an agent. Note that these func-

tions have some coalgebraic ﬂavour since the state

space X of an agent may not be known completely

(cf. (Rutten, 1996)). Thus these functions support the

reasoning about an agent’s state (his knowledge) and

his behavior without requiring information about his

internals.

While the agent-interface supports the observation

of agents their real behaviors are described with con-

cepts from membrane computing (cf. Subsection 2.2).

Consequently, each agent is considered to be enclosed

by a membrane. As we will see, due to this fact infor-

mation can diffuse through systems and agents bor-

ders according to diffusion rules. We use concepts

from multiset rewriting in order to describe the diffu-

sion of knowledge through complex systems.

In Figure 2 we show some relevant agents in an

highly simpliﬁed scenario of coordination described

by our example. We show how to model agents as

locations of information. We consider the knowledge

which is situated inside the membranes as private to

the agents while the information which is outside is

accessible to all agents which share a certain environ-

ment.

Discussion. We can make several observation us-

ing this example. Firstly we claim that problems

of this type can be modeled using the paradigm of

knowledge diffusion. An important notion in this con-

text concerns the location of information and question

whether this location is suitable for this information

or if it has to be moved to other locations. In addi-

tion we have to provide advanced coordination mech-

anisms which are highly robust in order to be able

to process for example the tight connection between

environment and communication. Consequently we

propose to use the paradigm of knowledge diffusion

not only for the analysis of coordination problems

but also as a platform for very robust coordination.

The related processes of knowledge diffusion are very

similar to processes of biological knowledge process-

ing (e.g. the usage of pheromones in insect popula-

tions, cf. (Krasnogor et al., 2005)).

Environment. Obviously in our approach the en-

vironment plays a prominent role. For illustration we

distinguish two characteristic scenarios.

Naive Scenario. In the naive scenario the environ-

ment takes an adversial role. It does not pro-

vide knowledge about the situation but disturbs the

agents’ actions deliberately. The relevant knowl-

edge is located exclusively in the agents. The

weakness of this model consist in the fact that this

knowledge does not sufﬁce in complex and dy-

namic setting. Thus the agents have to specify in-

teractions on the basis of incomplete knowledge.

For example this will lead him to an inadequate se-

lection concerning the communication channel.

Intelligent Environment. In the second case the en-

vironment incorporates relevant situational knowl-

edge which can be used in order to enhance the

systems behavior. The agents possess only incom-

plete knowledge about the situation. Consequently

most of their actions have to be considered as inter-

actions with the environment. The agents initiate

only very abstract interactions while the environ-

ment is in charge to introduce the missing informa-

tion. We consider this interaction with assistance

by an intelligent environment as a typical case of

knowledge diffusion. In this scenario agents do not

address certain services but just give an expression

of their needs to the environment.

The naive scenario perfectly describes the tradi-

tional view on systems which are not context-aware.

In these systems the relevant knowledge is situated

in the agents while the environment is considered to

be adversial. In the case of intelligent environments

on the other hand each action of an agent has to be

considered as a joint action (also called distributed

action) which is performed in cooperation with the

environment.

2.2 Membrane Computing

More formally we represent knowledge as molecules

(or terms) which are contained in multisets. The dif-

fusion of knowledge can thus be described by multiset

rewriting. For example, the diffusion of information

in systems can described by simple rules:

[water-level.High] → [(need-to-act, out)]

In this notation we use the brackets [ and ] for the

speciﬁcation of the membrane structure. In our ex-

KNOWLEDGE-BASED MODELING AND NATURAL COMPUTING FOR COORDINATION IN PERVASIVE

ENVIRONMENTS

101

ample the brackets delimit the multiset which repre-

sents the knowledge which is private to the sensor.

The resulting rule describes the distribution of infor-

mation through the system. We deliberately use inex-

act terms like need-to-act in order to demonstrate the

possibilities of high-level modeling. By the standard

action out we specify that this molecule has to exit

the sensor’s local state. Note that this molecule is not

expected to carry extensive semantic signiﬁcance but

may only transmit the information that the system’s

current state is not optimal.

P-Systems. Following (P

aun, 2000) we use the

concept of P systems which heavily relies on the

metaphor of a chemical solution (Berry and Boudol,

1992) for the representation of knowledge in a sys-

tem. As we already saw a solution contains molecules

which represent terms. As we will see these terms are

elements of a language which is describe by an on-

tology. More formally a P-System can be deﬁned as

follows (slightly adapted from (P

aun, 2000)):

Deﬁnition 1 (P-System) A P-system of

degree m is deﬁned as a tuple Π=

O, µ, w

,...,w

,...,R

, where O is an

ontology, µ is a membrane structure, w

,...,w

are multisets of strings from O (representing the

knowledge contained in regions 1, 2,...,m of

µ, R

,...,R

are sets of transformation rules

associated with the regions.

We chose this highly reactive semantic model as the

basis of our process description because we feel that

it is highly appropriate for the description of unex-

pected behavior. Especially, environmental changes

or unexpected contextual inﬂuences can be modeled

by introducing new molecules into the solution. In

addition no assumptions concerning artiﬁcial sequen-

tiality are imposed on the events contained in a mul-

tiset: in general case they can occur in every possible

order.

2.3 Fuzzy Description Logics

For the representation of terms which may be sub-

ject to semantic interpretation we use fuzzy descrip-

tion logics. Following (Straccia, 2001) we introduce

semantic uncertainty by introducing multi-valued se-

mantics into description logics. Consequently we

have to introduce fuzzy sets (Zadeh, 1965) instead

of the crisp sets used in the traditional semantics (cf.

(Baader et al., 2003)). For this sake we conceive the

model of the terminological knowledge which is con-

tained in a knowledge base as fuzzy set. When used

in assertional statements we can express the fact that

different instances (elements of ∆) may be models of

a concept to a certain degree.

Deﬁnition 2 (Fuzzy Interpretation) A fuzzy inter-

pretation is a pair I =(∆

, ·

), where ∆

is, as

for the crisp case, the domain whereas ·

is an inter-

pretation function mapping

1. individuals as for the crisp case, i.e. a

= b

, if

a = b;

2. a concept C into a membership function C

∆

→ [0, 1];

3. a role R into a membership function R

:∆

∆

→ [0, 1].

If C is a concept then C

will be interpreted as the

membership degree function of the fuzzy concept C

w.r.t. I. Thus if d ∈ ∆

is an object of the domain

∆

then C

(d) gives us the degree of being the ob-

ject d an element of the fuzzy concept C under the

interpretation I (Straccia, 2001).

In this article we make use of the usual operators

from description logics and silently introduce predi-

cates on fuzzy concrete domains (which are very sim-

ilar to linguistic variables and support the integra-

tion of linguistic hedges (Klir and Yuan, 1995)). We

also heavily rely on the concept of fuzzy subsumption

which we introduce by example. In addition we intro-

duce complex role-terms in Section 5. Unfortunately

we are not able to give an extensive treatment due to

space limitations.

Fuzzy Subsumption. Intuitively a concept is sub-

sumed by another concept (in the crisp case) when

every instance of the ﬁrst concept is also an instance

of the second. In the fuzzy case, however, we are in-

terested in the degree to which the current situation

conforms to a certain concept. As an example we

consider a case from the domain of disaster manage-

ment. In the following we are interested in the degree

to which a current-situation can be considered as a

ﬂooding.

ﬂooding

= sit ∃water-level.very(High)

curr-sit

= sit ∃water-level. =

On this background we can reason about the fol-

lowing statement:

KB |≈

deg

curr-sit  ﬂooding

Intuitively we can give a visual account of the ar-

gumentation related to the problem (cf. Figure 3). For

the linear representation of very we use:

very(x)=



x :0<x<0.75

2x − 1:0.75 ≤ x ≤ 1

As as solution we obtain a support of .33 for the de-

gree to which the description of the current situation

is subsumed by the concept ﬂood. We argue that this

kind of request may be a typical case concerning the

knowledge based support of context-awareness.

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

102

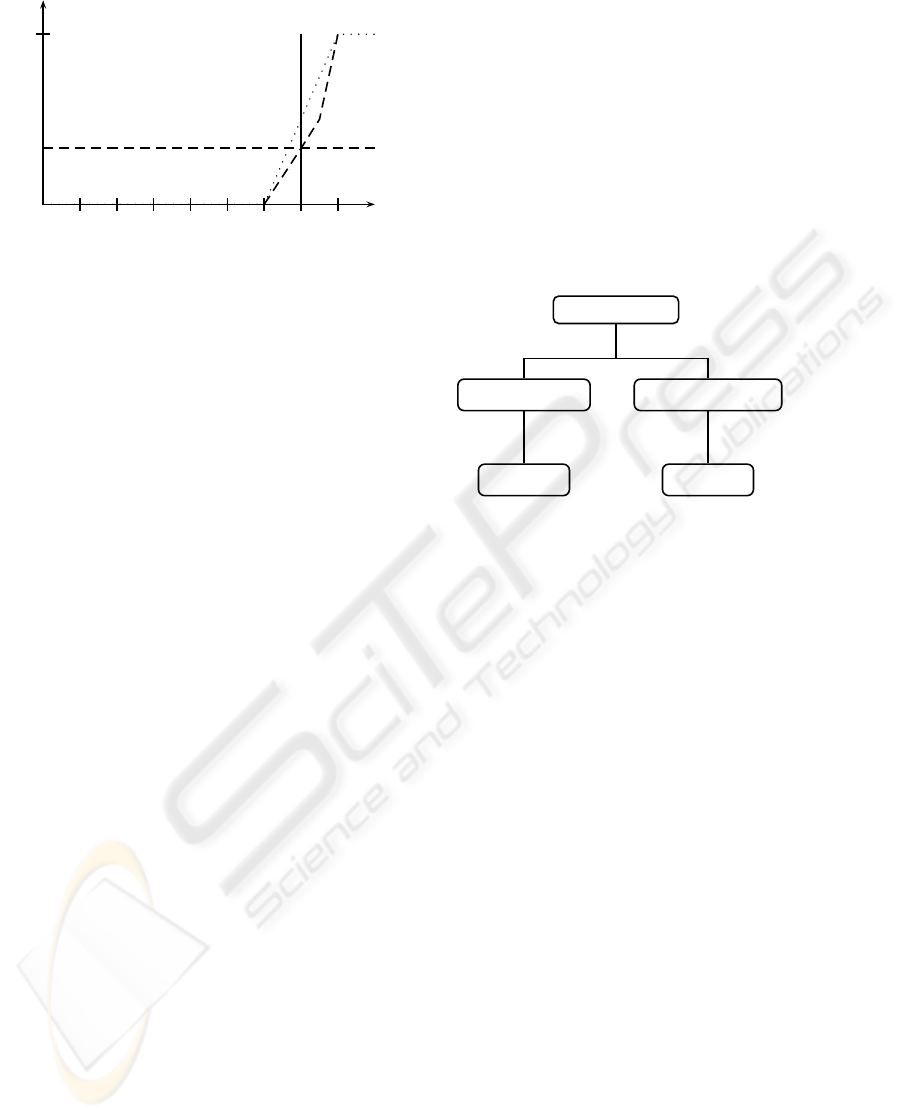
12345678

.33

Figure 3: (Very) High.

agent

= ∃ water-level. =

0.7

Figure 4: Terminological Representation of an Agent’s

State.

3 KNOWLEDGE

In our approach a system’s current state is represented

in terms of knowledge and its location. On this back-

ground we can demonstrate the inﬂuences of knowl-

edge on the agents actions and the effects of these

actions on the distribution of knowledge. Consider-

ing our running example again it becomes clear that

knowledge about the environment (e.g. communica-

tion paths (or channels) has to be available when initi-

ating a communication act. As we already saw in Sub-

section 2.1 this knowledge may located in the agent

or in the environment. In this section we discuss the

question how such knowledge is represented and in

which way it can be accessed.

Agents. In our approach agents are modeled as P-

systems. Thus their state is represented by regions

and their knowledge by ﬂoating molecules. Since we

conceive these terms as assertions related to an ontol-

ogy we can use predeﬁned complex concepts in order

to represent an agent’s state. In Figure 4 we show

a simple representation of an agents state. In this

case the agent’s state is characterized by the aware-

ness concerning the water level.

Note that this kind of representation is not acces-

sible for our observation-based approach in which

agents are treated as black-boxes. Following this

maxim of strict encapsulation we have to rely ex-

clusively on the observation functions know and next

in order to get information about knowledge and be-

havior. Note that this approach supports the formal

treatment of highly abstract characteristics of behav-

ior which are independent of individual details of cer-

tain agents.

In order to retrieve some information about the in-

= Communicate

= Conn-by-Conv

= Conn-by-Mobile

= Msg-Sent

∃select-conv.s

∃select-mobile.s

∃send.s

Figure 5: Terminological Description of States and Transi-

tions.

Communicate

Conn-by-Conv

select-conv

Msg-Sent

send

Conn-by-Mobile

select-mobile

Msg-Sent

send

Figure 6: Example: Behavioral Description.

ternal state of the agent we have to use the observa-

tion function know in a way which is very similar to

requests to knowledge bases.

know

ag ent

(∃water-level.High), 0.33

4 BEHAVIOR

For the representation about behavior we ex-

ploit the correspondence between description log-

ics and propositional dynamic logic (ﬁrst published

by (Schild, 1991)). This allows us to reuse the same

syntactic concepts (which we used for knowledge rep-

resentation in Section 3) for description of behav-

iors. Intuitively we use concepts for the description

of states while roles represent events which initiate

state transitions. As an example we give a simpliﬁed

description of the behavior in our example in Figure 5.

In order to support intuitive reasoning about behav-

ioral description we rely on simple a visual notation

(cf. Figure 6). In this notation the nodes of a tree rep-

resent states. The soft boxes contain (possibly com-

plex) concepts which have to hold in the particular

state. Edges are labeled with names of events (repre-

sented by role names).

Conformance. When reasoning about systems be-

havior an essential question is whether a given agent

is able to conform to a behavioral description. Again

KNOWLEDGE-BASED MODELING AND NATURAL COMPUTING FOR COORDINATION IN PERVASIVE

ENVIRONMENTS

103

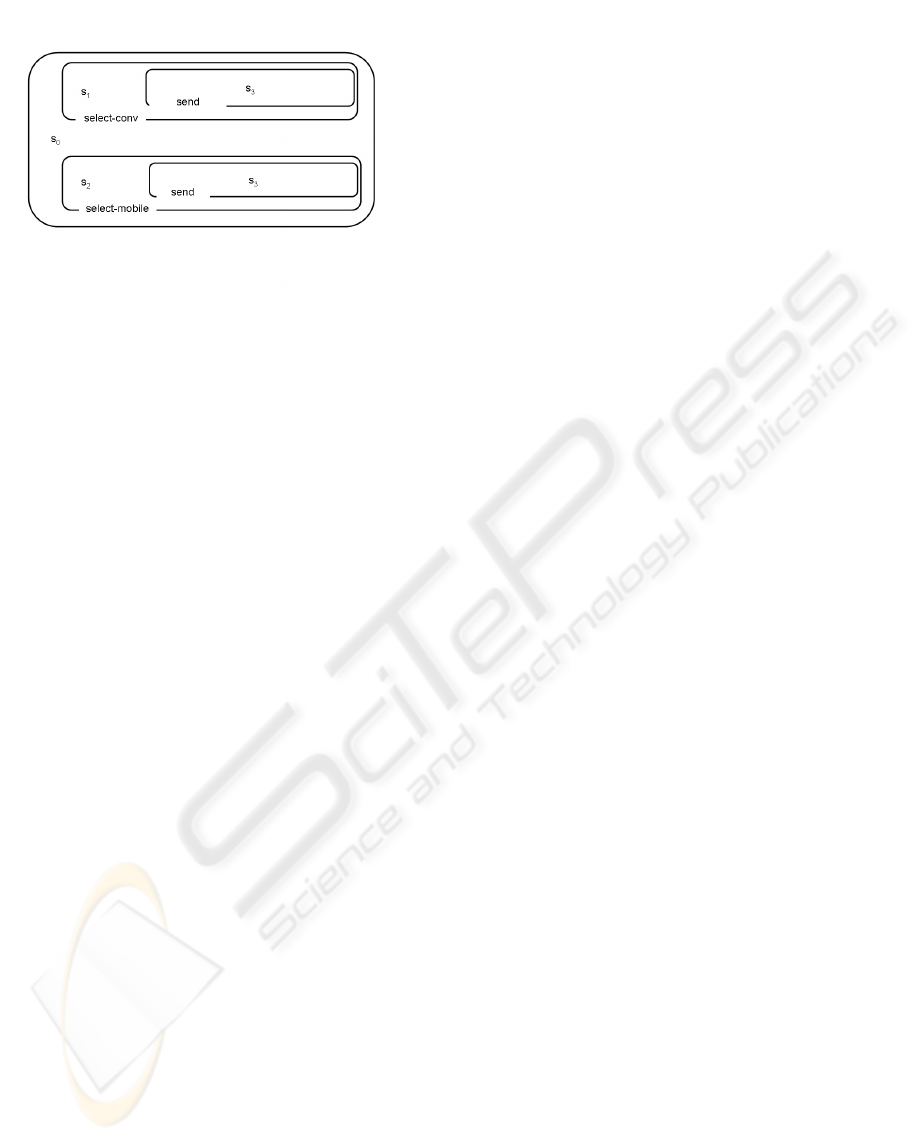
Figure 7: Behavior Represented by Nested Membranes.

we are not interested in retrieving the complete state

description or all capabilities of a given agent but ex-

clusively in the question if he is able to perform an

action which is described by a terminology. In order

to reason about problems of behavioral conformance

we introduce a tree-automaton which interprets be-

havioral descriptions as simulation experiments con-

cerning a certain agent (following (Vardi, 1998)). As

may be expected the functions know and next play a

prominent role in this experiments.

Since we rely on concepts from membrane comput-

ing again we ﬁrst show how to transform tree-like be-

havioral descriptions into membrane-based represen-

tations (cf. Figure 7). For simplicity we restrict our

attention to ﬁnite trees with a branching factor equal

or less than two. The concepts s

,...,s

which were

deﬁned in Figure 5 are now represented as molecules

ﬂoating in solutions contained in membranes. Succes-

sor states (of a given state) are represented by embed-

ded membranes which are labeled with a role name

representing the event whose occurrence is necessary

to access the state.

In order to support conformance testing it has to be

checked whether a given agent Ag supports a (possi-

bly incomplete) description of behavior. Intuitively in

our observation-based approach it is checked whether

the relevant concepts can be observed in the agent’s

current state and whether the concepts related to the

successor states can be observed in the the agent’s

successor states (which are accessed by the function

next). The relevant part of this line of reasoning can

be described by the following rule.

[know(Ag, A), [

[

]

] →

[know(next(Ag, b),B), [

[know(next(Ag, c),C), [

when know(Ag, A)=true

Due to space limitations we only consider a very

simple and general case. If the complex con-

cept A which has to be satisﬁed in the current

state of Ag holds in the current state (indicated by

know(Ag, A)=true) all embedded membranes

(representing the successor states) are investigated

concurrently. For this sake the automaton creates sev-

eral copies of itself (one for each successor state). For

the description of this self-reproductive behavior of

the automaton we exploit the feature of membrane di-

vision which is described by (P

aun, 2002). Note that

in this computational model large amounts of com-

putation space can be provided in linear time which

makes this type of computation surprisingly efﬁcient.

On the right-hand side of the rule each copy of the au-

tomaton works on a successor state of A (reached by

Ag’s transition function next together with role names

b resp. c) and a subtree of the original behavioral de-

scription. For the sake of our example concept names

A (resp. B and C) have to be bound to s

(resp. s

and s

) while the role names b and c have to be in-

stantiated with select-conv and select-mobile. In this

case a would represent the empty role .

5 DISTRIBUTED ACTION

As we already stressed we are interested in the sup-

port of reasoning about very abstract descriptions of

systems behavior. Such incomplete speciﬁcations

support a style of reasoning which exclusively consid-

ers relevant characteristics of behavior (and neglects

unimportant details). In this Section we give an ex-

ample for the treatment of incomplete speciﬁcations

of distributed actions.

Again we consider our example concerning the

choice of communication channels in a highly dy-

namic scenario (e.g. disaster management). Our dis-

cussion in this section is based on the intuition that

for our purposes it does not matter which agent de-

cides about the selection of the channel (i.e. the agent

himself or the environment). We are interested in sup-

porting a style of reasoning which is general enough

to support both scenarios from Subsection 2.1 (i.e.

which is general enough to recognize the naive sce-

nario and the presence of an intelligent environment).

In order to support this style of reasoning we sim-

ply extend our behavioral description from Section 4

with the following deﬁnitions. After this we extend

our automaton with the rules which are necessary to

process these constructs.

select-conv

= sel-conv-ag  sel-conv-env

select-mobile

= sel-mob-ag  sel-mob-env

send-msg

= snd-msg-ag  transfer-env

Note that in these terminological descriptions we

rely on complex roles for the description of complex

actions. In this case we again exploit the correspon-

dence between the description logics ALCFI

reg

and

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

104

converse-PDL. For example for an occurrence of an

event select-conv it sufﬁces that the event sel-conv-ag

or the event sel-conv-env occurs. For the occurrence

of event send-msg on the other hand we require the

events send-msg-ag and transfer-env to occur. These

constructs are processed by the following rules. Note

that we consider a complex agent C

= Ag, Env

in this example which consists from an elementary

agent Ag and the environment Env.

[know

,A), [

]

] →

[know

(next(C

),B), [

[know

(next(C

),B), [

when know

,A), b

= b

 b

[know

,A), [

]

] →

[know

(next(C

, [b

]),B),

[

]

when know

,A), b

= b

 b

Note that we treat a disjunction of subevents with

a rule which is similar to the rule in Section 4. Again

both branches of the disjunctions are processed con-

currently by individual automata. In the case of con-

junctions on the other hand we formulate our experi-

ment concerning the behavior of C

using a multi-

set of events [b

] such that no assumption is made

about the order of these events. Note that we use

a speciﬁc observation function for the compositional

agent C

. We use the function know

for the rep-

resentation of distributed knowledge (cf. (Fagin et al.,

1996)). Formally a proposition φ is distributed knowl-

edge among the agents A

if it is contained in the uni-

ﬁcation of all their individual knowledge. In the con-

text of our example the following holds:

know

,A) ⇔ know(Ag, A) ∨ know(Env,A).

6 COORDINATION

An essential problem in pervasive system consists in

the relation of individual agents and environment. Re-

lated questions are: how can an agent determine if his

actions make sense w.r.t. the behavior of the global

system? How can the consistency between individ-

ual information and the global state of knowledge be

ensured? From a systemic viewpoint this problem is

often called the scale gap (Krasnogor et al., 2005)

which may be observed between the behavior of the

individual and the strategy of the population. A typi-

cal scenario which illustrates the relevance of this is-

sue consists in a sudden and unexpected change of en-

vironmental conditions. Obviously it is necessary to

distribute information concerning the new state of af-

fairs as fast as possible. Especially it is not adequate

to distribute large quantities of information in such

situations. In fact it is prefered to distribute the mes-

sage that something happened as fast as possible. This

is necessary in order to prevent the agents from fol-

lowing strategies and routines which are inadequate

given the new environmental conditions.

We argue that the observation of social team perfor-

mance as well as the adoption of biological coordina-

tion mechanism can contribute to the solution of this

problem. As a starting point we take the observation

that in critical situations (which are frequently caused

by environmental changes) human agents do not re-

discuss all relevant topics. In fact they use they use in-

expensive communication mechanisms (e.g. nonver-

bal communication) in order to distribute the relevant

changes as fast as possible.

As a matter of fact such coordination mechanisms

have been observed in biology. Thus quorum sens-

ing is used by bacteria in order to coordinate individ-

ual behavior and the strategy of the population. In

our proposal we use the computational models which

were deﬁned for this coordination mechanism using

P-systems. Especially we apply simpliﬁed versions

of the concepts described in (Krasnogor et al., 2005).

We claim that the application of these models is help-

ful for the understanding of social coordination and

for the enhancement of coordination in pervasive set-

tings.

Basic Mechanisms. Since we are not able to de-

scribe the overall model (due to space limitations) we

have to content ourselves with the discussion of some

basic mechanisms. Biological coordination heavily

relies on the production and distribution of signal

molecules which are collected in the environment in

order to reﬂect the actual global state. Agents can re-

ceive such molecules and draw inferences about the

situation.

Example. We claim that in complex systems in-

formation about some facts is distributed all over the

system by mechanisms which are subtle but highly

efﬁcient. For the sake of modeling we reduce these

mechanisms to knowledge diffusion. We claim that

agents produce information which is ﬂoating in the

environment while executing cooperative tasks. For

example an agent which detects that the an environ-

mental conditions (e.g. the water level) deteriorates

distributes some information about this observation

while concurrently performing his tasks. We can

model this simple behavior by a rule which generates

information molecules.

[water-level-high] →

[(water-level-high, here), (serious-event, out)]

While the molecule water-level-high represents a

fuzzy assertion concerning the water level the mole-

cule serious-event is considered as a global stress in-

dicator. Note that this stress indicator is generated

KNOWLEDGE-BASED MODELING AND NATURAL COMPUTING FOR COORDINATION IN PERVASIVE

ENVIRONMENTS

105

repeatedly (as long as the water level is considered

as critical). Obviously the concentration of this type

of molecule in the environment is signiﬁcant. Since

the environment’s state is represented by a multiset

the concentration can be represented by the molecules

cardinality. The degree to which a certain an agent

is susceptible to systemic stress can be modeled by

a constant τ which deﬁnes a threshold for the stress

niveau.

[serious-event

] → [need-to-act], p >τ

When a certain concentration of stress is reached

agents are urged to act. This alertness is represented

my a molecule need-to-act which may operate as a

catalyzator for further actions. When the situation has

stabilized the stress indicator is metabolized by the

environment (e.g. using rules like serious-event →

Λ). Note that the molecule serious-event represent

only very general and vague information w.r.t. the

systems global state. This usage of vague information

is typical for robust coordination in critical situations.

7 CONCLUSIONS

In this paper we focused on the diffusion of knowl-

edge in complex system and pervasive settings as a

major factor shaping global behavior. We argued that

a sensitive handling of this ﬂoating of information en-

ables new possibilities concerning the understanding

and creation of novel kinds of behavior. We intro-

duced concepts from description logics for the rep-

resentation of knowledge and demonstrated the treat-

ment of highly abstract and incomplete behavioral de-

scriptions. For the formulation of the related algo-

rithms we introduced concepts from membrane com-

puting. Finally we argued that the transfer of sophisti-

cated interactions and coordination mechanisms from

ﬁelds like biology or sociology is possible on the ba-

sis of this paradigm. As direct beneﬁts of such an

approach we emphasize increased abilities to provide

meaningful behaviors in dynamic environments and

pervasive settings. Especially features like context-

awareness and autonomic behavior are supported by

this knowledge-based approach. Although we think

that the concepts from membrane computing are a

good foundation for modeling and simulation their

full computational power could solely exploited on

non-conventional hardware. We plan to extend our

research in this direction in the future.

We are indebted to the anonymous reviewers for

their lucid comments on an earlier versions of this pa-

per.

REFERENCES

Baader, F., Calvanese, D., McGuinness, D., Nardi, D., and

Patel-Schneider, P., editors (2003). The Description

Logic Handbook. Cambridge University Press, Cam-

bridge, U.K.

Berry, G. and Boudol, G. (1992). The chemical abstract

machine. Journal of Theoretical Computer Science,

96(1):217–248.

Fagin, R., Halpern, J. Y., Moses, Y., and Vardi, M. Y.

(1996). Reasoning about Knowledge. The MIT Press,

Cambridge, Mass.

Kephart, J. O. and Chess, D. M. (2003). The vision of auto-

nomic computing. IEEE Computer, 36(1):41–50.

Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic.

Theory and Applications. Prentice Hall, Upper Saddle

River, N.J.

Krasnogor, N., Georghe, M., Terrazas, G., Diggle, S.,

Williams, P., and Camara, M. (2005). An appealing

computational mechanism drawn from bacterial quo-

rum sensing. Bulletin of the European Association for

Theoretical Computer Science.

Leveson, N. (1995). Safeware. System safety and comput-

ers. Addison Wesley, Reading, Mass.

aun, G. (2000). Introduction to membrane computing.

Journal of Computer and System Science, 61(1):108–

143.

aun, G. (2002). Membrane Computing. An Introduction.

Springer, Berlin.

Pepper, P., Cebulla, M., Didrich, K., and Grieskamp, W.

(2002). From program languages to software lan-

guages. The Journal of Systems and Software, 60.

Perrow, C. (1984). Normal Accidents. Living with High-

Risk Technologies. Basic Books, New York.

Rutten, J. (1996). Universal coalgebra: a theory of systems.

Technical report, CWI, Amsterdam.

Schild, K. (1991). A correspondence theory for terminolog-

ical logics: Preliminary report. Technical Report KIT-

Report 91, Technische Universit

at Berlin, Franklinstr.

28/29, Berlin, Germany.

Straccia, U. (2001). Reasoning with fuzzy description logic.

Journal of Artiﬁcial Intelligence Research, 14:137–

166.

Vardi, M. Y. (1998). Reasoning about the past with two-

way automata. In Proc. of the 25th International Col-

loquium on Automata, Lanugages,and Programming.

Springer.

Wooldridge, M. J. (1992). The Logical Modelling of Com-

putational Multi-Agent Systems. PhD thesis, Depart-

ment of Computation. University of Manchester.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control,

8(3):338–353.

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

106