Ontology, Types and Semantics

Walid S. Saba

Department of Computer Science and Computer Engineering, American University of

Technology, Byblos, Lebanon P O Box 20

Abstract. In this paper we argue that many problems in the semantics of natu-

ral language are due to a large gap between semantics (which is an attempt at

understanding what we say in language about the world) and the way the world

is. This seemingly monumental effort can be grossly simplified if one assumes,

as Hobbs (1985) correctly observed some time ago, a theory of the world that

reflects the way we talk about it. We demonstrate here that assuming such a

strongly-typed ontology of commonsense knowledge reduces certain problems

to near triviality.

1 Introduction

In ‘Logic and Ontology’ Cocchiarella (2001) convincingly argues for a view of “logic

as a language" in contrast with the (now dominant) view of “logic as a calculus”. In

the latter, logic is viewed as an “abstract calculus that has no content of its own, and

which depends on set theory as a background framework by which such a calculus

might be syntactically described and semantically interpreted.” In the view of “logic

as a language”, however, logic has content, and “ontological content in particular.”

Moreover, and according to Cocchiarella, a logic with ontological content necessi-

tates the use of type theory (and predication), as opposed to set theory (and set mem-

bership), as the background framework. An obvious question that immediately comes

to mind here is: what exactly is the nature of this strongly-typed ontological structure

that will form the background framework for a new logic that has content?

In our opinion, part of the answer lies in an insightful observation that Hobbs

(1985) made some time ago, namely that difficulties encountered in the semantics of

natural language are due, in part, to difficulties encountered when one attempts to

specify the exact nature of the relationship between language and the world. While it

has not received much attention, the crucial point that Hobbs makes is the observation

that if one “assumes a theory of the world that is isomorphic to the way we talk about

it” (emphasis added), then “semantics becomes very nearly trivial”. Given the multi-

tude of difficult problems in the semantics of natural language (e.g., the semantics of

the so-called intensional verbs, the semantics of nominal compounds, and the difficult

problem of lexical ambiguity, to name just a few), a trivial semantics for natural lan-

guage might seem a far fetched goal. However, as will be demonstrated in this paper,

assuming a strongly-typed ontology that is isomorphic to the way we talk about the

world, does indeed make semantics very ‘nearly’ trivial.

S. Saba W. (2006).

Ontology, Types and Semantics.

In Proceedings of the 3rd International Workshop on Natural Language Understanding and Cognitive Science, pages 17-26

DOI: 10.5220/0002472300170026

 SciTePress

The picture we have in mind, depicted graphically as shown in figure 1 above, is a

logic and a semantics that is grounded in an ontological structure that reflects our

commonsense view of the world and the way we talk about it in our everyday lan-

guage. The structure of this strongly-typed ontology is in turn to be discovered, rather

than invented, using natural language itself, which is the best known theory of our

(shared) commonsense knowledge.

In this paper we first demonstrate that a number of problems in the semantics of

natural language can be reduced to near triviality, assuming a strongly-typed ontology

that reflects our commonsense knowledge exists. Subsequently, we briefly discuss the

nature of this ontological structure and how it may be discovered.

2 Nominal Compounds

The semantics of nominal compounds have received considerable attention by a

number of authors, most notably (Kamp & Partee, 1995; Fodor & Lepore, 1996;

Pustejovsky, 2001), and to our knowledge, the question of what is an appropriate

semantics for nominal compounds has not yet been settled. According to Weiskopf

(forthcoming), the problem of nominal compounds in the case of noun-noun combi-

nations is largely due to the multitude of possible relations that are usually implicit

between the two nouns. To illustrate, consider the following:



br ick house

{}

x x i s a that i s = house br ickmade of

(1)



dog house

{}

x x i s a that i s a = house dogmade for

(2)

Thus, while a brick house is a house ‘made of’ brick, a dog house is a house that is

‘made for’ a dog. It would seem, then, that the relation implicitly implied between the

two nouns differs with different noun-noun combinations. However, assuming the

existence of a strongly-typed ontology might result in identifying a handful of pat-

terns that can account for all noun-noun combinations.

As shown in the fragment hierarchy shown above, it would seem that madeOf is the

relation implicit between all

N N

[] combinations whenever N

is a Substance and

is a Artifact (throughout, we use this Font for concept types in the ontology, and

this font for predicate names. Thus, x::LivingThing means x is an object of type Liv-

ingThing and apple(x) means the predicate apple is true of x):





Substance Art ifact

{

PQ x Px::

λλ ∧Art ifact ( )

}

yQyxy(:: )( ,)∃∧Subst ance ( ) mad eO f ( )

(3)

The following are some example instances of (3), denoting the meanings of brick

house, wooden spoon, plastic knife and paper cup, respectively:





{

}

br i ck house x x E

:: ( )=∧Artifact h o use





{

}

wooden spoon x x E

:: ( )=∧Artifact spoon





{

}

plast i c kni fe x x E

:: ( )=∧Artifact k n if e



{

}

paper cup x x E

:: ( )=∧Artifact c up

where

Ey y xy

(:: )( () )≡∃ ∧Substance br ick madeOf ( , )

Ey y xy

(:: )( () )≡∃ ∧Subst ance w o o d mad eO f ( , )

Ey y xy

(:: )( () )≡∃ ∧Subst ance pl a st i c mad eO f ( , )

Ey y xy

(:: )( () )≡∃ ∧Substance paper madeOf ( , )

Note, however, that specific instances of Substance and specific instances of Artifact

might require the specialization of the relation suggested in (3). For example, con-

sider bread and knife, which are Substance and Artifact, respectively:

br ead : : FoodSubst ance Subst ance≺

(4)

knife :: Tool ... Instrument Artifact≺≺ ≺

(5)

While knife combines with a raw Substance (Material), such as plastic, bronze, wood,

paper, etc. with the relation madeOf, it combines with a FoodSubstance with the rela-

tion usedFor. Consider the following compounds of a FoodSubstance (which is a spe-

cific type of Substance) and some Instrument (a specific type of Artifact):





{

}

butter knife x x E

:: ( )=∧Instrument k nif e





{

}

coffee mug x x E

:: ( )=∧Inst rument mu g



{

}

cer eal box x x E

:: ( )=∧Instrument bo x

where

Ey y xy

(:: )( () )≡∃ ∧FoodSubst ance bu t t er u sed F o r ( , )

Ey y xy

(:: )( () )≡∃ ∧FoodSubst ance c o f f ee u sed F o r ( , )

Ey y xy

(:: )( () )≡∃ ∧FoodSubst ance c er ea l u sed F o r ( , )

Although we cannot dwell on such details here, we should point out that since the

purpose of an object of type Instrument (or more specifically, Tool) is to be used for

something, the specific type of usage would in turn be inferred from the specific In-

strument/Tool (e.g., cutting in the case of a knife, holding in the case of mug, etc.)

3 Intensionality and Compositionality

Like nominal compounds of the form

Noun Noun[]

the semantics of nominal com-

pounds of the form

dj Noun[]

have also traditionally been problematic, and, more

specifically, they have generally been considered as posing a serious challenge to the

general program of compositional semantics in the Montague (1974) tradition. Recall

that the simplest (extensional) semantic model for nominal constructions of the form

Adj Noun[]

is that of conjunction (or intersection) of predicates (or sets). For ex-

ample, assuming that red(x) and apple(x) represent the meanings of red and apple,

respectively, the meaning of a nominal such as red apple is given a



(

)

(

)

{

}

r ed apple x x x=∧red apple

(6)

What (6) says is that something is a red apple if it is red and apple. This simplistic

model, while seems adequate in this case (and indeed in many other instances of

similar ontological nature), clearly fails in the following cases, all of which involve

an adjective and a noun:

former senator

fake gun

alleged thief

(7)

(8)

(9)

Clearly, the simple conjunctive model, while seems to be adequate for situations

similar to those in (6), fails here, as it cannot be accepted that something is former

senator if it is former and senator, and similarly for the case of (8) and (9). In general,

therefore, more complex functions might be needed for other types of ontological

categories. In particular, what we seem to have is something like the following:





(

)

(

)

{

}

r ed apple x x x=∧r ed appl e





{| _ }for mer senat or x W asBut I sNot NowA x()= senat or



fake gun

{| _ }x LooksL i keBut I sNot A ct uallyA x()= gun





{| _ }alleged thief x I sNotButCouldPossiblyTurnOutT oBeA x()= thief

(10)

(11)

(12)

(13)

It would seem, then, that

different ontological categories require different compositional

functions

to compute the meaning of the whole from the meanings of the parts. In fact,

the meaning (intension) of some compound might not be captured without resorting

to temporal and/or modal operators. This has generally been taken as an argument

against compositionality, in that there does not seem to be an answer as to what the

compositional semantic function

F in













(

)

N N F N N

12 1 2

,= might be. We be-

lieve, however, that this is a fallacious argument in that the problem is not due to

compositionality but in ‘discovering’ a number of semantic functions that could ac-

count for all nominal compounds of different ontological categories. For example, we

argue that the following

are reasonable definitions for the concepts fake, former and al-

leged

Py Px Py xy

(:: )( ()

[( )( ( ) ( ) ( , ))])

∀

≡λ ∃ ¬ ∧ ∧

Physical

fake

l ooksLike::

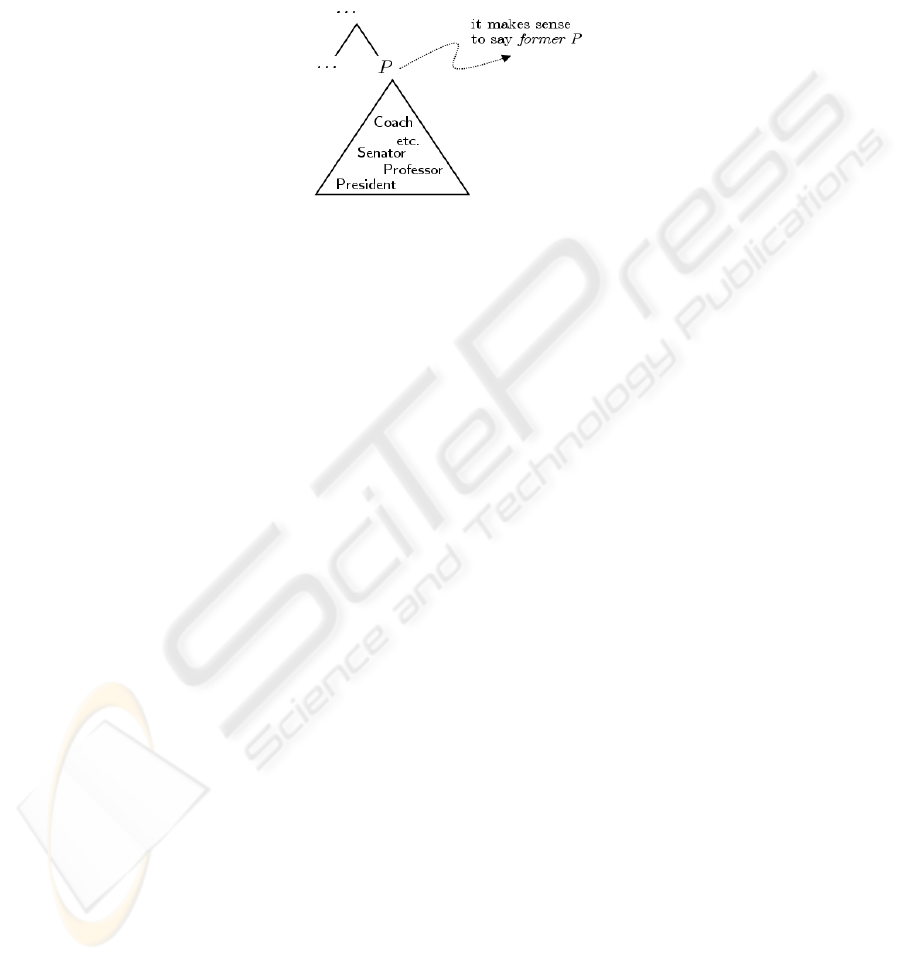
x x P t t now P x t P x now( :: )( [( )(( ) ( , ) ( , ))])∀≡λ∃<∧∧¬Rol e f o r me r ( )

x x P Pxnow t t now Pxt( :: )( [ ( , ) ( )(( ) ( , ))])∀≡λ¬∧∃∧◊Role alleged( )

(14)

(15)

(16)

That is, ‘fake’ applies to some concept

P as follows: a certain Physical object x is

a fake

P iff it is not a P, but it actually is similar (in certain respects) to some other

Physical object, say

y, which is actually a P. On the other hand, what (15) says is the

following: a certain

x is a former P iff x was a P at some point in time in the past and

is not now a

P. Finally, what (16) says is that something is an ‘alleged’ P iff it is not

now known to be a

P, but could possibly turn out to be a P in the future. It is interest-

ing to note here that the intension of

fake and that of former and alleged was in one

case represented by recourse to possible worlds semantics

– the case of (15) and (16),

while in (14) the intension uses something like structured semantics, assuming that

,xyl ooksLike( ) which is true of some x and some y if x and y share a number of

important features, is defined. What is interesting in this is that it suggests that possi-

ble-worlds semantics and structured semantics are not two distinct alternatives to

representing intensionality, as has been suggested in the literature, but that in fact

they should co-exist.

Some additional points should also be raised here. First, the representation of the

meaning of

fake given in (14) suggests that fake expects a concept which is of type

Artifact, and thus something like fake idea, or fake song, for example, should sound

meaningless, from the standpoint of commonsense (One can of course say

fake smile,

but this is clearly another sense of

fake. While fake gun refers to a gun (which is an

Artifact) that is not real, fake smile refers to a dishonest smile, or a smile that is not genu-

ine). Second, we should note that the representation of the meaning of

former given

in (15) suggests that

former expects a concept which has a time dimension, i.e. is a

temporal concept. Finally, we should note here that our ultimate goal of this type of

analysis is to discover the various ontological categories that share the same behav-

iour. For example, conjunction, which as discussed above is one possible function

that can be used to attain a compositional meaning, seems to be adequate for all

nominal constructions of the form [

A N] where A is a physical property (such as red,

large, heavy

, etc.) and N is a physical object (such as car, person, desk, etc.), as ex-

pressed in (17), which states that some adjectives are intersective, although it says

nothing about the meaning of such adjectives:



A N =

|{}xA x N x() ()∧

PhysicalProperty PhysicalThing

(17)

Similarly, an analysis of the meaning of

former, given in (16), suggests that there

are a number of ontological categories that seem to have the same behaviour, and

could thus replace

P in (15), as implied by the fragment hierarchy shown below.

4 On Intensional Verbs

The argument we have been making thus far can be summarized as follows: assuming

the existence of

a strongly-typed ontology that reflects our commonsense view of the world

and the way we talk about it

, can help resolve a number of problems in the semantics of

natural language. In this section we tackle the semantics of the so-called intensional

verbs. Let us look at the following examples, which (Montague, 1969) discussed in

addressing a puzzle pointed out to him by Quine:



John pai nted a elephant

(

)

(

)

(

)

(

)

xxjx,=∃ ∧el ephant paint ed





John found a elephant

(

)

(

)

(

)

(

)

xxjx,=∃ ∧el ephant f ound

(18)

(19)

The puzzle Quine was referring to here was the following: both translations ad-

mit the inference

(∃x)(elephant(x)) – that is, both sentences imply the existence of an

elephant, although it is quite clear that such an inference should not be admitted in the

case of (19). According to Montague, the obvious difference between (18) and (19)

must be reflected in an ontological difference between find and paint in that the ex-

tensional type

))((tee →→

both transitive verbs are typically assigned is too

simplistic. While Montague’s solution to this problem was to suggest that some tran-

sitive verbs are intensional, we argue that the problem lies in the flat type structure

assumed in Montague’s intensional logic. That is, we argue that a more complex type

system is needed, one that would in fact yield different types for find and paint. One

reasonable suggestion for

find and paint, for example, could be as follows:

find e e t:: ( ( ))→→

Animal Thing

pai nt e e t:: ( ( ))→→

Human Representation

(20)

(21)

Thus, instead of the flat type structure implied by

))((tee →→

, the types of find

and paint should reflect our commonsense belief that we can always speak of some

Animal that found something (i.e., any Thing whatsoever), and of a

Human that

painted some illustration, or as we called it here a

Representation. With this back-

ground, the proper translation of (18) and (19) and the corresponding inferences can

now be given as follows:





John pai nted a elephant

xx(:: )( ()

∃ Representation el ephant

jx(:: ,))

∧

Humanpaint ed





John found a elephant x x(:: )( ()

∃ Thing el ephant

(22)

(23)

So what do we have now? (23) clearly implies

xx()( ())

∃

Thing:: el ephant

That is, (23) implies there is some object

x of type Thing, of which the predicate ele-

phant

is true. Note, also, that

xx() ( :: )

⊃

Elephantel ephant

, i.e., if

x()el ephant is true of some object x, then x must be object of type Elephant. There-

fore, the expression

xx()( ())∃ Thing:: el ephant

can be thought of as being is an

abbreviation of

xx()( (::))∃ Thing Elephant:: el ephant

. That is, we have an ex-

pression that refers to an object

x which is both, an Elephant and a Thing, which is fine,

since

... ...Elephant Animal T hing≺≺ ≺≺

as the fragment hierarchy shown below

implies. In these cases we say that the two types unify.

However

xx()(())∃ Repr esent at i on:: el ephant

, which is what is implied by (22),

is an abbreviation of the expression

xx()((::))

∃

Represent at ion Elephantel ephant::

(24)

In (24) we are now referring to an object

x which is of type Elephant and of type

Representation. As shown in the fragment hierarchy of the figure shown above, these

two types do not unify (neither is a subtype of the other). Instead of the subtype rela-

tion that exists between

Elephant and Thing, another association must be inferred

between

Elephant and Representation. As shown in figure 4, an object of type Represen-

tation

is a representation of something, and presumably, any Thing whatsoever (much

like an object of type

Story is a story about some Thing!) The conclusion of this discus-

sion is that (22) and (23) given above result in the inferences given in (25) and (26),

respectively:

xx()(())∃ Repr esent at i on:: el ephant

xx()( ())∃ Thing:: el ephant

(25)

(26)

Eureka! Adding a rich type structure to the semantics seems to have solved Quine

’s

puzzle, as the correct inferences can now be made: if John

found an elephant, then one

could indeed infer that an actual elephant exists. However, the

painting of an elephant

only implies the existence of a representation (an illustration) of something we call an

elephant! Stated yet in other words, (23) implies an elephant

Thing exists, while (22)

simply implies the existence of an elephant

Representation.

5 Language, Logic and Ontology

In this paper we have been making the following argument: semantics can be made

‘nearly’ trivial, as Hobbs (1985) correctly observed, if the semantics is grounded in

strongly-typed ontological structure. The goal we have in mind is a formal system,

much like arithmetic (or any other algebra) for concepts, as has been advocated by a

number of authors, such as Cresswell (1973) and Barwise (1989), among others.

What we are arguing for is a formal system that explains how concepts of various

types combine, forming more complex concepts. To illustrate, consider the following:

ar t i fi ci al →NaturalKind Artifact::

(27)

<< <flower ... ...Plant LivingThing NaturalKind::

(28)

What the above says is the following:

artificial is a function that takes a Natu-

ralKind and returns an Artifact (27); a

flower is a Plant which is a LivingThing which

in turn is a NaturalKind (28). Therefore, ‘artificial c’, for some NaturalKind c, should

in the final analysis have the same properties that any other Artifact has. Thus, while

flower, which is of type Plant, grows, lives and dies like any other LivingThing, an

artificial flower, and like any other Artifact, is not something that grows, lives and

dies, etc., but is something that is manufactured, can be assembled, destroyed, etc.

The concept algebra we have in mind should also systematically explain the in-

terplay between what is considered commonsense at the linguistic level, type check-

ing at the ontological level, and deduction at the logical level. For example, the con-

cept

artificial car, which is a meaningless concept from the standpoint of commonsense,

is ill-typed since

Car is an Artifact, and Artifact does not unify with NaturalKind – neither

type is a sub-type of the other. The concept

former father, on the other hand, which is

also a meaningless concept from the standpoint of commonsense, escapes type-

checking since

father, which is a Role, is a type that former expects (recall the meaning

former given in (15) above). However, given the meaning of former, and an expres-

sion stating that 'once someone is a father he is always a father

’, expressed as

xt xt( )(( )( ,∀∃father( )

ttt xt( )(( ) , )))⊃∀ > ⊃

22 2

father( )

one can easily show that

the concept

former father, while it escapes type-checking, eventually results in logical

contradiction at the logical level. A proper formulation of the nature of interplay

between language, ontology and logic, and correspondingly between commonsense,

strong typing and deduction (as illustrated in figure 1 above), is what we believe is

needed to ultimately have a

‘trivial semantics’ for natural language. Clearly, the most

challenging task in this endeavour is nature of this ontological structure that reflects

our commonsense view of the world and the way we talk about it (the middle layer in

figure 1). But what is the nature of this ontological structure? First, since concepts we

talk about in our ordinary language are public, then the structure of commonsense

ontology must be shared, and subsequently this structure must be ‘discovered’ rather

than ‘invented’. Second, natural language, which is the best known theory of com-

monsense, should itself be used as guide to discovering this structure. As we demon-

strated above, an analysis of nominal compounds and so-called intensional verbs can

give us important insights into the nature of this ontological structure that underlies

natural language.

In addition to the analysis of nominal compounds and intensional verbs, an

analysis of verbs and adjectives that may or may not plausibly apply to nouns can

also help us discover another piece of the puzzle. This process is very much similar to

the process of type inferencing in higher-order, pure, polymorphic functional lan-

guages. First, we start this discussion by introducing a predicate

app(p,c) which is

taken to be true of a property

p and a concept c iff ‘it makes sense to speak of the prop-

erty

p of c’. Consider now the following two sets

{

}

P,= largesmart

and

{

}

C,= Table Elephant

. A quick analysis of app(p,c) on the four adjective-noun com-

binations yields

app(large,Table), app(large,Elephant), app(smart,Elephant),

¬app(smart,Table). That is, while it makes sense to say ‘large table’, ‘large elephant’,

and

‘smart elephant’, it does not make sense to say ‘smart table’. This kind of analysis

yields the following structure:

Note that this structure was discovered and not invented. Note also that the deci-

sions that lead to this structure, namely the application of the predicate

app(p,c) on the

four adjective-noun combinations could not be questioned. Moreover, the answer to

these queries must be Boolean-valued

– that is, while it could be a matter of degree as

to how smart a

certain elephant might be (which is a quantitative question), the qualita-

tive

question of whether or not it is meaningful to say `smart elephant’ is not a matter

of degree. This has subsequently meant that the type-hierarchy we seek might be a

strict binary tree with no multiple inheritance. For lack of space we cannot discuss

this issue in more depth here. Instead, we refer the reader to (Saba, 2006) for more

details on how such a ontology of commonsense knowledge might be discovered

(rather than invented), using natural language itself as a guide in this process.

6 Concluding Remarks

In this paper we have argued that many problems in the semantics of natural language

are due to a large gap between semantics (which is an attempt at understanding what

we say in language about the world) and the way the world is. This seemingly monu-

mental effort can be grossly simplified if one assumes, as Hobbs (1985) observed

some time ago, a theory of the world that reflects the way we talk about it.

We have shown here that assuming such a theory (i.e., such a strongly-typed on-

tology of commonsense concepts) reduces certain problems to near triviality. Discov-

ering such an ontological structure is clearly another matter. Clearly, however, since

natural language is the best known theory of our (shared) commonsense knowledge,

analyzing natural language and the way we talk about the world is the best avenue to

discovering the nature of this ontological structure. Finally, and not withstanding

some novel efforts to build such knowledge structures (such as Lenat & Ghua, 1990;

Mahesh & Nirenburg, 1995; Sowa, 1995), we believe that the ontological structure

that reflects our commonsense view of the world is shared, and thus attempts at in-

venting (rather than discovering) this structure have minimal chances of success.

References

1. Barwise, J. (1989), The Situation in Logic, CSLI Publications, Stanford.

2. Cochiarella, N. B. (2001), Logic and Ontology, Axiomathes, 12, pp. 117-150.

3. Cresswell, M. J. (1973), Logics and Languages, Methuen & Co., London.

4. Fodor, J. & Lepore, E. (1996), The pet fish and the red herring: why concepts aren't

prototypes, Cognition 58, pp. 243–276

5. Hobbs, J. (1985), Ontological Promiscuity, In Proc. of ACL-85, pp. 61--69, Chicago, Illi-

nois, 1985. ACL.

6. Kamp, H. & B. Partee. 1995. Prototype theory and Compositionality, Cognition, 57, pp.

129-191.

7. Lenat, D. B. and Guha, R.V. (1990), Building Large Knowledge-Based Systems: Represen-

tation & Inference in the CYC Project. Addison-Wesley.

8. Mahesh, K. and Nirenburg, S. (1995), A Situated Ontology for Practical NLP, In IJCAI-95

Workshop on Basic Ontological Issues in Knowledge Sharing, August 1995, Montreal,

Canada. Montague, R. (1960), On the Nature of Certain Philosophical Entities, The Monist,

53, pp. 159-194

9. Montague, R. (1974), In Formal Philosophy: Selected Papers of Richard Montague, R.

Thomasson (Ed.), Yale University Press.

10. Pustejovsky, J. (2001), Type Construction and the Logic of Concepts, In P. Bouillon and F.

Busa (Eds.), The Syntax of Word Meanings, Cambridge University Press.

11. Saba, W. S. (2006), Language, Logic & Ontology – Uncovering the Structure of Common-

sense Knowledge, accepted in International Journal of Human-Computer Studies – IJHCS

(to appear).

12. Sowa, J. F. (1995). Knowledge Representation: Logical, Philosophical, and Computational

Foundations. Boston, MA: PWS Publishing.

13. Weiskopf, D. A. (forthcoming), Compound Nominals, Context & Compositionality, Syn-

these, to appear.