
Honeynets in 3G – A Game Theoretic Analysis
Christos K. Dimitriadis
University of Piraeus, 80 A. Dimitriou, 18534 Piraeus, Greece
Abstract. Although security improvements were implemented in the air
interface of Third Generation (3G) mobile systems, important security
vulnerabilities remain in the mobile core network, threatening the whole service
provision path. This paper presents an overview of the results of a security
assessment on the Packet Switched domain of a mobile operator’s core network
and studies the benefits from implementing a Honeynet in 3G, by the
deployment of game theory.
1 Introduction
The improvement of 3G security mainly focuses on the air-interface, by implementing
mobile terminal to UMTS Terrestrial Radio Access Network (UTRAN) mutual
authentication, as well as solving a number of existing problems caused by
vulnerabilities of the underlying cryptographic technology of 2G [1]. Having these
features in mind, 3G mobile subscribers may feel more secure when connecting in 3G
networks. This sense of security however, could be proven of being more a perception
than a strict reflection of reality, if except from the UTRAN, we consider all elements
in the service provision path, including the mobile core network.
The 3G core network consists of the Circuit Switched (CS) domain, the Packet
Switched (PS) domain and the IP Multimedia Subsystem (IMS) [2]. The CS domain
serves traffic switching and signaling for voice mobile connections, linking the
UTRAN with other voice networks such as the Public Switched Telephone Network
(PSTN). The PS domain, serves traffic switching and signaling for data connections,
linking the UTRAN with other Packet Domain Networks (PDNs), including the
Internet. The IMS is a complementary subsystem, providing multimedia services over
the PS domain.
This paper identifies open security issues of the PS domain of 3G core networks.
The problem is defined by presenting vulnerabilities and threats identified through a
practical security assessment, which was enriched and validated by a desk research
study on core network security. The introduction of Honeynet technologies is studied,
as a cost effective solution that increases security and provides valuable knowledge to
the security engineers of the mobile operator, towards the addressing of the identified
security issues.
The paper is organized in two main sections, not including the introduction and
conclusions. Section 2, presents an overview of the results of a security assessment
that was conducted on the PS domain of a major mobile operator. This section is
K. Dimitriadis C. (2006).
Honeynets in 3G – A Game Theoretic Analysis.
In Proceedings of the 4th International Workshop on Security in Information Systems, pages 146-152
Copyright
c
SciTePress

enriched with key vulnerabilities of the PS architecture of mobile operators at a global
level, as reported in research papers. In Section 3, Game Theory is deployed in order
to formally present the security advantages from implementing a Honeynet in 3G, as a
response to the identified security issues.
2 3G core Network Security Assessment
During the recent years, mobile telecommunication networks were transformed from
infrastructures that provided voice and very limited data services to infrastructures
that provide a wide range of multimedia data services [3]. The outcome of this
transformation was far different from a mobile core network built from the beginning
according to an organized design based on the new requirements and specifications. It
was an upgrade of the existing closed Signalling System 7 (SS7) based networks to
Internet Protocol (IP) based systems that combined a number of old and new
technologies and applications under the pressure of timely service delivery start-up.
This situation created a number of security vulnerabilities, reported by several
studies in the field, including flat mobile core networks and management networks,
shared operations and management networks also connecting to corporate networks,
insecure billing an lawful interception connectivity, huge number of device logs, not
correlated and not manageable, lack of adequate security capabilities of legacy
systems and inadequate filtering on border gateways [4, 5 , 6, 7, 8].
A security assessment of the PS domain of a major mobile operator validated the
existence of these vulnerabilities and revealed some new ones. An overview of the
main groups of vulnerabilities discovered are presented below:
• Uncontrolled communication with roaming partners
• Insufficient or non-existent logging facilities
• Absence of programmed log inspection processes
• Lack of network intrusion detection or prevention systems
• Inadequate firewall architectures
• Inexistence of security layers depending on the security needs of each part of the
PS core network
Additionally, we discovered a number of non-network security related
vulnerabilities, such as inadequate access control mechanisms for all elements of the
PS core network and direct access of business users to critical systems, without an
adequate business need for justifying the risk.
These vulnerabilities lead to threats, including:
• Critical production systems, such as the Gateway GPRS
1
Support Nodes (GGSNs)
and Serving GPRS Support Nodes (SGSNs), exposed to attacks.
• Exposed GPRS gateways (SGSN and GGSN) may become vaulting houses for
attacking critical systems that are uncontrollably connected to them, such as the
Home Location Register (HLR), the Mobile Switching Center (MSC), the charging
gateways or the billing gateways. This threat reveals an incompetence of protecting
critical systems from attacks launched from the inside of the mobile operator.
1
General Packet Radio Service
147

• The core network of the mobile operator becomes a logical extension of the core
network of the roaming partner with limited control, exposing both to serious
threats, impacting security from and to external (roaming partners) nodes.
• The insufficient logging facility in combination with the non-existent intrusion
detection systems impacts the timely identification of an intrusion, as well as
forensics.
The above threats can be summarized as loss of confidentiality, integrity and
availability of critical data, including legal-sensitive subscriber personal data and call
details, as well as critical systems. All these vulnerabilities in correlation with the
increased business impact from the realization of a threat, reveal a lack of awareness
and knowledge of security issues regarding the PS domain of the mobile core
network.
3 Analysis through Game Theory
A Honeynet, is an architecture of information systems, whose value lies in
unauthorized or illicit use of that resource, in order to be able to learn from attacking
entities and improve the existing security architectures and systems [9]. Honeynets
include a gateway called honeywall, which controls and captures network packets, in
order not only to study them by also to protect other information systems from attacks
launched from the compromised systems of the Honeynet.
We assume a Honeynet architecture, called PSH_NET, operating in a 3G
infrastructure. PSH_NET, is preventive, since it can be used as a decoy, being an easy
target for attackers who are being distracted from the production systems of the
mobile operator. PSH_NET is also detective, since potential attacks to real systems
are detected and analyzed. PSH_NET is finally reactive, since the detection of an
attack warns the security engineers of the mobile operator and the knowledge gained
from the analysis of the attacks helps them improve the existing security architecture
of the mobile core network.
In order to study the benefits of deploying PSH_NET, we deploy Game Theory, as
a mean of formalizing the expressions of our rational. Game Theory is a set of applied
mathematical models which aim to study cooperative and confict interactions with
formalised incentive structures [10]. The foundations of Game Theory lie on the
publication of Augustin Cournot “Researches into the Mathematical Principles of the
Theory of Wealth”. Game theory was founded as a scientific field by John von
Neumann in 1944 by the publication of “The Theory of Games and Economic
Behavior”, which he wrote in collaboration with Oskar Morgenstern. John Nash
introduced in 1950 a principle called Nash equilibrium, proving that the best
responses of all players are in accordance with each other [11].
Our target is the comparison of a mobile operator that implements a Honeynet,
with a mobile operator that doesn’t and study different situations as far as security is
concerned. For this purpose, we define a game called PSH_NET-G. This game is non-
cooperative, since the mobile operators do not have a common security infrastructure
and static since players may make simultaneous moves. Furthermore, PSH_NET-G is
a non-zero sum game, meaning that the total benefit of all players in the game is not
148

zero, because there is no relationship between the gain of one player and the loss of
the other.
PSH_NET-G is a structure of a set of players (N), a set of strategies Σ and a set of
payoffs P, defined by the following expression:
∏
∈
→Σ
Ni
P
ι
π
:
(1)
where N={1,2}, Σ
ι
is the strategy space of player i and
N
RP →
is the players’
payoff at the end of the game.
We define two players, the Mobile Operator 1 (MO1), who is a mobile operator
that implements a Honeynet architecture, and Mobile Operator 2 (MO2), who is a
mobile operator who doesn’t. For each player there are two possible strategies, or
more precisely for our study, modes of behavior, depending on whether the player’s
nodes are compromised by the realization of a security incident, or not compromised:
• Σ1: compromised node behavior
• Σ2: normal node behavior
Forward to the above, Σ
ι
=(Σ1, Σ2). By following this logic, instead of traditionally
studying the gain of the possible moves of the players, we are studying the gain of
implementing or not a Honeynet in different security related situations.
The payoff receives specific values from a definite set P={P1, P2,…, Pm}. Let
each possible payoff Pi, where i={1,2,…,m}, be a sum of gains from Table 1,
depending on a specific condition.
Table 1. Gain types and values.
Gain ID Description Gain value
G
1
Self-security from internal nodes 10
G
2
Security from external nodes 10
G
3
Security to external nodes 10
G
4
Knowledge 10
G
5
Cost -5
The first three gains correspond to the threats described in the previous section,
including attacks from the inside, as well as attacks to and from external nodes
(especially roaming partners). The fourth gain corresponds to the knowledge
produced by a security architecture that is able to study attacks and evolve according
to the tactics of the attackers. The last gain is a negative one, corresponding to the
cost of an additional open source security architecture.
Forward to the above, Pi is defined by the following equation: Pi=a
1
G
1
+a
2
G
2
+
a
3
G
3
+ a
4
G
4
+ a
5
G
5
. The parameters a
n
={0,1} (n={1,2,3,4,5}), are 1 when the player
receives the corresponding gain in a specific condition and 0 in the opposite scenario.
The payoff matrix of a game shows what payoff each player will receive, as an
outcome of the game, depending on the combined actions of the players. The payoff
matrix of PSH_NET-G is presented in Table 2.
149

Table 2. Payoff matrix of PSH_NET-G.
MO2
Attack Normal
Attack 35,10 25,10
MO1
Normal 15,10 -5,0
In more detail, when both operators have compromised nodes, we have an Attack-
Attack condition, where MO1 receives all gains of Table 1, protecting its internal
nodes, preventing attacks to other mobile operators, gaining knowledge and also
paying the Honeynet cost. MO2, who does not implement the honeynet, receives only
gain G2, while being protected from the compromised node of MO1 (blocked by the
Honeynet), revealing a network gain for all players. In an Attack-Normal condition,
MO1, does not receive the G2 gain since MO2 is not attacking, but receives the rest
of the gains as in the previous condition. MO2, receives gain G2, like in the previous
condition. In a Normal-Attack condition, MO1 receives gains G2,G4 and G5, while
MO2 receives gain G3, since MO1 is protected by the Honeynet. In a Normal-Normal
condition there is no positive gain for the players, while MO1 pays the cost of the
Honeynet.
The payoff matrix reveals two Nash Equilibria. A Nash equilibrium is identified,
by marking the best responses of a player, taking as constant the response the other
player. For example if MO2 lies in an attack mode, the attack mode of MO1 is the one
with the greatest payoff for MO1. By marking in bold these payoffs, we identify two
Nash equilibria, Attack-Attack and Attack-Normal, which are the conditions that lead
both players to a mutual best advantage.
Analyzing the results of the game we conclude to the following:
• There is a net benefit for all players due to the implementation of the Honeynet,
shown in the Attack-Attack situation, since security depends on the security of
others. This net benefit could be increased by the proliferation of knowledge
gained by MO1.
• There are two Nash equilibria, Attack-Attack and Attack-Normal, revealing that
the implementation of a Honeynet is most useful for both players in these
situations.
• In the case that MO2 is compromised and forced to attack, there is a clear benefit
for the MO1, who implements the Honeynet.
• The highest payoffs are received by MO1, who implements the Honeynet, except
from the case that there is no security incident.
The possibilities, however, for the realization of no security incident are proven to
be very small, which when combined with the low cost of implementing open source
solutions, like Honeynets, reveal the cost effectiveness of Honeynets in 3G. In order
to prove more formally this expression, we use a concept of economics and finance
theory, called risk aversion [12]. An entity is risk averse, when it is willing to accept a
lower expected payoff if it means that it could have a more predictable outcome.
Mobile operators are a very good example of risk averse entities, in contradiction to
risk seeking entities, due to the increased business impact from the realization of a
threat in the PS, especially when the cost of a security solution is very low.
The following equation, represents the gain in security, as a function of the
monetary value that the entity is willing to invest in security: y=f(x). The f function is
150
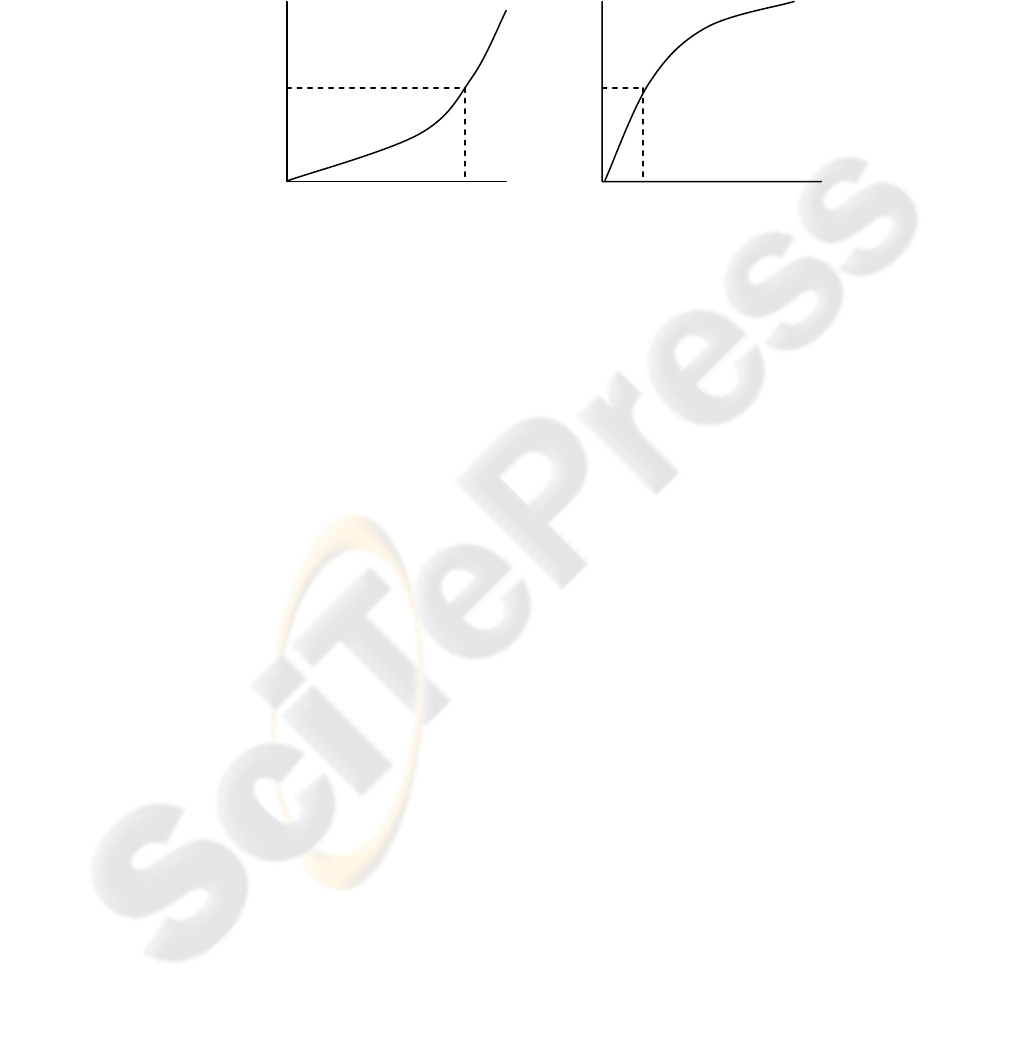
convex, if the entity is risk averse, meaning that this entity is willing to invest more
money in order to have a more predictable result, and concave if the entity is risk
seeking, meaning that this entity is not willing to invest money in security and take
chances. The corresponding curves, which we should mention that they are inverted
in gambling situations, are shown in Fig. 1.
Fig. 1. Risk averse and risk seeking behavior.
The dotted lines in Fig. 1, represent another concept called certainty equivalents,
meaning that if there is a 50% possibility for a security incident to occur, the first
entity would invest more money in order to ensure that it will be addressed by
countermeasures, while the second one would take more chances, building a less
expensive architecture. However, in the case of honeynets, y>>x, meaning that the
cost of an open source solution like a Honeynet is much smaller than the cost from a
security incident in a production system on a 3G architecture, where most applications
are time sensitive. Taking into account the results of PSH_NET-G and the results of
the risk-aversion study, we conclude that Honeynets are a cost-effective security
solution with important security benefits.
4 Conclusions and Future Work
Although the latest 3G standards and implementations improved UTRAN security,
important security issues remain in the mobile core network, threatening the whole
security chain. This paper presented a summary of the results of a security assessment
on the PS domain of a mobile operator’s core network and deployed game theory, in
order to study the benefits from implementing a Honeynet architecture in 3G.
The results of the game theoretic analysis in combination with the deployment of
risk-aversion theory concluded that PSH_NET is a cost-effective security solution
that provides important security benefits to mobile operators. PSH_NET is primarily
dealing with the lack of knowledge and awareness regarding specialized attacks
against the 3G core network, which leads to inadequate firewall and network intrusion
detection-prevention architectures, as well as to uncontrolled communication with
roaming partners.
x = monetary
y (utility =
security)
y (utility =
security)
x = monetary cost
151

Future work regards the implementation and practical testing of PSH_NET in order
to prove its advantages and contribution in practice.
References
1. Neimi, V., Nyberg, K.: UMTS Security. John Wiley & Sons (2003)
2. 3rd Generation Partnership Project: TS 23.002 - Network architecture (2004)
3. Wisely, D., Eardley, P., Burness, L.: IP for 3G—Networking Technologies for Mobile
Communications. John Wiley & Sons, ISBN 0-471-48697-3 (2002)
4. Whitehouse, O., Murphy, G.:Attacks and Counter Measures in 2.5G and 3G Cellular IP
Networks. @stake press (2004)
5. Kameswari, K., Peng, L., Yan. S., Thomas, F.,L,: A Taxonomy of Cyber Attacks on 3G
Networks. IEEE International Conference on Intelligence and Security (2005).
6. Donald, W., Scott, L.: Wireless Security Threat Taxonomy, IEEE Workshop on
Information Assurance (2003)
7. El-Fishway, N., Nofal, M., Tadros, A.: An Improvement on Secure Communication in PCS.
Performance, Computing, and Communications Conference, Conference Proceedings of the
2003 IEEE International (2003)
8. Mitchell, C. J.: Security for Mobility. IEE Telecommunication Series, 51, 2004.
9. The Honeynet Project Know Your Enemy. 2nd ed Learning About Security Threats.
Addison-Wesley (2004)
10. Osborne, M.J., Rubinstein, A.: A course in game theory, MIT press (1997)
11. Nash, J.: Equilibrium points in n-person games. Proceedings of the National Academy of
the USA 36(1):48-49 (1950)
12. Rabin, M.: Risk Aversion and Expected-Utility Theory: A Calibration Theorem,
Econometrica 68(5), 1281-1292, September (2000)
152
