Large Scale Face Recognition with Kernel Correlation

Feature Analysis with Support Vector Machines

Jingu Heo, Marios Savvides and B. V. K. Vijayakumar

Department of Electrical and Computer Engineering

Carnegie Mellon University, U.S.A

Abstract. Recently, Direct Linear Discriminant Analysis (LDA) and Gram-

Schmidt LDA methods have been proposed for face recognition. By utilizing the

smallest eigenvalues in the within-class scatter matrix they exhibit better

performance compared to Eigenfaces and Fisherfaces. However, these linear

subspace methods may not discriminate faces well due to large nonlinear

distortions in the face images. Redundant class dependence feature analysis

(CFA) method exhibits superior performance compared to other methods by

representing nonlinear features well. We show that with a proper choice of

nonlinear features in the CFA, the performance is significantly improved.

Evaluation is performed with PCA, KPCA, KDA, and KCFA using different

distance measures on a large scale database from the Face Recognition Grand

Challenge (FRGC). By incorporating the SVM for a new distance measure, the

performance gain is significant regardless of which algorithm is used for feature

extraction, with our proposed KCFA+SVM performing the best at 85% at 0.1%

FAR where the baseline PCA gives only 12% at 0.1% FAR.

1 Introduction

Machine recognition of human faces from still and video images is an active research

area due to the increasing demand for authentication in commercial and law

enforcement applications. Despite some practical successes, face recognition is still a

highly challenging task due to large nonlinear distortions caused by normalization

errors, expressions, poses and illumination changes. Two well-known algorithms for

face recognition are Eigenfaces 1 and Fisherfaces 2. The Eigenfaces method

generates features that capture the holistic nature of faces through the Principal

Component Analysis (PCA), which determines a lower-dimensional subspace that

offers minimum mean squared error approximation to the original high-dimensional

data. Instead of seeking a subspace that is efficient for representation, the Linear

Discriminant Analysis (LDA) method seeks directions that are efficient for

discrimination. Due to the fact that the number of training images is smaller than the

number of pixels, the within-class scatter matrix S

is singular causing problems for

LDA. The Fisherfaces performs PCA to overcome this singular-matrix problem and

applies LDA in the lower-dimensional subspace. Recently, it has been suggested that

the null space of the S

is important for discrimination. The claim is that applying

PCA in Fisherfaces may discard discriminative information since the null space of the

contains the most discriminative power. Fueled by this finding, Direct LDA

Heo J., Savvides M. and V. K. Vijayakumar B. (2006).

Large Scale Face Recognition with Kernel Correlation Feature Analysis with Support Vector Machines.

In 6th International Workshop on Pattern Recognition in Information Systems, pages 15-24

DOI: 10.5220/0002487300150024

 SciTePress

(DLDA) 3 and Gram-Schmidt LDA (GSLDA) 4 methods have been proposed by

utilizing the smallest eigenvalues in the S

. However, these linear subspace methods

may not discriminate faces well due to large nonlinear distortions in the faces. In such

cases, correlation filter approach may be attractive because of its ability to tolerate

some level of distortions 5.

One of recent techniques in correlation filters is redundant class dependence feature

analysis (CFA) 6 which exhibits superior performance compared to other methods.

We will show that with a proper choice of nonlinear features, the performance can be

dramatically improved. Our evaluation includes CFA, GSLDA, and Eigenfaces on a

large scale database from the face recognition grand challenge (FRGC) 7.

2 Background

The PCA finds the minimum mean squared error linear transformation that maps from

the original N -dimensional data space into an M-dimensional feature space (M < N)

to achieve dimensionality reduction using large eigenvalues. The resulting basis

vectors can be computed by

(1)

where S

denotes the total scatter matrix. Figure 1 shows examples of Eigenfaces

generated from the generic training images of FRGC data after normalization of the

face images.

Fig. 1. Eigenfaces generated from the FRGC data sorted by the largest eigenvalues; 1

and 2

row images show first 12 eigenvectors, 3

row images show 201 ~ 206 eigenvectors and 4

row images show 501~506 eigenvectors with small eigenvalues; Eigenvectors do not look like

human faces can be discarded in order to achieve dimensionality reduction.

The LDA is another commonly used method which determines a set of discriminant

basis vectors so the ratio of the between-class scatter and the within-class scatter is

maximized. The optimal basis vectors can be denoted as

(2)

]...[||maxarg

21 mT

wwwWSW ==

opt

]...[

maxargW

21opt m

www

WSW

where

S and

S indicate the between-class scatter matrix and the within-class scatter

matrix, respectively. The solution can be solved by the generalized eigenvalue

problem,

(3)

and the final solution becomes the standard eigenvalue problem if S

is invertible.

(4)

Due to the fact that the number of training images is smaller than the number of pixels,

the within-class scatter matrix S

is singular causing problems for LDA. Fisherfaces

first performs PCA to reduce the dimensionality and thus overcome this singular-

matrix problem and applies LDA in the lower-dimensional subspace. The projection

vectors from Fisherfaces are given as follows.

(5)

where c is the total number of class.

On the other hand, the DLDA derives eigenvectors after simultaneous diagonalization

8. Unlike previous approaches, the DDLA diagonalizes

first and then

diagonalizes

S which can be shown as follows

Λ==

WWSIWWS ,

(6)

The smallest eigenvalues in the

can be discarded since they contain no

discriminative power, while keeping small eigenvalues in the

S , especially 0’s.

On the other hand, the GSLDA method avoids inverse or diagonalization approaches

in LDA. The GSLDA approach calculates the orthogonal basis vectors in

(7)

where indicate the null spaces and the upper bars indicate the

orthogonal complement spaces of S

and S

, respectively. The GSLDA method has

been seen to offer better performance over Fisherfaces and other LDA methods 4, and

LDA methods typically outperform PCA based methods 2. Figure 2 shows examples

of the LDA basis vectors generated from the generic training images of the FRGC

data.

Fig. 2. The LDA basis vectors; 1

row images are examples of the Fisherfaces, and 2

row

images are examples of the GSLDA eigenvectors.

2.1 Advanced Correlation Filters

Correlation filter approaches represent the data in the spatial frequency domain. One

of the most popular correlation filters, the minimum average correlation energy

(MACE) 7 filter is designed to minimize the average correlation plane energy

,...m,iwSwS

iWiiB

21,

iiiBW

wwSS

−1

)0(),0(

]...[

maxarg

121 −

pcaW

pca

pcaB

pca

www

WWSWW

opt

]...[||maxarg

21 cNT

pca

wwwWSWW

−

)0()0(

________

SS ∩

resulting from the training images, while constraining the value at the origin to pre-

specified values. Correlation outputs from MACE filters typically exhibit sharp peaks

making the peak detection and location relatively easy and robust. The closed form

expression for the MACE filter vector h is

uΧDΧΧDh

-1-1 1

)(

−+

(8)

where X is a d

xN complex matrix and its ith column contains the lexicographically

re-ordered version of the 2-D Fourier transform of the ith training image. D is a

diagonal matrix containing the average power spectrum of the training images

along its diagonal and u is pre-specified values. Optimally trading off between noise

tolerance and peak sharpness produces the optimal trade-off filters (OTF). OTF

filter vector is given by

()

−+−−

hTXXTX u

(9)

where

()

αα

=+−TD C

, 0 ≤

≤ 1 , and C is a d

diagonal matrix whose diagonal

elements C(k,k) represent the noise power spectral density at frequency k. Varying

allows us to produce filters with optimal tradeoff between noise tolerance and

discrimination. It is important to note that when

=1, the optimal tradeoff filter

reduces to the MACE filter in eq. (8) and when

=0, it simplifies to the noise-tolerant

filter in eq. (9). Large peaks denote good match between the test input and the

reference from which the filter is designed. Due to built-in shift invariance and

designed distortion tolerance, correlation filters for biometric verification exhibit

robustness to illumination variations and other distortions 5.

2.2 Support Vector Machines (SVM)

Support Vector Machines 91011 have been successfully applied in the field of object

recognition, often utilizing the kernel trick for mapping data onto higher-dimensional

feature spaces. The SVM finds the hyperplane that maximizes the margin of

separation in order to minimize the risk of misclassification not only for the training

samples, but also for better generalization to the unseen data.

Unlike PCA and LDA methods where the basis vectors are obtained after centering

the data by either the global mean or the individual mean of the class, the SVM does

not require centering the data. Instead, the SVM emphasizes the data close to the

decision boundary, and the projection coefficients can be estimated by the weight

vector w and bias b. Formally, the decision boundary vector w can be obtained by

minimizing the following known as the Primal Lagrangian form.

(10)

where w is the weight vector orthogonal to the decision boundary and b, N, y,

indicate the bias, the total number of data, and the decision value respectively, and α

are the Lagrange multipliers. After differentiation of L respect to w and b, eq. 10 can

be represented by the following the Dual Lagrangian form.

(11)

∑

−+−=

bxybL

]1)([2/1),,( wwww

αα

∑∑∑

===

><−=

jijijii

xxyyabL

111

),,(

ααα

We can also replace with using the kernel trick. The solution

vector w can be denoted as follows depending on whether kernels are applied or not.

(12)

2.3 Challenges in Face Recognition

Unfortunately, the best set of features and algorithms to recognize human faces are

still unknown and many face recognition methods are being developed and evaluated.

The face recognition grand challenge (FRGC) program [12] is aimed at an objective

evaluation of face recognition methods under different conditions, especially in

experiment 4. This experiment 4 is aimed at comparing controlled indoor still images

to uncontrolled (corridor lighting) still images.

The baseline performance from Eigenface method on this data set is 12% verification

rate (VR) at a false accept rate (FAR) of 0.1%. Figure 3 shows an overview of the

FRGC experiment 4. The generic training set contains 12,776 images (from 222

subjects) taken under controlled and uncontrolled illumination. The gallery set

contains16, 028 images (from 466 subjects) under controlled illumination while the

probe set contains 8014 images (from 466 subjects) under uncontrolled illumination.

Instead of generating basis vectors from the gallery sets, the participants in the FRGC

are supposed to generate basis vectors from the generic training set to assess the

generalization power. Then, the dimensionality of the gallery images and probe

images can be reduced via the basis vectors. Finally, the matching score between

gallery and probe sets needs to be presented to assess the performance.

Fig. 3. An overview of the FRGC experiment 4.

The LDA based methods offer the potential produce better performance over

Eigenfaces. However, the LDA based vectors may not have generalization power to

the unseen classes, since they are optimized based on classes shown previously. This

problem also occurs when we apply the correlation filters since the typical design of

correlation filters is based on the gallery images. The class-dependence feature

analysis (CFA) is proposed to generalize the correlation filters as explained in the

next subsection.

3 Class Dependence Feature Analysis (CFA)

In CFA approach, one filter (e.g., MACE filter) is designed for each class in the

generic training set. Then a test image y is characterized by the inner products of that

test image with the n MACE filters, i.e.

xx ,

)(),(

∑∑

Φ==

iiiiii

xyxy

)(,

αα

(13)

where h

mace-n

is a filter gives small correlation output for all classes except for class-n.

For example, the number of filters generated by the FRGC generic training set is 222

since it contains 222 classes. Then each input image y is projected onto those basis

vectors and x contains the projection coefficients with the dimensionality of 222.

Then the similarity of the probe image to the gallery image is based on the similarity

between the corresponding class-dependent feature vectors. Figure 2 shows examples

of the CFA basis vectors generated from the FRGC generic training data.

Fig. 4. The CFA algorithm; the filter response of y

and h

mace-2

can be distinctive to that of y

and h

mace-2

Fig. 5. The CFA basis vectors for dimensionality reduction.

3.1 Nonlinear Feature Representation

Due to the nonlinear distortions in human faces, the linear subspace methods have not

performed well in real face recognition applications. As a result, the PCA and LDA

algorithms are extended to represent nonlinear features efficiently by mapping onto a

higher dimensional space. Since nonlinear mappings increase the dimensionality

rapidly, kernel approaches are used as they enable us to obtain the necessary inner

products without computing the actual mapping on to the high dimensional space.

Kernel Eigenfaces and Kernel Fisherfaces 13 are proposed to overcome this problem

using the Kernel PCA and Kernel Discriminant Analysis (KDA) 14. The mapping

function can be denoted as follows.

(14)

Kernel functions defined by can be used without having to

form the mapping as long as kernels form an inner product and satisfies Mercer’

theorem 14. Polynomial kernel (

babaK )1,(),( +><=

), Radial Basis Function style

yy ]...[

n-mace2-mace1-mace

hhhHx ==

→Φ :

< )(),(),( yxyxK

kernel (

)2/)(exp(),(

babaK −−=

), and Neural Net style Kernel

(

),tanh(),(

−><= bakbaK

) are widely used.

3.2 Kernel CFA (KCFA)

The Kernel CFA algorithm can be extended from the linear CFA method using the

kernel tricks. The correlation output of a filter h and an in

ut y can be expressed as

(15)

where

XDX

0.5 ' −

indicates pre-whitened version of

. From now on, we assume

the

is already pre-whitened. After mapping onto a high dimension space, the

solution becomes

(16)

These MACE filters based kernel approaches can be extended to include noise

tolerance as in eq. 9. By replacing D by T, where

(

)

αα

=+−TD C

, the new kernel

OTF filters show some noise tolerance depending the parameter

. The resulting

output for the KCFA approaches can be thought as correlation output in the high

dimensional space with tolerating some level of distortions.

3.3 Experimental Results

The performance of a face recognition algorithm can be measured by its false

acceptance rate (FAR) and its false rejection rate (FRR). FAR is the percentage of

imposters wrongly matched. FRR is the fraction of valid users wrongly rejected. A

plot of FAR vs FRR (as matching score threshold is varied) is called a receiver

characteristic (ROC) curve. The verification rate (VR) is 1-FRR, often the ROC may

show VR vs. FAR. Since the FAR can be more problematic in practical face

recognition applications, the FRGC program compares the verification rates at 0.1 %

FAR. Figure 6 shows the experimental results using Eigenfaces (PCA), GSLDA,

CFA, and KCFA of the experiment 4 of the FRGC. The performance of Eigenfaces is

provided by the FRGC teams. The similarity or distance measure between gallery

image and probe image is important. Commonly used distance measures are L1-norm,

L2-norm 6 and Mahalanobis distance. Those distance measures may not perform well

depending on different algorithms. The normalized cosine distance (given below)

exhibits the best results on the CFA and KCFA.

||)y|| ||xy)/(||-(xy)d(x,

⋅

(17)

where d denotes the similarity (or distance) between x and y. Based on the similarity

measure, the identities are claimed using the nearest neighbour rule. The PCA and

GSLDA use the L2-norm while the CFA and KCFA use the distance in eq. 17, and

the resulting performance is shown in Figure 6.

uX))XX))(yh)

−

Φ⋅ΦΦ⋅Φ=Φ⋅Φ

),(),(

()(()((()(

jii

xxKxyK

uXXX

uX)DXDXDD

uX)DX(XDh

'''

0.5-0.5-0.5-0.5-

-1-1-1

))((

)(()(

−

⋅⋅=

⋅=⋅

0,1

0,2

0,3

0,4

0,5

0,6

Ex p 4

Verification Rates

PCA

GSLDA

CFA

KCFA

Fig. 6. The performance comparisons of the FRGC experiment 4 at 0.1 % FAR. The Kernel

CFA shows the best results over all linear methods.

4 Distance Measure in SVM Space

If we can design a decision boundary to separate one face class (with all its

distortions) from all other classes, we can achieve robust face recognition in real

applications. However, it is not an easy task to design those decision boundaries

under all possible distortions. Therefore, a direct use of the SVM as a classifier may

produce worse performance under those distortions since only small number of

training images are allowed to build the SVM. In stead of using the SVM as a

classifier directly, we use the projection coefficients of KCFA features in the SVM

space. Figure 7 shows an example of the decision boundary and distance measure in

the SVM space.

Fig. 7. The decision boundary of a class and distance measure in the SVM space; A direct use

of the SVM may falsely indicate that image C

as not the same person with those images inside

the decision boundary.

The L2-norm distance without the SVM decision boundary w may be large between

the same classes causing poor performance. In this case, the L2-norm distance of C

and C

is greater than that of C

and C

causing a misclassification. However, if we

project C

on to w, the projection coefficients among the same classes will be small

and we can change the threshold distance depending on FAR and FRR. Thus this

approach may lead to flexibility of varying thresholds and better performance in

classification. We apply linear machines, RBF and Polynomial Kernels (PK) in order

to find the best separating vectors varying parameters associated with each kernel

method. The nonlinear SVM such as RBF and PK show better performance over the

linear SVM.

Building the SVM of the face images (of size 128x128 pixels) without any form of

dimensionality reduction is an extremely challenging task. Since the dimensionality

reduction based on KCFA is better than other approaches, we use KCFA features

(222 features) as an input for building the SVM. We design 466 SVMs (in a one-

against all framework) using the gallery set of the FRGC data. The probe images are

then projected on the class-specific SVMs which will provide a similarity score. As

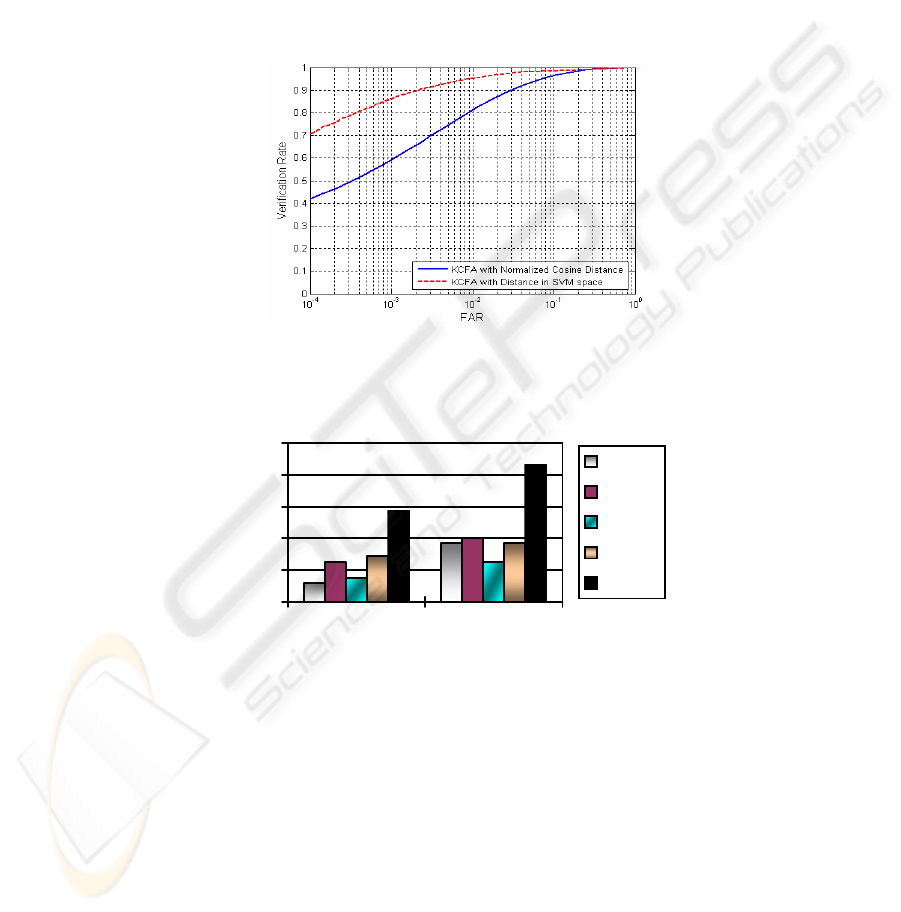
shown in Figure 8, the new distance measure in the SVM space produces better

results than using normalized cosine distance. We also compared the different kernel

approaches such as KPCA and KDA with different distance measure showing the

SVM based KPCA methods have superior to other kernel approaches as shown in

Figure 9.

Fig. 8. VR vs FAR for FRGC experiment 4 for different methods using normalized cosine

distances and SVM space.

0,2

0,4

0,6

0,8

Normalized Cosine L2-SVM Space

Verfication Rates

PCA

KPCA

GSLDA

KDA

KCFA

Fig. 9. VR vs FAR for FRGC experiment 4 using KCFA with different distance measure.

5 Conclusions

Due to nonlinear distortions coupled with blurry images on face images, linear

approaches such as PCA, LDA, and CFA may not represent nor discriminate facial

features efficiently. By using kernel tricks, the Kernel CFA performs dimensionality

reduction showing better performance over all linear approaches. After reducing the

dimensionality of the data, we map the data again onto higher dimension spaces to

build the decision boundaries which separate a class from all classes. Since direct

mapping onto a high dimension using high quality normalized faces (128 by 128

pixels) will be not an easy task, dimension reduction scheme may be necessary before

mapping onto higher dimension where the non-linear features are well represented.

By incorporating the SVM for a new distance measure, the performance gain is

dramatic. These approaches (KCFA, Distance in the SVM space) can be extended

further by adding more databases and may perform robust face recognition in real

applications. Our ongoing work will be conducting the comparison our approaches on

large scale database containing pose changes as well.

References

1. M. Turk and A. Pentland, “Eigenfaces for Recognition,” Journal of Cognitive

Neuroscience, Vol. 3, pp.72-86, 1991.

2. P.Belhumeur, J. Hespanha, and D. Kriegman, “Eigenfaces vs Fisherfaces: Recognition

Using Class Specific Linear Projection,” IEEE Trans. PAMI, Vol.19. No.7, pp.711- 720,

1997.

3. L.F. Chen, H.Y.M. Liao, M.T. Ko, J.C. Lin, and G.J. Yu, “A new LDA-based face

recognition system which can solve the small sample size problem,” Pattern Recognition,

Vol. 33, pp. 1713-1726, 2000

4. W. Zheng, C. Zou, and L. Zhao, “Real-Time Face Recognition Using Gram-Schmidt

Orthgonalization for LDA,” IEEE Conf. Pattern Recognition (ICPR) , pp.403-406, 2004

5. M. Savvides, B.V.K. Vijaya Kumar and P. Khosla, “Face verification using correlation

filters,” Proc. Of Third IEEE Automatic Identification Advanced Technologies, Tarrytown,

NY, pp.56-61, 2002.

6. C. Xie, M. Savvides, and B.V.K. Vijaya Kumar, “Redundant Class-Dependence Feature

Analysis Based on Correlation Filters Using FRGC2.0 Data,” IEEE Conf. Computer Vision

and Pattern Recognition(CVPR) , 2005

7. A. Mahalanobis, B.V.K. Vijaya Kumar, and D. Casasent, “Minimum average correlation

energy filters,” Appl. Opt. 26, pp. 3633-3630, 1987.

8. K. Fukunaga, “Introduction to Statistical Pattern Recogniton (2

Edition)”, New

York:Academic Press, 1990

9. V. N. Vapnik, The Nature of Statistical Learning Theory, New York: Springer-Verlag,

1995.

10. B. Schölkopf, Support Vector Learning, Munich, Germany: Oldenbourg-Verlag, 1997.

11. P. J. Phillips, “Support vector machines applied to face recognition,” Advances in Neural

Information Processing Systems 11, M. S. Kearns, S. A. Solla, and D. A. Cohn, eds., 1998.

12. P. J. Phillips, P. J. Flynn, T. Scruggs, K. W. Bowyer, J. Chang, K. Hoffman, J. Marques, J.

Min, and W.Worek, "Overview of the Face Recognition Grand Challenge,” IEEE Conf.

Computer Vision and Pattern Recognition(CVPR), 2005

13. M.H Yang, “Kernel Eigenfaces vs. Kernel Fisherfaces: Face Recognition using Kernel

Methods,” IEEE Conf. Automatic Face and Gesture Recognition, pp. 215-220, 2002

14. K.R. Muller, S.Mika, G. Ratsch, K. Tsuda, and B. Scholkopf , “An Introduction to Kernel-

Based Learning Algorithms,” IEEE Trans. Neural Network, Vol.12, No.2, pp.181-202, Mar

2001.