PREDICTING CARDIOVASCULAR RISKS
Using POSSUM, PPOSSUM and Neural Net Techniques
Thuy Nguyen Thi Thu, D. N. Davis
Computer Science Department, Hull University,Cottingham Road, Hull, UK.
Keywords: Risk Assessment, POSSUM, PPOSSUM, Neural network.
Abstract: Neural Networks are broadly applied in a number of fields such as cognitive science, diagnosis, and
forecasting. Medical decision support is one area of increasing research interest. Ongoing collaborations
between cardiovascular clinicians and computer science are looking at the application of neural networks
(and other data mining techniques) to the area of individual patient diagnosis, based on clinical records
(from Hull and Dundee sites). The current research looks to advance initial investigations in a number of
ways. Firstly, through a rigorous analysis of the clinical data, using data mining and statistical tools, we
hope to be able to extend the usefulness of much of the clinical data set. Problems with the data include
differences in attribute presence and use across different sites, and missing values. Secondly we look to
advance the classification of referred patients with different outcome through the rigorous use of POSSUM,
PPOSSUM and both supervised and unsupervised neural net techniques. Through the use of different
classifiers, a better clinical diagnostic support model may be built.
1 INTRODUCTION
Assessing patient risk in medical domains is of
crucial importance. The research reported in this
paper considers the domain of cardiovascular
medicine. No gold standard exists for assessing the
risk of individual patients. Current techniques use a
generic technique applied to the patient’s
cardiovascular record. This data itself is inconsistent
over a history of patients at any one clinical site, and
not always immediately useable. Our research is
applying data mining methods to make the clinical
data more useable, meaningful and open to the use
of neural and other classifier techniques.
The Physiological and Operative Severity Score
for the enUmeration of Mortality and morbidity
(POSSUM), first used by Copeland et al (1991), is
applied to predict the clinical outcome for general
surgical patients. In this paper, we use data which is
to be evaluated by POSSUM and PPOSUM via a-
priori scoring on physiological state and operative
severity. The equations used for calculating the
POSSUM produces scores for the expected patient
mortality and morbidity. The performance of these
two techniques will be measured through a
comparison of the ratio of the predicted mortality for
all patients and observed dead patients.
The POSSUM and PPOSSUM models are built
assuming a linear relationship between the outcome
and other variables. It is not clear how well
grounded this assumption is. More over, the linear
models are compromised through missing or noisy
data. The advance from using neural network has
enabled non linear analysis for diagnostic purposes
(Turton et al, 2000).
Neural Networks are applied in broad areas of
society such as pattern recognition, biomedical
system. More over, Neural Networks can be used
experimentally to model the human cardiovascular
system (Siganos, 1996). The diagnosis can be
achieved by building a model of the cardiovascular
system of an individual and comparing it with the
real time physiological measurements taken from the
patient.
The use of different neural network techniques
such as MultiLayer Perceptron (MLP), Radial Basic
Function (RBF), and Support Vector Machine
(SVM) are tried with the aim of improving the
performance of clinical decisions. In this paper, the
given data is transformed to the appropriate format
230
Nguyen Thi Thu T. and N. Davis D. (2006).
PREDICTING CARDIOVASCULAR RISKS - Using POSSUM, PPOSSUM and Neural Net Techniques.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 230-234
DOI: 10.5220/0002494202300234
Copyright
c
 SciTePress

for these neural network techniques. The data
includes the physiology and operative scoring
attributes, plus other relevant attributes useful in
predicting patient risk.
2 POSSUM AND PPOSSUM
SYSTEM
The Physiological and Operative Severity Score for
enUmeration of Mortality and morbidity (POSSUM)
is an appropriate scoring system for risk-adjusted
comparative general surgical audit. According to
Jones and Corssat (1999), POSSUM i
s the most
appropriate of the recently available scores for general
surgical practice.
This scoring algorithm has been
used widely in the UK, but application of POSSUM
in other countries has been limited (Yii and Ng,
2002). It relies on an a-priori scoring of
physiological and operative severity parameters,
based on a multivariate discriminant analysis of
factors measured in a broad group of general
surgical patients (Copeland et al, 1991).
The logistic regression analysis in this model
tries to produce statistically significant equations for
both mortality and morbidity based on a 12 factors/4
grades physiological score and 6 factors operative
severity score (Copeland et al, 1991). The Predicted
Morbidity Rate is given by:-
R
1
= 1/(1+ e
-x
)
where x = (0.16* physiological score)
+ (0.19* operative score) - 5.91;
The Predicted Mortality Rate is given by:-
R
2
= 1/(1+ e
-y
)
where y = (0.13* physiological score)
+ (0.16* operative score) - 7.04;
There is a further model based on POSSUM, called
Portsmouth POSSUM (P-POSSUM). This equation
was derived from a heterogeneous general surgical
population and has been used as an audit tool to
provide risk-adjusted operative mortality rates. The
Predicted Death Rate is given by
R = 1 / (1+ e
-z
)
where z = (0.1692 * physiological score)
+ (0.1550 * operative score) - 9.065
Experiment
The data used in this paper is already scored for the
physiological and operative severity attributes. We
use the equations of POSSUM to predict the
morbidity and mortality for each patient. Patients
were divided into groups according to their predicted
mortality rate: 0-10, 10-20,20-30,30-40,40-50, and
greater than 50%. The Mean predicted risk of
Mortality presents the average risk for patients in
each range. For example, the average mortality risk
for patients in the first group (less than 10%) is 7%.
No of operations is the number of patients in each
group. Predicted death (E) is the number of dead
patients, which are predicted by POSSUM. The
Reported deaths (O) is the number of actual dead
patients in each group. The performance of the
system is measured by the ratio of observed to
predicted mortality (O/E). The discrepancy between
the presented O/E rate and the O and E values in the
table is due to the numbers for O and E being
presented as rounded to the nearest integer.
Table 1 below shows the mean predicted risk of
mortality in 7 groups of patient, and the comparisons
between predicted and observed mortality for the
POSSUM system.
Table 1: Comparison of observed and predicted death
from POSSUM logistic equations
.
Range
of
predicte
d death
rate
Mean
predicted
risk of
Mortality
(%)
No of
operatio
ns
Predict
ed
deaths
(E)
Report
ed
deaths
(O)
The
ratio
O/E
0-10% 7 130 9 9 0.99
10-20% 15 81 12 19 1.57
20-30% 25 31 8 2 0.26
30-40% 36 9 3 0 0
40-50% 43 15 6 5 0.78
>50% 62 5 3 3 0.97
0-100% 15 265 41 38 0.93
The performances of the PPOSSUM method for
predicting the mortality rates can be seen in table 2
below. The ratio between observed and expected
number of adverse outcome indicates the prediction
performance. A ratio of 1 indicates that there is an
average performance; greater than 1 means the
performance is worse than expected; and less than 1
means the performance better than expected
predictions.
PREDICTING CARDIOVASCULAR RISKS - Using POSSUM, PPOSSUM and Neural Net Techniques
231

Table 2: Comparison of observed and predicted death
from PPOSSUM logistic equations
.
Range of
predicted
death
rate (%)
Mean
predicted
risk of
Mortality
(%)
No of
operations
Predicted
deaths
Reported
deaths
The ratio
(O/E)
0-10 3 222 8 30 3.75
10-20% 14 24 3 2 0.67
20-30% 23 12 3 2 0.67
30-40% 33 4 1 3 3.00
40-50% 44 2 1 2 2.00
>50% 57 1 1 0 0.00
0-100 6 265 17 38 2.24
For example from table 1, the ratio (O/E) for the
range of predicted death rate of 20-30% is 0.26. This
means the performance of operation is better than
predicting operation. However, the ratio for the
range of 10-20% is 1.57. This means the
performance of operations is worse than predicting
operation.
Overall POSSUM gives close to accurate risk
estimation, with a O/E ratio of 0.93. However its
performance varies across the different risk
categories, and is particularly poor for low risk
operations (10-20% bands). Overall PPOSSUM
underestimates the risk (O/E = 2.24), and for no one
group does it give an accurate risk estimation. The
need for better estimators is therefore obvious.
3 NEURAL NETWORK
TECHNIQUES
The Neural Network (NN) approach adopted is that
of an information processing system that consists of
a graph representing the processing system as well
as various algorithms which access that graph
(Dunham, 2002). The Neural network can be viewed
as a directed graph with source (input), sink
(output), and internal (hidden) nodes. Neural
Network techniques can be divided into two
methodologies: supervised learning and
unsupervised learning. For supervised learning, the
data is trained via networks with expected (a-priori
defined) outputs. The supervised techniques used are
Multi-Layer Perceptron (MLP), Radial Basis
Function (RBF), and Support Vector Machine
(SVM). Conversely, with the unsupervised method,
no a-priori classifications are used. Experimentation
has identified potentially useful techniques such as
Self Organizing Maps (SOM), and clustering using
Principal Component Analysis (PCA). In the
experiments described in this paper, we used
supervised neural techniques.
The original data includes 265 patterns with 86
attributes. The given data includes attributes from a
clinical scoring system for physiological status, and
operative severity. However the data needs to be
prepared in order to be appropriate for use with the
different networks.
First of all, the data is transformed to numerical
data in the range [0,1]. This is straight-forward
Boolean attributes. Continuous values are mapped
onto the same range using a linear transform. The
nominal attributes are transformed to a number of
Boolean valued sub-attributes. The number of sub-
attributes dependent upon how many values they
take. For example, the Carotid disease attribute has
10 values, so the number of new sub-attributes is 10.
Missing values are replaced by a standard “Null”.
By eliminating irrelevant attributes, the transformed
data set has 83 attributes with 265 patterns.
Experiments
In the first experiments using neural network
techniques, they are compared with POSSUM as a
means for predicting mortality rates. WEKA
software is used to develop the different neural
classifiers to be applied. In this software, the
alternative functions of Neural Network can be
easily chosen. More over, detailed parameters such
as number of layers, the learning rate, etc. for each
technique can be changed. In general, the number of
layers is 3 with 86 inputs, 42 hidden nodes, and 1
output node. This paper does not detail the effect of
alternative parameter values for each technique, but
presents best results for each neural technique. For
example, in MLP, the chosen learning rate is 0.3, the
iteration is 500. The data set is split in two ways. A
test set is taken by using 50% of the overall pattern
set or using a 10 fold cross validation partition. With
the latter technique, the data set is divided into 10
partitions. One partition is used as a test set whilst
the rest is for training; the procedure is repeated 10
times, so that each partition acts as a separate test
set.
The cleaned data has a mortality rate of 14.34%
(38 from 265 patterns with status= “dead”). The
accuracy results are obtained through the generation
and analysis of a confusion matrix. The results are
compared to the predictions given in tables 1 and 2.
Overall, the predicted mortality rate for each neural
network technique was lower than observed one (see
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
232

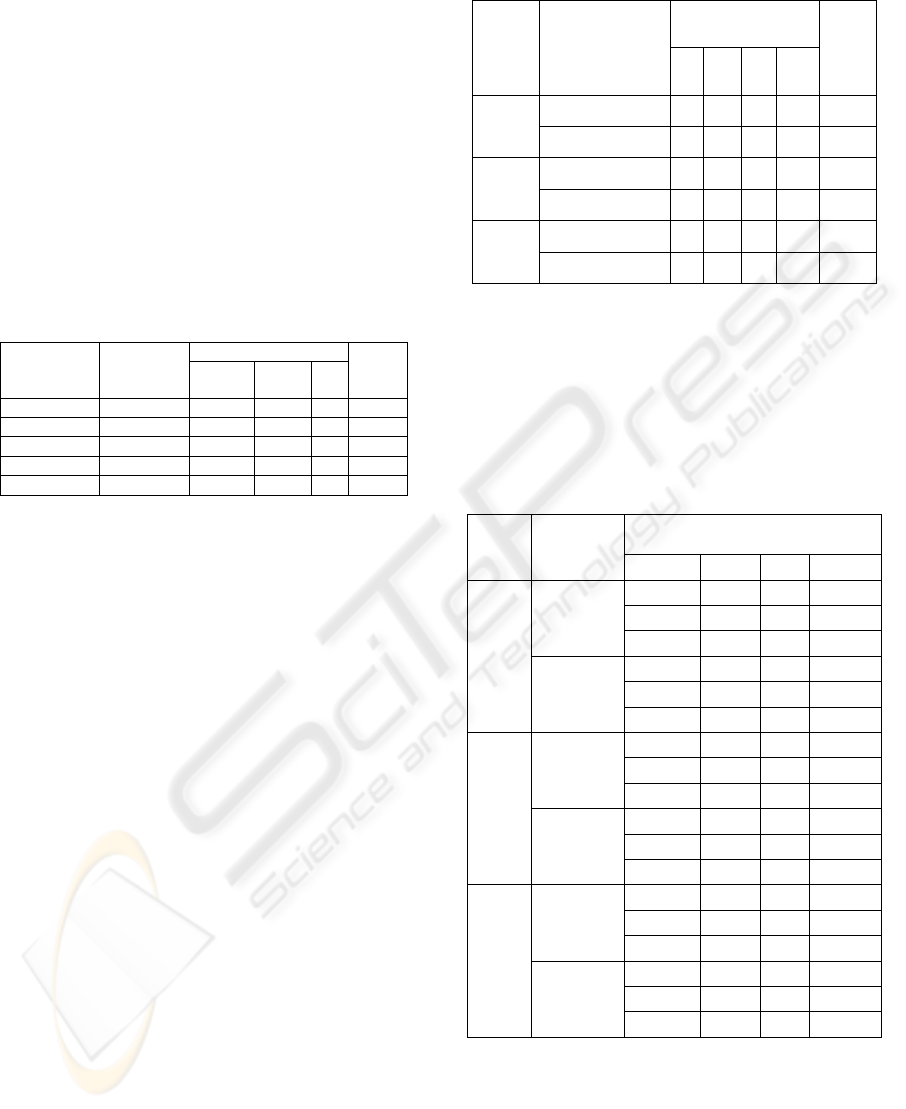
detail in table 3 below). Percentage misclassification
for each model is obtained by dividing the sum of
the misclassification of “dead” or “alive” patient by
the total number of patterns. The results show that
although POSSUM gives a better result for the ratio
of observed and expected death, its misclassification
is the highest. For medical domains a pessimistic
predictor is more tolerable (it is better to predict
False Positives than False Negatives) but a reduction
in misclassification would help in reducing clinical
work load. We therefore look to evaluating risk in
terms other than mortality.
Table 3: The comparison of results of experiments with
supervised neural network techniques, POSSUM and
PPOSSUM for 265 patients
.
Misclassification Models Predicted
deaths (O)
Dead Alive %
The
ratio
(O/E)
POSSUM 41 32 29 23 0.9
PPOSSUM 17 11 32 16 2.25
MLP 15 23 12 13 2.53
RBF 0 38 0 14 N/A
SVM 11 28 13 15 3.45
To ensure the provision of highest quality of care
a comparative audit of the data, different outcomes
can be investigated. Patient parameters such as
stroke, myocardial relapse within 30 day of
operation (30Day_MR), and cardiovascular arrest
within 30 days (30Day_CVA) may be used as
indicators for outcome risk for individual patients.
Subsequently a new summary output attribute (risk)
is built based on the value for the two main post-
operative outputs. This attribute takes three values
(High (H), Medium (M), Low (L)) based on the
heuristic rules:
Σ(Status, 30Day_MR) = 0 → Risk =L
Σ(Status, 30Day_MR) = 1 → Risk =M
Σ(Status, 30Day_MR) = 2 → Risk=H
The results can be seen in table 4. If
misclassification rate were used to differentiate
between the two training methods, it is evident from
table 4 that cross validation outperforms 50% split in
terms of both misclassification rate and Mean
Squared Error (MSE). From table 4, the MLP model
provides the best predications of patient risk with a
MSE, and a misclassification (0.02, 3.7% with type
1, 0.01, 1.9% with type 2 respectively).
Table 4: The comparisons of neural network techniques.
Misclassification NN
Model
Test set
L M H %
MSE
50% split 0 5 0 3.7 0.02 MLP
Cross validation 0 2 3 1.9 0.01
50% split 0 7 3 7.5 0.05 RBF
Cross validation 0 4 6 3.8 0.03
50% split 0 2 0 1.5 0.08 SVM
Cross validation 0 2 3 1.9 0.07
However as the analysis for the results given in
Table 3 made clear, misclassification alone is
insufficient as an indicator of classifier suitability for
medical domains. To explain the misclassification
in table 4, table 5 below shows more detail about
confusion matrix of each NN model.
Table 5: Results from confusion matrix for alternative NN
models
.
Confusion matrix of Risk NN
Model
Test set
L M H
L 110 0 0
M 4 15 1
50% split
H 0 0 3
L 227 0 0
M 0 30 2
MLP
Cross
validation
H 0 3 3
L 110 0 0
M 7 13 0
50% split
H 1 2 0
L 227 0 0
M 3 28 1
RBF
Cross
validation
H 2 4 0
L 110 0 0
M 1 18 1
50% split
H 0 0 3
L 227 0 0
M 0 50 2
SVM
Cross
validation
H 0 3 3
From table 5, RBF has the worst classification
compared to other models because almost medium
and high risk patients are misplaced into lower
levels of risk. For example, the 3 high risk patients
are misplaced into low risk (1), and medium risk (2)
with 50% split of test set. The preferred
misclassification is if patients are attributed with a
PREDICTING CARDIOVASCULAR RISKS - Using POSSUM, PPOSSUM and Neural Net Techniques
233

higher level of risk. On this basis, the best classifier
in Table5 is the Support Vector Machine (SVM)
trained using 50% split.
4 CONCLUSIONS AND FURTHER
WORKS
POSSUM and PPOSSUM are generic clinical tools
that allow a metric factor to be used in assessing the
severity of illness. The risk assessments are
compared to reported mortality across a group of
patients. The ratio between the predictions of
POSSUM, PPOSSUM and the observed mortality
shows the performances of the system. However,
each individual patient has an assessment of risk,
which is based on clinical judgement. The value of
the scoring system quantifies the risks of patient, and
these risks can be compared to the reported ones
(Jones & Cossart, 1999).
POSSUM and PPOSSUM seem to over predict
mortality for the data. These models are restricted to
predictions of mortality, morbidity and death rates.
For cardio vascular disease the combination of other
outcomes such as 30 day MR or stroke or dead may
give rise to more appropriate measures of risk.
By using a confusion matrix, the
misclassification of each model is evaluated. From
table 3 and table 4 it seems that using different
models of neural network produces smaller
misclassification errors than with POSSUM, and
PPOSSUM. More interestingly, the models using the
new outcome of risk (High, Medium, Low) had the
smallest percentage of misclassification compared to
the other risk predication models (i.e. mortality or
morbidity). The bias of misclassification for each
neural network models needs to be subjected to
further investigation. More over, a comparison of
supervised versus unsupervised classifiers may help
in determining more appropriate patient
classifications. These results can then be applied in
determining what of the original data should be used
to generate a better set of classifiers and indicators
of use in predicting cardio vascular risk.
The selection of input attributes for patient
classification is an issue for this and further work.
The set of attributes, and their value ranges, can be
made small enough they will reduce the
complication of developing classifiers for the
domain. The domain independent attribute and data
reduction techniques will be developed from the
theory of mutual information (Cover & Thomas,
1991). If the domain derived techniques are not to be
trusted or are to be independently validated, then
alternative means of clustering patients (according to
risk) are required. We will use unsupervised neural
techniques of various types to achieve this.
ACKNOWLEDGEMENTS
Thank you to the Clinical Biosciences Institute,
University of Hull and the Institute for Systems and
Technologies of Information, Control and
Communication for support funding.
REFERENCES
Copeland G P, Jones D, Walters M. (1991). POSSUM: a
scoring system for surgical audit. British Journal
Surgery, 78, 355-360.
Copeland G P. (2002). The POSSUM system of surgical
audit. Archives of Surgery, 137, 15-19.
Cover, T. M., Thomas, J. A. (1991). Elements of
Information Theory. New York, Wiley.
Dunham, M. H. (2002). Data Mining Introductory and
Advance Topics. Upper Saddle River, NJ, Prentice
Hall/Pearson Education.
Jones H.J.S, & Cossart de L., (1999) Risk scoring in
surgical patients. British Journal Surgery, 86, 149-
157.
Siganos, D. (1996). Neural Networks in Medicine.
Retrieved January 9, 2006 from:
http://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol2/
ds12/article2.html
Turton E. P., Scott D. J., Delbridge M., Snowden S., &
Kester R. C. (2000). Ruptured abdominal aortic
aneurysm: a novel method of outcome prediction
using neural network technology. European Journal of
Vascular and Endovascular Surgery 19(2), 184-9.
WEKA software (University of Waikato, New Zealand,
version 3.4.5). (n.d.). Retrieved January 9, 2006 from
http://www.cs.waikato.ac.nz/~ml/weka/index.html
Witten, I.H., & Eibe F. (1999). Data Mining: Practical
Machine Learning Tools and Techniques with Java
Implementations. Morgan Kaufmann.
Yii M. K., and Ng K. J., (2002), Risk-adjusted surgical
audit with the POSSUM scoring system in a
developing country, British Journal of Surgery,
89:110-113.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
234