A MULTIDIMENSIONAL APPROACH TO THE

REPRESENTATION OF THE SPATIO-TEMPORAL

MULTI-GRANULARITY

Concepción M. Gascueña, Dolores Cuadra, Paloma Martínez

Computer Science Department University Carlos III Madrid, Avenida de la Universidad 30 Leganés 28911 Spain

Keywords: Multidimensional model, Spatio-temporal Database, Spatio-temporal multi-granularity representation,

Spatial Datawarehouse.

Abstract: Many efforts have been made to the treatment of spatial data in databases both in traditional database

systems and decision of support systems or On-Line Analytical Processing (OLAP) technologies in

datawarehouses (DW). Nevertheless, many open questions concerning this kind of data still remain. The

work presented in this paper is focused on dealing with the spatial and temporal granularity within a logical

multidimensional model. We propose an extension of the Snowflake model to gather the spatial data and to

show our proposal to represent the spatial evolution through time in a simple and intuitive way. We

represent the temporal and spatial multi-granularity with different levels in the hierarchies of dimensions,

and we present a typology of hierarchies to include more semantics in the Snowflake scheme.

1 INTRODUCTION

Many works have addressed the study of the

treatment of spatial data and its management in

Database to avoid inconsistencies caused by

Geographic Information Systems (GISs), which

make a heterogeneous treatment of data separating

spatial data and storing them in file systems and

non-spatial data, in general, stored in database

systems. Nevertheless, these are still many questions

unresolved when managing this singular data. One

of these questions is derived from the use of spatial-

temporal data and is related to the granularity

definition. The spatial granularity is defined as the

unit of measure chosen to represent the spatial

element within a given reference system. The

temporal granularity is defined to represent the

variations of an element, through time. The spatial-

temporal multi-granularity represents the units of

measurement chosen to store a geometric object in

different moments of time. Many studies measure

time in intervals, but in our proposal we will use

points in time which, due to their simplicity, avoid

the problem of coalescence. The main objective of

this proposal is to enrich the Multidimensional

models from a logical point of view to include

semantics and information about spatio-temporal

data. We propose an extension of the Snowflake

scheme to gather both the spatial granularity and the

temporal granularity. This paper is organized as

follows: Section 2 contains references to works

related to the treatment of the spatial and temporal

data in databases. Section 3 contains logical

multidimensional concepts. Section 4 is made a

proposal for the multi-granular treatment using the

Snowflake scheme. Section 5 presents several

examples to clarify our proposal and some

conclusions are given in section 6.

2 RELATED WORKS

There is a great amount of research about the special

characteristics of the spatial data and its

representation in Multidimensional schemes.

(Sefanovic et al., 2000) distinguish between three

types of spatial dimensions, according to whether

the spatial elements are include in every hierarchy,

in some hierarchy or in no hierarchy. Also they

consider two types of measures, spatial and

numerical. (Miquel et al.,2004) establish that if a

spatial measure is required in the fact table, then the

model must include a spatial dimension, as opposed

175

M. Gascueña C., Cuadra D. and Martínez P. (2006).

A MULTIDIMENSIONAL APPROACH TO THE REPRESENTATION OF THE SPATIO-TEMPORAL MULTI-GRANULARITY.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 175-180

DOI: 10.5220/0002495801750180

 SciTePress

to (Malinowski and Zimanyi , 2004) who propose

the inclusion of the spatial data in the different

levels of a hierarchy and also in measures. (Rives et

al., 2001), study the spatial data in the dimensions

and in the fact table. (Kouba et al. 2002) treat the

navigation consistency among the levels of the

hierarchies for spatial data and OLAP systems. (Han

et al., 1997), establish Spatial On-Line Analytical

Processing (SOLAP) prototypes that gather the

concepts of OLAP and apply them to spatial data.

The proposal of (Pourabbas et al.) and (Ferri et al.,

2000) integrates GIS systems and DW/OLAP

environments. None of these approaches define the

spatio-temporal multi-granularity concept.

According to (Camossi, et al.,2003) the spatio-

temporal multi-granularity concept is very important

in representing the semantic of domain.

3 MULTIDIMENSIONAL

CONCEPTS

A Data Warehouse (DW) is defined as a collection

of subject-oriented, integrated, non-volatile data that

vary in time, which support decision making

processes (Sefanovic et al., 2000). DW are usually

represented at a logical level by multidimensional

models and these use Star, Snowflake or the

Constellation scheme. A logical multidimensional

model consists of different elements: dimensions,

hierarchies and fact tables. A fact table contains the

focus of analysis and subject-orientation, e.g.

analysis of daily sales of stores in a city. Also a fact

table contains measures, based on the dimensions,

that reflect a characteristic whose evolution we wish

obtain. In the previous example, the sales are

measures and the stores, the city, and the days are

dimensions. The Dimensions provide a view of the

data from different perspectives and the hierarchies

provide a more generalized view of them. The

dimensions can form hierarchies like Day-Month-

Year and moreover, they can contain attributes that

complete information, such as holidays in a month.

The Star scheme consists of dimensions, without

hierarchies, and a fact table with measures. The

Snowflake scheme permits that the attributes of

dimensions are structured into different groups.

These groups form levels and these levels form a

hierarchy. The Constellation scheme can contain

several fact tables in the scheme, each one with its

corresponding measures and these fact tables can

share it’s hierarchies. Within a hierarchy, the lower

level is called leaf level. The OLAP Systems allow

dynamic manipulation of the DW for the process of

decision making. The SDWs combine DW and

Spatial System Databases and allow storage of huge

volumes of spatial data, spatial statistical analysis

and spatial data mining. We use an extension of the

Snowflake scheme to include spatial data and make

our proposal.

4 INCLUDING

MULTI-GRANULARITY IN A

SNOWFLAKE SCHEMA

We propose a extension of the Snowflake scheme

due to its intuitive manner of representing the

evolution of an object through time. The aim is to

add semantic information to the scheme. We

propose to treat the spatial and temporal granularity

as dimensions in the Snowflake schema.

Table 1: Temporal conversion functions.

It returns, for each granule in the coarser granularity, the value which

always appears in the included granules at the finer granularity if this

value exists, the null value otherwise

All

It returns, for each granule in the coarser granularity, the value which

appears most frequently in the included granules at the finer granularity

Main

First and last index in the Proj (index) function

First,, Last

It returns, for each granule in the coarser granularity, the value corresponding

to the granule of position index at the finer granularity

Proj (index)

It returns, for each granule in the coarser granularity, the value which

always appears in the included granules at the finer granularity if this

value exists, the null value otherwise

All

It returns, for each granule in the coarser granularity, the value which

appears most frequently in the included granules at the finer granularity

Main

First and last index in the Proj (index) function

First,, Last

It returns, for each granule in the coarser granularity, the value corresponding

to the granule of position index at the finer granularity

Proj (index)

In order to operate and compare objects with

different granularity, we must use conversion

functions. Some conversion functions are shown in

Table 1 and Table 2. The application of these

functions guarantees the topology consistency

(Camossi et al., 2003).

Table 2: Patial conversion functions.

It contracts an open line, endpoints included, to a pointl_contr

It contracts a simple connect region and its bounding to a pointr_contr

It eliminates (abstracts) an isolated point inside a regionP_abs

Absorption operations

It eliminates a line inside a regionl_abs

It merges two regions sharing a boundary line into a single regionr_merge

It merges two lines sharing an endpoint into to single linel_merge

Merge functions

It reduces a region and its bounding lines to a liner_thinning

Contract functions

It contracts an open line, endpoints included, to a pointl_contr

It contracts a simple connect region and its bounding to a pointr_contr

It eliminates (abstracts) an isolated point inside a regionP_abs

Absorption operations

It eliminates a line inside a regionl_abs

It merges two regions sharing a boundary line into a single regionr_merge

It merges two lines sharing an endpoint into to single linel_merge

Merge functions

It reduces a region and its bounding lines to a liner_thinning

Contract functions

Table 2.1: Some conversion functions for

multidimensional model.

M_Last

Mr_thinning

Mr_contr

Ml_contr

It chooses the last element within a rank

It reduces a region and its bounding lines to a line

It contracts a simple connect region and its bounding to a point

It contracts an open line, endpoints included, to a point

M_Last

Mr_thinning

Mr_contr

Ml_contr

It chooses the last element within a rank

It reduces a region and its bounding lines to a line

It contracts a simple connect region and its bounding to a point

It contracts an open line, endpoints included, to a point

We propose a notation based on multidimensional

concepts (see Figure1).

ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

176

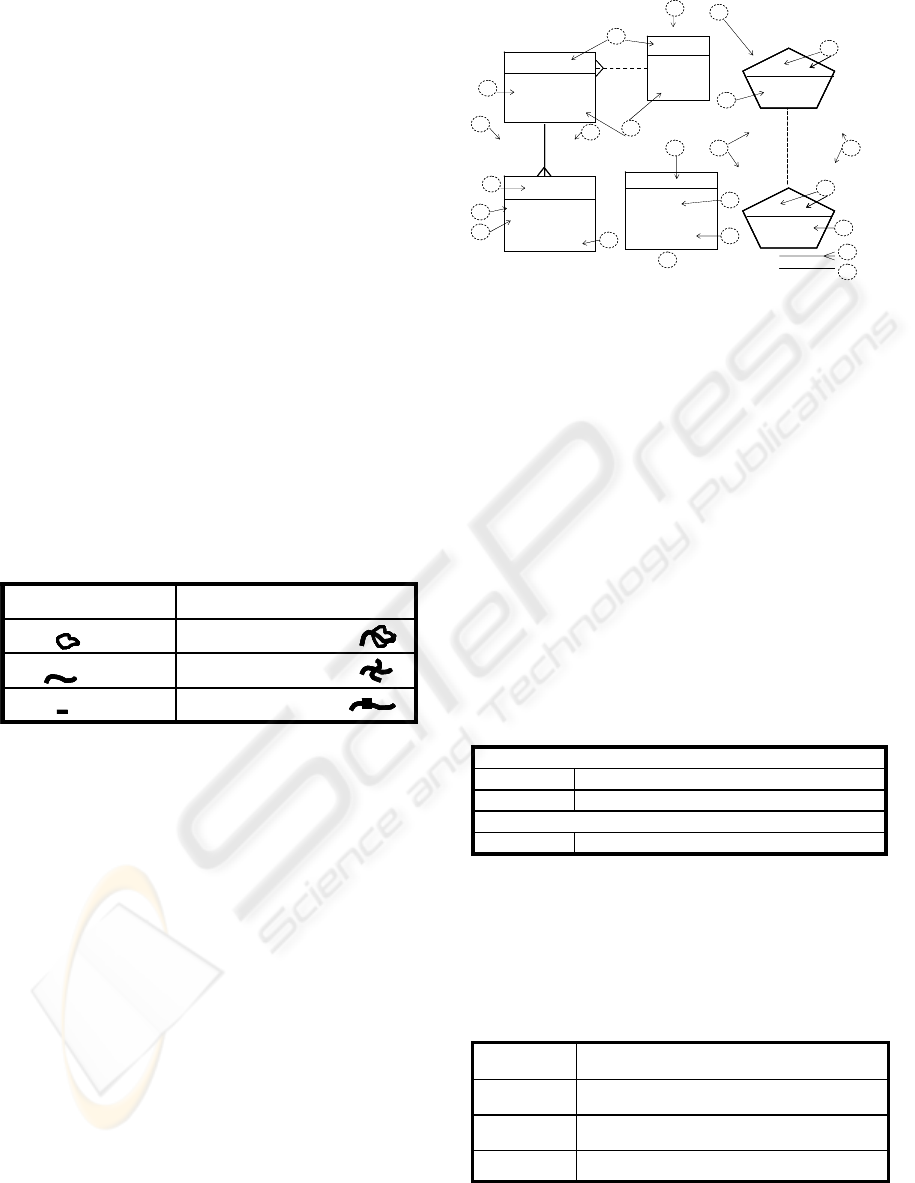
In order to represent the different spatial

granularities, we propose to include a new type of

hierarchy called Static hierarchy. This hierarchy

type is different from the ones used previously by

the multidimensional scheme. Each spatial

granularity will be treated as a level within this

hierarchy.

The Dynamic hierarchy, (figure 1,h), where the

route (navigate) from one level to another implies

changes in measures of the fact table. The Static

hierarchy, (figure 1,i), where the route (navigate)

from one level to another does not imply changes in

measures of the fact tables. Nevertheless, Static

hierarchies contribute semantically to the model and

provide clarity in the study of facts in the decision

making processes.

Each Static hierarchy level, different to leaf level, is

graphically represented by a pentagon (figure 1,o).

We define the granularity within hierarchy as

follows: a granularity g

is finer_than another one

, if g

∈N

and g

∈N

where N

< N

and N

∈J

and J

∈D

where N

and N

are levels of the

hierarchy J

. Where J

is a hierarchy of the D

dimension and also g1 ⊆ g2.

Topological RelationshipaSapatial Data Type

Cros Point and LinePoint

Cross Line and LineLine

Cross Surface and LineSurface

Topological RelationshipaSapatial Data Type

Cros Point and LinePoint

Cross Line and LineLine

Cross Surface and LineSurface

Figure 2a: Some spatial data types and topological

relationships.

The leaf level marks the finer granularity in each

dimension. In order to navegate between different

levels of hierarchies, we use multidimensional

operators, some of these are shown in (Figure 2,b).

To represent the geometry of the spatial data, we use

SQL3 with its extension to spatial data type and the

topological relationships among them, according to

OpenGis Specification (Figura 2,a). In order to show

the conversion function that we wished for when

applying Roll-up in the hierarchy, we introduced a

new label in the scheme. (Figure 1,j) (Figure 1,k).

We think that it is important to express the

aggregation functions used when we navigate

through different levels of hierarchies. Some

funtions are shown in Table3 and Table4.

Leaf Level

Key attibute

Aggregate Function (Measure1)

Key attribute

Secondary attribute

------

Level 1

Key attibute

Dimension with a Dimension with a

Dinamic Hierarchy S tatic Hierarchy

Transformation Function 1(Spatial Measure)

j k

Granularity n Geometry n

Granularity 1 Geometry 1

Transformation Function n(Spatial Measure)

Fact Table

Measure 1

…..

Measure n

Key Dimension 1

-------------

Key Dimension n

Level n

g.1

g.2

g.3

Leaf Level

Key attibute

Aggregate Function (Measure1)

Key attribute

Secondary attribute

------

Level 1

Key attibute

Dimension with a Dimension with a

Dinamic Hierarchy S tatic Hierarchy

Transformation Function 1(Spatial Measure)

j k

Granularity n Geometry nGranularity n Geometry nGranularity n Geometry n

Granularity 1 Geometry 1Granularity 1 Geometry 1Granularity 1 Geometry 1

Transformation Function n(Spatial Measure)

Fact Table

Measure 1

…..

Measure n

Key Dimension 1

-------------

Key Dimension n

Fact Table

Measure 1

…..

Measure n

Key Dimension 1

-------------

Key Dimension n

Fact Table

Measure 1

…..

Measure n

Key Dimension 1

-------------

Key Dimension n

Level n

g.1

g.2

g.3

a) Dimension table of leaf level

b) Dimension table of a dynamic hierarchy

c) Key attributes as primary key of each level

d) Secondary Attributes that complete information of

each level

e) Name of the leaf level

f) Name of level

Fact table: g.1 Fact table name, g.2 Measure, focus

of analysis, g.3 Key from dimensions.

h) Dynamic Hierarchy

i) Static Hierarchy

j) Label expressing the associate function from each

measure in roll-up of dimensions

k) Measure in which function is applied

l) Representation of geometry and units expressed in a

spatial reference

m) The cardinality 1:N, between levels

n) The cardinality 1:1, between levels

o) Represents a level in a static hierarchy

Figure 1: Notation for a Logical Model.

Selection and projection of elementsSlice, Dice

Selecting elements

Navigating from higher level to lower levelDrill-Dow

Navigating from lower level to higher levelRoll-up

Navigating through the levels of hierarchy

Selection and projection of elementsSlice, Dice

Selecting elements

Navigating from higher level to lower levelDrill-Dow

Navigating from lower level to higher levelRoll-up

Navigating through the levels of hierarchy

Figure 2b: Multidimensional Operators.

We distinguish between thematic dimension

which do not contain spatial data and spatial

dimension that contain spatial data.

Table 3: Non Spatial data Functions.

User Defined

Median, most frequent, rank.. Required new calculations using

the data of the leaf level

Holistic

Average, Variance, Standard deviation,…. Need an additional

treatment for reusing the values

Algebraic

Sum, Min, Max…Reuse aggregates of a lower level of a

hierarchy in order to calculate the aggregates for higher level

Distributive

User Defined

Median, most frequent, rank.. Required new calculations using

the data of the leaf level

Holistic

Average, Variance, Standard deviation,…. Need an additional

treatment for reusing the values

Algebraic

Sum, Min, Max…Reuse aggregates of a lower level of a

hierarchy in order to calculate the aggregates for higher level

Distributive

We present our proposal studing the spatial data

within the fact table according to if it is treated as a

measure or as a dimension with some examples: In

A MULTIDIMENSIONAL APPROACH TO THE REPRESENTATION OF THE SPATIO-TEMPORAL

MULTI-GRANULARITY

177

the example 1, we study when spatial data is only

one spatial dimension present in the fact table,

(Figure 3).

In the example 2 we study when there is more

than one spatial dimension and in addition, spatial

data acts as measures within the fact table, these

spatial elements must be related among them to

some of spatial topological relations (spatial join)

described in Figure (2 a), (Figure 4).

Table 4: Spatial data Functions.

User Defined

Equi-partition, nearest-neighbor indexHolistic

Center of n geometric points, center of gravityAlgebraic

Convex hull, geometric union, geometric intersectionDistributive

User Defined

Equi-partition, nearest-neighbor indexHolistic

Center of n geometric points, center of gravityAlgebraic

Convex hull, geometric union, geometric intersectionDistributive

In the example 3, the spatial data is a measure within

the fact table and we want to study its evolution in

time from different granulaties, (Figure5).

We used the functions in (Table 2,1) as an

extension of Table 1 and Table 2. For the example,

we define a spatial object as a data type abstract

with an identity, a granularity, a geometry of

representation and a temporal granularity. The

granularity or unit of measure is associated to a

reference system. The geometry of representation is

associated to a dimension. We will utilize

geometries of two dimensions and the metric system

as reference. Although there are many more cases,

the size of this study prevents us from locking at all

of them.

5 JUSTIFYNG WE APPROACH

Example 1. We want to manage the collected

agricultural production of a set of plots through the

time. We wish to store the production as kilograms

of product gathered per semester in each plot. The

Plots have certain geography and we want to store

its area in meters and its changes for semester, as

well as the plot owner identified by the SSN. We

consider that the production of each plot is only one

product that does not vary in time, though the same

product can be simultaneously cultivated in several

plots.

We model this example with the extension of the

Snowflake scheme proposal (Figure 3). We have

three dimensions: Time Dimension, Owner

Dimension, and Plot Space Dimension; and a

Production fact table. The Time dimension is

established with three granularities: semester, year

and decade, and are represented in a hierarchy with

three levels, one for each granularity. Here, the

temporal dimension marks the time of changes of all

the dimensions. In the Plot dimension three

granularities are defined, Meter, Hectometer, and

Kilometer with three levels. The smaller granularity,

leaf level, represents spatial data with a geometry of

surface measured in meters; the second level

represents the spatial data with a lineal geometry

measured in hectometers; and the third level, the

data is represented with a point measured in

kilometers (Figure 2,a). The Owner dimension does

not have spatial data and it does not have any

hierarchy. The Production fact table has one

measure, KProd, which gathers the production of

each plot every semester; it also contains the keys of

leaf level of each dimension; the set of these keys

form the key of this fact table.

Production

KProd

IDP m

Sem_x

SSN

Year

Decade

Semester

Sem_x

Mr_thinning (IDP )

Ml_contr(IDP )

Plot Space Dimension

Static Hierarchy

Time Dimension

Dynamic Hierarchy

Owner Dimension

Plot m

IDP

Product

Sum (KPro )

Owner

SSN

…..

Production

KProd

IDP m

Sem_x

SSN

KProd

IDP m

Sem_x

SSN

Year

Decade

Semester

Sem_x

Mr_thinning (IDP )

Ml_contr(IDP )

Plot Space Dimension

Static Hierarchy

Time Dimension

Dynamic Hierarchy

Owner Dimension

KmKmKm

Plot m Plot m Plot m

IDP

Product

Sum (KPro )

Owner

SSN

…..

Owner

SSN

…..

Owner

SSN

…..

Figure 3: Example with one spatial dimension present in

the fact table.

We can see that the key of the Plot dimension is

spatial data, which contains an identity and a

geometry of surface associated with the unit metre.

Also, this key is propagated inside the fact table. As

we want to represent spatial data along with the

measure KProd.

The hierarchy of the Temporal dimension is a

dynamic hierarchy because it implies changes in the

measure of the fact table when navigating through

its levels. When doing Roll-up in the Time

dimension, i.e. we change the temporal granularity

from a smaller granularity to another more coarser

granularity, the aggregation function which we need

apply to Kprod measure the function Sum, the same

as for all levels. The hierarchy of the Plot spatial

dimension is an example of static hierarchy, because

KProd measure does not change when navigating

through its levels, however the spatial granularity of

plot spatial element changes. Thus, when making the

Roll-up from the leaf level to the second level of this

static hierarchy, the Mr_thinning function is applied

ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

178

(Table 2,1) on the plot spatial element, it is reduced

from a region (m) to a line (Hm), and when making

the Roll-up from the second level to the third level,

Ml_contr function is applied on the plot spatial

element, it is reduced from a line (Hm) to a point

(km).

Example 2. We want to represent the evolution

of the riverbeds and of the plots that cross a certain

geographic zone, through time. The updates are

made each month and we also want to study

geographic zones from the perspective of city, state

and country.

We show this example as Figure 4. We have

four dimensions: River Space, Plot Space, Location

and Time; and a fact table: Cross. In this scheme,

the topology functions are applied with two spatial

data, gathering the intersection or cross of two

different geometries, one for rivers and another for

surfaces of plots. The River Space Dimension has

two granularities, the less granularity (leaf level) is

represented with a lineal geometry show in metre

and the greatest granularity (second level) is show in

Hm unit associated to a point geometric. Plot Space

Dimension has three granularities, the less

granularity chosen is metre associated to a

polynomial representation, the second level has

hectometre unit associated to a geometric linear and

third level is represented as kilometre unit associated

to a geometric point. The Location dimension has

three levels: City, State and Country. The Time

dimension show by two granularities, month and

year, and has pre-established points in time. The

changes in the DW are made every month, and the

variations experienced by the different elements

present in the scheme, are only reflected at that time.

The Cross fact table has a measure that is the

intersection or crossing of the two spatial data, the

river spatial data and plot spatial data. The key of

this table is formed by the plot and river identities,

and also with the keys of the leaf levels of the

Location dimension and Time dimension.

In the Location dimension when Roll-up is

performed to reach a coarser granularity, the

aggregation function applied to the "intersection

(river, plot)" measure is the Union the same for all

levels. When Roll-up is done on the Time

dimension, in order to reach the coarser granularity

year, the M_last function, (Table 2,1) is applied to

“intersection (river, plot)” measure, and among all

the values of the spatial data of the granularity

months, we obtain at the end of every year. In the

River dimension to reach a coarse granularity from

the leaf level the Roll-up is applied and the Ml_contr

function is used on the river spatial attribute, which

reduces a line (m) to a point (Hm). In the Plot

dimension, the Roll-up applies the Mr_thinning or

Ml_contr function to the plot spatial attribute, which

reduces a region (m) to a line (Hm) or reduces a line

(Hm) to a point (km), respectively.

Each spatial element can change its granularity

independently of one another, and the intersection or

crossing between river spatial measure and plot

spatial measure can be performed through polygons

and lines, lines and points or across lines and lines, (

see Figure 4).

IDP m

IDR m

City_x

Month_x

City

State_x

Month

Month_x

Mr_thinning (IDP )

Ml_contr (IDP )

IDR

Ml_contr (IDR )

Location Dimension

Dynamic Hierarcy

Cross

State

Country

City_x

Country_x

Union (IDP,IDR )

Plot Space Dimension

Static Hierarchy

Time

Dimension

River m

IDP

M_Last (IDP, IDP )

Plot m

Year

Year_x

River Space Dimension

Static Hierarchy

Union ( IDP,IDR )

IDP m

IDR m

City_x

Month_x

City

State_x

Month

Month_x

Mr_thinning (IDP )

Ml_contr (IDP )

IDR

Ml_contr (IDR )

Location Dimension

Dynamic Hierarcy

Cross

State

Country

City_x

Country_x

Union (IDP,IDR )

Plot Space Dimension

Static Hierarchy

Time

Dimension

River m

IDP

M_Last (IDP, IDP )

Plot m

Year

Year_x

River Space Dimension

Static Hierarchy

Union ( IDP,IDR )

Figure 4: Example with more than one spatial dimension

present in the fact tables.

Example 3. We want study the evolution of the

plots whose variation is conditioned by the city to

which it belongs and by its owner, through time. We

want to store the plots as spatial data and its area

as numerical data. Also the timestamps included in

the DW will be motivated by the changes in

ownership and location of the plot, or in other

words, by events.

This example is modelled in Figure 5. In the fact

table we have two spatial measure focuses of study.

The Plot measure that gathers the evolution of the

plot through time and another Area measure, that

gathers the area of the plot in each evolution.

Although both of them are spatial data, the

characteristics and the treatment of them are differ;

Plot measure (represented by an identifier, a

geometry and a system of reference) and the Area

measure expressed in numerical form.

We believe that it is not necessary to have a spatial

dimension in order for a spatial measure to exist in

the fact table, nevertheless we propose that it be

included in the schema, when it is needed to treat

different granularities from a space object. Thus, we

introduce the Plot Space dimension associated to

Plot measure. Notice the intuitiveness of schema

when using the labels between the levels of

hierarchies to express the functions, applied to the

A MULTIDIMENSIONAL APPROACH TO THE REPRESENTATION OF THE SPATIO-TEMPORAL

MULTI-GRANULARITY

179

measures, when changing the granularities, i.e. when

the Roll-up is made, (Figure 5).

Evolution

IDP m

Area m

SSN

City_x

Time_x

State

Country

City

City_x

State_x

Country_x

Owner

SSN

Time

Time_x

Event_x

Union ( IDP )

Sum ( Area)

Union ( IDP )

Sum ( Area)

Mr_thinning (IDP )

Expre1(Area)

Ml_contr (IDP )

Expre2 (Area)

Plot Space Dimension

Static Hierarchy

Time

Dimension

Location Dimension

Dynamic Hierarcy

Owner Dimension

Plot m

IDP

Evolution

IDP m

Area m

SSN

City_x

Time_x

IDP m

Area m

SSN

City_x

Time_x

IDP m

Area m

SSN

City_x

Time_x

IDP m

Area m

SSN

City_x

Time_x

State

Country

City

City_x

State_x

Country_x

OwnerOwner

SSN

Time

Time_x

Event_x

Time

Time_x

Event_x

Time

Time_x

Event_x

Union ( IDP )

Sum ( Area)

Union ( IDP )

Sum ( Area)

Mr_thinning (IDP )

Expre1(Area)

Ml_contr (IDP )

Expre2 (Area)

Plot Space Dimension

Static Hierarchy

Time

Dimension

Location Dimension

Dynamic Hierarcy

Owner Dimension

KmKmKm

Plot m

IDP

Figure 5: Example with a spatial data like a measure in

the fact table and one related measure.

6 CONCLUSIONS

In this paper we have described a novel approach to

extend multidimensional logical model using an

extension of the Snowflake scheme. Our objective is

the treatment of spatio-temporal granularity in the

multidimensional model. We have studied the

behaviour of spatial data when is included in a

dimension or in fact tables. Moreover, we have

shown the changes of spatio-temporal granularity in

spatial data, within a scheme which is clear and

intuitive. The Temporal dimension is presented with

a point of time pre-established and like time points

produced by events. We propose a new class of

hierarchy, called Static hierarchy, within the spatial

dimensions to gather the different granularities in a

chosen spatial reference system. The treatment of

the Static hierarchy is different from the treatment of

the hierarchies used until now by traditional

multidimensional models. The navigation through

the different levels of this Static hierarchy does not

imply changes in the measures of the fact tables, nor

in the spatial attributes inherited from a spatial

dimension, present in the key of the fact table.

Nonetheless the navigation through Static hierarchy

implies changes in the spatial representation of

spatial element that appear in the fact table, allowing

its study from different persperctives. We also

propose to place a label between the consecutive

levels of the hierarchies, with information of name

of function and with the measure which uses the

function when Roll-up is made on the hierarchies.

This clarifies and increases the semantic

representation of the scheme. Our future work focus

on including spatial objects in the multidimensional

model from a conceptual perspective, taking

advantage of the expressiveness that this offers to

derive a conceptual sheme independent from the

platform, the study of spatial data in movement and

the study of new static hierarchies searching for

more applications.

REFERENCES

Bettini, C., Jajodia, S. & Wang, S. “Time Granularities in

Databases, Data Mining and Temporal Reasoning”.

Springer-Verlag, 2000.

Camossi, E. Bertolotto, M. Bertino, E. Guerrini, G. A

Multigranular Spactiotemporal Data Model, GIS ‘03’

Eisenberg, A., Melton, J., Kulkarni, K., Michels, J.E.,

Zemke, F. “SQL: 2003 Has Been Published”.

SIGMOD Record, vol. 33, no. 1, March 2004.

Ferri F. Porurabbas, E. Rafanelli, M. and Ricci, F..

Extending geographic databases for a query language

to support queries involving statistical data. In Proc.

Of the 8th ACM Symposium on Advances in

Geographic Information Systems, 2000

Forlizzi, L., Güting, R.H., Nardelli, E., Schneider, M. “A

data model and data structures formoving objects

database”. Proceedings of the 2000 ACM SIGMOD

International Conference on Management of data, pp:

319-330, 2000.

Han, J. Koperski, K. and Stefanovic, N. GeoMiner: A

system prototype for spatial data mining. In Proc. Of

the ACM SIGMOD Int. Conf. On Managemente of

Data, 1997

Kouba, Z. Matou¡sek, K. and Mik¡sovský, P. Novel

knowledge discovery tools in industrial applications.

In Proc. of the Workshop on Intelligent Methods for

Quality Improvement in Industrial Practice, pages

72-83, 2002.

Malinowski, E. and Zimányi, E. Representing Spatiality in

a Conceptual Multidimensional Model. GIS’04,

November 2004, Washington, DC, USA.

Miquel, M. Brisebois, A. Bédard, Y. and Edwards, G..

Implementation and evaluation of hypercube-based

method for spatio-temporal exploration and anlysis.

SCG661 2004

Pourabbas. Cooperation with geographic database. In

Rafanelli[25], pages 393-432.

Rives, S. Bédar, Y. and Marchand, P. Toward better

support for spatial decision making: Defining the

characteristics of spatial on- line analytical

processing (SOLAP). Geomatica, 55 (4), 2001

Stefanovic, N. Han, J. and Koperski, K. Object-based

selective materializacion for efficiente implementacion

of spatial data cubes. IEEE Trans. On Knowledge and

Data Engineering, 12(6):938-958, 2000.

ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

180