INTEGRATING FUZZY LOGIC IN ONTOLOGIES

Silvia Calegari and Davide Ciucci

Dipartimento di Informatica, Sistemistica e Comunicazione,

Universit

a degli Studi di Milano Bicocca,

via Bicocca degli Arcimboldi 8,

20126 Milano, Italy

Keywords:

Concept modiﬁers, fuzzy logics, fuzzy ontologies, membership modiﬁers, KAON, ontology editor.

Abstract:

Ontologies have proved to be very useful in sharing concepts across applications in an unambiguous way.

Nowadays, in ontology-based applications information is often vague and imprecise. This is a well-known

problem especially for semantics-based applications, such as e-commerce, knowledge management, web por-

tals, etc. In computer-aided reasoning, the predominant paradigm to manage vague knowledge is fuzzy set

theory. This paper presents an enrichment of classical computational ontologies with fuzzy logic to create

fuzzy ontologies. So, it is a step towards facing the nuances of natural languages with ontologies. Our pro-

posal is developed in the KAON ontology editor, that allows to handle ontology concepts in an high-level

environment.

1 INTRODUCTION

An ontology is a formal conceptualization of a partic-

ular domain of interest shared among heterogeneous

applications. It consists of entities, attributes, rela-

tionships and axioms to provide a common under-

standing of the real world (Lammari and Mtais, 2004;

Gruber, 1993; Guarino and Giaretta, 1995). With the

support of ontologies, users and systems can commu-

nicate with each other through an easier information

exchange and integration (Soo and Lin, 2001). On-

tologies help people and machines to communicate

concisely by supporting information exchange based

on semantics rather than just syntax.

There are ontological applications where informa-

tion is often vague and imprecise. For instance,

the semantic-based applications of the Semantic Web

(Berners-Lee et al., 2001), such as e-commerce,

knowledge management, web portals, etc. Indeed, the

conceptual formalism supported by a typical ontol-

ogy may not be sufﬁcient to represent uncertain infor-

mation that is commonly found in many application

domains. For example, keywords extracted by many

queries in the same domain may not be considered

with the same relevance, as some keywords may be

more signiﬁcant than others. Therefore, the need of

giving a different interpretation according to the con-

text emerges.

A possible solution to handle uncertain data and,

hence, to tackle these problems, is to incorporate

fuzzy logic into ontologies. The aim of fuzzy set

theory (Klir and Yuan, 1995) introduced by L. A.

Zadeh (Zadeh, 1965) is to describe vague concepts

through a generalized notion of set, according to

which an object may belong to a certain degree (typ-

ically a real number from the interval [0,1]) to a set.

For instance, the semantic content of a statement like

“Cabernet is a deep red acidic wine” might have de-

gree, or truth-value, of 0.6. Up to now, fuzzy sets and

ontologies are jointly used to resolve uncertain infor-

mation problems in various areas, for example, in text

retrieval (Bouquet et al., 2004; Singh et al., 2004; Ab-

ulaish and Dey, 2003) or to generate a scholarly on-

tology from a database in ESKIMO (Matheus, 2005)

and FOGA (Quan et al., 2004) frameworks. However,

in none of these examples there is a fusion of fuzzy set

theory with ontologies.

The aim of this paper is to present a proposal to di-

rectly integrate fuzzy logic in ontology in order to ob-

tain an extension of the ontology that is more suitable

for solving uncertainty reasoning problems. It is a

ﬁrst step towards the realization of a theoretical model

and of a complete framework based on ontologies that

are able to consider the nuances of natural languages.

In literature, a ﬁrst tentative has been made in the

context of medical document retrieval (Parry, 2004)

Calegari S. and Ciucci D. (2006).

INTEGRATING FUZZY LOGIC IN ONTOLOGIES.

In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 66-73

DOI: 10.5220/0002496100660073

 SciTePress

by adding a degree of membership to all terms in the

ontology to overcome the overloading problem. An-

other proposal is an extension of the domain ontology

with fuzzy concept (Chang-Shing et al., 2005), how-

ever only for Chinese news summarization.

This paper shows how to insert fuzzy logic during

ontology creation with KAON (KAON, 2005). This

software consists in a number of different modules

providing a broad range of functionalities centered

around creation, storage, retrieval, maintenance and

application of ontologies. KAON allows the use of

an ontology at high-level, and the relative conceptual

models are deﬁned in a natural and easily understand-

able way.

The rest of the paper is organized as follows: Sec-

tion 2 deﬁnes a fuzzy ontology and explains how to

deﬁne and use fuzzy values in it. Section 3 presents

the ontology editor used and it is shown how to in-

tegrate it with our framework. In Section 4, we give

an overview on related works and on the next steps of

our approach.

2 FUZZY LOGIC

In this section, we present a logical framework to sup-

port and to reason with uncertainty. This is a focus

aspect for all ontology-based applications where the

user is interested in information that often contains

imprecise and vague description of concepts. For ex-

ample, one may be interested in ﬁnding “a very strong

ﬂavored red wine” or in reasoning with concepts such

as “a cold place”, “an expensive item”, “a fast motor-

cycle”, etc.

In order to face these problems the proposed ap-

proach is based on fuzzy sets theory. It has not been

chosen a particular ontology domain to explain our

theory because our goal is to fulﬁl all nuances of nat-

ural languages and to take into account all the differ-

ent aspects that an ontology have to consider. Our

aim is to extend an ontology editor to directly handle

uncertainty during the ontology deﬁnition, so that to

enrich the knowledge domain.

At ﬁrst, let us remind the deﬁnition of a fuzzy set.

Let us consider a nonempty set of objects U, called

the universe.Afuzzy set or generalized characteris-

tic functional is deﬁned as a [0, 1]–valued function on

U, f : U → [0, 1]. Given an object x ∈ U , f (x)

represents the membership value of x to the set f .In

the following of this section we explain how to intro-

duce fuzzy values on different objects of an ontology

and how to automatically correct them. Finally, we

give some hint on the possible applications of a fuzzy

ontology.

2.1 Deﬁning a Fuzzy Value

The ﬁrst problem to tackle is how to assign a fuzzy

value to an entity of the ontology. The trade off is be-

tween understandability and precision, since (Casillas

et al., 2003)

to obtain high degree of interpretability and ac-

curacy is a contradictory purpose and, in prac-

tice, one of the two properties prevails over the

other one. Depending on what requirement is

mainly pursued, the Fuzzy Modelling ﬁeld may

be divided into two different areas:

1. Linguistic fuzzy modelling – The main objec-

tive is to obtain fuzzy models with a good in-

terpretability

2. Precise fuzzy modelling – The main objective

is to obtain fuzzy models with a good accu-

racy.

Since our goal is to be as general as possible, both

the possibilities are given to the expert: deﬁne a

precise value or a linguistic one. In the former

case the expert, while creating the ontology, de-

ﬁnes a function f :(Concepts ∪ Instance) ×

P roperties → Property

Value × [0, 1] with the

meaning that f (o, p) is the value that a concept or

an instance o assumes for property p with associated

degree. For example, in an hypothetical ontology of

cats, f(Garﬁeld,color) = (orange,0.8) means that for

the property color, the instance Garﬁeld, has value or-

ange with degree 0.8. Or, in a wine ontology, f(wine,

taste)= (full-bodied,0.4) means that the concept wine

has a full-bodied (the value) taste (the property) with

degree 0.4.

Clearly, there may exist situations in which no

property value is necessary for a given property.

For example, “Garﬁeld has sense of humour with

value 0.9” cannot be correctly expressed with the

just exposed formalism. In this situation, it is neces-

sary to map a pair (concept/instance, property) sim-

ply to [0, 1], i.e., f



:(Concept ∪ Instance) ×

P roperties → [0, 1] and the above example becomes



(Garﬁeld,sense of humour) = 0.9.

In order to simplify the nota-

tion, we can deﬁne a unique function

g :(Concepts ∪ Instances) × (P roperties ∪

Prop

val) → [0, 1]. Thus, “Garﬁeld has color

orange with value 0.8” becomes g(Garﬁeld,orange) =

0.8. Using these function g, the expert has the chance

to choose a membership value with inﬁnite accuracy,

that is precision is preferred to interpretability.

On the other hand, the second possibility is to

choose as membership value, a label in a given set.

We have chosen the set L ={little, enough, moder-

ately, quite, very, totally} which is clearly not exhaus-

tive of all the possible labels, but it can intuitively be

modiﬁed as desidered.

INTEGRATING FUZZY LOGIC IN ONTOLOGIES

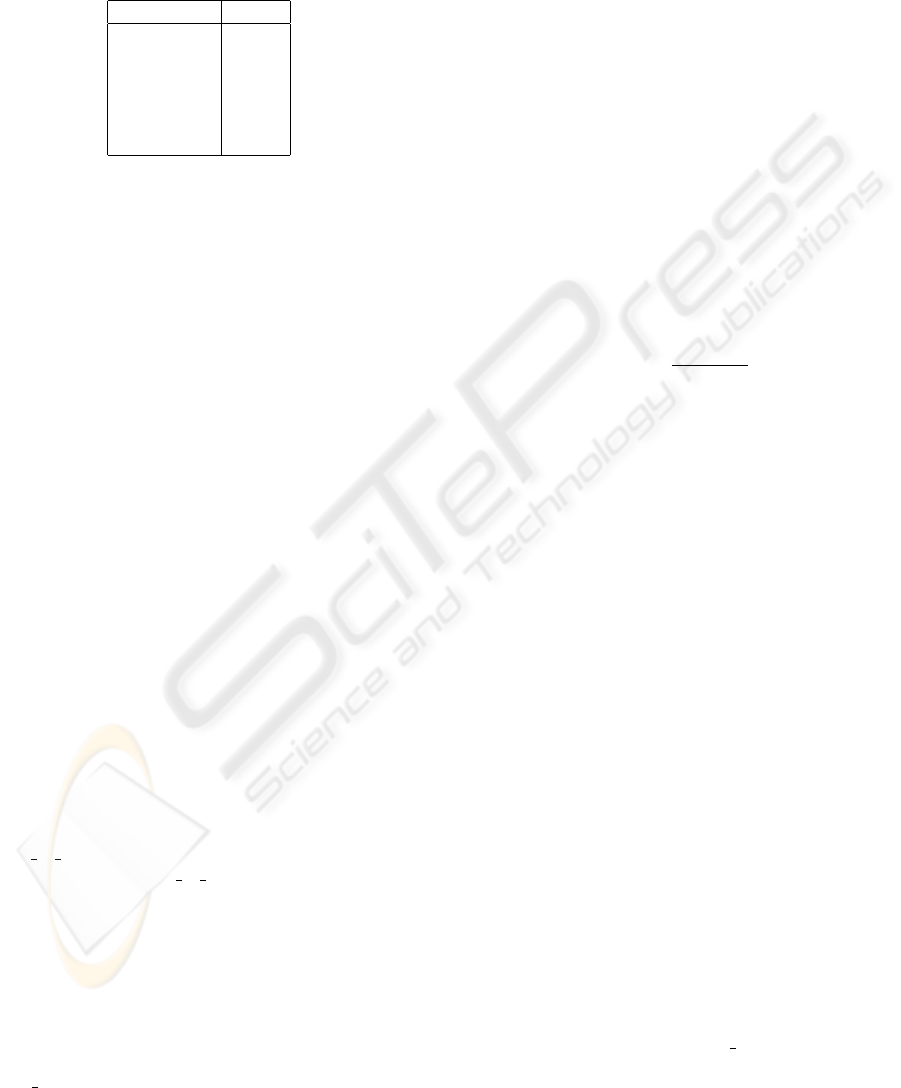
In this case the value g(o, p) is automatically as-

signed according to Table 1.

Table 1: assignement of fuzzy value to labels.

Label Value

little 0.2

enough 0.4

moderately 0.6

quite 0.7

very 0.8

totally 1

Summing up, we give the chance to add a mem-

bership value to a pair (concept/instance, property) in

two different ways: through a precise value v ∈ [0, 1]

or choosing a label in the predeﬁned set L. Thus,

through the function g we deﬁne a new relation in the

ontology domain.

Another possibility is to assign a fuzzy value to an

entity (concept or instance). This can be useful to

overcome the problem of overloading as outlined in

(Parry, 2004) and explained in Section 2.3. In this

case the expert can deﬁne a function h : Concepts ∪

Instances → [0, 1].

Let us remark that the fuzzy value assigned using

one of the two functions g and h is a number in the

unit interval [0, 1], that is, the usual support of a many

valued logic. Hence, applications based on fuzzy on-

tologies can use this value taking advantage of stan-

dard and well-studied tools. For instance, in order to

put together two (or more) different fuzzy values, an

aggregation operator (Calvo et al., 2002) can be used.

Typical examples are t–norm and t–conorms (Kle-

ment et al., 2000), that is, binary mappings which give

a semantic to the “OR”, “AND” operators. The most

known are G

odel norm and conorm, i.e., the min–max

operators. Considering the above example, it may be

necessary to compute the truth value of the statement

“Garﬁeld is orange AND has sense of humour”. If it

is known that f(Garﬁeld,orange)=0.8 and f(Garﬁeld,

sense

of humour) = 0.9 then [f(Garﬁeld,orange)

AND f (Garﬁeld, sense

of humour)] = min{0.8,0.9}

= 0.8.

Finally, we can give the deﬁnition of fuzzy ontol-

ogy.

Deﬁnition 1. A fuzzy ontology is an ontology ex-

tended with fuzzy values which are assigned through

the two functions

g :(Concepts ∪ Instances) × (P roperties ∪

Prop

val) → [0, 1] and

h : Concepts ∪ Instances → [0, 1].

2.2 Updating a Fuzzy Value

Once an expert has created a fuzzy ontology, it is not

realistic to assume that it is perfect and that any fuzzy

value is well-deﬁned and suited to any environment.

Thus, a mechanism to change fuzzy values in order to

ﬁt them in the best way to a speciﬁc environment or, in

general, to make them more correct is needed. Here,

we propose a method to update fuzzy values accord-

ing to results of some queries on some documents. We

do not enter into details about how syntactically spec-

ify queries, but we assume that we are able to perform

them and that their results are available to us.

Let us suppose that the current fuzzy value is f and

as a result of a query it must be updated to f

new

. The

simpliest possibility is to set f := f

new

. However,

it is reasonable to suppose that after some queries the

fuzzy property has reached a stable value, hence it is

not useful to change it with f

new

, losing all the his-

tory of the acquired knowledge. A solution can be to

diminish the importance of f

new

at any change:

f := f +

new

− f

Q +1

(1)

where Q is the number of updates perfomed for that

value. Clearly, the value Q must be stored in the on-

tology for any deﬁned fuzzy value.

Now, the issue is how to compute a new fuzzy

value f

new

. It is unlikely to ﬁnd in a document a

precise deﬁnition of a fuzzy value, but usually a lin-

guistic qualiﬁer can be found. For example, we do

not ﬁnd “Cabernet has a dry taste with value 0.6”, but

it make sense a document such “Cabernet has a very

dry taste”. So a method to make use of this kind of

information is needed. Here we propose an approach

based on concept modiﬁers (Zadeh, 1972).

A concept modiﬁer has the effect to alter the fuzzy

value of a property. Given a set of linguistic hedges

such as “very”, “more or less”, “slighty”, a concept

modiﬁer is a chain of one or more hedges, such as

“very slightly” or “very very slightly”. To any (lin-

guistic) concept modiﬁer it is necessary to associate a

(numerical) membership modiﬁer.

Deﬁnition 2. A membership modiﬁer is a value β>0

which is used as an exponent to modify the value of a

membership function f as f

According to their effect on a fuzzy value, a hedge

can be classiﬁed in two groups: concentration type

and dilation type. The effect of a concentration mod-

iﬁer is to reduce the grade of a membership value.

Thus, in this case, it must be β>1. For instance, to

the hedge “very”, it is usually assigned β =2. So,

if we know that g(Cabernet, dry

taste)=0.8, i.e.,

“Cabernet has a dry taste with value 0.8”, then Caber-

net has a very dry taste with value 0.8

=0.64.On

the contrary a dilation hedge has the effect to raise a

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

membership value, that is β ∈ (0, 1). For instance,

if to slightly it is assigned β =0.25 and g(Cabernet,

dry

taste)=0.8, then Cabernet has a slightly dry taste

with value 0.8

0.25

=0.95 according to the intu-

ition that if something is “dry” then it is even more

“slightly dry”. Let us remark that this approach is dif-

ferent from the original Zadeh’s one (Zadeh, 1972),

where “slightly”, as well as other modiﬁers, is han-

dled in a more complicated manner. This method has

the advantage to give a uniform and simply way to

manage concept modiﬁers, even if, a deeper study

about the semantic of this way of handling chain of

modiﬁers is needed.

So, a concept modiﬁer is used in literature to de-

ﬁne a new fuzzy membership given an already exist-

ing one. For example, if we know the fuzzy value of

property red we can infer the fuzzy membership of

property very red simply by raising to the power 2 the

value of red (see the above examples). However, here

we are in the opposite situation. As an example, let us

suppose to know, from an ontology, the red property

and also, as a result of a query, that a certain object

is “very red”. Hence, from very red we need to in-

fer a new red property (before “red” was ﬁxed, here

it changes) for that object and clearly if an object is

very red it is even more red. So, if in the ontology

g(o, red)=0.7, we must increase this value, for ex-

ample g(o, red)=0.7

0.5

. In conclusion, the effect of

very is to raise the value of the property it is referred

to and not to reduce its magnitude. In a schematic

way, it is possible to say that in the usual case it is

performed the deduction

red → very red

whereas in this situation:

red and very red → red

This argument also applies to all the other concept

modiﬁers. Thus, in our case what is usually consid-

ered as a concentration modiﬁer becomes a dilation

one and vice versa.

Two issues need now to be faced: decide which

modiﬁers we consider (and which are their values)

and deﬁne a method to compute β values for chains

of concept modiﬁers.

About the former problem, the chosen set of hedges

is H ={very, much more, more, more or less, moder-

ate, slightly}. This is only one of the possible choices.

The set H can be changed according to one

s needs, on

condition that it satisﬁes the following two properties.

• The set H is totally ordered, i.e., very < ... <

slightly and only the β value for the smaller and

greater elements are ﬁxed, respectively as 0.5 and

• The two subsets of contraction hedges {more or

less, moderate, slightly} and dilation hedges {very,

much more, more} have the same cardinality.

These two conditions are due to the fact that we pro-

pose to adopt the algorithm presented in (Khang et al.,

2002) in order to compute the membership modiﬁer

of a sequence of hedges. The only difference is the

order inversion of the hedges, this is due to the use we

are doing of concept modiﬁers which is, as explained

above, opposite to the original approach.

Moreover, we consider also the further modiﬁer

not which behaves as the standard involutive nega-

tion on fuzzy sets: not(x):=1− x.Asanex-

ample let us suppose that g(Cabernet,dry

taste)=0.8,

then if in a document it is found that “Cabernet has

not a dry taste” the new value is g

new

(Cabernet,

dry

taste) =1− 0.8=0.2. This way of han-

dling the not connective cannot be easily applied to

chains of hedges. Using the same example, if we

ﬁnd that “Cabernet has not a very dry taste”, the new

value is g

new

(Cabernet, dry taste)=1−

√

0.8=

0.11. However, “not very dry ” induces to think to

something which is dry but not at an high degree

and this is not correctly mirrored by g

new

(Cabernet,

dry

taste)=0.11. In (Singh et al., 2004) a solution to

integrate not in the set H of all concept modiﬁers is

presented. This solution does not seem to us a good

one, since it cannot be applied directly to a property,

but only to another concept modiﬁer and also in this

case it can generate a negative β if the original algo-

rithm of (Khang et al., 2002) is not modiﬁed. Thus,

handling chains of modiﬁers which include not is left

as an open problem. Pacholczyk et al. dedicated sev-

eral works to the problem of linguistic negation (see

for instance (Pacholczyk, 1998; Pacholczyk et al.,

2002)). So an interesting future work would be the

integration of those studies in our approach.

Another open problem is that the set H of concept

modiﬁers is certainly not exhaustive of all the nuances

of natural language. Lots of elements could be added

to H and this will require new algorithms to handle it,

since not all existing concept modiﬁers can be totally

ordered or exactly split into two subgroups of same

cardinality.

2.3 Examples of Application

In this section we give two examples of a possible use

of fuzzy ontologies. The ﬁrst one is based on fuzzy

values associated to (instance, properties) pairs and

the second one is a way to use concepts with fuzzy

values to remedy the overloading problem.

Extending queries When performing a query on a

document, it is a usual practice to extend the set of

concepts already present in the query with other ones

which can be derived from an ontology. Tipically,

given a concept, also its parents and children can be

added to the query and then searched in the document.

INTEGRATING FUZZY LOGIC IN ONTOLOGIES

A possible use of fuzzy ontology is to extend

queries with, besides children and parents, instances

of concepts which satisﬁes to a certain degree the

query. Let us explain it with an example. We are given

a clothes ontology and a query looking for “a very

long and black coat”. In the ontology there are two

instances of coat: X which has property “long” with

value 0.7 and Y which has property “long” with value

0.3. Thus, it is natural to extend the original query

adding, not only parents and children of the concept

“coat”, but also the instance X, because “long =0.7”

can be interpreted as “very long”. On the other hand,

the instance Y is not added to the extended query

since “long =0.3” does not mean “very long”.

To make a choice on which instances have to be

added to the extended query, we have to decide how

linguistic labels are mapped to numerical values. The

solution is again as in Section 2.1, that is only label

belonging to set L are admitted in queries and they

are mapped to numerical values according to Table 1.

If c is a concept, p is a property and l a label then

µ(c, p, l) is the value given to the label l for property

p and concept c. For instance in the above example,

the property “a very long coat” is translated to µ(coat,

long, very) =0.8. Now, we consider all the instances

i of the concept c and they are included in the ex-

tended query if and only if :

|µ(c, p, l) − g(i, p)|≤ (2)

where  ∈ [0, 1] is a level of tolerance. Obviously,

the number of instances to be added to the extended

query depends on the value of , the greater is 

the

most are the instances. The boundary cases are  =0,

only the instances that exactly match the query are

included, and  =1, all the instances are included.

Coming back to the example, if we ﬁx  =0.2, then,

|µ(coat, long, very) − g(X, long)| =0.8 − 0.7=

0.1 ≤ 0.2=, whereas |µ(coat, long, very) −

g(Y, long)| =0.8 − 0.3=0.5 ≥ 0.2=. Hence, X

is included in the extended query and Y is not.

Clearly, this is the simplest case where only one

property is present in the query. If two or more request

must be satisﬁed, a generalization of equation (2) is

needed. Let us suppose that in the query there are

n properties referred to the same concept c, then in-

stance i is considered iff



j=1

|µ(c, p

) − g(i, p

≤  (3)

That is we require that the mean value of the distances

between the values of the properties in the query and

the values of the properties in the instance is less than

the tolerance .

Overloading of concepts As anticipated in Sec-

tion 2.1 a possible use of the fuzzy value associated to

concepts is to limit the problems due to overloading

of a concept in an ontology. The solution we are go-

ing to expose has been proposed in (Parry, 2004). In

our opinion this approach is more related to statistics

than to fuzzy logic, nevertheless it can be managed by

our fuzzy ontology.

Let us suppose that a concept c is present in dif-

ferent parts of the ontology, the aim is to give an in-

dication about which place is more signiﬁcant with

respect to a certain domain. At a ﬁrst stage, to any

concept which is present in multiple locations is given

an equal fuzzy value such that they sum up to 1. For

instance, if c is present in 4 places, respectively de-

noted as c

then we have h(c

)=0.25. For any c

the set of its local terms L

, i.e., parents and children

in the ontology, is computed. Then, all the elements

l ∈ L

are searched in the documents under analysis

and a weight w

is assigned to them according to the

relevance they have in the document. Let us suppose

that in the document under investigation, there are l

occurencies for the element l. Then, for any concept

and for any document d the following function is

computed:

):=



(4)

The sum over all n documents of µ

is denoted as µ:

µ(c

):=



d=1

. Then, the new membership value

for concept c

and document d is:

new

):=

)

µ(c

)

(5)

These values are then used to update h(c

) according

to Equation 1 and they are applied in order of rele-

vance, so that a value due to a more relevant docu-

ment is applied ﬁrst and it has a greater inﬂuence than

the following ones.

3 HOW TO USE KAON

The KAON project is a meta-project carried out at the

Institute AIFB, University of Karlsruhe and at the Re-

search Center for Information Technologies (FZI).

KAON includes a comprehensive tool suite allow-

ing easy creation, maintenance and management of

ontologies. Furthermore, it provides a framework for

building ontology-based applications. An important

user-level application supplied by KAON is an on-

tology editor called OI-modeler. It allows to handle

entities of an ontology in a natural way. The most im-

portant features of the OI-modeler are its support for

manipulation of large ontologies and the support for

user-directed evolution of ontologies. Ontologies can

be simultaneously edited by multiple users (AA.VV.,

2004). The ontology navigation is more easy through

graph-based and tree-based metaphors.

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

In the last years, KAON has been used in many

areas like e-commerce and b2b applications (Motik

et al., 2002), autonomic and self-healing, self-

conﬁguring computational system (Stojanovic et al.,

2004) and more recently, it has been applied to the Se-

mantic Web (Bozsak et al., 2002; Oberle et al., 2005).

Root

Winery

Meal Course

Wine Grape

Wine Region

Consumable Thing

Food

Drink

Wine

body

color

flavor

grape

maker

name

sugar

full, medium, light

red, rosate, white

delicate, moderate, strong

dry, sweet, off−dry

Legend:

Concept

Subconcept

instance

property

property value

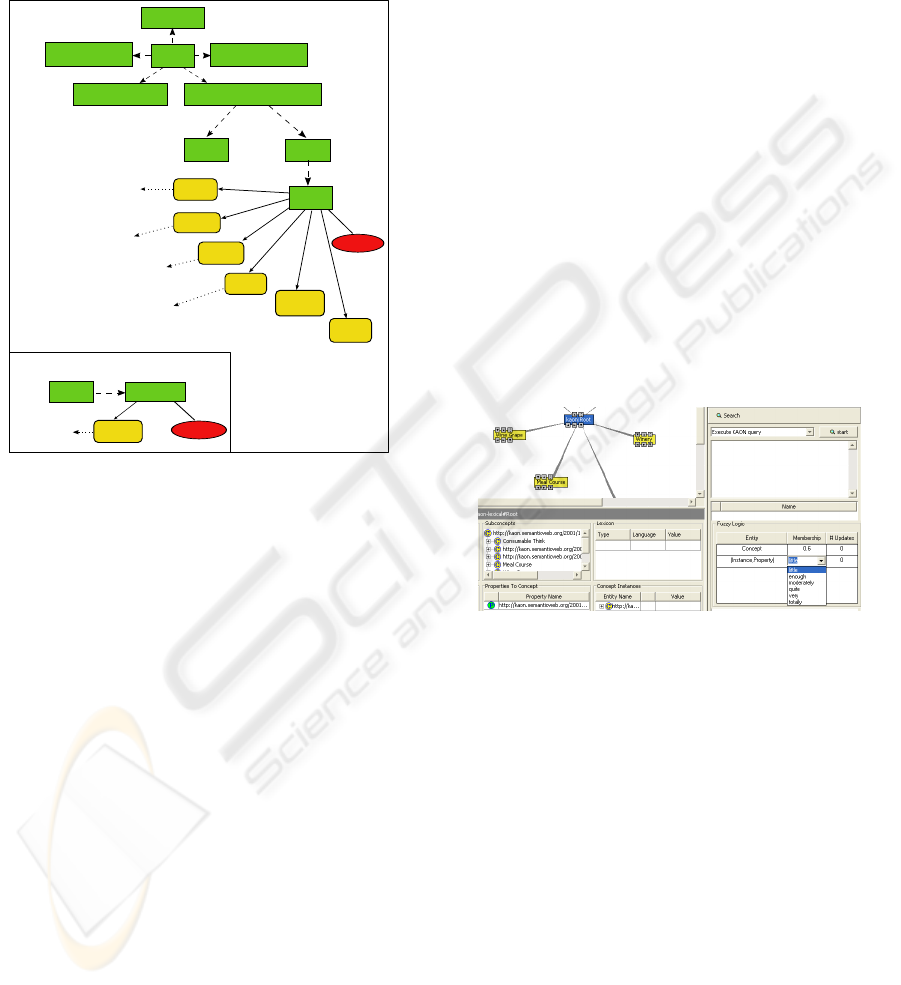
Figure 1: Wine ontology.

3.1 Ontologies in KAON

An ontology in KAON consists of concepts (sets of

elements), properties (speciﬁcations of how objects

may be connected) and instances grouped in reusable

units called OI-models (ontology-instance models)

(AA.VV., 2004). The conceptual model proposed al-

lows to deﬁne an entity in different ways, depend-

ing on the point of view of the observer. That is,

an entity can be interpreted as a concept, as well as

an instance. Moreover, property instantiation must be

in accordance with the domain and range constraints

(i.e. axioms, general rules, value-allowed) and must

obey the cardinality constraints, as speciﬁed by the

property speciﬁcations. An OI-model may include

other OI-models, and have immediate access to all de-

ﬁnitions from the included model.

Figure 1 is an example of an ontology in KAON:

it represents only a partial ontology deﬁnition about

wine. We have chosen such ontology because it is

largely widespread and known, and so it is more

simply to understand the reasoning approach used in

KAON.

In KAON language, it is possible to deﬁne well-

known symmetric, transitive and inverse proper-

ties, with the addition of modularization and meta-

modeling (AA.VV., 2004). Obviously, each of these

features allow to manage two types of implicit knowl-

edge: axioms and general rules. The formers are a

standard set of rules, such as the transitive properties,

the latters are general rules to combine and to adapt

information deﬁned in an ontology domain.

Moreover, KAON language allows to specify so-

called lexical entries (i.e. labels, synonyms, stems, or

textual documentation) which reﬂect various nuances

of natural languages. For example, the same lexical

entry may be associated with several elements: the

label BEAR may be associated with an instance rep-

resenting a bear as an animal or as a puppet. Further-

more, the instances can be deﬁned in different lan-

guages, namely English, German, French, Spanish,

Portuguese, Arabic and Chinese.

3.2 Fuzzy Ontologies in KAON

Our aim is to enrich KAON language adding the pro-

posed fuzzy-sets approach. In the following, it is

showed how we have integrated our framework in the

KAON project.

Figure 2: New KAON ontology overview.

Figure 2 represents a “Fuzzy Inspector” developed

to create in KAON the fuzzy ontology. The new panel

has been called “Fuzzy Logic” (see right lower corner

in Figure 2) and it allows the expert an easy fuzzy

logic integration. The Fuzzy Inspector is composed

by a table representing fuzzy entity, membership de-

gree and number of updates Q.

The domain expert can choose his fuzzy entity

(concept or instance) simply clicking up through two

types of interface proposed by KAON, namely graph-

based and tree-based metaphors, partially showed in

the screenshot. Moreover, the expert can select the

link between an instance and a property adding its

fuzzy value.

Thus, the expert can create real fuzzy ontology do-

main selecting the entity and directly inserting fuzzy

logic through the Fuzzy Inspector Panel purposely de-

veloped. In Figure 2, we propose two ways to use the

Fuzzy Logic Panel. In the ﬁrst row the expert types

INTEGRATING FUZZY LOGIC IN ONTOLOGIES

the membership degree according to his point of view.

In the second row he can choose the apposite value by

a list. The selected element in the list will be referred

to an a-priori deﬁned numerical value as explained in

Section 2.1. In the deﬁnition phase of the ontology

the number of the updates is zero. This value will

be changed during the queries in accordance with the

functions deﬁned in previous sections.

KAON’s ontology language is based on RDFS

(RDFS, 2004) with proprietary extensions for al-

gebraic property characteristics (symmetric, transi-

tive and inverse), cardinality, modularization, meta-

modelling and explicit representation of lexical infor-

mation.

In literature, all the limits about the RDFS are

well-known. Thus, it has been developed KAON2

(KAON2, 2005) that is a successor of the KAON

project. The main difference as to previous KAON

version is the supported ontology language, namely

KAON used a proprietary extension of RDFS,

whereas KAON2 is based on OWL DL (OWL, 2005).

OWL DL is a sublanguage of OWL (OWL, 2005)

and it supports those users who want the maximum

expressiveness without losing computational com-

pleteness (all conclusions are guaranteed to be com-

puted) and decidability of reasoning systems (all com-

putations will ﬁnish in ﬁnite time).

In more details, KAON2’s language is based on a

combination of the OWL DL and OWL Lite sublan-

guages (KAON2, 2005) of the OWL Web Ontology

Language (OWL, 2005).

Recently, some proposals to integrate fuzzy logic

in OWL have been presented (Straccia, 2005; Stoilos

et al., 2005; Pan et al., 2005).

The more complete and suitable to our study

seems to be the extension of SHOIN (D) presented

in (Straccia, 2005).

Thus, the next and last step to the integration of

fuzzy ontology in KAON2 is a deeper analysis of all

these approaches and the adaptation of one of them to

our situation. This is out of the scope of the present

paper and will be proposed in a forthcoming work.

4 CONCLUSION

In this paper, we have introduced fuzzy logic directly

in the ontology during the domain deﬁnition, enrich-

ing the actual features proposed by other ontology ed-

itors. The proposed solution allows to represent and

to reason with uncertain information. This is a deli-

cate problem for all those areas where the applications

are based on ontology.

The domain expert has two possibilities to add a

membership value in an ontology domain: through a

pair ({concept,instance},property) or through an en-

tity {concept, instance}. In both solutions, he/she can

assign this degree through a precise value v ∈ [0, 1]

or choosing a label in the predeﬁned set L.

We have also proposed a method, based on con-

cept modiﬁers, to automatically update the member-

ship degree during queries, useful, as example, for the

extraction of more relevant documents.

Furthermore, we have presented two possible ex-

amples of application: to extend a query and to over-

come the problem of overloading.

KAON has been the ontology editor chosen to in-

troduce fuzzy logic during the ontology deﬁnition.

We have integrated fuzzy logic in KAON, developing

a suitable Fuzzy Inspector Panel.

In the future, it is necessary to develop fuzzy-OWL

in KAON2 and to test all the proposed framework.

Furthermore, we plan to enrich our theory considering

linguistic negation. This is another crucial topic in

order to handle all the uncertainty situations proposed

by natural languages within the ontological domain.

REFERENCES

AA.VV. (2004). Developer’s Guide for KAON 1.2.7. Tech-

nical report, FZI Research Center for Information and

WBS Knowledge Management Group.

Abulaish, M. and Dey, L. (2003). Ontology Based Fuzzy

Deductive System to Handle Imprecise Knowledge.

In In Proceedings of the 4th International Conference

on Intelligent Technologies (InTech 2003), pages 271–

278.

Berners-Lee, T., Hendler, T., and Lassila, J. (2001). The

semantic web. Scientiﬁc American, 284:34–43.

Bouquet, P., Euzenat, J., Franconi, E., Seraﬁni, L., Stamou,

G., and Tessaris, S. (2004). Speciﬁcation of a common

framework for characterizing alignment. IST Knowl-

edge web NoE, 2.2.1.

Bozsak, E., Ehrig, M., Handschuh, S., Hotho, A., Maedche,

A., Motik, B., Oberle, D., Schmitz, C., Staab, S., Sto-

janovic, L., Stojanovic, N., Studer, R., Stumme, G.,

Sure, Y., Tane, J., Volz, R., and Zacharias, V. (2002).

KAON - Towards a large scale Semantic Web. In E-

Commerce and Web Technologies, Third International

Conference, EC-Web 2002, proceedings, volume 2455

of LNCS, pages 304–313. Springer-Verlag.

Calvo, T., Mayor, G., and Mesiar, R., editors (2002). Ag-

gregation Operators. Physica–Verlag, Heidelberg.

Casillas, J., Cordon, O., Herrera, F., and Magdalena, L.

(2003). Accuracy improvements to ﬁnd the balance

interpretability–accuracy in linguistic fuzzy model-

ing:an overview. In Accuracy Improvements in Lin-

guistic Fuzzy Modeling, pages 3–24. Physica-Verlag,

Heidelberg.

Chang-Shing, L., Zhi-Wei, J., and Lin-Kai, H. (2005). A

fuzzy ontology and its application to news summa-

ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

rization. IEEE Transactions on Systems, Man, and

Cybernetics-Part B: Cybernetics, 35:859–880.

Gruber, T. (1993). A Translation Approach to Portable On-

tology Speciﬁcations. Knowledge Acquisition, 5:199–

220.

Guarino, N. and Giaretta, P. (1995). Ontologies and Knowl-

edge Bases: Towards a Terminological Clariﬁcation.

In Mars, N., editor, Towards Very Large Knowledge

Bases: Knowledge Building and Knowledge Sharing,

pages 25–32. IOS Press, Amsterdam.

KAON (2005). Karlsruhe Ontology and Semantic Web

Tool Suite (KAON). http://kaon.semanticweb.org.

KAON2 (2005). Karlsruhe Ontology and Se-

mantic Web Tool Suite 2 (KAON2).

http://kaon2.semanticweb.org.

Khang, T. D., St

orr, H., and H

olldobler, S. (2002). A

fuzzy description logic with hedges as concept modi-

ﬁers. In Third International Conference on Intelligent

Technologies and Third Vietnam-Japan Symposium on

Fuzzy Systems and Applications, pages 25–34.

Klement, E. P., Mesiar, R., and Pap, E. (2000). Triangular

Norms. Kluwer Academic, Dordrecht.

Klir, G. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic:

Theory and Applications. Prentice Hall.

Lammari, N. and Mtais, E. (2004). Building and maintain-

ing ontologies: a set of algorithms. Data and Knowl-

edge Engineering, 48:155–176.

Matheus, C. (2005). Using Ontology-based Rules for Situ-

ation Awareness and Information Fusion. In Position

Paper presented at the W3C Workshop on Rule Lan-

guages for Interoperability.

Motik, B., Maedche, A., and Volz, R. (2002). A Conceptual

Modeling Approach for Semantics-Driven Enterprise

Applications. In Proceedings of the First Interna-

tional Conference on Ontologies, Databases and Ap-

plication of Semantics (ODBASE-2002), volume 2519

of LNCS, pages 1082–1099. Springer-Verlag.

Oberle, D., Staab, S., Studer, R., and Volz, R. (2005). Sup-

porting application development in the semantic web.

ACM Trans. Inter. Tech., 5:328–358.

OWL (2005). Ontology Web Language (OWL).

http://www.w3.org/2004/OWL/.

Pacholczyk, D. (1998). A new approach to linguistic

negation based upon compatibility level and tolerance

threshold. In Polkowski, L. and Skowron, A., edi-

tors, Proceedings of RSCTC98, volume 1424 of LNAI,

pages 416–423.

Pacholczyk, D., Quafafou, M., and Garcia, L. (2002). Opti-

mistic vs. pessimistic interpretation of linguistic nega-

tion. In Proceedings of AIMSA02, volume 2443 of

LNAI, pages 132–141.

Pan, J., Stamou, G., Tzouvaras, V., and Horrocks, I. (2005).

f-swrl: A Fuzzy Extension of SWRL. In ICANN 2005,

volume 3697 of LNCS, pages 829–834. Springer-

Verlag.

Parry, D. (2004). A fuzzy ontology for medical document

retrieval. In Proceedings of The Australian Workshop

on DataMining and Web Intelligence (DMWI2004),

pages 121–126, Dunedin.

Quan, T., Hui, S., and Cao, T. (2004). FOGA: A Fuzzy On-

tology Generation Framework for Scholarly Semantic

Web. In Knowledge Discovery and Ontologies (KDO-

2004). Workshop at ECML/PKDD.

RDFS (2004). Resource Description Framework Schema

(RDFS). http://www.w3.org/TR/PR-rdf-schema.

Singh, S., Dey, L., and Abulaish, M. (2004). A Framework

for Extending Fuzzy Description Logic to Ontology

based Document Processing. In Proceedings of AWIC

2004, volume 3034 of LNAI

, pages 95–104. Springer-

Verlag.

Soo, V. W. and Lin, C. Y. (2001). Ontology-based infor-

mation retrieval in a multi-agent system for digital li-

brary. In 6th Conference on Artiﬁcial Intelligence and

Applications, pages 241–246.

Stoilos, G., Stamou, G., Tzouvaras, V., Pan, J. Z., and Hor-

rocks, I. (2005). Fuzzy OWL: Uncertainty and the

Semantic Web. In International Workshop of OWL:

Experiences and Directions (OWL-ED2005), Galway,

Ireland.

Stojanovic, L., Schneider, J., Maedche, A., Libischer, S.,

Studer, R., Lumpp, T., Abecker, A., Breiter, G., and

Dinger, J. (2004). The role of ontologies in autonomic

computing systems. IBM Systems Journal, 43:598–

616.

Straccia, U. (2005). Towards a Fuzzy Description Logic

for the Semantic Web Preliminary Report. In

ESWC 2005, volume 3532 of LNCS, pages 167–181.

Springer-Verlag.

Zadeh, L. A. (1965). Fuzzy sets. Inform. and Control,

8:338–353.

Zadeh, L. A. (1972). A fuzzy-set-theoretic interpretation of

linguistic hedges. Journal of Cybernetics, 2:4–34.

INTEGRATING FUZZY LOGIC IN ONTOLOGIES