VECTOR BASED MAPPING OF POLYGONS ON IRREGULAR

TERRAIN MESHES FOR WEB 3D MAP SERVICES

Arne Schilling, Jens Basanow and Alexander Zipf

i3mainz - Institute for Spatial Information and Surveying Technology, University of Applied Sciences FH Mainz

Holzstraße 36, Mainz, Germany

Keywords: Cartography, Geographical Information Systems, computational geometry, 3D landscape models.

Abstract: In this paper we show how to efficiently integrate traditional GIS data into terrain models in order to

generate complete 3D maps with little overhead for textures. The results meet the requirements for the Web

3D Service (W3DS), a proposal for the standardization for delivering 3D web maps. Our approach is

designed to create fully vectorized 3D scenes that deliver the best possible quality and do not require

dynamic texture generation and handling. We describe the mesh operations for integrating polygonal GIS

data like forests, parks, buildings blocks, or streets into the terrain mesh and compare the results with a

texture based approach.

1 INTRODUCTION

In recent years much effort has been invested into

the standardization of 3D GIS (Geographical

Information Systems) solutions and to make them

suitable for web applications. The Open Geospatial

Consortium (OGC) plays a major role in this

standardization process and has already issued a

range of specifications for GIS web services, e.g. a

Web Map Service (WMS) or Web Feature Service

(WFS). Currently the foundations for exchanging 3D

GIS related data structures and graphics over

internet protocols are being discussed and first

solutions implemented. The new specifications and

recommendations include a Web 3D Service (W3DS

- OGC 2005) which delivers 3D map display

elements that can be explored in real time by any

web client, and an information rich data exchange

model (CityGML - Kolbe et al. 2005) that is

specifically designed for 3D city models. The latter

incorporates not only the geometrical description but

also semantic information of typical GIS objects.

In order to make a 3D Spatial Data Infrastructure

(SDI) work, which is the eventual goal of our

activities, it is not sufficient to agree on the technical

interfaces. A major research topic is related to the

integration and preparation of various data coming

from different sources. This refers to the automatic

assembly of different Levels of Detail (LODs),

integration of official cadastre data (Stoter 2004),

terrain-object integration, point object processing,

and other problems. In Schilling and Zipf (2002) the

authors showed how to apply such integrated

visualization models for 3D tour animations.

In this paper we focus on the integration of

traditional 2D GIS data into 3D landscape and city

models which use terrain models as basic height

source. Such models may be referred to as 2,5D, but

can be complemented with models coming from 3D

databases. The 2D data comes typically from a WFS

and must be mapped on the terrain model based on

Triangulated Irregular Networks (TIN).

The remainder of this paper is structured as

follows. First, we compare different approaches for

the integration of 2D GIS data and digital elevation

models. Then we briefly explain the technical

background and requirements before we go into

detail about the geometrical operations of our

approach. In the last section we compare our results

with an image based overlay.

198

Schilling A., Basanow J. and Zipf A. (2007).

VECTOR BASED MAPPING OF POLYGONS ON IRREGULAR TERRAIN MESHES FOR WEB 3D MAP SERVICES.

In Proceedings of the Third International Conference on Web Information Systems and Technologies - Web Interfaces and Applications, pages 198-205

DOI: 10.5220/0001274201980205

 SciTePress

2 RELATED WORK

We can distinguish 2 general approaches how to

display 2D vector data together with surface models.

1) The most common approach is to render

vector graphics into an image and to project it on the

terrain as texture. Traditional GIS layers, raster data,

and sometimes scanned paper maps are overlaid and

combined to a single texture layer (e.g. Haeberling

1999). Additionally, hardware accelerated

techniques like mip-map filtering and image

pyramids can be used to optimize rendering speed

and memory consumption.

In contrast to this static method also a dynamic

version has been investigated by Kersting and

Döllner 2002. They extend the concept of static

texture pyramids and introduce on-demand texture

pyramids, which are not prepared in a pre-

processing step, but rendered for each frame using

an off-screen pixel buffer (p-buffer, see also Wynn

2001). The advantage of this method is that huge

amounts of texture data that would be necessary for

every possible resolution don’t need to be

transmitted over the network. Instead, only the 2D

vector data is being transmitted. Since the p-buffer is

hardware accelerated, the images of the texture

pyramids can be rendered on demand for arbitrary

resolutions.

2) The second approach is a geometry based

mapping, i.e. to adapt the 2D vector data to the

surface of the terrain model and to render it as

separate geometric primitives.

Wartell et al. 2003 show how to overlay 2D

polylines on top of terrain models. The overlayed

polylines are rendered independently from other

image data due to rasterization artefacts. They

present the triangle clipping DAG (direct acyclic

graph) data structure which allows rendering the

projected polylines together with a quad-tree based

terrain model. They address the challenging problem

of combining progressive terrain meshes, which

change at nearly every frame as described by e.g.

Hoppe 1998 or Lindstrom and Pascucci 2002, with

3D polyline data, which also needs to adapt

accordingly.

Agrawal et al. 2006 use a similar technique for

combining a textured terrain model with polyline

data. In their case, the terrain is organized as block-

based LOD structure derived from a height raster,

which allows efficient memory paging and

optimized data structures like triangle-strips. Due to

this block-based simplification and visualization

scheme (9 tiles are visible at one time), height values

can be picked up for each line segment from the

underlying mesh with the highest resolution. Over

meshes with lower resolutions, these height values

must be corrected accordingly.

Schneider et al. 2005 show how to handle

polygonal GIS data in a similar manner. The

polygon borders are treated in a similar way as the

polylines described above. The interior of the

polygon is triangulated and added to the new

geometry, to which a z-offset is added in order to

avoid interference with the terrain and rendering

artefacts. An overview of earlier works in this field

and some foundations on practicable topological

data structures is provided by Lenk 2001.

Both approaches have advantages and

drawbacks. A naïve texture mapping without

dynamic rendering is suitable for remote sensing

raster data like satellite imagery. Vector GIS data

like streets, borders, and landuse areas require a

much higher resolution in order to avoid aliasing and

jagged edges. Especially thin lines must be drawn

with variable width, otherwise they will be filtered

out or look odd in the far distance. Vector

integration requires more complex geometric

operations and is more expensive in the preparation

phase. Overlaying triangulated polygons on top of

the terrain causes huge overheads for large areas.

3 WEB APPLICATION FOR 3D

MAPS

The presented work is embedded in a larger project

that involves a 3D web map server, catalogue

services, several clients and the integration of

various data sources (see Figure 6 for a screenshot of

the web client). We give a brief introduction in the

deployed technologies since they provide important

implications and also constraints for the presented

method for 3D map generation. In this project,

among other issues, we implement two technologies

that have been proposed to the Open Geospatial

Consortium (OGC) as Discussion Papers.

Finally the need for standardization of

geographical 3D web services has been

acknowledged, which led to the first efforts in that

direction. A specification for the delivery of

perspective views of digital terrain models has

already been accepted, the Web Terrain Server

(WTS) – it will be renamed Web Perspective View

Service (WPVS) in future versions. Being an image

based service, it does not support interactive

applications very well. The Web 3D Service

(W3DS) goes one step further (OGC 2005). The

VECTOR BASED MAPPING OF POLYGONS ON IRREGULAR TERRAIN MESHES FOR WEB 3D MAP SERVICES

199

parameters are similar to those of the WTS. The

requested area is described as simple bounding box.

Information on available layers and styles is

provided by the server using the GetCapabilites

request. The GetScene request delivers complete 3D

scenes that can be displayed by web browsers or

integrated in specialized client software. VRML 2.0

must be supported as basic format, but also other

formats can be used. The requested area is described

as simple bounding box. Optional parameters

include a point of interest, a point of camera and a

style for each layer based on the OGC Styled Layer

Descriptor (SLD).

The W3DS follows the concept of a medium

server & medium client scheme, that is, the server is

responsible for the data integration and transfers the

display elements to the client, which is rendering the

scene in real time. Usually browser plugins that

support the specified format are downloaded from

third party companies and used for rendering and

navigation.

Dynamic concepts like continuous LODs for

triangle meshes or streaming of geometry parts are

not incorporated, which is on the one hand beneficial

for the broad applicability, but on the other hand

shows the need for developing standards that cope

with classical GIS features as well as techniques that

are already state of the art in computer graphics.

In our scenario we need to be able to support

desktop computers as well as mobile handsets such

as cell phones equipped with 3D graphics chips.

Consequently, the scenes that we deliver to the client

are static. However, block based visibility schemes,

in which complete tiles with variable size and LOD

are streamed to the client, are still feasible.

The second important technology that we deploy

is the CityGML specification that addresses

interoperability problems during data exchange

between different systems (Kolbe et al. 2005). It has

been developed by the SIG3D (Special Interest

group of the Geodata Infrastructure of North-Rhine

Westphalia, Germany) and proposed to the OGC in

June 2006 as discussion paper. The geometry

description is based on the Geographic Markup

Language (GML), but furthermore includes

materials and textures, prototypic objects,

aggregations and 5 predefined LODs. Although

CityGML is primarily envisaged to completely

describe any 3D city model, and not 2D vector

maps, it is mentioned here because some important

interrelationships between the terrain model and

built objects are addressed. First, it introduces the

concept of closure surfaces, which are used to seal

holes in the ground. Open structures like tunnels and

pedestrian underpasses can be modelled this way.

The triangulation of the terrain is not perforated

since the closure surface belongs to both object and

terrain. Similar to closure surfaces are terrain

intersection curves, which describe the exact

location where a building is touching the ground.

Using these curves, buildings floating over or

sinking into the ground can be avoided.

Both kinds of curves need to be integrated into

the terrain using a similar method as described in the

remaining part of this paper. However, the height

values must be taken from the input curves.

4 APPROACH FOR POLYGON

INTEGRATION

Reviewing the preconditions above, we can state

that:

a) dynamic off-screen rendering is not

supported by standard web browsers,

b) the amount of transmitted data should be

as small as possible, especially when we

consider low bandwidth mobile networks,

c) raster images are very inefficient for

representing polygonal data.

Therefore, geometric mapping should be preferred

over image based mapping. In this paper we pursue

an approach that produces fully vectorized 3D maps.

Polygonal data sets such as building blocks, green

areas, forests, and roads are loaded from 2D GIS

layer files and integrated into a custom Constrained

Delaunay implementation for the terrain. The main

properties of this method is, that the shape of the

terrain is not altered, and z-buffer problems do not

occur, since the resulting terrain is still a single

continuous surface but with integrated areas that

represent the input 2D shapes. After the geometrical

integration operation we can identify the triangles

lying completely inside the area and mark them as

owned by the GIS layer the polygon comes from.

Figure 1: Polygon integration. Comparison of the

situations before (left) and after (right) the mesh

operations. The area becomes visible when different

colours are applied to the triangles.

WEBIST 2007 - International Conference on Web Information Systems and Technologies

200

When the mesh is encoded into the target

transmission format, a style (e.g. a layer colour) can

be applied to these areas which thus become visible.

Figure 1 shows the comparison of the situations

before and after all integration operations for one

polygon. The edges of the mesh which lie exactly on

the polygon border are marked as constrained in

order to avoid the destruction of the area by

subsequent mesh operations.

It should be noted that in this context

“constrained” does not mean that the edge must not

be altered at all. It means that the line shape must be

preserved. Nodes may still be inserted directly on

the constrained edge, splitting it into two and

changing the topology. This case occurs regularly,

when geometries of different layers lie next to each

other, for instance at the transition between different

biotopes, at the border between land and water and

many other cases.

Geometries of different layers may be

overlapping. In this case the last layer will take the

ownership of the triangles beneath. Integrating

several layers in a specific order will look like

painting them on top of each other in a desktop GIS

program.

5 MESH OPERATIONS

In order to achieve the result as displayed above, we

need to focus on the polygon borders. All vertices

can be easily integrated into the mesh, but the

connection between them by edges must be treated

more carefully, since direct lines might lead to

distortions.

The algorithm handles all layer polygons after

each other. The first step is to integrate all vertices

of the outer and inner polygon boundaries into the

triangulated irregular network (TIN) of the terrain.

For each vertex v we find the triangle under v.x / v.y

and compute the height h value h. The new node

n(v.x, v.y, h) is inserted into the TIN and the

triangulation is adjusted (Figure 2). All these

vertices are now part of the TIN as nodes (called

Constrained Nodes here).

For all search operations on the TIN it is very

important to work with an effective spatial index,

otherwise huge overhead computations would slow

down the process. We use our own Quadtree

implementation optimized for triangle meshes.

The next step is to connect all Constrained

Nodes by edges. The general approach is to remove

all triangles that lie between the two Constrained

Nodes of a segment and connect them directly with a

single edge. The holes on either side of the edge are

triangulated afterwards. Although the resulting mesh

would seem to be correct from above, it would mean

to create a ridge or a trench in the surface.

Figure 2: Connecting two nodes by a string of constrained

edges. Situation before insertion (top) with the new

segment as dashed line and the involved original edges

and new nodes in bold style. Situation afterwards (bottom)

with the new segment represented by constrained edges.

Therefore, we need to find the intersection points

of the segment and existing TIN edges and compute

the correct height over the edges (Figure 2). On each

intersection point we perform a node on edge

insertion operation. This deletes the edge and the

adjacent triangles and produces 4 new edges and 4

new triangles. The new nodes can be inserted in a

random order. In fact, the order is given by the

spatial index which is used to find the triangles

beneath the segment and can hardly be predicted.

Now we need to find the new edges under the

segment and mark them as constrained edges,

because their shape should be preserved and not

modified by subsequent operations. In order to avoid

a relatively costly search on the spatial index, we

start with the first Constrained Node and look for

connected edges in the direction of the segment.

This is a topological function and is performed very

quickly. The loop is finished when the second

Polynode is reached.

The last step is to identify all triangles within the

polygon and mark them as owned by the layer which

is currently processed. For this we use the quadtree

again which performs a simple search by the triangle

centre points. The following pseudo-code shows the

complete loop for one layer.

VECTOR BASED MAPPING OF POLYGONS ON IRREGULAR TERRAIN MESHES FOR WEB 3D MAP SERVICES

201

for each polygon p in layer

for each vertex v in p

calculate height h over tin at v

insert new node(v.x,v.y,h) into tin

end

for each segment s in p

n0 = start node of s

n1 = end node of s

if n0 and n1 are connected by edge e

mark e as constraint

else

find intersection points I of s with

edges of the tin

for each p in I

calculate height h over edge e

insert new node(p.x,p.y,h) on e

end

n = n0

while n!= n1

find edge e lying in direction of s

mark e as constraint

n = opposite of n node on e

end

find all triangles T of tin within p

for each t in T

mark t belonging to layer

end

6 GEOMETRY EXTRACTION

Before the finished vector map is transmitted to the

web client, the TIN topology must be broken down

into an indexed triangle array or triangle strip array.

Most formats support a mesh colouring by triangle

so that we can distinguish the integrated areas. The

other possibility is to put all triangles that are owned

by one layer into a separate geometry. Thus we get

one geometry per layer (Figure 3). The advantage is

that we can apply a different style to each layer. A

style can be a simple colour, material, or texture.

Especially generic textures for the natural

environment like grass or crop areas can improve the

visual quality of landscape models enormously, also

for map-like non-photorealistic visualizations.

Additionally we can better influence the reflectivity

for different materials. For instance water surfaces

should be rendered using higher shininess values

than for wood.

7 VECTOR MAP VS. TEXTURE

MAPS

One of our main goals was to reduce the file size of

3D maps as much as possible since they need to be

transmitted to Web Map clients within a low

bandwidth network. In this chapter we compare the

file sizes of vector maps and textured maps with the

same content. The map area has an extent of 2x2 km

and contains layers for water, wood, parks, and

streets. The original DEM consists of 14504

triangles. After the integration of all layers we get

39208 triangles; that is an increase of 170%.

Figure 3: Terrain areas are separated into geometries representing the layers. To each layer geometry a different style can be

applied. Buildings are placed on top of the terrain.

WEBIST 2007 - International Conference on Web Information Systems and Technologies

202

This value depends strongly on the relation

between the LOD of the digitized areas and the LOD

of the terrain. For data sets consisting of larger areas

like geological maps, it is much lower.

We found that compressed VRML encoding is

the most effective one compared to other

compressed ASCII and binary encodings like X3D,

3ds, Viewpoint and others. After encoding the vector

map into VRML and performing a standard ZIP

compression the resulting file is as small as 414 KB

(see Figure 4c).

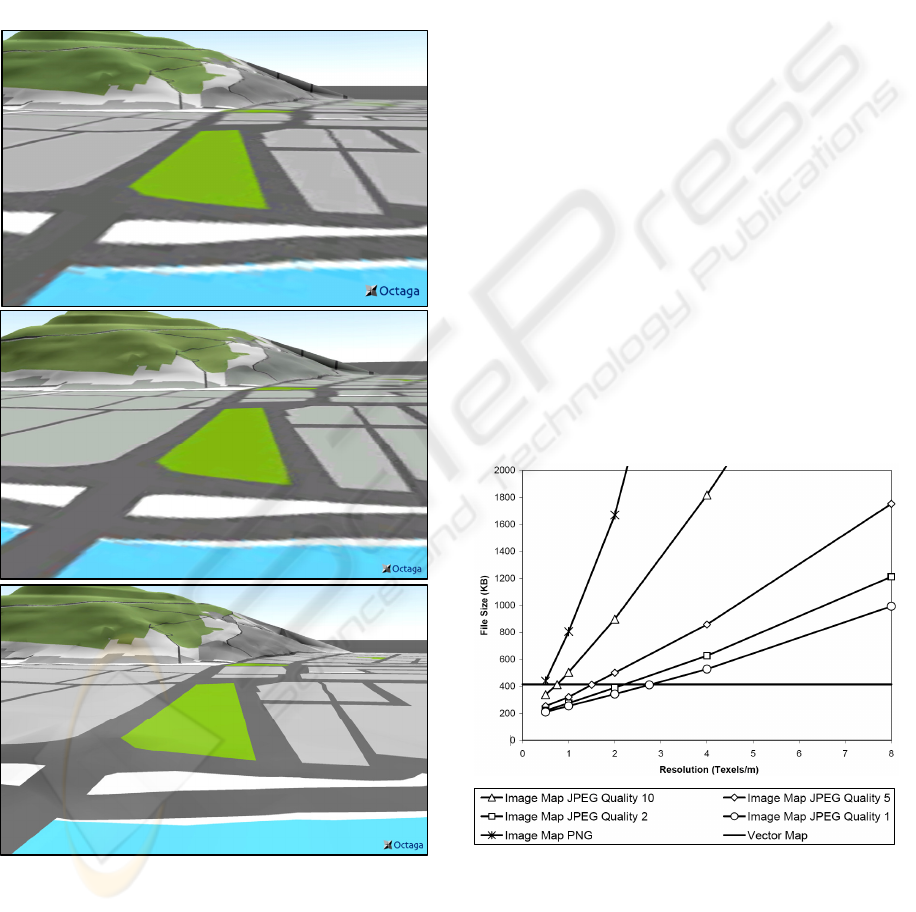
Figure 4: Comparison of texture mapping and geometry

based mapping, a) texture map with low resolution, low

JPEG compression, b) texture map with high resolution,

high JPEG compression, c) vector map with integrated

areas.

Additionally to the vector map we produced

terrain textures by loading the GIS layers into the

commercial GIS package ArcMap and exporting the

display as TIFF raster image with maximum

resolution. The TIFF was post processed by standard

imaging software in order to crop the image to the

correct map extent and to create JPEG and PNG

textures of various resolutions and JPEG

compression ratios. Texture coordinates were

calculated by projecting the images from above and

added to the scene. Although much more

sophisticated texturing schemes are feasible

including dynamic texture trees and multi-texturing,

comparing to this simple approach is still valid if we

consider only a small region, which must be sooner

or later rendered everywhere at the highest available

resolution if the avatar is exploring the whole scene.

Figure 4 shows a comparison of two different

texture maps and the vector map loaded in a

standard web browser plug-in. The textures have

different resolutions and JPEG compression ratios.

The term Texel refers to the pixels of the texture

image. The compression ratio is a compound value

based on the entries in the Huffman encoding table,

ranging from 0 (worst quality) to 12 (best quality).

a) Resolution 1,33 m per texel, JPEG com-

pression 10, file size 413 KB.

b) Resolution 0,5 m per texel, JPEG com-

pression 02, file size 390 KB.

c) Vector map, file size 414 KB.

Figure 5: File sizes of texture maps in relation to image

resolution and quality compared to the equivalent vector

map.

Figure 5 shows how these parameters influence

the texture file size. The mentioned file sizes refer to

the combined size of compressed VRML and JPEG

files. The JPEG textures have also been ZIP

)

VECTOR BASED MAPPING OF POLYGONS ON IRREGULAR TERRAIN MESHES FOR WEB 3D MAP SERVICES

203

compressed. This is usually not done for 3D web

applications, since JPEG is very effective for most

images. However, in the case of rendered vector

graphics the file size could be reduced to 30% - 65%

of the original JPEG file, due to the monotonous

image structure. As can be seen, the 3 scenes have

about the same file size. PNG as an encoding with

lossless compression is in general better suited for

GIS data, but yields unacceptable amounts of data.

Figure 4 shows that higher resolutions should be

preferred when trading off between resolution and

image quality. However, only the vector map

(Figure 4 c) allows rendering crisp edges.

8 CONCLUSIONS AND

OUTLOOK

We showed how to effectively combine 2,5D terrain

models and 2D GIS data - especially polygonal data

– by using mesh integration operations. We can

achieve superior visual quality for representing areas

like forests, streets, water, geological strata, and

others on terrain models. On the downside, the

proposed method involves some additional

computations that naturally increase the response

time. In our current implementation and for the

example above, the polygon integration takes 10

times longer than the initial terrain triangulation. So

this should be done in a pre-processing step if

possible.

Another important aspect is how to apply mesh

reduction algorithms on this kind of meshes for

deriving lower LODs or producing hierarchical data

structures for continuous LOD streaming

(progressive meshes, e.g. Hoppe 1998). Of course,

the interior constrained edges should be preserved as

long as possible so that the map appearance is not

destroyed by edge collapse or vertex removal

operations too early. Basically, the error metric

needs to be adapted so that alterations of interior

edges are charged with a penalty factor. Schroeder

1997 shows how to classify vertices and edges and

how to adjust the quadratic error metric.

The file sizes of vector maps can be further

reduced with mesh compression techniques.

Isenburg and Snoeyink 2002 report a reduction of

about 50% for gzipped VRML files using an ASCII

based encoding of mesh compression Higher

compression ratios can be achieved with binary

encoders that produce optimized bit streams, for

Figure 6: Screenshot of the final Web 3D Map client. The software runs as Java Webstart application and includes a

custom Java3D viewer. Parameters for the OGC GetScene request can be set on the left panel, which include layers, spatial

extent, coordinate system, POI, POC and others. Data courtesy of Land Surveying Office City of Heidelberg.

WEBIST 2007 - International Conference on Web Information Systems and Technologies

204

instance Delphi (Coors and Rossignac 2004).

They use as few bits as possible for describing

the mesh connectivity. Another advantage is that

such compressed binary formats can be decoded

very quickly on the client side, whereas text parsers

tend to be very slow and need many resources (esp.

XML parsers). We are currently investigating

methods to transmit 3D geo data more effectively

since we also need to handle complex 3D city

models that include buildings, textured landmarks,

point objects, and many more. One way could be to

describe only the model structure (the scenegraph) in

an open format like X3D, and to use compressed

binary encoding for the geometry.

ACKNOWLEDGEMENTS

This work has been funded by the Klaus- Tschira-

Foundation (KTS) Heidelberg within the project

SDI-3D - www.heidelberg-3d.de. We thank the

Land Surveying Office of Heidelberg for supporting

us with spatial data.

REFERENCES

Agrawal, A., Radhakrishna, M, Joshi, R.C. 2006.

Geometry-based Mapping and Rendering of Vector

Data over LOD Phototextured 3D Terrain Models.

WSCG 2006 - The 14

International Conference in

Central Europe on Computer Graphics, Visualization

and Computer Vision, Jan. 30 – Feb. 3, 2006, Plzen -

Bory, Czech Republic.

Coors, V., Rossignac, J. 2004. Delphi: geometry-based

connectivity prediction in triangle mesh compression.

In The Visual Computer, International Journal of

Computer Graphics, Vol. 20, Number 8-9, 2004, pp.

507–520.

Haeberling, C. 1999. Symbolization in Topographic 3D

Maps: Conceptual Aspects for User-Oriented Design.

In Proceedings of 19

International Cartographic

Conference ICA ‘99, Ottawa, Canada, pp. 1037-1044.

Hoppe, H. 1998. Smooth view-dependent level-of-detail

control and its application to terrain rendering. In

IEEE Visualization, October 1998, pp. 35-42.

Isenburg, M., Snoeyink, J. 2002. Coding Polygon Meshes

as Compressable ASCII. In Proceedings of Web3D

Symposium'02, Feb. 2002, Tampe, AZ, pp. 1-10.

Kersting, O., Döllner, J. 2002. Interactive 3D

Visualization of Vector Data in GIS. In Proceedings of

the 10th ACM International Symposium on Advances

in Geographic Information Systems - ACMGIS, Nov.

2002, Washington D.C., pp. 107-112.

Kolbe, T.H., Gröger, G., Plümer, L. 2005. CityGML –

Interoperable Access to 3D City Models. In

Proceedings of the Int. Symposium on Geo-

information for Disaster Management. Mar. 21-23,

2005, Delft, The Netherlands.

Lenk, U., 2001, Strategies for integrating height

information and 2D GIS data. In Joint OEEPE/ISPRS

workshop: From 2D to 3D, establishment and

maintenance of national core spatial databases,

October 2001, Hannover, Germany.

Lindstrom, P., Pascucci, V. 2002. Terrain Simplification

Simplified: A General Framework for View-

Dependent Out-of-Core Visualization. In IEEE

Transactions on Visualization and Computer Graphics

Vol. 8 , Issue 3 (July 2002), pp. 239-254.

Open Geospatial Consortium Inc. (OGC) 2005. Web 3D

Service. OGC Discussion Paper, Ref. No. OGC 05-

019.

Schilling, A., Zipf, A. 2002. Generation of VRML City

Models for Focus Based Tour Animations -

Integration, Modeling and Presentation of

Heterogeneous Geo-Data Sources. In Web3D

Conference, 9-12.03.2003, Saint Malo, France.

Schneider, M., Guthe, M., Klein, R. 2005. Real-time

Rendering of Complex Vector Data on 3D Terrain

Models. In Proceedings of the 11

International

Conference on Virtual Systems and Multimedia –

VSMM, Oct. 3-7, 2005, Ghent, Belgium, pp. 573-582.

Schroeder, W.J. 1997. A Topology Modifying Progressive

Decimation Algorithm. In IEEE Proceedings

Visualization '97, pp. 205-21.

Stoter, J.E. 2004. 3D Cadastre. PhD thesis Delft

University of Technology. In: Netherlands Geodetic

Commission NCG : Publications on Geodesy : New

Series, 57. 327 p. ISBN 90-6132-286-3.

Wartell, Z., Kang, E., Wasilewski, T., Ribarsky, W.,

Faust, N. 2003. Rendering Vector Data over Global,

Multi-resolution 3D Terrain. In Proceedings of Joint

EUROGRAPHICS – IEEE TCV Symposium on

Visualization, May 26-28, 2003, Grenoble, France,

pp. 213-222.

Wynn, C. 2001. Using P-Buffers for Off-Screen

Rendering in OpenGL. NVIDIA Corp. white paper.

VECTOR BASED MAPPING OF POLYGONS ON IRREGULAR TERRAIN MESHES FOR WEB 3D MAP SERVICES

205