A NOVEL APPROACH OF ALARM CLASSIFICATION FOR
INTRUSION DETECTION BASED UPON
DEMPSTER-SHAFER THEORY
Guangsheng Feng, Huiqiang Wang
College of Computer Science and Technology, Harbin Engineering University, Harbin, Heilongjiang, China
Qian Zhao
College of Computer Science and Technology, Harbin Engineering University, Harbin, Heilongjiang, China
Keywords: Intrusion detection systems, Dempster-Shafer theory, data fusion, classification.
Abstract: As the number of the alarms is increasingly growing, which are generated by intrusion detection systems
(IDS), automatic tools for classification have been proposed to fulfil the requirements of the huge volume of
alarms. In addition, it has been shown that an accurate classification requires the evidences from different
sources, such as different IDS. Further more, Dempster-Shafer theory is a powerful tool in dealing with the
uncertainty information. This paper proposes multiple-level classification model, which aims to classify the
large sizes of alarms exactly. Experimental results show that this approach has an outstanding capability of
classification. Especially it is quite effective in avoiding alarms grouped into the wrong classes in the case
of short of evidences.
1 INTRODUCTION
Intrusion detection is the process of monitoring
computers or networks for unauthorized entrance,
activity, or file modification(Xiang and Lim, 2005).
Traditional way of intrusion detection is using audit
trail data which is a record of activities on a system
that are logged to file in temporal order. Manual
inspection of these logs is not feasible due to
incredibly large volume of audit data generated by
operating systems. Therefore, many IDS (Intrusion
Detection Systems) sensors are designed to inspect
audit data automatically. For instance, MADAM
ID(Lee and Stolfo, 2000) is a good representative,
which is considered as a bench-mark work for
intrusion detection systems. Most of IDS sensors are
deployed in the local network, so it is too hasty to
hold back the intrusions completely, even though the
intrusive behaviours are detected. To overcome this
disadvantage, IDS sensors based upon the network
traffic package are devised, which are distributed in
the network for detecting intrusions in a wide range.
Obviously, it is possible to detect the intrusive
behaviours in the early time, and thus we can have
more time to against them. However, this method
causes a high false alarm rate. How to accurately
discriminate false alarms from a suspicious alarm set
and reduce the false alarm rate are the main
problems that we need to solve.
To this issue, many researchers have brought
forward lots of promising solutions. Researchers
(Debar, Dacier et al., 1999) proposed a taxonomy for
intrusion detection systems. This taxonomy they
maintained could cover most of the attack types, but
they did not devise an effective approach to detect
some intrusive behaviour, such as abuse-of-privilege
attacks. Considering high false alarm rate usually
caused by new attack types appearing, a data mining
framework was proposed(Lee, Stolfo et al., 1999).
Although this frame might have a strong ability in
detecting new intrusive behaviours, it always needed
sufficient data to recognize those attacks.
Enlightened by the approach of Bayesian event
classification(Kruegel, Mutz et al., 2003), we
propose a new multiple level system with ability of
on-line alarm classification based on the Dempster-
Shafer theory. Experimental results on DARPA1999
dataset show that: 1. our model of classification does
234
Feng G., Wang H. and Zhao Q. (2007).
A NOVEL APPROACH OF ALARM CLASSIFICATION FOR INTRUSION DETECTION BASED UPON DEMPSTER-SHAFER THEORY.
In Proceedings of the Third International Conference on Web Information Systems and Technologies - Internet Technology, pages 234-239
DOI: 10.5220/0001279902340239
Copyright
c
 SciTePress

not need lots of pure data to train; 2. it can avoid
going into wrong class earlier; 3. the false alarm rate
in this system decreased drastically.
The organization of this paper is as follows.
First, a summary of the related works is presented in
Section 2. The mathematical foundations are
provided in Section 3 and the proposed model is
introduced in detail in Section 4. Outcomes attained
by performing the designed experiment are reported
in Section 5 and a section of conclusions follows.
2 RELATED WORKS
Previous researches on alarm classification broadly
fall into the following categories.
1. A heuristic/probabilistic approach(Valdes and
Skinner, 2001) to alarm classification and
correlation has been proposed, where weighted
distance functions are defined to classify and
aggregate alarms. By computing the weighted sum
of similarity indexes among alarm features such as
the announced attack class, IP addresses, TCP/UDP
source and destination ports, timestamps, etc., an
overall similarity index between alarms is obtained.
2. Expert systems have been also used to perform
alarm classification and correlation(Cuppens, 2001;
Cuppens and Miege, 2002). Alarms are classified
and clustered according to suitable distance
measures, and global alarms are produced. Distances
among alarms are computed taking account of
similarity between attack descriptions, source and
target similarity, time similarity, etc.
3. Approaches of alarm classification based on data
mining have been discussed heatedly for more than
one decade. The typical representative is the fast
scalable classifier proposed in (Mehta, Agrawal et
al., 1996). In other academic fields, data mining
based on Bayesian network(Ouali, Cherif et al.,
2006),which is considered as one of the most
popular formalisms for reasoning under uncertainty,
is used for classification.
4. Utilizing a Bayesian decision process for event
classification is proposed in (Kruegel, Mutz et al.,
2003). Instead of the simple, threshold-based
decision process, this process can seamlessly
incorporate available additional information into the
detection decision and aggregate different model
outputs in a more meaningful way. Dempster-Shafer
evidence theory has a close relation with the
Bayesian inference, and can be used for intrusion
detection(Chen and Venkataramanan, 2005).
With respect to the related work, a novel
approach of alarm classification for intrusion
detection based upon Dempster-Shafer theory is
proposed in this paper. The objective is to classify
alarms into corresponding categories accurately and
achieve alarm volume reduction. In particular, the
main contribution is the introduction of a multiple-
level structure and a multiple-stage process, which
have an outstanding capability in classification
proved by the designed experiment.
3 MATHEMATICAL
FOUNDATIONS
3.1 Dempster-Shafer’s Theory of
Evidence
Let
12
,,,
N
…qq q ÎQ
be a set of possible states of a
system, in which all the elements are mutually
exclusive. The set
Q
is often called the frame of
discernment, which represent a set of mutually
exclusive and exhaustive propositions. We will call
the hypotheses
i
H
subset of
Q
, in other words
elements of the power set
2
Q
.
Evidence on a subset
B ⊂Θ
is represented with a
basic probability assignment (bpa)
() 0mB ≥
and
subsets with non null bpa are called focal elements,
which have the following properties:
The belief function
()Bel B
gives the amount of
evidences which imply the observation of B:
() ()
CB
B
el B m C
⊂
=
∑
The plausibility function
()Pl B
can be seen as
the amount of evidences which do not refute B:
() ()
CB
Pl B m C
φ ≠
=
∑
I
3.2 Dempster’s Rule for Combination
Suppose
A ⊂Θ
and
1
()mA
and
2
()mA
are the basic
probability assignments from two independent
observers in the same frame of discernment.
Dempster’s rule for combination consists of the
orthogonal sum which combines pieces of evidence
from independent observation sources:
:2 [0,1]m
Θ
→
(1)
() 1
B
mB
⊂Θ
=
∑
(2)
() 0m
φ
=
(3)
A NOVEL APPROACH OF ALARM CLASSIFICATION FOR INTRUSION DETECTION BASED UPON
DEMPSTER-SHAFER THEORY
235

where
K
is the conflict coefficient and
12
11 2 2
() ()
AA
KmAmA
φ =
=
∑
I
. Obviously,
1
K
≠
. If A
φ
=
,
we can get equation(5):
If
1K =
, the two evidences are completely conflict,
otherwise, they are consistent with each other
totally.
The formula (4) can be generalized as:
where
11 2 2
( ) ( )... ( )
ii
nn
A
K
mAm A mA
φ =
=
∑
I
.
4 THE CLASSIFICATION
MODEL
4.1 The Overall Structure of Classifier
Figure 1: Classification Model.
The network attacks are usually classified into four
categories, which follow the general classification of
intrusion detection as given in Evaluating Intrusion
Detection Systems: The 1998 DARPA Off-Line
Intrusion Detection Evaluation (Lippmann, Haines
et al., 2000): 1. DoS (Denial of Service); 2. Probe; 3.
U2R (User to Root); 4. R2L (Remote to Local).
Thus, the alarms are classified into corresponding
groups, such as DoS alarm, Probe Alarm, etc.
The overall structure of classifier is shown in
Figure 1. we construct a multi-level classification
model with three stages and one fusion engine,
whose structure takes a similar form with (Xiang
and Lim, 2005). However, the most different aspect
between them is that it utilizes the data fusion engine
to help identify type of attack alarms exactly. This
model consists of two parts: alarm classification
module and date fusion engine. In alarm
classification module: IDS sensors accept network
traffic packages from the Internet ceaselessly, and
transit them into alarm messages. Then, the alarm
messages generated by IDS sensors are translated
into intrusion detection message exchange format
(IDMEF) by the alarm classifier, which has been
proposed as standard format of alarm reporting by
the IETF(Perdisci, Giacinto et al., 2006).
After the formatted alarm messages generated,
classifier will process them to find anomaly,
suspicious or normal behaviours with the assist of
data fusion engine. If an easily identified alarm
exists, it will be classified into the corresponding
category. Otherwise, it will be considered as a
suspicious one. In other words, if network
behaviours present obvious traits belonging to the
normal or anomaly, they will be classified into
corresponding category Normal or Anomaly.
Whatever the network behaviour belongs to, a belief
value attached to the processed data is generated.
Basic probability assignments are determined
dynamically by data fusion engine, which will be
changed with this system running. Likewise, if the
first stage is finished, the processed alarm will go
into the next stage.
Date fusion engine is based upon the Dempster-
Shafer theory, of which the most important aspect is
that it concerns the combination of evidences
provided by different sources. In the first level, data
sources are sensors deployed in the network
environments; in the second level, the data sources
are the alarms produced by the Alarm Classifier; the
third level considers the alarms generated by its
above classifier as the data sources. A detailed
introduction to data fusion engine will be presented
in the coming section.
4.2 Data Fusion Engine
4.2.1 Frame of Discernment
1
L
evel
Θ
The frame of discernment
1
L
evel
Θ consists of two
possibilities
Normal
and
A
nomaly
. Concerning alarm
S:
1
{, }
Level
Normal Anomaly
Θ
=
,
Normal
means
S
is
secure, but
A
nomaly
means not. For this frame, the
power set has three focal elements:
hypothesis
1
{}HNormal
=
,
2
{}
H
Anomaly=
and
12
11 2 2
12
() ()
() ()
1
AAA
mAmA
mA m m A
k
=
=⊕ =
−
∑
I
,
(4)
12 12
() () 0mmAmm
φ
⊕=⊕=
(5)
11 2 2
12
() ()...()
... ( )
1
ii
nn
A
n
mAmA m A
mm mA
K
⊕⊕⊕ =
−
∑
I
(6)
WEBIST 2007 - International Conference on Web Information Systems and Technologies
236

2{, , ,{ , }}U Normal Anomaly Normal Anomaly φ
Θ
==
.
4.2.2 Basic Probability Assignment
Concerning the frame of discernment
1
{, }
Level
Normal AnomalyΘ=
,
Normal Anomaly
φ
=I
means
that
Normal
and
A
nomaly
are mutually exclusive.
Define the function of basic probability assignment
m :
({ , }) [0,1]P Normal Anomaly →
, where
() 0m
φ
=
and
()( )({, })1m Normal m Anomaly m Normal Anomaly++ =
. In
this equation,
()mNormal
denotes the believable
value of data
S
supporting normal behaviours
()mAnomaly
; denotes the value of
S
supporting
anomaly behaviours;
({ , })m Normal Anomaly
=
1( )( ) ( )m Normal m Anomaly m Suspicious−− =
denotes the value of
S
belonging to uncertainty. In
other words, it is uncertain that data
S
should belong
to set
Normal
or
A
nomaly
. In order to interpret this
function, several definitions are introduced.
Definition 1. Expected Value Let
X
be a
numerically valued discrete random variable with
sample space
Ω
and distribution function
'( )mx
.
The expected value E(X) is defined by
() '()
x
E
Xxmx
∈Ω
=
∑
, provided this sum converges
absolutely.
Definition 2. Standard Deviation of
X
. Let
X
be a
numerically valued random variable with expected
value
()EX
. Then the variance of
X
, denoted
by
()VX
, is
2
() (( ()))VX E X EX=−
. The standard
deviation of
X
, denoted by
()DX
, is defined
by
() ()DX V X=
.
Definition 3. Deviation from Expectation Let
X
be a random variable which exists the expected
value
()
E
X
and standard deviation
X
σ
. The
function of deviation from expectation is defined
by
()
()
X
x
EX
x
ξ
σ
−
=
, which means that the number
of standard deviations between it and expected
value.
The basic probability assignment is defined
based upon the function of deviation from
expectation. The reason is that the function of
expectation from deviation is better than that of
probability distribution in reflecting the degree of
abnormality. According to the Chebyshev Inequality
2
()
(())
VX
PX EX
ε
ε
−≥≤
, probability distribution is
descending exponentially with the expected value
augmenting. Thus, the deviation from expected
value is consistent with the probability distribution.
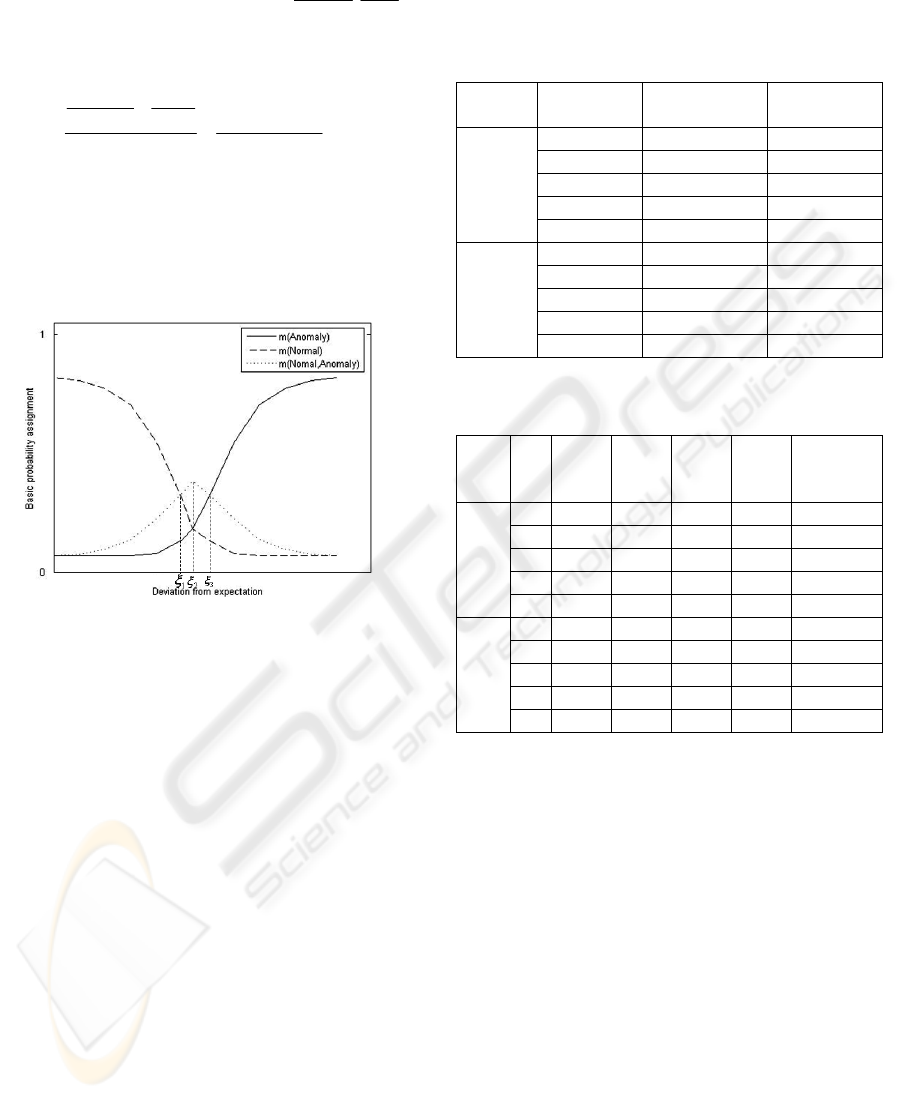
Figure 2(Jian-Wei, Da-Wei et al., 2006) shows
the basic rule of designing basic probability
assignment. When the deviation from expected value
of eigenvalue is small (
1
ξ
ξ
<
), the expected value is
in a normal range. So the believable value of
supporting
N
omal
is larger. Meanwhile, the value of
supporting
A
nomaly
is small. With the expected
value augmenting, the value supporting
N
omal
is
descending rapidly, but the value supporting
A
nomaly
rises gradually. Thus, in a critical
point
2
ξ
ξ
=
, the value supporting uncertainty gains
maximum. At the same time, the value supporting
A
nomaly
will exceed the one supporting
N
omal
in
this critical point. After this point, the value
supporting uncertainty will be descending, but the
value supporting
A
nomaly
will rise rapidly. When
reaching at the point
3
ξ
(
3
ξ
ξ ≥
), the value
supporting
A
nomaly
will grow lager than the one of
supporting uncertainty.
According to the principle rule of basic
probability assignment, we have gained three points:
1
ξ
,
2
ξ
,
3
ξ
which are well proper to discriminate
normal and anomaly alarms through training
experimental data. And
()mNormal
,
()mAnomaly
and
({ , })m Normal Abormal
are adjusted to gain a better
capability for classification.
As described in Figure 1, the category
Suspicious
is confined in
13
[, ]
ξ
ξ
. For a certain
alarm, it will be considered as
Normal, Suspicious or
Anomaly by sensors with the help of date fusion
engine
. How can the gross categories be classified
into grinding ones? As shown in the
Figure 1:
Classification Model
, every classifier has a capability
to recognize those alarms with a different degree,
which depends on what kind of approach is utilized.
In our system, we use the distance between alarms
proposed in (Perdisci, Giacinto et al., 2006) for
classification.
With respect to the capability of classifier, we
give the problem formalization. Given an alarm
A
,
let
A
S
W
be a believable value of classifier
S
, which
means
S
has the probability of
A
S
W
to discriminate
alarm
A
from other normal and anomaly alarms.
Suppose a sample space
Ω
which consists of n
variable
A
and m other alarms, if
S
can
distinguish
i
N
A in the i
th
experiment and the same
experiment is totally performed
P
times, the
A NOVEL APPROACH OF ALARM CLASSIFICATION FOR INTRUSION DETECTION BASED UPON
DEMPSTER-SHAFER THEORY
237

believable value
A
S
W
of
S
will be in
11
[,]
()
PP
ii
ii
NN
nmP nP
==
+
∑∑
.
Simply, the believable value
A
S
W
of
S
is defined by:
11
1
(2 )
()
22()
A
PP
ii
P
ii
i
i
S
NN
nm N
nmP nP
W
nn mP
==
=
+
+
+
==
+
∑∑
∑
.
Apparently, when
S
can identify all the alarms
belonging to type
A,
A
S
W
gains its maximum
value
1
A
S
W =
. Otherwise,
A
S
W
will get the
minimum
0
A
S
W =
, if
S
can not discern any alarm
which belongs to type
A.
Figure 1: Basic Probability Assignment.
4.2.3 Frame of Discernment
2Level
Θ
After the first step of classifying alarms generated
by IDS sensors into corresponding categories,
continuously, the basic probability assignment
should be computed in the frame of
discernment
2
{,,2,2}
Level
PROBE DOS U R R LΘ=
. As
discussed in Section 4.2.2, the basic probability
assignment is defined based upon the function of
deviation from expectation; node
Anomaly and
Suspicious are considered as the data sources on
which data fusion engine works. Notice that each
alarm generated by the classifier has an equal
trustworthiness to this classifier, thus the result
computed by data fusion engine, should multiply
with the trustworthiness of source alarm, and then
the product servers as the final combined result. To
avoid the alarm being classified into the wrong class
earlier, a threshold is introduced to control the
process.
5 EXPERIMENT
Table 1: Result of Classification on the First Level for
Two Weeks.
Week Day
Number of
Anomaly
Number of
Suspicious
Monday 135 812
Tuesday 293 659
Wednesday 410 513
Thursday 504 448
Fourth
week
Friday 627 311
Monday 739 208
Tuesday 857 95
Wednesday 881 76
Thursday 878 83
Fifth
week
Friday 893 71
Table 2: Result of Classification on the Second Level for
Two Weeks.
Week Day
N
umbe
r
of
Probe
Number
of
DOS
N
umbe
r
of
U2R
N
umbe
r
Of
R2L
Number
of
No-Class
Mon. 112 118 56 23 638
Tue. 121 146 79 25 581
Wed. 133 153 93 51 493
Thu. 189 171 128 79 385
Fourth
week
Fri. 210 186 143 92 307
Mon. 237 198 156 145 211
Tue. 254 225 174 173 126
Wed. 276 256 191 193 32
Thu. 293 263 184 195 26
Fifth
week
Fri. 287 259 187 203 28
During the first three weeks, our classification
system was adjusted. Then, we used the traffic in a
certain period from Monday of the fourth week to
the Friday of the fifth week for performance test. A
summary of the obtained results for two considered
weeks is reported by Table 1, which represent the
total number of alarms for each day caused by
anomaly and suspicious behaviours respectively.
As shown in Table 1, in the first three days of the
two weeks, the number of abnormal alarms is less
than the number of suspicious alarms. In the middle
days of the two weeks, the number of anomaly
alarms has a great rise. On the contrary, the number
of suspicious alarms reducing rapidly. Until the forth
day the number of anomaly alarms is larger than the
other one. At the last two days, both of the numbers
are in a stable level. Owing to being short of
evidences in the first days, over half of the alarms
are classified into the
Suspicious. With the
WEBIST 2007 - International Conference on Web Information Systems and Technologies
238

experiment going on, more and more evidences are
gained, so the number of suspicious alarms is
descending.
Table 2 reports the result of classification on the
second level. During the first days, all the numbers
of the different type alarms are very low, which is
caused by the first level, and it could not
discriminate the anomaly alarms from suspicious
ones widely. However, the following days, all of the
numbers ascend greatly, until reaching stable states.
6 CONCLUSIONS
Conventional approaches of alarm classification are
always caused alarms going into the wrong classes
in the early time especially when the evidences used
to classify are in short. To overcome this
shortcoming, this paper proposes a multiple-level
classification model based on the Demper-Shafer
theory. Experiment on DARPA1999 dataset
demonstrates the superiority of our new approach in
handling this problem.
Although the proposed approach of alarms
classification looks promising, more work needs to
be done such as: 1. how to react the intrusions
relating to the classified alarms automatically? 2.
There are still some indistinguishable alarms and
how to handle them?
ACKNOWLEDGEMENTS
This work was supported by Specialized Research
Fund for Doctoral Program of Higher Education of
China (NO.20050217007). In the meanwhile, we
thank the anonymous reviewers for their very
instructive suggestions.
REFERENCES
Chen, T. M. and Venkataramanan, V., 2005. Dempster-
Shafer Theory for Intrusion Detection in Ad Hoc
Networks. Ad Hoc and P2P Security: 35-41.
Cuppens, F., 2001. Managing Alerts in a Multi-Intrusion
Detection Environment. In 17th Annual Computer
Security Applications Conference(ACSAC'01) , New
Orleans, LA. IEEE Press.
Cuppens, F. and Miege, A., 2002. Alert Correlation in a
Cooperative Intrusion Detection Framework. In IEEE
Symposium on Security and Privacy, Oakland, USA,
IEEE Press.
Debar, H., Dacier,M., et al., 1999. Towards a Taxonomy
of Intrusion-Detection Systems. Computer Networks
31: 805-822.
Jian-Wei, Z., Da-Wei, W., et al., 2006. A Network
Anomaly Detector Based on the D-S Evidence
Theory. Journal of Software 17(3): 463-471.
Kruegel, C., Mutz, D., et al., 2003. Bayesian Event
Classification for Intrusion Detection. In Proceedings
of the 19th Annual Computer Security Applications
Conference, Los Alamitos, USA. IEEE Press.
Lee, W. and Stolfo, S. J., 2000. A Framework for
Constructing Features and Models for Intrusion
Detection Systems. In ACM Transactions on
Information and System Security, ACM Press.
Lee, W., Stolfo, S. J., et al., 1999. Data Mining
Framework for Building Intrusion Detection Models.
In 1999 IEEE Symposium on Security and Privacy.
IEEE Press.
Lippmann, R., Haines, J. W., et al., 2000. The 1999
DARPA Off-line Intrusion Detection Evaluation.
Computer Networks 34(4): 579-595.
Mehta, M., Agrawal, R., et al., 1996. SLIQ: A Fast
Scalable Classifier for Data Mining. In Conference on
Extending Database Technology (EDBT'96), Avignon,
France, 1996: 18-33.
Ouali, A., Cherif, A. R., et al., 2006. Data Mining Based
Bayesian Networks for Best Classification.
Computational Statistics & Data Analysis 51(2): 1278-
1292.
Perdisci, R., Giacinto, G., et al., 2006. Alarm Clustering
for Intrusion Detection Systems in Computer
Networks. Engineering Applications of Artificial
Intelligence 19(4): 429-438.
Valdes, A. and Skinner, K., 2001. Probabilistic Alert
Correlation. Recent Advances in Intrusion Detection.
In 4th International Symposium, RAID 2001,Lecture
Notes in Computer Science. Berlin,German. Springer
Press. 2001: 54-68.
Xiang, C. and Lim, S. M., 2005. Design of Multiple-Level
Hybrid Classifier for Intrusion Detection System.
Machine Learning for Signal Processing, IEEE Press.
A NOVEL APPROACH OF ALARM CLASSIFICATION FOR INTRUSION DETECTION BASED UPON
DEMPSTER-SHAFER THEORY
239