
EZK: A ZERO KNOWLEDGE TOOL FOR GENERATING,
HANDLING, AND SECURING ELECTRONIC BILLS OF LADING
Andrea Visconti
Dipartmento di Informatica e Comunicazione, Università degli Studi di Milano, via Comelico 39/41, Milano, Italy
Keywords: Blind merchandise counts, electronic bill of lading, EDI, digital signature, zero-knowledge, cryptography.
Abstract: EZK is a tool for generating, handling, and securing electronic bills of lading. EZK implements the
cryptographic protocol suggested by Pagnoni and Visconti in (Pagnoni and Visconti, 2006), cryptographic
protocol that is based on a shipper-carrier-holder model. This protocol makes use of (a) blind merchandise
counts, or zero-knowledge counts, − that is, counts that do not reveal any information about the quantities
actually counted, − (b) secure timestamps, and (c) digital signatures. We show how EZK generates and
handles order e-BOLs and how the cryptographic techniques implemented in EZK make a number of
common fraud schemes impossible.
1 INTRODUCTION
A bill of lading (BOL, for short) is a negotiable
document, that is, a document the physical
possession of which is sufficient evidence of a
certain set of rights. Examples of negotiable
documents are: phone card, bearer bonds, bus
tickets, etc. Negotiable documents are subject to
many kinds of security threats – forgery, duplication,
etc. – and pose particular challenges in the context
of electronic data interchange (ISO/TS 20625,
2002).
An electronic bill of lading (e-BOL) may be
designed as either a bearer, or an order document.
Modelling digital bearer documents is a quite
challenging task that requires a strong notion of
original copy of a file. This problem has been well
studied by researchers working in the area of e-cash,
or digital cash – most notably by Chaum (Chaum,
1988), Okamoto et al. (Okamoto and Ohta, 1992)
and Brands (Brands, 2001). Endorsed, or order,
digital BOLs are easier to model: digital signatures
can be used for endorsement, thus providing a first
measure of originality to the document.
This paper introduce EZK a cryptographic tool
for generating, handling, and securing an order e-
BOL, that is, a digital bill of lading that stores all
relevant shipping information in a way that can be
safely used for all payment purposes. EZK
implements the cryptographic protocol suggested by
Pagnoni and Visconti in (Pagnoni and Visconti,
2006), cryptographic protocol that is based on a
shipper-carrier-holder model. The relevant features
of this tool are (a) blind merchandise counts, – that
are counts with no previous information about
merchandise quantities, – separately done by the
shipper, carrier, and holder; (b) non repudiability of
such counts and (c) non forgery of the e-BOL itself.
This paper is organized as follow: Section 2
discusses how to generate and handle e-BOLs;
Section 3 discusses how to secure e-BOLs; Section 4
presents tests and results of our tool. Finally,
conclusions and future work are briefly discussed in
Section 5. In the sequel, we shall assume readers to
be familiar with both zero-knowledge protocols and
digital signatures, and refer respectively to (Menezes
et al., 1997) and (Stallings, 2006) for a basic
introduction to these topics.
2 GENERATING E-BOLS
An easy way for generating and handling e-BOLs is
to implement the cryptographic protocol (Pagnoni
and Visconti, 2006) based on a shipper-carrier-
holder model. In this section, we briefly present the
main ideas of the protocol. We shall assume the
existence of five actors in our model: Shila (S) the
shipper, Carl (C) the carrier, Hans (H) the holder, a
bank (B) for payment purposes, and a Trusted Third
238
Visconti A. (2007).
EZK: A ZERO KNOWLEDGE TOOL FOR GENERATING, HANDLING, AND SECURING ELECTRONIC BILLS OF LADING.
In Proceedings of the Third International Conference on Web Information Systems and Technologies - Society, e-Business and e-Government /
e-Learning, pages 238-241
DOI: 10.5220/0001280102380241
Copyright
c
SciTePress

Party (TTP) in charge of the generation, distribution,
and maintain all cryptographic keys.
Setup Procedure. Before shipping the
merchandise, EZK needs some information such as
public and private keys of each actor, destination
and type of merchandise and e-BOL identifier. This
information will be generated by TTP during the
setup procedure. For these reasons, shipper Shila
asks TTP to begin setup process. The Trusted Third
Party generates:
public (P
S
, P
C
, P
H
, P
B
, P
TTP
) and private (σ
S
, σ
C
,
σ
H
, σ
B
, σ
TTP
) keys for each actor, and
publishes public keys on its repository;
numbers p and g, where p is a large prime, and
g is a generator of Z
p
, with 1<g<p. This two
numbers will be used by actors for counting
merchandise (see Section 3.3) and, for this
reason, p and g are public numbers. TTP
publishes both p and g on its repository;
a binary timestamp T (see Section 3.1 for
details) that will be used as identification
number of the e-BOL.
Shipping merchandise procedure. This
procedure is done by Shila, Carl, and Hans. Shila:
generates a blank e-BOL
e-BOL = (--, merchandise info, --, --)
computes her blind count K
S
(see Section 3.3
for details) based on Hans’ order and signs K
S
with her private key σ
S
;
fills out the blank e-BOL with (a) signed blind
count σ
S
(K
S
), and (b) e-BOL’s identifier ID,
that is ID=(T, σ
S
(T), --, --).
e-BOL = (ID, merchandise info, σ
S
(K
S
), --)
transmits the e-BOL to carrier Carl, and
delivers the ordered merchandise to him.
Carl:
computes his blind count K
C
;
checks if Shila’s blind count K
S
and Shila’s
timestamp are respectively equal to K
C
and T.
If both the numbers are correct, Carl accepts
e-BOL and merchandise, else he rejects;
if he accepts, Carl signs blind count K
C
with his
private key σ
C
;
fills out the e-BOL with (a) his signed blind
count σ
C
(K
C
), and (b) e-BOL’s identifier ID,
that now is ID=(T, σ
S
(T), σ
C
(T), --)
e-BOL = (ID, merchandise info, σ
S
(K
S
), σ
C
(K
C
))
transmits the e-BOL to holder Hans, and
delivers the ordered merchandise to him.
Again, Hans:
computes his blind count K
H
;
checks Shila’s blind count K
S
, Carl’s blind
count K
C
, Shila’s timestamp and Carl’s
timestamp. If the four numbers are correct,
Hans accepts e-BOL and merchandise, else he
rejects;
if he accepts, he fills out the e-BOL with e-
BOL’s identifier ID, that now is ID=(T,
σ
S
(T), σ
C
(T), σ
H
(T))
e-BOL = (ID, merchandise info, σ
S
(K
S
), σ
C
(K
C
))
transmits the e-BOL to Shila and Carl.
encrypts the e-BOL with public key of the bank
P
B
(e-BOL) and transmits it to bank B for
payment purposes.
Validation procedure. This procedure is done
by bank B. The bank decrypts the e-BOL received
from Hans with its private key σ
B
, and checks all
timestamps and blind counts recovered from the e-
BOL. If all data are not corrupted or altered, bank B
begins the payment procedure, else begins the fraud
control procedure.
Payment procedure. The bank pays Shila for
the merchandise and Carl for his services and then
sends the e-BOL signed with its private keys σ
B
to
Shila and Carl as a payment acknowledgement.
Upon checking that her bank account has been
properly credited, Shila signs the e-BOL with her
private key σ
S
and send the signed e-BOL to the
bank. Bank B stores Shila’ signed e-BOL as proof of
payment. Carl will do the same operation with his
private key σ
C
.
Fraud control procedure. The bank discovers
actors that try to cheat (Pagnoni and Visconti, 2006)
submitting the e-BOL to bank B twice with the same
or different timestamps T, filling out the e-BOL with
erroneous blind counts, modifying the blind count
after forwarding merchandise, trying to fake an e-
BOL ex-novo, and so on. Checking all timestamps T
and blind counts, the bank will discover dishonest
actors and stop all payment procedure.
3 SECURING E-BOLS
An easy way for securing e-BOL is combining
several cryptographic techniques for preventing
fraud schemes. We choose digital signatures, zero-
knowledge representation, and encryption
operations. Before introducing the cryptographic
techniques used in our application, we would list
few properties of signed e-BOLs. Signed e-BOL (a)
constitute a sure proof of the author’s identity, (b)
cannot be repudiated by the signer, and (c) cannot be
altered by any evil actor. In order to achieve
previous properties, EZK uses secure binary
timestamps, digital signatures, unforgeable blind
counts, and encryption operations.
EZK: A ZERO KNOWLEDGE TOOL FOR GENERATING, HANDLING, AND SECURING ELECTRONIC BILLS OF
LADING
239
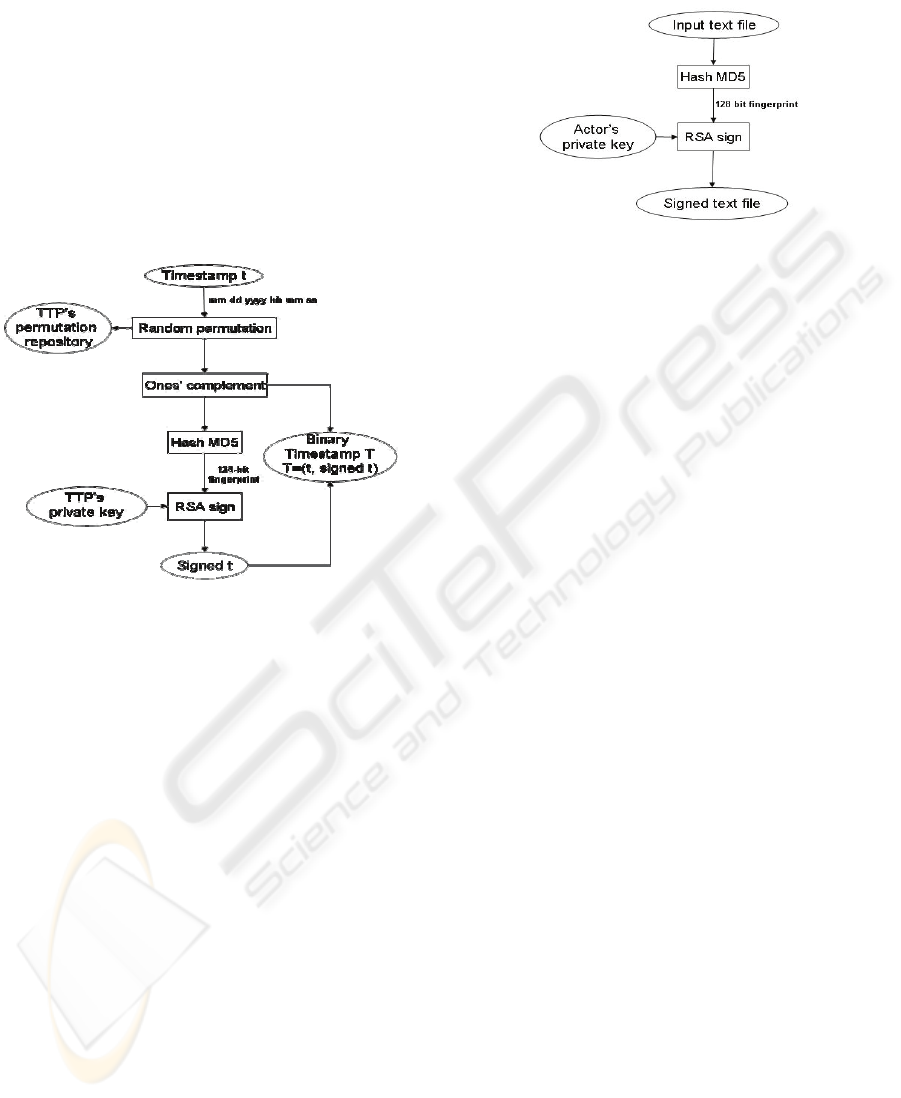
3.1 Binary Timestamp
For generating a secure binary timestamp T (see
Figure 1), EZK (a) creates a timestamp t of the
actual transaction (month, day, year, hour, min, sec),
(b) subjects the timestamp t to a secret random
permutation, (c) computes ones’ complement of the
previous permutation, (d) creates a hash file (see
section 3.2 for details), and then (e) signs the output
hash file with TTP’s secret key σTTP. Moreover,
TTP securely stores the secret random permutation
to be used for investigating possible cheating
schemes.
Figure 1: TTP generates binary timestamp T.
3.2 Digital Signature
For signing timestamp t (see Figure 1), endorsing
order e-BOL, and implementing all signature
operations EZK will use an asymmetric
cryptographic algorithm. The main problem of
signature operations is that apply a signature to large
files is a very time-consuming operation.
Unfortunately, if we ship a big number of different
items, our e-BOL will be a large text file. For this
reason, we cannot directly sign it, but we can solve
the problem by means of a hash function. Let us
explain how.
A hash function is function that provides a way
of creating a small digital fingerprint, or so called
message digest, for an arbitrarily long input file.
Therefore, we can (a) input our large text file to a
hash function algorithm that produce a small digital
fingerprint and then, (b) sign the small fingerprint.
We choose MD5 message digest algorithm as
hash function and RSA as asymmetric cryptographic
algorithm for signature operations. MD5 algorithm
takes as input any file of arbitrary size and produces
as output a 128-bit fingerprint. Then, we can quickly
sign this 128-bit fingerprint by means of RSA (See
Figure 2) with keys of 1024 bits.
Figure 2: Signature operations.
Both MD5 and RSA algorithms were taken from
OpenSSL library (OpenSSL, 2006). These
cryptosystems need specific function for generating
and manipulating large primes, functions
implemented in OpenSSL library (OpenSSL, 2006).
3.3 Blind Counts
For counting merchandise, we introduce blind
counts, a technique based on zero-knowledge
representation (Menezes 1997). Blind counts are the
representation of actual merchandise counts, that do
not reveal any information about the specific
quantities counted of each item.
Each actor can compute its blind merchandise
counts K
A
by counting the quantity q
i
of each item i
and then executing this operation:
K
A
= g
1
q
1
· g
2
q
2
· … · g
n
q
n
mod p
where g
i
are random number of Z
p
that identify n
different items. Numbers g
1
… g
n
are written onto the
e-BOL by shipper Shila before computing her blind
count K
S
. Altering the value of blind counts K
A
will
be computationally unfeasible because evil actors
should invert multi-logarithmic functions over finite
fields and know actors’ private keys for signing the
new fake value.
3.4 Encryption
For protecting data stored in the e-BOL that will be
sent over the Internet, EZK makes use of encryption.
As mentioned in Section 3.2 encryption and
decryption operations, applied to large input files,
are very time consuming operations and we can use
it only few times. In our application, encryption and
decryption operations are respectively done by Hans
and bank B just one time. Hans encrypts the e-BOL
with the public key of the bank P
B
and sends it to
WEBIST 2007 - International Conference on Web Information Systems and Technologies
240

bank B. The bank decrypts the e-BOL and starts the
validation procedure. Encryption and decryption
operation are all based on RSA cryptographic
functions implemented in OpenSSL library.
4 TESTS AND RESULTS
EZK is a stand-alone and portable application
developed in ANSI C, which runs on any
architecture and any operating system having
OpenSSL library installed (OpenSSL, 2006). EZK
has been tested on Intel
®
Pentium
®
III, at 1GHz,
with 1Gb of RAM under Linux. For computing the
time spent by EZK during signature operations and
encryption/decryption, we used UNIX command
time. This command shows us:
the total number of CPU-seconds spent by the
process in user mode (U);
the total number of CPU-seconds spent by the
process in kernel mode, that means time spent
by the system on behalf of the process (S);
the elapsed real time spent by the process (R).
The length of the keys used by EZK for data
encryption/decryption and signature operations was
1024 bits. All tests have been repeated ten times and
the average values, expressed in second, are
presented in the following tables.
Table 1: Computation times for the generation of RSA key
pairs.
RSA key size (bits) R (secs) U (secs) S (secs)
512 0,179 0,164 0,003
768 0,385 0,364 0,003
1024 2,815 2,565 0,012
2048 21,596 20,061 0,081
Table 2: Computation times for generating and signing a
128-bit fingerprint.
Key size (bits) R (secs) U (secs) S (secs)
512 0,028 0,021 0,004
1024 0,038 0,030 0,005
2048 0,083 0,074 0,006
Table 3: Computation times for verifying digital
signatures previously computed in Table 2.
Key size (bits) R (secs) U (secs) S (secs)
512 0,020 0,014 0,003
1024 0,022 0,017 0,004
2048 0,028 0,021 0,004
Table 4: Computation times spent by Hans for encrypting
the e-BOL.
Plaintext (Kbytes) R (secs) U (secs) S (secs)
1 0,008 0,003 0,003
8 0,023 0,016 0,004
32 0,080 0,061 0,004
128 0,233 0,226 0,004
Table 5: Computation times spent by bank B for
decrypting the e-BOL.
Ciphertext (Kbytes) R (secs) U (secs) S (secs)
1 0,268 0,251 0,003
8 1,726 1,576 0,012
32 7,574 6,903 0,041
128 24,805 24,116 0,072
5 CONCLUSIONS
We have presented a tool based on cryptography
techniques for generating, handling, and securing
electronic bills of lading. In particular, we have
shown how it is possible to generate a secure e-BOL
using cryptographic techniques, e-BOL that cannot
be forged, repudiated, or altered. The strength of
EZK is ensured by the computational complexity of
inverting multi-logarithmic functions over finite
fields, complexity that makes forging our digital
BOLs computationally unfeasible.Future research
will focus on designing secure XML order e-BOLs
that can be generated and handled by a web server.
REFERENCES
Brands, S.A., 2001. Rethinking Public Key Infrastructure
and Digital Certificates Building in Privacy. The MIT
Press, Cambridge.
Chaum, D. et al., 1988, Untraceable electronic cash.
Advances in cryptology – CRYPTO’88, LNCS 403.
ISO/TS 20625, 2002, Electronic data interchange for
administration, commerce and transport (EDIFACT),
available at http://www.iso.org/.
EDI 2006, Electronic Data Interchange, available at
http://www.edi-guide.com/.
Menezes, A.J. et al., 1997. Handbook of Applied
Cryptography. CRC Press, New York.
Okamoto, T. and Ohta, K., 1992, Universal electronic
cash. Advances in cryptology,CRYPTO’91, LNCS 576.
OpenSSL 2006, OpenSSL library, available at
http://www.openssl.org
Pagnoni, A. and Visconti, A., 2006. Electronic Bill of
Lading: a Cryptographic Protocol. In e-commerce
2006, IADIS International Conference. IADIS Press.
Stallings, W., 2006. Cryptography and Network Security
4th Ed.
EZK: A ZERO KNOWLEDGE TOOL FOR GENERATING, HANDLING, AND SECURING ELECTRONIC BILLS OF
LADING
241
