
ACCELERATING XPATH AXES THROUGH STRUCTURAL
PARTITIONING
Olli Luoma
Department of Information Technology, 20014 University of Turku, Finland
Keywords:
XML, XPath, XML databases.
Abstract:
The query evaluation algorithms of practically all XML management systems are based on structural joins,
i.e., operations which determine all occurrences of parent/child, ancestor/descendant, preceding/following
etc. relationships between node sets. In this paper, we present a simple method for accelerating structural
joins which is very easy to implement on different platforms. Our idea is to split the nodes into disjoint
partitions and use this information to avoid unnecessary structural joins. Despite its simplicity, our proposal
can considerably accelerate XPath evaluation on different XML management systems. To exemplify this, we
describe two implementation options of our method - one built from the scratch and one based on a relational
database - and present the results of our experiments.
1 INTRODUCTION
In many modern applications areas, such as bioinfor-
matics and Web services, there is a need to efficiently
store and query large heterogeneous data sets marked
up using XML (W3C, 2006a), i.e., represented as a
partially ordered, labeled XML tree. This imposes a
great challenge on data management systems which
have traditionally been designed to cope with struc-
tured rather than semistructured data. In recent years,
a lot of work has thus been done to develop new meth-
ods for storing and querying XML data using XML
query languages, such as XPath (W3C, 2006b) and
XQuery (W3C, 2006c).
At the heart of the XPath query language, there are
12 axes, i.e., operators for tree traversal. In this paper,
we present a method for accelerating the evaluation
of the major axes, i.e., the ancestor, descendant,
preceding, and following axes, through partition-
ing. We make use of the observation that starting
from any node, the main axes partition the document
into four disjoint partitions. Our idea is to partition
the nodes more accurately, store the partition infor-
mation, and use this information to filter the nodes
that cannot be contained in the result before actually
performing the axis.
Since our method is based on simple geometric
properties of the preorder and postorder numbers of
the nodes, it is somewhat similar to the XML index-
ing approaches based on spatial structures, such as R-
trees (Grust, 2002) or UB-trees (Kr
´
atk
´
y et al., 2004).
The method described in this paper, however, is very
easy to implement even using B-trees, and thus it can
easily be used to accelerate XPath evaluation in XML
management systems built on relational databases,
such as XRel (Yoshikawa et al., 2001) and XPath ac-
celerator (Grust, 2002). Furthermore, our approach
can also be tailored to be used with other node identi-
fication schemes, such as the order/size scheme.
The rest of our paper is organized as follows. In
section 2, we take a short look at the related work and
in section 3, we present our own partitioning method.
In section 4, we discuss the implementation of our
method and in section 5, the results of our experimen-
tal evaluation. Section 6 concludes this article and
discusses our future work.
2 RELATED WORK
In the XML research literature, there are numerous
examples of different XML management systems.
96
Luoma O. (2007).
ACCELERATING XPATH AXES THROUGH STRUCTURAL PARTITIONING.
In Proceedings of the Third International Conference on Web Information Systems and Technologies - Internet Technology, pages 96-103
DOI: 10.5220/0001283800960103
Copyright
c
SciTePress

These systems can roughly be categorized into the fol-
lowing three categories:
• The flat streams approach handles the documents
as byte streams (Peng & Chawathe, 2003) (Barton
et al., 2003). Obviously, accessing the structure
of the documents requires parsing and consumes
a lot of time, but this option might still be viable
in a setting where the documents to be stored and
queried are small.
• In the metamodeling approach, the XML doc-
uments are first represented as trees which are
then stored into a database. With suitable in-
dexes this approach provides fast access to sub-
trees, and thus the metamodeling approach is by
far the most popular in the field of XML man-
agement research. Unlike in the flat streams ap-
proach, however, rebuilding large parts of origi-
nal documents from a large number of individual
nodes can be rather expensive. The partitioning
method discussed in this paper also falls into this
category.
• The mixed approach aims at combining the previ-
ous two approaches. In some systems, the data is
stored in two redundant repositories, one flat and
one metamodeled, which allows the stored doc-
uments to be queried and the result documents
to be built efficiently, but obviously creates some
storage overhead. This problem could be tackled
by compression to which XML data is often very
amenable. There are also examples of a hybrid
approach in which coarser structures of the XML
documents are modeled as trees and finer struc-
tures as flat streams (Fiebig et al., 2003).
A lot of work has been carried out to accelerate
structural joins (Al-Khalifa et al, 2002), i.e., opera-
tions which determine all occurrences of parent/child,
ancestor/descendant, preceding/following etc. rela-
tionships between node sets. Some approaches are
based on indexes built on XML trees, whereas oth-
ers aim at designing more efficient join algorithms.
The former category includes the so called proxy in-
dex (Luoma, 2005b) (Luoma, 2006) which effectively
partitions the nodes into overlapping partitions so that
the ancestors of any given node are contained within
the same partition. Thus, when the ancestors of a
given node are retrieved it is sufficient to check the
partitions to which the node is assigned. Conversely,
descendants can also be found efficiently since there
is no need to check the partitions to which the node
is not assigned. However, this approach is suitable
for accelerating only ancestor/descendant operations.
The method discussed in this paper, on the contrary,
can also accelerate preceding/following operations.
The other group of methods include, for example,
the staircase join (Grust & van Keulen, 2003). The
idea of the staircase join is to prune the set of con-
text nodes, i.e., the initial nodes from which the axis
is performed. For instance, for any two context nodes
n and m such that m is a descendant of n, all descen-
dants m are also descendants of n, and thus m can be
pruned before evaluating the descendant axis. An-
other method based on preprocessing the nodes was
proposed in (Tang et al., 2005). In this approach
the nodes were partitioned somewhat similarly to the
method discussed in this paper. However, both of
these methods require a considerable amount of pro-
gramming effort since they work by preprocessing the
data rather than by building indexes. In the context of
relational databases, for example, this would mean ei-
ther reprogramming the DBMS internals or program-
ming a collection of external classes to implement
the join algorithms. Our method, on the contrary, re-
quires very little programming effort even when im-
plemented using a relational database, which we re-
gard as the main advantage of our approach.
3 XPATH BASICS
As mentioned earlier, XPath (W3C, 2006b) is based
on a tree representation of a well-formed XML docu-
ment, i.e., a document that conforms to the syntactic
rules of XML. A simple example of an XML tree cor-
responding to the XML document <b><c d="y"/><c
d="y"><e>kl </e></c><c><e>ez</e></c></b> is
presented in Figure 1. The nodes are identified using
their preorder and postorder numbers which encode a
lot of structural information
1
.
The tree traversals in XPath are based on 12 axes
which are presented in Table 1. In simple terms, an
XPath query can be thought of as a series of location
steps of the form /axis::nodetest[predicate]
which start from a context node - initially the root of
the tree - and select a set of related nodes specified by
the axis. A node test can be used to restrict the name
or the type of the selected nodes. An additional predi-
cate can be used to filter the resulting node set further.
The location step n/child::c[child::*], for ex-
ample, selects all children of the context node n which
are named ”c” and have one or more child nodes. As
a shorthand for axes child, descendant-or-self,
and attribute, one can use /, //, and /@, respec-
tively.
1
In preorder traversal, a node is visited before its sub-
trees are recursively traversed from left to right and in pos-
torder traversal, a node is visited after its subtrees have been
recursively traversed from left to right.
ACCELERATING XPATH AXES THROUGH STRUCTURAL PARTITIONING
97

1
,
10
b
2
,2
c
4,6
c
8,9
c
9,8
e
6,5
e
5,3
@d=”y”
3
,1
@d=”y”
7,4
”kl”
1
0,7
”ez”
Element node
Attribute node
Text node
Figure 1: An XML tree.
Table 1: XPath axes and their semantics.
Axis Semantics of n/Axis
parent Parent of n.
child Children of n, no attribute nodes.
ancestor Transitive closure of parent.
descendant Transitive closure of child, no attribute nodes.
ancestor-or-self Like ancestor, plus n.
descendant-or-self Like descendant, plus n, no attribute nodes.
preceding Nodes preceding n, no ancestors or attribute nodes.
following Nodes following n, no descendants or attribute nodes.
preceding-sibling Preceding siblings of n, no attribute nodes.
following-sibling Following siblings of n, no attribute nodes.
attribute Attribute nodes of n.
self Node n.
Using XPath, it is also possible to set con-
ditions for the string values of the nodes. The
XPath query //record="John Scofield Groove
Elation Blue Note", for instance, selects all ele-
ment nodes with label ”record” for which the value
of all text node descendants concatenated in doc-
ument order matches ”John Scofield Groove Ela-
tion Blue Note”. Notice also that the result of
an XPath query is the concatenation of the parts
of the document corresponding to the result nodes.
In our example case, query //c//*, for exam-
ple, would result in no less than <c d="y"/><c
d="y"><e>kl</e></c><c><e>ez</e></c>
<e>kl </e><e>ez</e>.
4 PARTITIONING METHOD
As mentioned earlier, we rely on pre-/postorder en-
coding (Dietz, 1982), i.e., we assign both preorder
and postorder numbers for the nodes. This encoding
provides us with enough information to evaluate the
four major axes (Grust, 2002) as follows
2
:
Proposition 1. Let pre(n) and post(n) denote the pre-
order and postorder numbers of node n, respectively.
For any two nodes n and m, n ∈ m/ancestor::*
iff pre(n) < pre(m) and post(n) > post(m),
n ∈ m/descendant::* iff pre(n) > pre(m) and
post(n) < post(m), n ∈ m/preceding::* iff
pre(n) < pre(m) and post(n) < post(m), and
n ∈ m/following::* iff pre(n) > pre(m) and
post(n) > post(m).
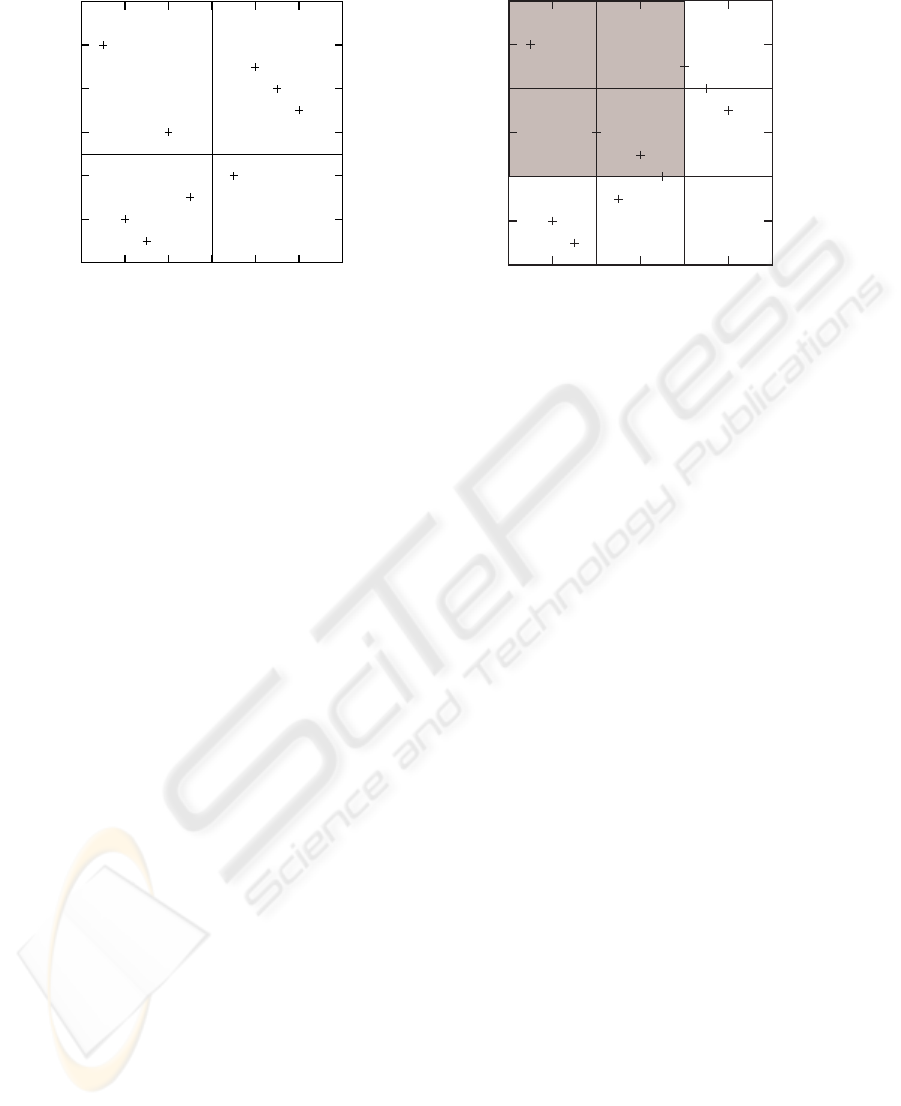
This observation is exemplified on the left side of
Figure 2 which shows the partitioning created by the
major axes using node (6,5) as the context node. The
ancestors of node (6,5) can be found in the upper-left
partition, the descendants in the lower-right partition,
2
This is actually a bit inaccurate since the attribute
nodes, for example, are not in the result of the descendant
axis. However, if all nodes are treated equally, the proposi-
tion holds.
WEBIST 2007 - International Conference on Web Information Systems and Technologies
98
0
2
4
6
8
10
12
0 2 4 6 8 10 12
Post
Pre
0
2
4
6
8
10
12
0 2 4 6 8 10 12
Post
Pre
Figure 2: Examples on the major axes (left) and partitioning using value 4 for p (right).
the predecessors in the lower-left partition, and the
followers in the upper-right partition. Based on the
previous observation, the following proposition is ob-
vious:
Proposition 2. For any two nodes n and m and
for any p > 0, bpre(n)/pc ≤ bpre(m)/pc and
bpost(n)/pc ≥ bpost(m)/pc if n ∈ m/ancestor::*,
bpre(n)/pc ≥ bpre(m)/pc and bpost(n)/pc ≤
bpost(m)/pc if n ∈ m/descendant::*,
bpre(n)/pc ≤ bpre(m)/pc and bpost(n)/pc ≤
bpost(m)/pc if n ∈ m/preceding::*, and
bpre(n)/pc ≥ bpre(m)/pc and bpost(n)/pc ≥
bpost(m)/pc if n ∈ m/following::*.
Proposition 2 provides us with simple means for
partitioning the nodes into disjoint subsets. The parti-
tioning is exemplified in Figure 2 (right) which shows
the nodes of our example tree partitioned using value
4 for p. It should now be obvious that when searching,
for instance, the ancestors of node (6,5), it is sufficient
to check the nodes in the shaded partitions since other
partitions cannot contain any ancestors. In what fol-
lows, values bpre(n)/pc and bpre(n)/pc where n is a
node residing in partition P are simply referred to as
the preorder and postorder number of P and denoted
by pre(P) and post(P), respectively.
Many minor axes can also benefit from
partitioning. The ancestor-or-self and
descendant-or-self axes, for example, behave
similarly to ancestor and descendant axes, and
thus they can be accelerated using the same partition
information. The results of preceding-sibling
and following-sibling, on the other hand, are
subsets of preceding and following and the results
of parent and child subsets of ancestor and
descendant so they can also be accelerated using
the partitioning. However, other minor axes than
ancestor-or-self and descendant-or-self
are generally very easy to evaluate, and thus using
the partition information to evaluate them is often
just unnecessary overhead especially if we have an
index which can be used to locate the nodes with a
given parent node efficiently (Luoma, 2005a). One
should also notice that in practice, the nodes are
not distributed evenly and there are several empty
partitions. Thus, the number of non-empty partitions
is usually much smaller than p
2
.
5 IMPLEMENTATION OPTIONS
5.1 Relational Implementation
To test our idea, we designed a relational database
according to the principles described in the previous
section. As the basis of our implementation, we chose
the XPath accelerator (Grust, 2002). In order to store
the partition information, we employed relation Part,
and thus we ended up with the following relational
schema:
Node(Pre, Post, Par, Part, Type, Name, Value)
Part(Part, Pre, Post)
As in the original proposal, the database attributes
Pre, Post, Par, Type, Name, and Value of the Node
relation correspond to the pre- and postorder num-
bers, the preorder number of the parent, the type, the
name, and the string value of the node, respectively.
The database attributes Type, Name, and Value are
needed to support node tests and string value tests; the
axes can be evaluated using database attributes Pre,
ACCELERATING XPATH AXES THROUGH STRUCTURAL PARTITIONING
99

Post, and Par. The partition information is contained
in the Part table in which the database attributes Pre
and Post correspond to the preorder and postorder
number of the partition, respectively. The database
attribute Part in the Node relation is a foreign key
referencing to the primary key of the Part relation.
For the sake of brevity, we do not describe the
XPath-to-SQL query translation in detail; the de-
tails can be found in (Yoshikawa et al., 2001) and
(Grust, 2002). For our purposes, it is sufficient to
say that in order to perform structural joins, these
systems issue SQL queries which involve nonequi-
joins, i.e., joins using < or > as the join condition,
which can easily lead to scalability problems (Luo-
ma, 2006). In XPath accelerator, the XPath query
n
0
/descendant::*, for instance, is transformed into
the following SQL query:
SELECT DISTINCT n
1
.*
FROM Node n
0
, Node n
1
WHERE n
1
.Pre>n
0
.Pre AND n
1
.Post<n
0
.Post
ORDER BY n
1
.Pre;
Notice that tuple variables n
0
and n
1
are joined
completely using slow nonequijoins. However, we
can use the partition information stored into table
Part to replace some of the nonequijoins with much
faster equijoins, i.e., joins using = as the join condi-
tion. With the partition information, the same query
can be evaluated much more efficiently using the fol-
lowing piece of SQL:
SELECT DISTINCT n
1
.*
FROM Node n
0
, Node n
1
, Part a
1
, Part b
1
WHERE a
1
.Part=n
0
.Part AND b
1
.Pre>=a
1
.Pre
AND b
1
.Post<=a
1
.Post AND n
1
.Part=b
1
.Part AND
n
1
.Pre>n
0
.Pre AND n
1
.Post<n
0
.Post
ORDER BY n
1
.Pre;
In simple terms, we use tuple variable a
1
for
the partition in which node corresponding to tu-
ple variable n
0
resides. Variable b
1
corresponds
to the partitions which can contain descendants of
n
0
; condition n
1
.Part=b
1
.Part restricts our search
into the nodes residing in those partitions. Fi-
nally, we simply use condition n
1
.Pre>n
0
.Pre AND
n
1
.Post<n
0
.Post to retrieve the actual descendants.
The nonequijoins on the Part table are seldom a
problem since the Part table is rather small provided
that p, i.e., the number of partitions, has been selected
carefully. Other major axes can obviously be acceler-
ated similarly.
5.2 Native Implementation
We also implemented a simple XPath processor
which parses an XML document and splits the nodes
corresponding to the document into partitions which
are maintained in the main memory. For each node,
our system maintains its preorder number, postorder
number, reference to its parent, type, name, and string
value. In other words, the representation of the nodes
is similar to the relational implementation discussed
earlier. The partitions are lexically sorted according to
their pre- and postorder numbers and the nodes within
the partitions are sorted in preorder. Thus, given
node n, set of partitions S, and axis axis, the follow-
ing join algorithm simply iterates the partitions and
checks only the partitions which can contain nodes in
n/axis::*. For the sake of brevity, we do not treat all
axes in algorithm join; operator + is used as a short-
hand for operation which adds an item to a set and
par(n) denotes the parent of node n.
join(n, S, axis, p)
in: Node n, partition set S, XPath axis axis, partitioning
factor p
out: Nodes in n/axis::* in S
if axis = preceding or axis = preceding-sibling
for each P ∈ S
if pre(P) ≤ bpre(n)/pc and post(P) ≤ bpre(n)/pc
result ← result + joinPart(n, P, axis)
...
return result
The structural joins within a partition, then, are
carried out using algorithm joinPart:
joinPart(n, P, axis)
in: Node n, partition P, XPath axis axis
out: Nodes in n/axis::* of p
if axis = preceding then
for each m ∈ M
if pre(m) < pre(n) and post(m) < post(n)
result ← result + m
if axis = preceding-sibling then
for each m ∈ M
if pre(m) < pre(n) and par(m) = par(n)
result ← result + m
...
return result
Again, our algorithm is heavily simplified. How-
ever, it is easy to extend the algorithm to support
node tests and string value tests by checking the type,
name, and string value attributes of the node. No-
tice also that we could dramatically lower the number
WEBIST 2007 - International Conference on Web Information Systems and Technologies
100

of structural joins by considering the fact that the all
nodes in partition P such that pre(P) < bpre(n)/pc
and post(P) < bpost(n)/pc are guaranteed to be in
n/preceding::*, and thus they could be added to the
result without performing the structural joins. We also
implemented this option but found out that is did not
lead to considerable gains in evaluation times. How-
ever, the benefits obviously depend on the implemen-
tation and in some cases, this approach can further
accelerate the joins.
6 EXPERIMENTAL RESULTS
6.1 Relational Implementation
We implemented the relational option using Win-
dows XP and Microsoft SQL Server 2000 running
on 2.00 GHz Pentium PC Equipped with 512 MB
of RAM and standard IDE disks. The algorithms
needed to build the databases, as well as the algo-
rithms for query translation, were implemented using
Java. We built indexes on Node(Post), Node(Name),
Part(Pre), and Part(Post) and a clustered index
on Node(Part). As our test data sets, we used the
1998 baseball statistics (52707 nodes) and the col-
lection of Shakespeare’s plays (327129 nodes), both
available at http://www.ibiblio.org/examples.
The sizes of these documents were 640 kB and 7.47
MB, respectively; values 1, 2, 4, ..., 256 were used as
a partitioning factor p.
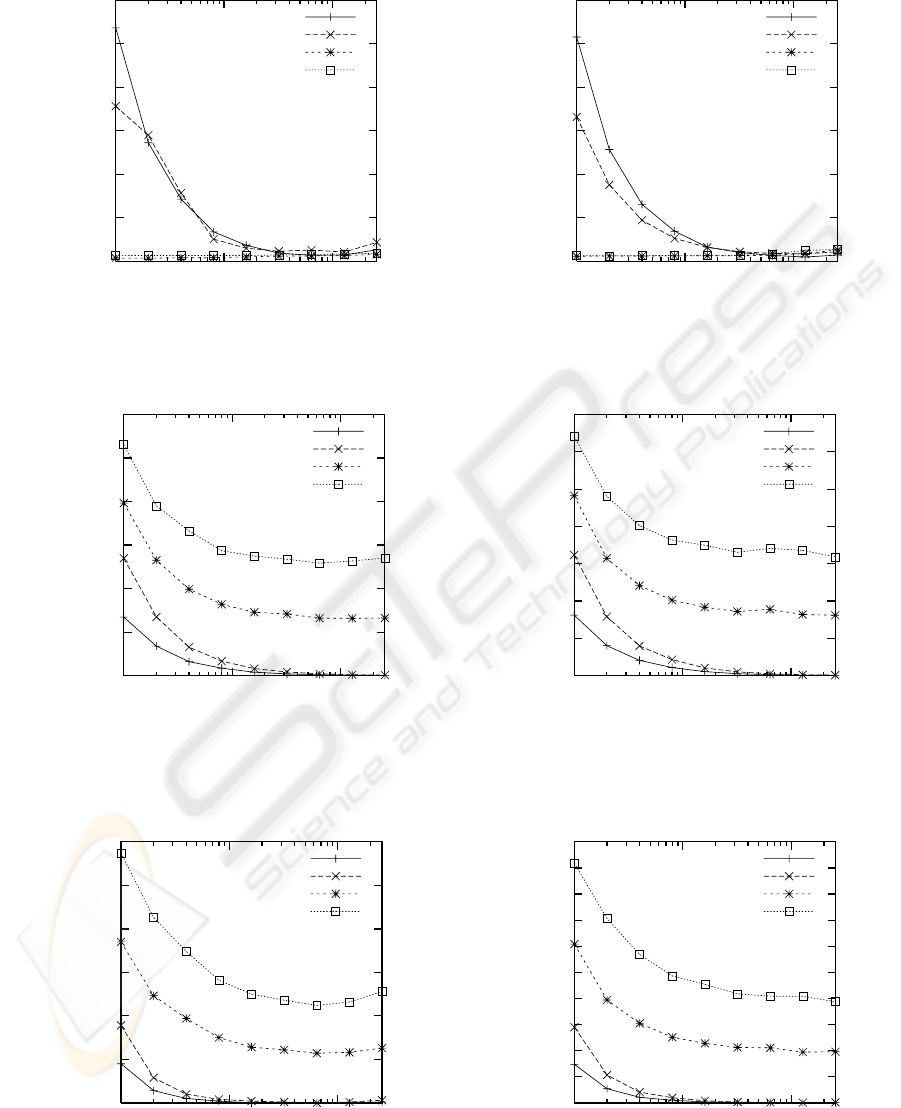
Figure 3 presents the query performance for the
major axes using a relatively large set of context
nodes; in these figures, the word ”Partitions” refers
to the value of p or the number of partitions per (pre-
order or postorder) dimension. In the case of base-
ball.xml, nodes with name ”PLAYER” (1226 nodes)
and in plays.xml, nodes with name ”SCENE” (750
nodes) served as the context nodes. One should no-
tice that our method can lead to considerable perfor-
mance gains in ancestor and descendant axes even
with a very small amount of partitions. In the case
baseball.xml and 16 partitions per dimension, for ex-
ample, there were only 55 partitions in total. Thus,
there were only 55 rows in the Part table, which is
certainly acceptable considering that there are no less
than 52707 nodes in the Node table. Even in the case
of 256 partitions per dimension, there were only 772
rows in the Part table for ”1998statistics.xml” and
859 rows for ”plays.xml”.
In the case of preceding and following axes,
however, no real acceleration could be observed.
These axes could be actually evaluated very effi-
ciently even without the partitionin, which is due to
the very sophisticated join algorithms implemented
in SQL Server. Nevertheless, considering that the
ancestor and descendant axes were very time-
consuming to evaluate without the partition informa-
tion, we are still convinced that the small amount of
partition information can indeed pull its weight.
6.2 Native Implementation
The evaluation of our native implementation was car-
ried out using the same equipment and data sets which
were used in the relational case. Furthermore, the
same number of partitions per dimension were used
but in these tests, we randomly selected the context
nodes. Figures 4 and 5 present the results obtained
using the native implementation; all results are aver-
ages for 100 iterations. Overall, the ancestor and
descendant axes behaved similarly to the relational
case, i.e., they were considerably accelerated. How-
ever, the preceding and following axes were also
accelerated by roughly a factor of two. This is actu-
ally intuitively clear since an average node has much
more predecessors and followers than it has ances-
tors and descendants, and thus the preceding and
following axes usually result in much larger node
sets. In the case of ancestor axis, for example, the
partitioning can help us to filter out a massive amount
of nodes, i.e., the most of the descendants, predeces-
sors, and followers, whereas in the case of preceding
axis, a much smaller amount of nodes with respect to
the size of the result can be filtered.
One should also notice that ordering the nodes
according to their preorder numbers favors the
preceding axis over the following axis. After the
preorder numbers have been checked in the case of
preceding axis, we still have to filter out the ances-
tors using the postorder numbers of the nodes. In
the case of following axis, on the contrary, the de-
scendants have to be filtered, which is a harder task
since a node in an XML tree usually has more de-
scendants than it has ancestors. Conversely, sorting
the nodes according to their postorder numbers favors
the following axis.
7 CONCLUDING REMARKS
In this paper, we discussed a partitioning method
which can considerably accelerate the evaluation of
XPath axes in different XML management systems.
Our method is based on simple properties of the pre-
order and postorder numbers of the nodes in an XML
tree, which makes it very easy to implement. This
was exemplified by presenting two different imple-
ACCELERATING XPATH AXES THROUGH STRUCTURAL PARTITIONING
101
0
5000
10000
15000
20000
25000
30000
1 10 100
Time (ms)
Partitions
ancestor
descendant
preceding
following
0
20000
40000
60000
80000
100000
120000
1 10 100
Time (ms)
Partitions
ancestor
descendant
preceding
following
Figure 3: Relational results 1998statistics.xml (left) and plays.xml (right).
0
20000
40000
60000
80000
100000
120000
1 10 100
Joins
Partitions
ancestor
descendant
preceding
following
0
100000
200000
300000
400000
500000
600000
700000
1 10 100
Joins
Partitions
ancestor
descendant
preceding
following
Figure 4: Number of joins for the major axes using random context nodes for 1998statistics.xml (left) and plays.xml (right);
native implementation.
0
50
100
150
200
250
300
1 10 100
Time (ms)
Partitions
ancestor
descendant
preceding
following
0
200
400
600
800
1000
1200
1400
1600
1800
2000
1 10 100
Time (ms)
Partitions
ancestor
descendant
preceding
following
Figure 5: Times for the major axes using random context nodes for 1998statistics.xml (left) and plays.xml (right); native
implementation.
WEBIST 2007 - International Conference on Web Information Systems and Technologies
102

mentations of our idea which both indicated that our
approach can lead to considerable performance gains.
REFERENCES
Al-Khalifa, S., Jagadish, H. V., Patel, J. M., Wu, Y., Koudas,
N., & Srivastava, D. (2002). In Proceedings of the
18th International Conference on Data Engineering,
(pp. 141-152).
Barton, C., Charles, P., Goyal, D., Raghavachari, M., Fon-
toura, M., & Josifovski, V. (2003). Streaming XPath
processing with forward and backward axes. In Pro-
ceedings of the 19th International Conference on Data
Engineering, (pp. 455-466).
Dietz, P. F. (1982). Maintaining order in a linked list. In
Proceedings of the 14th Annual Symposium on Theory
of Computing, (pp. 122-127).
Fiebig, T., Helmer, S., Kanne, C-C., Moerkotte, G., Neu-
mann, J., Schiele, R., & Westmann, T. (2003). Natix:
A technology overview. In Web, Web-Services, and
Database Systems, NODe 2002 Web and Database-
Related Workshops, (pp. 12-33).
Grust, T. (2002). Accelerating XPath location steps. In Pro-
ceedings of the 2002 ACM SIGMOD Conference on
Management of Data, (pp. 109-120).
Grust, T., & van Keulen, M. (2003). Tree awareness for re-
lational RDBMS kernels: Staircase join. In Intelligent
Search on XML Data, Applications, Languages, Mod-
els, Implementations, and Benchmarks, (pp. 231-245).
Kr
´
atk
´
y, M., Pokorn
´
y, J., & Sn
´
a
ˇ
sel, V. (2004) Implementa-
tion of XPath axes in the multi-dimensional approach
to indexing XML data. In Proceedings of Current
Trends in Database Technology, (pp. 219-229).
Luoma, O. (2005). Modeling nested relationships in XML
documents using relational databases. In Proceedings
of the 31st Conference on Current Trends in Theory
and Practice of Computer Science, (pp. 259-268).
Luoma, O. (2005). Supporting XPath axes with relational
databases using a proxy index. In Proceedings of the
3rd International XML Database Symposium, (pp. 99-
113).
Luoma, O. (2006). Xeek: An efficient method for support-
ing XPath evaluation with relational databases. In Lo-
cal Proceedings of the 10th East-European Confer-
ence on Advances in Databases and Information Sys-
tems, (pp. 30-45).
Peng, F., & Chawathe, S. S. (2003). XPath queries on
streaming data. In Proceedings of the 2003 ACM SIG-
MOD Conference on Management of Data, (pp. 431-
442).
Tang, N., Yu, J. X., Wong, K-F., L
¨
u, K., & Li, J. (2005).
Accelerating XML structural join by partitioning. In
Proceedings of the 16th International Conference on
Database and Expert Systems Applications, (pp. 280-
289).
Yoshikawa, M., Amagasa, T., Shimura, T., & Uemura,
S. (2001) XRel: A path-based approach to stor-
age and retrieval of XML documents using relational
databases. ACM Transactions on Internet Technology,
1(1), 110-141.
W3C (World Wide Web Consortium). Ex-
tensible Markup Language (XML) 1.0.
http://www.w3c.org/TR/REC-xml/.
W3C (World Wide Web Consortium). XML path language
(XPath) 2.0. http://www.w3c.org/TR/xpath20/.
W3C (World Wide Web Consortium).
XQuery 1.0: An XML query language.
http://www.w3c.org/TR/xquery/.
ACCELERATING XPATH AXES THROUGH STRUCTURAL PARTITIONING
103
